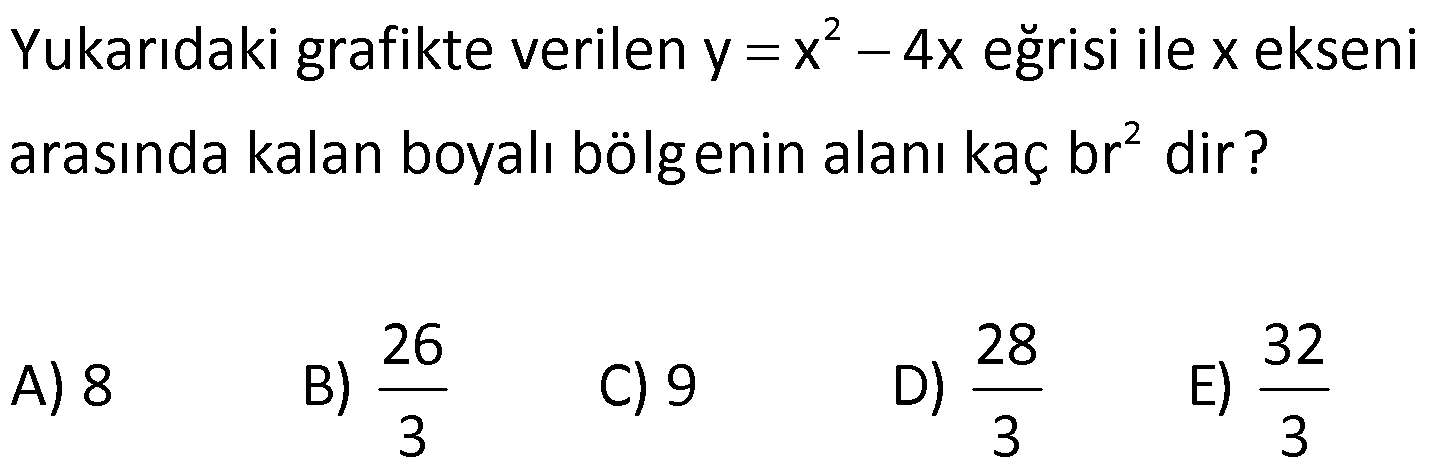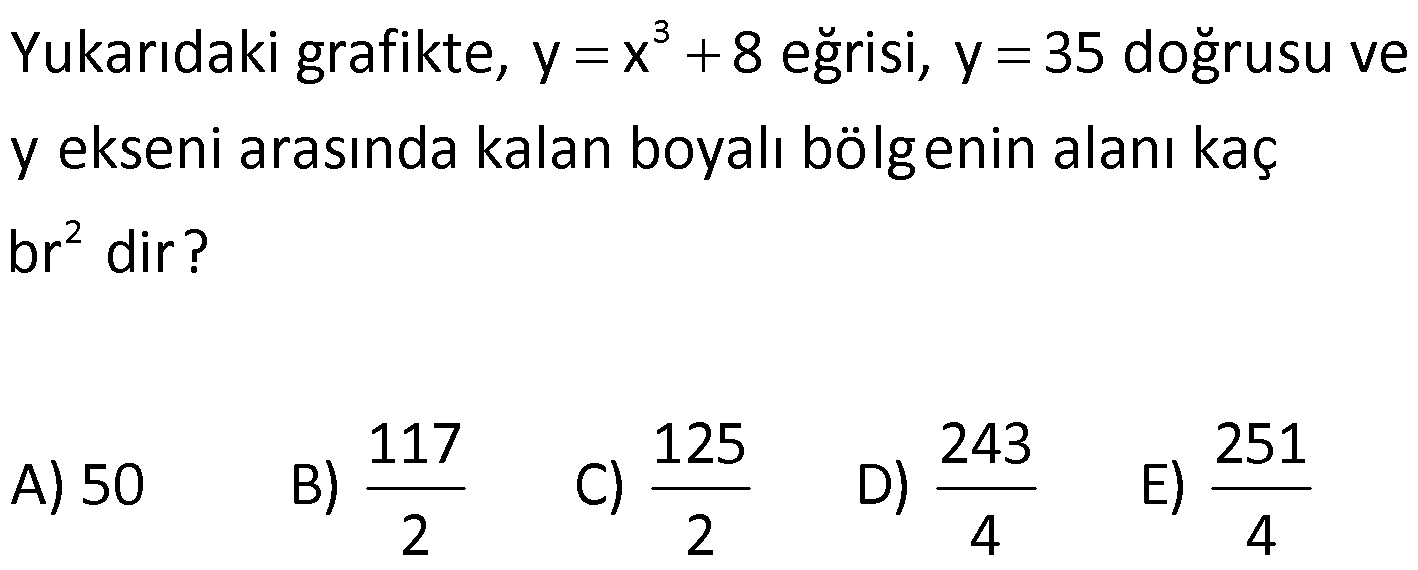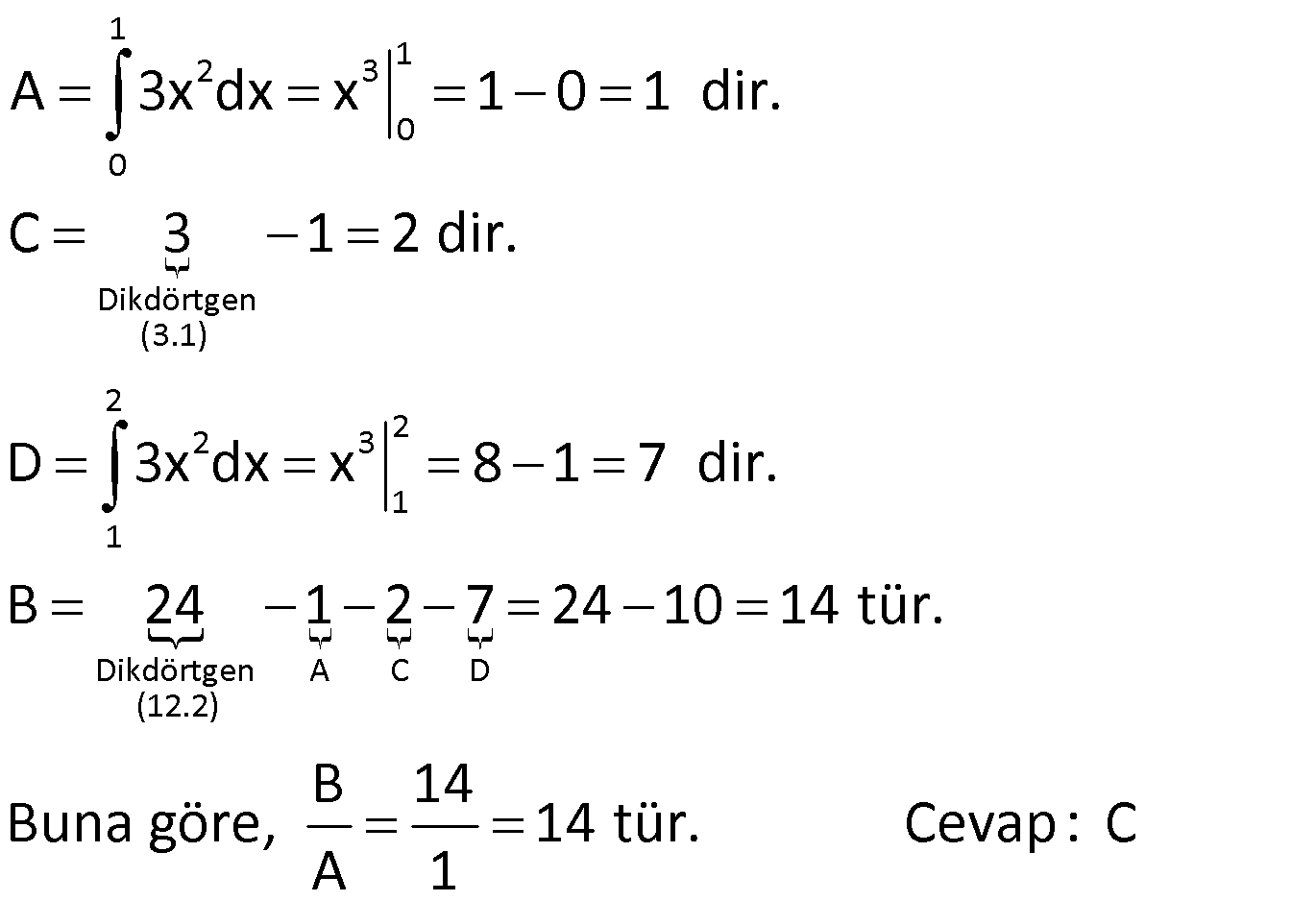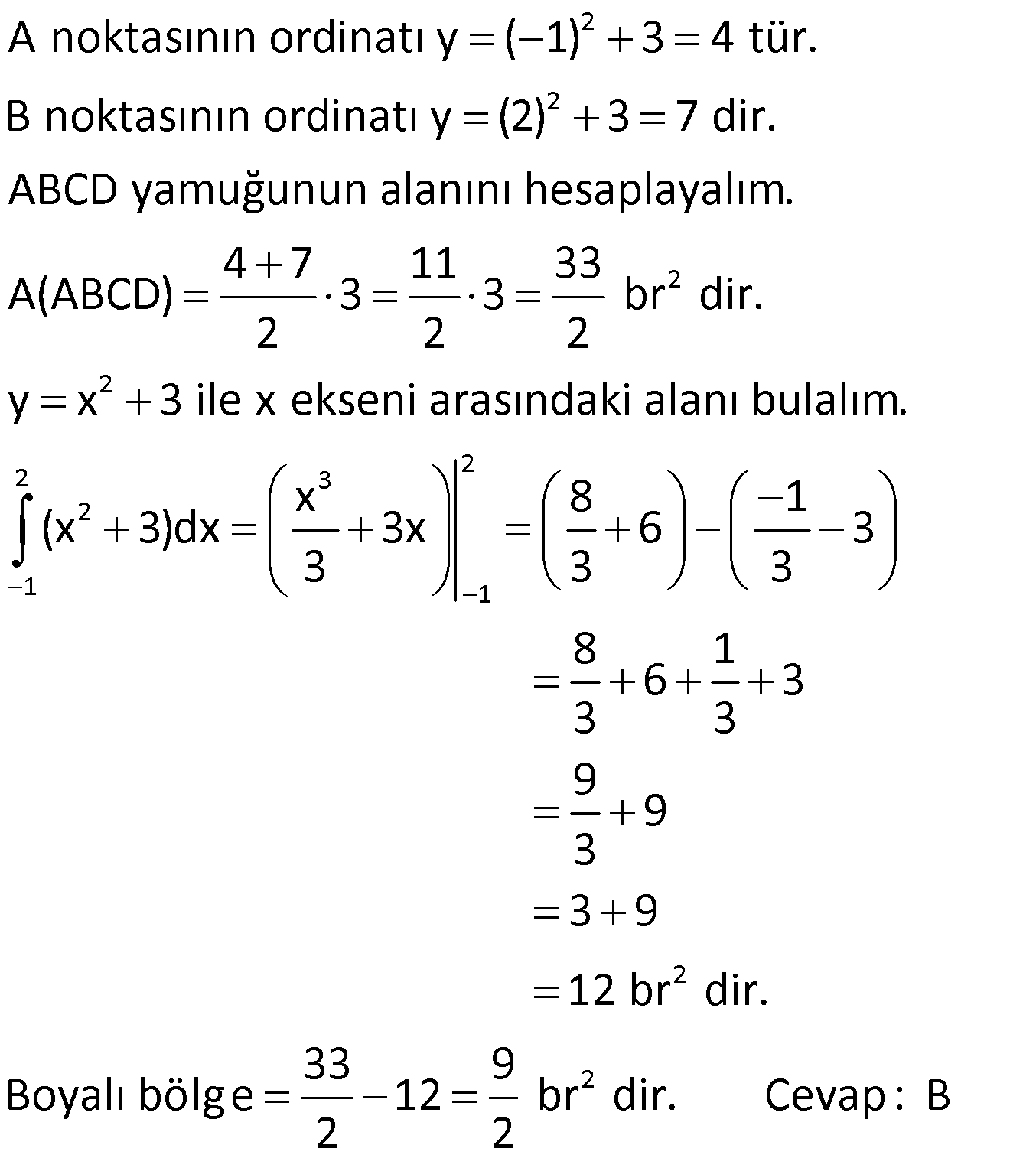Bu bölümde İntegralde Alan ile ilgili 22 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…
Eğer sorular ya da çözümler konusunda bir problem görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.
Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)
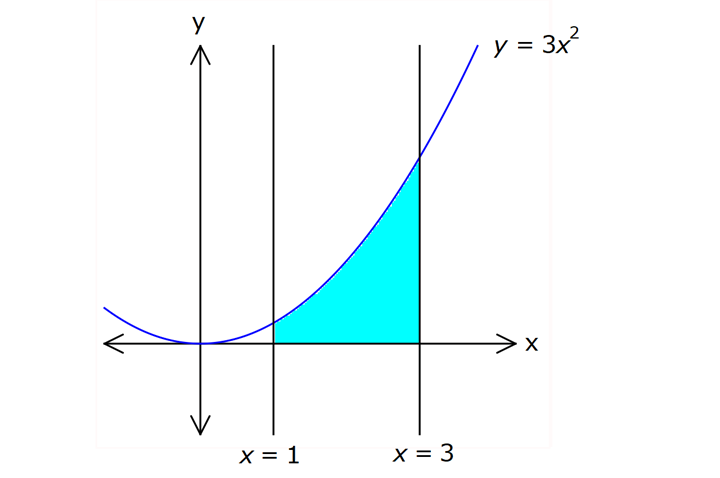
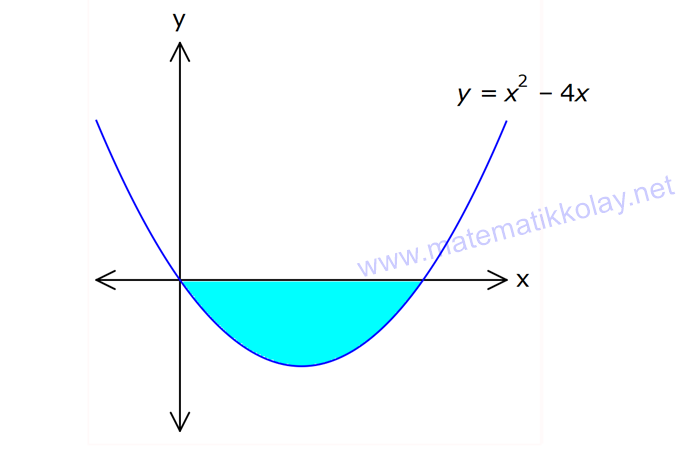
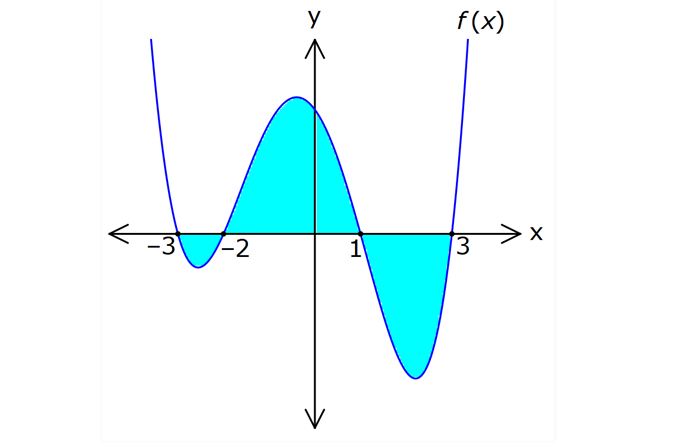
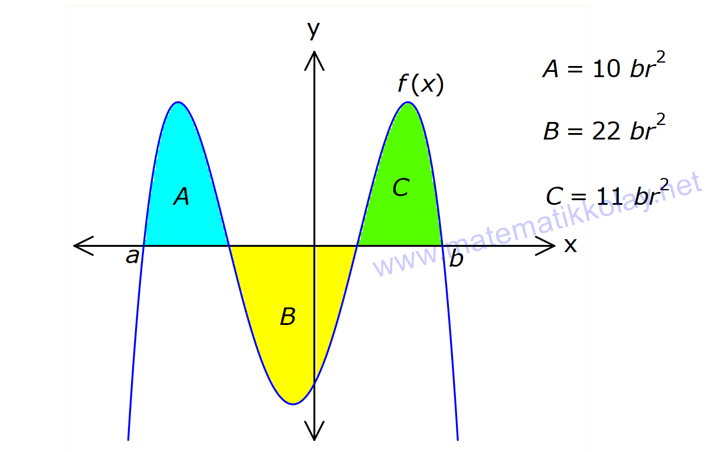
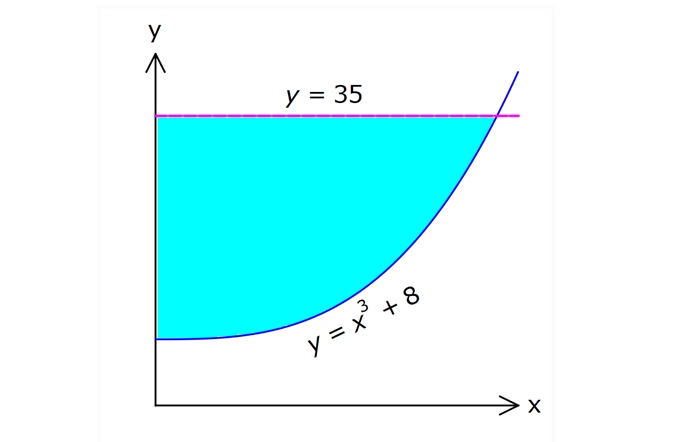
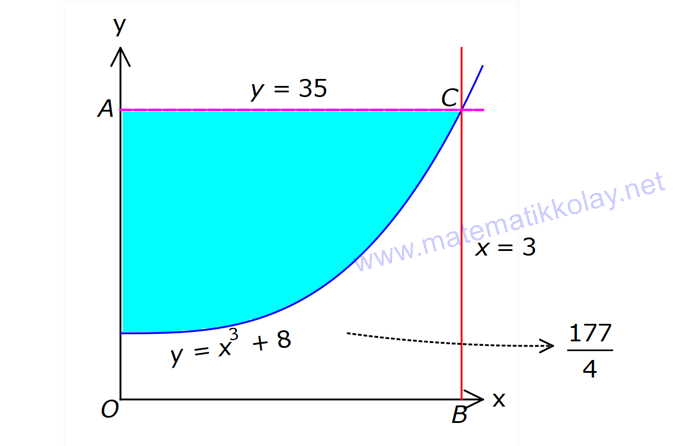
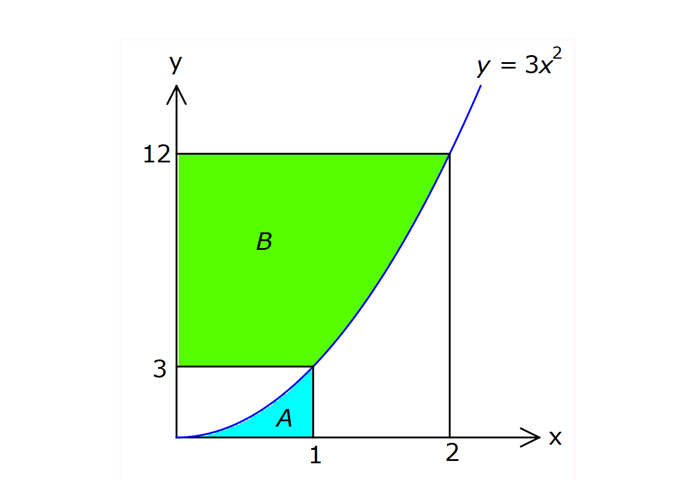
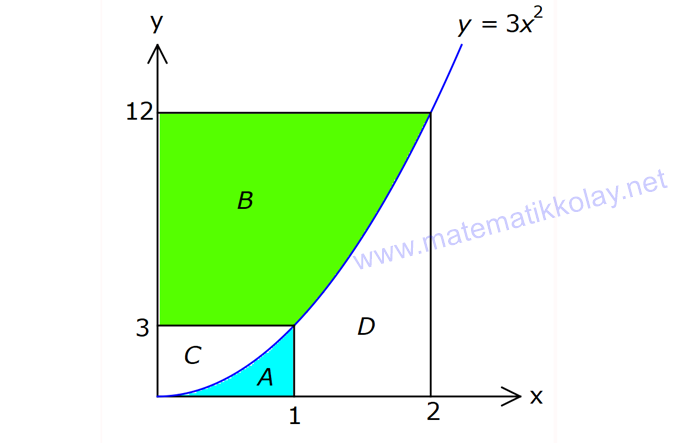
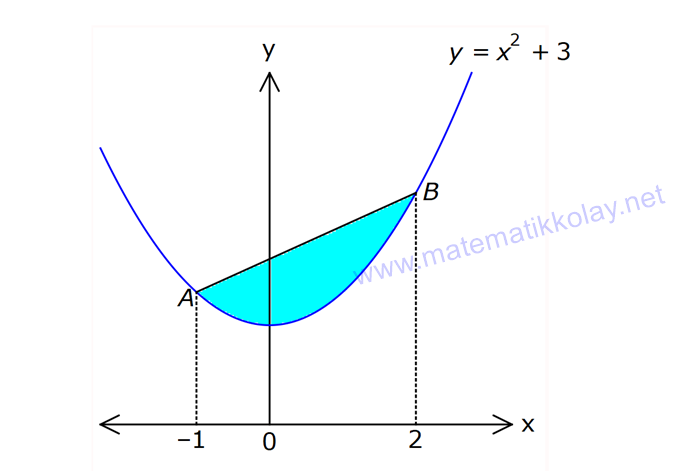
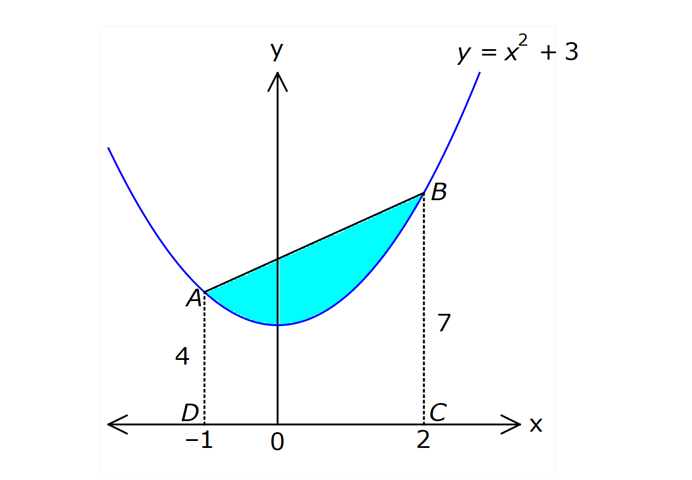
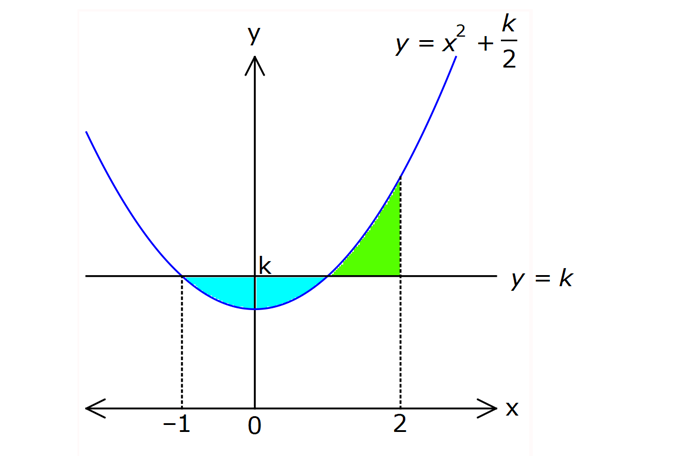
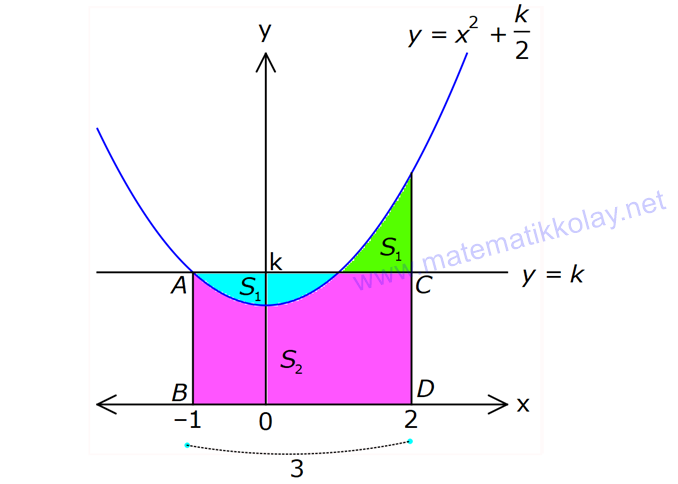
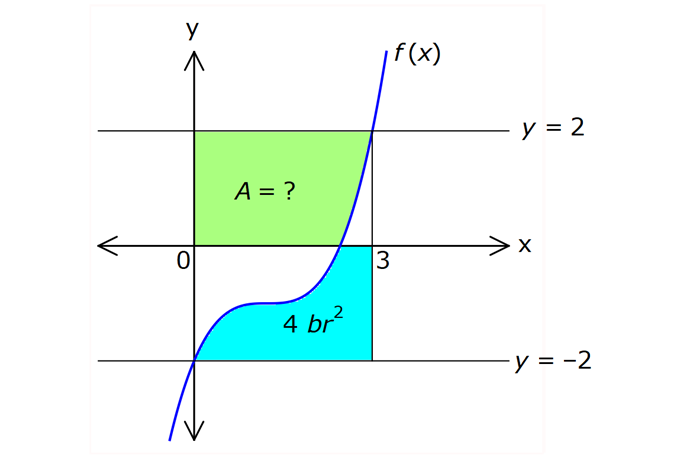
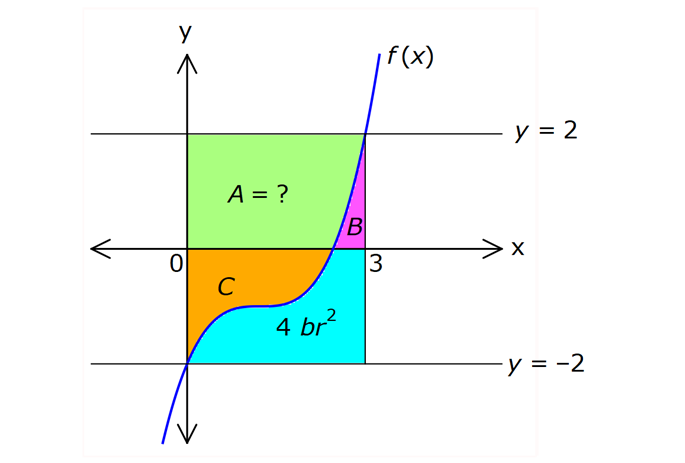
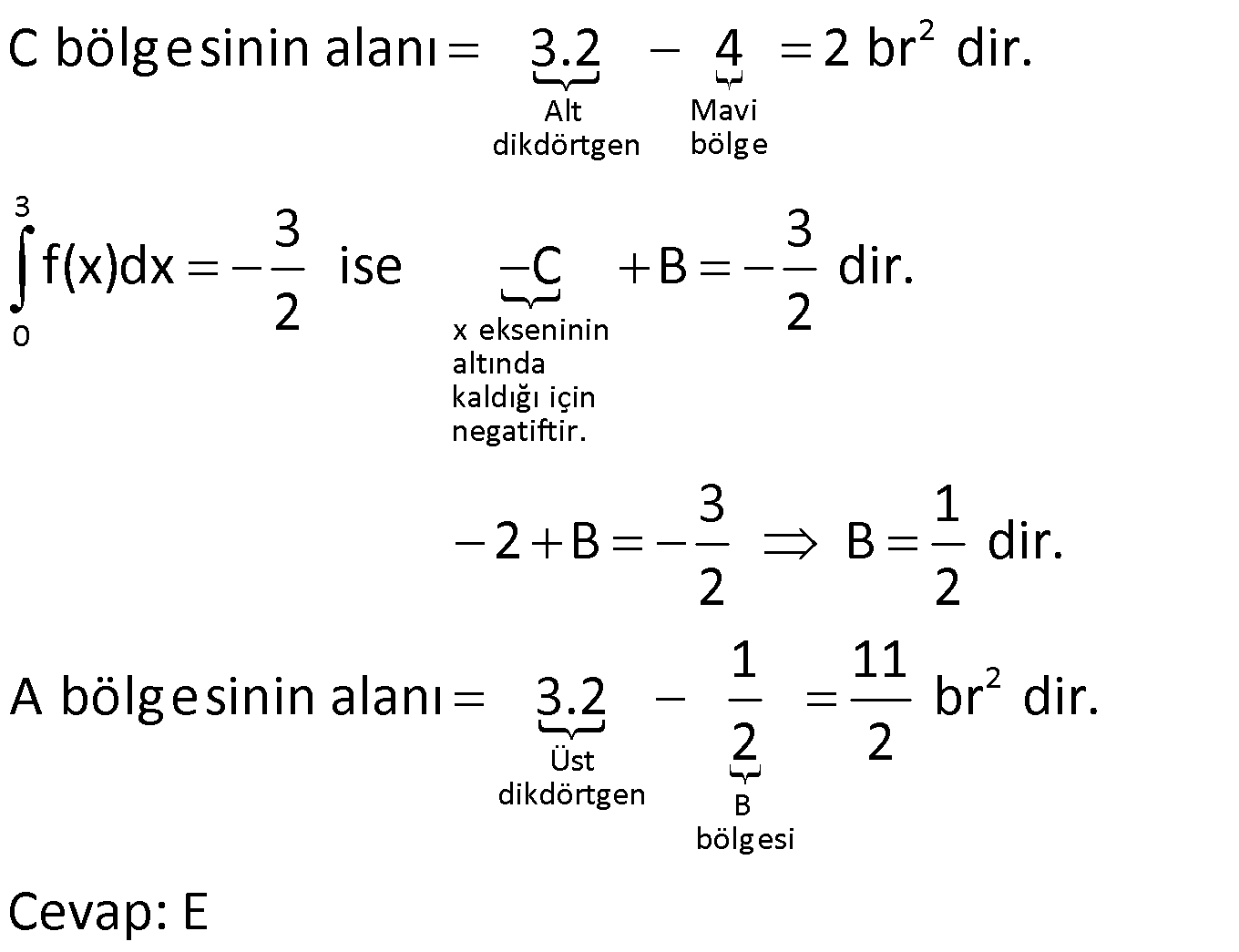
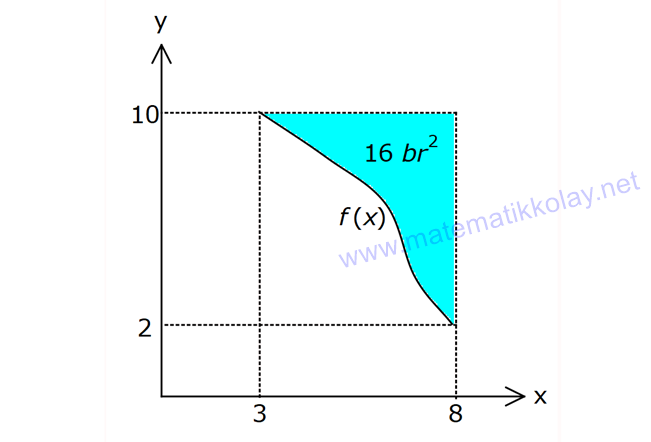
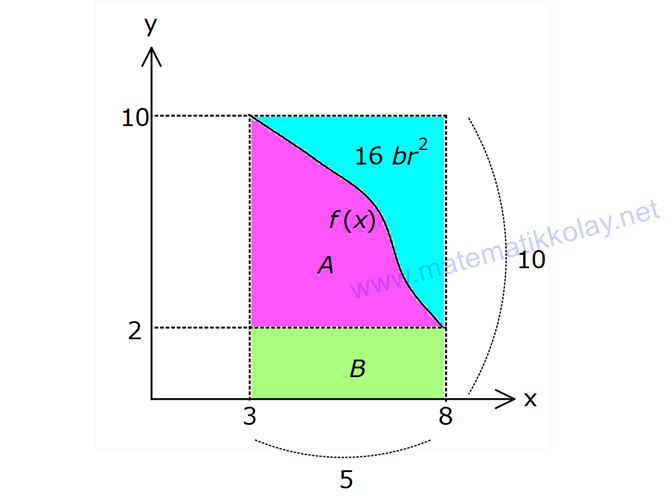
İNTEGRALDE ALAN – 1.KISIM www.matematikkolay.net 1) 2 2 Yukarıdaki grafikte verilen y 3x eğrisi, x 1 ve x 3 doğruları ile x ekseni arasında kalan boyalı bölgenin alanı kaç br dir? A) 26 B) 27 C) 30 D) 32 E) 36 ÇÖZÜM: b a [a, b] kapalı aralığında f(x), integrali alınabilen bir fonksiyon olsun. Bu aralıkta f(x) 0 ise, x a, x b ve x ekseni ile arasındaki kapalı alan f(x)dx Not : 3 3 2 3 1 1 3 3 integrali ile bulunur. Buna göre, Boyalı bölge 3x dx x 3 1 27 1 2 26 br dir. Cevap : A 2) 2 2 Yukarıdaki grafikte verilen y x 4x eğrisi ile x ekseni arasında kalan boyalı bölgenin alanı kaç br dir? 26 28 32 A) 8 B) C) 9 D) E) 3 3 3 ÇÖZÜM: b a [a, b] kapalı aralığında f(x), integrali alınabilen bir fonksiyon olsun. Bu aralıkta f(x) 0 ise, x a, x b ve x ekseni ile arasındaki kapalı alan f(x)dx Not : 2 2 integrali ile bulunur. Yani, x ekseninin altında integral negatif çıktığı için, alan hesabında bunu ile çarpmalıyız. y x 4x eğrisi x ekseni ile nerde kesişir, bulalım. x 4x 0 x(x 4) 0 x 0 ve x 4 4 3 2 2 0 0 4 te keser. Buna göre, x Boyalı bölge (x 4x)dx 2x 3 64 32 0 3 64 32 3 2 64 32 3 32 br dir. 3 Cevap: E www.matematikkolay.net 3) 3 3 2 1 3 3 2 1 Yukarıdaki grafikte verilen y f(x) eğrisi ile x ekseni arasında kalan boyalı bölgenin alanları toplamı aşağıdakilerden hangisi ile ifade edilir? A) f(x)dx B) f(x)dx f(x)dx f(x)dx C) f(x)dx 2 1 3 3 2 1 2 1 3 3 2 1 2 1 3 3 2 1 f(x)dx f(x)dx D) f'(x)dx f'(x)dx f'(x)dx E) f'(x)dx f'(x)dx f'(x)dx ÇÖZÜM: 2 1 3 3 2 1 x ekseninin altında integral negatif çıktığı için, bu bölgelerde integrali ile çarparak, alanı buluruz. x ekseninin üstünde ise bir şey yapmayız. Buna göre, Boyalı alan f(x)dx f(x)dx f(x)dx b a integrali ile bulunur. Cevap: C Mutlak değeri kullanırsak, x a, x b ve x ekseni ile arasındaki kapalı alanı kısaca f(x) dx in Not : tegrali ile ifade edebiliriz. Grafikteki eğri hangi fonksiyona ait ise, bunun integralini alarak, alan hesabını yaparız. Yani, grafik f(x) e ait olduğu için, f'(x) in integralini almayız. Not : 4) b a Yukarıdaki grafikte, y f(x) eğrisi ile x ekseni arasında kalan A, B ve C bölgelerinin alanları verilmiştir. Buna göre, f(x)dx integrali kaça eşittir? A) 1 B) 0 C) 1 D) 23 E) 43 ÇÖZÜM: b a A ve C bölgesinde integral pozitif çıkacağı için, burada alana eşit olurlar. B bölgesinde ise integral negatif çıkacaktır. Bu sebeple alanı ile çarparak kullanmalıyız. O halde, f(x)dx A B C 10 22 11 21 22 1 buluruz. Cevap: A 5) www.matematikkolay.net 3 2 Yukarıdaki grafikte, y x 8 eğrisi, y 35 doğrusu ve y ekseni arasında kalan boyalı bölgenin alanı kaç br dir? 117 125 243 251 A) 50 B) C) D) E) 2 2 4 4 ÇÖZÜM: 3 3 3 3 3 3 0 3 4 0 y 35 ile y x 8 eğrisi nerde kesişir, bulalım. x 8 35 x 27 x 3 te kesişir. y x 8 eğrisinin altındaki alanı (x 8)dx integrali ile bulabiliriz. x 81 81 96 177 8x 24 tür. 4 4 4 4 A(AOBC) 35 2 2 .3 105 br dir. AOBC dikdörtgeninin alanından, integrali çıkarır – sak, boyalı bölgeyi bulabiliriz. 177 420 177 243 Boyalı bölge 105 br dir. 444 Cevap : D 6) 2 Yukarıdaki grafikte y 3x eğrisi ile eksenler arasında oluşturulmuş A ve B bölgeleri gösterilmiştir. Buna göre B alanı, A alanının kaç katıdır? A) 8 B) 12 C) 14 D) 16 E) 20 ÇÖZÜM: 1 1 2 3 0 0 Dikdörtgen (3.1) 2 2 2 3 1 1 Dikdörtgen A C D (12.2) A 3x dx x 1 0 1 dir. C 3 1 2 dir. D 3x dx x 8 1 7 dir. B 24 1 2 7 24 10 14 tür. B 14 Buna göre, 14 tür. Cevap : C A 1 7) www.matematikkolay.net 2 2 Yukarıdaki grafikte y x 3 eğrisi ile [AB] doğru parçası arasında oluşturulmuş boyalı bölgenin alanı kaç br dir? (A ve B noktaları, eğrinin birer noktasıdır.) 3 9 13 15 19 A) B) C) D) E) 2 2 2 2 2 ÇÖZÜM: 2 2 2 2 A noktasının ordinatı y ( 1) 3 4 tür. B noktasının ordinatı y (2) 3 7 dir. ABCD yamuğunun alanını hesaplayalım. 4 7 11 33 A(ABCD) 3 3 br dir. 2 2 2 y x 3 ile x ekseni arasındaki alanı bulalım. 2 2 3 2 1 1 x 8 1 (x 3)dx 3x 6 3 3 3 3 8 1 6 3 3 3 9 9 3 2 2 3 9 12 br dir. 33 9 Boyalı bölge 12 br dir. Cevap : B 2 2 8) www.matematikkolay.net 2 k Yukarıdaki grafikte y x eğrisi ile y k doğrusu 2 arasında oluşan mavi ve yeşil alanların büyüklükleri birbirine eşittir. Buna göre, k reel sayısı kaçtır? A) 1 B) 2 C) 3 D) 4 E) 5 ÇÖZÜM: 2 1 2 2 2 2 1 1 2 2 1 2 3 1 A(ABCD) S S 3.k br dir. k Eğrinin altında kalan alan S S x dx tir. 2 Bu ikisini birbirine eşitleyebiliriz. k 3k x dx 2 x k 3k x 3 2 8 1 k 3k k 3 3 2 8 1 k 3k k 3 3 2 3 3k k 3 2 3k 3 k 2 dir. Cevap :B 2 9) 3 0 2 2 Yukarıdaki grafikte y f(x) eğrisi, y 2, y 2 ve x ekseni arasında çeşitli kapalı alanlar oluşmuştur. 3 f(x)dx dir. 2 Mavi bölgenin alanı 4 br ise, yeşil bölgenin alanı kaç br dir? 7 9 A) B) 4 C) D) 2 2 11 5 E) 2 ÇÖZÜM: www.matematikkolay.net 2 Alt Mavi dikdörtgen bölge 3 0 x ekseninin altında kaldığı için negatiftir. C bölgesinin alanı 3.2 4 2 br dir. 3 3 f(x)dx ise C B dir. 2 2 3 1 2 B B dir. 2 2 A bölg 2 Üst dikdörtgen B bölgesi 1 11 esinin alanı 3.2 br dir. 2 2 Cevap: E 10) 2 3 2 2 Yukarıdaki grafikte y f(x) fonksiyonunun grafiği verilmiştir. Boyalı bölgenin alanı 16 br olduğuna göre, 5x.f(x 1)dx integralinin değeri kaçtır? 68 96 A) B) C) 45 D) 75 E) 85 5 5 ÇÖZÜM: 3 2 2 u 2 2 5x.f(x 1)dx u x 1 olsun. du 2xdx olur. du xdx tir. 2 5du 5xdx olur. 2 Sınır değerleri de ayarlayalım. x 2 için u 2 1 3 tür. x 3 2 3 8 2 2 3 A B alanıdır. dikdörtgen mavi bölge için u 3 1 8 dir. 5 5x.f(x 1)dx f(u) du 2 5 5.10 16 2 5 50 16 2 5 2 34 17 2 85 br dir. Cevap : E
