 Bu bölümde Toplam Fark Formülleri ile ilgili 21 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…
Bu bölümde Toplam Fark Formülleri ile ilgili 21 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…
Eğer sorular ya da çözümler konusunda bir problem görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.
Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)
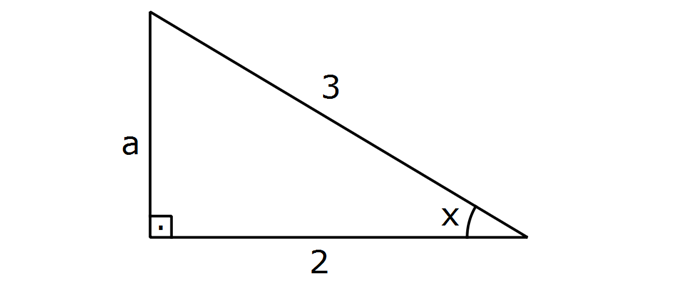
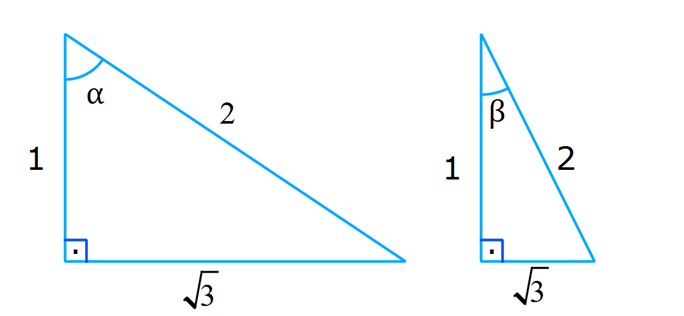
Toplam Fark Formülleri 1) o o o o sin25 cos20 cos25 sin20 ifadesinin değeri kaçtır? 3 1 2 3 A) B) C) D) E) 1 3 2 2 2 Çözüm: o o o o o o o o 5 Toplam Fark Formülleri sin(a b) sina cosb sinb cosa sin a b sina cosb sinb cosa cos a b cosa cosb sina sin sin25 cos20 cos25 sin20 sin25 cos20 sin20 cos25 s b cos a b cosa a sin 2 b 5 2 c 0 in os sin sinb 4 2 bulunur. 2 Cevap : C 2) sin 40 x cos 10 x sin x 10 cos x 40 ifadesinin değeri aşağıdakilerden hangisidir? 1 2 3 1 3 A) B) C) D) E) 2 2 2 2 2 Çözüm: sin 40 x cos 10 x sin x 10 cos x 40 ifadeye dikkat edersek direkt sinüs toplam açılımına benzemiyor. Burada şuna dikkat edeceğiz. kosinüs çift bir fonksiyondur.Yani; cos 10 x cos x 10 cos x 40 cos 40 x dir . sin 40 x cos x 10 sin x 10 cos 40 x sin 40 x x 1 10 sin30 bulunur. 2 Cevap : D 3) o sin75 cos15 sin15 cos75 ifadesinin eşiti aşağıdakilerden hangisidir? 1 2 3 1 3 A) B) C) D) E) 2 2 2 2 2 Çözüm: o sin75 cos15 sin15 cos75 ifadesinde sinüs fark açılımı kullanılmış. 1 sin 75 15 sin60 bulunur. 2 Cevap : D 4) Bir ABC üçgeninde, 2 m(A) ve cos(C) veriliyor. 3 3 Buna göre, sin(B) değeri aşaığıdakilerden hangisidir? 2 3 5 5 2 3 5 3 A) B) C) 6 6 6 5 2 3 3 5 D) E) 6 6 Çözüm: 2 Not : cosC ise C açısı geniş açıdır. 3 sinC pozitif olmalı. Dik üçgende C açısının bütünleri olan açıya x 2 dersek, x dar açı olur. cos x olur. 3 sinC sinx olur. Toplam Fark Formülleri 2 2 2 2 a 2 3 a 9 4 5 a 5 olur. 5 5 sinx olur. sinC olur. 3 3 ABC üçgen olduğundan; m(A) m(B) m(C) dir. 2 m(B) m(C) m(B) m(C) tür. 3 3 2 m(B) m(C) dir. 3 2 sin(B) sin m( 3 2 5 3 3 3 1 2 2 C) dir. 2 2 sin(B) sin cos(C) sin(C) cos 3 3 2 3 5 5 2 3 sin(B) bulunur. 6 6 6 Cevap : B 5) sin70 sin80 cos80 cos70 ifadesinin eşiti aşağıdakilerden hangisidir? 3 1 2 3 1 A) B) C) D) E) 2 2 2 2 2 Çözüm: u H c at sin70 sin80 cos80 cos70 cos80 cos70 sin70 sin80 cos 80 70 os 150 cos 180 30 3 cos30 n c ırlatma: cosa cosb sina sinb cos a b i os30 b 2 cosa cosb s na si b cos a b lunur. Cevap : A 6) cos105 ifadesinin eşiti aşağıdakilerden hangisidir? 6 2 6 2 2 6 A) B) C) 4 4 4 3 2 3 2 D) E) 2 2 Çözüm: cos 105 cos 60 45 cos60 cos45 sin60 .sin45 1 2 3 2 2 2 2 2 2 6 bulunur. 4 Cevap : C 7) 4 5 4 5 cos cos sin sin ifadesinin 9 18 9 18 eşiti aşağıdakilerden hangisidir? 1 3 2 3 1 A) B) C) D) E) 2 2 2 2 2 ÇÖZÜM: 2 4 5 4 5 cos cos sin sin 9 18 9 18 4 5 8 5 3 cos cos cos 9 18 18 18 3 cos dir. 6 2 Cevap : B 8) 2 2 2 sin50 a olduğuna göre, cos10 3 cos80 ifadesinin eşiti aşağıdakilerden hangisidir? A) a B) 2a C) 2 1 a D) 1 a E) a 1 Çözüm: Toplam Fark Formülleri tan60 sin10 2 2 2 2 2 sin50 a , sin60 cos10 3 cos80 cos10 sin10 cos60 cos10 cos60 sin60 sin10 cos60 cos 60 10 2 cos50 1 2 Şimdi cos 50 yi bulalım. sin x cos x 1 cos x 1 sin x olduğundan; cos 50 1 a 2 2 2 cos50 1 a 2.cos50 2 1 a bulunur. Cevap : C 9) 2 2 x y 4 sinx cos y siny cosx ifadesinin değeri aşağıdakilerden hangisidir? A) 1 2 B) 1 2 C) 2 2 2 D) 2 E) 2 2 2 Çözüm: 2 2 2 2 2 2 2 2 2 2 1 1 x y 4 sinx cos y sin x 2.sinx.cos y cos y siny cosx sin y 2siny.cosx cos x Taraf tarafa toplarsak, sin x cos x sin y cos y 2(sinx.cos y siny.cosx) 2 2 sin x y 2 2 sin 2 2 4 2 2 2 2 bulunur. Cevap : E 10) 1 sin arctan 3 arccos 2 ifadesinin değeri aşağıdakilerden hangisidir? 1 1 A) B) 1 C) 0 D) E) 1 2 2 Çözüm: 1 sin arctan 3 arccos 2 arctan 3 tan 3 arctan ın değer kümesi , dir. 2 2 Pozitif değer olduğundan 1. bölgededir. 1 1 arccos cos 2 2 arcos un değer kümesi 0, aralığındadır. 1 cos 2. bölgede negatiftir. Kosinüsün olduğu 2 dar açıyı bulup, bu açıyı 180 ‘den çıkarmalıyız. Şimdi dar açılı dik üçgenlerde bu değerleri yerleştirelim. Dikkat edersek 60 dir. Çünkü tan60 3 tür. 1 1 cos60 cos 180 60 2 2 1 cos120 dir. 120 dir. 2 sin sin 60 120 sin180 0 dır. Cevap : C
 Bu bölümde Toplam Fark Formülleri ile ilgili 21 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…
Bu bölümde Toplam Fark Formülleri ile ilgili 21 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…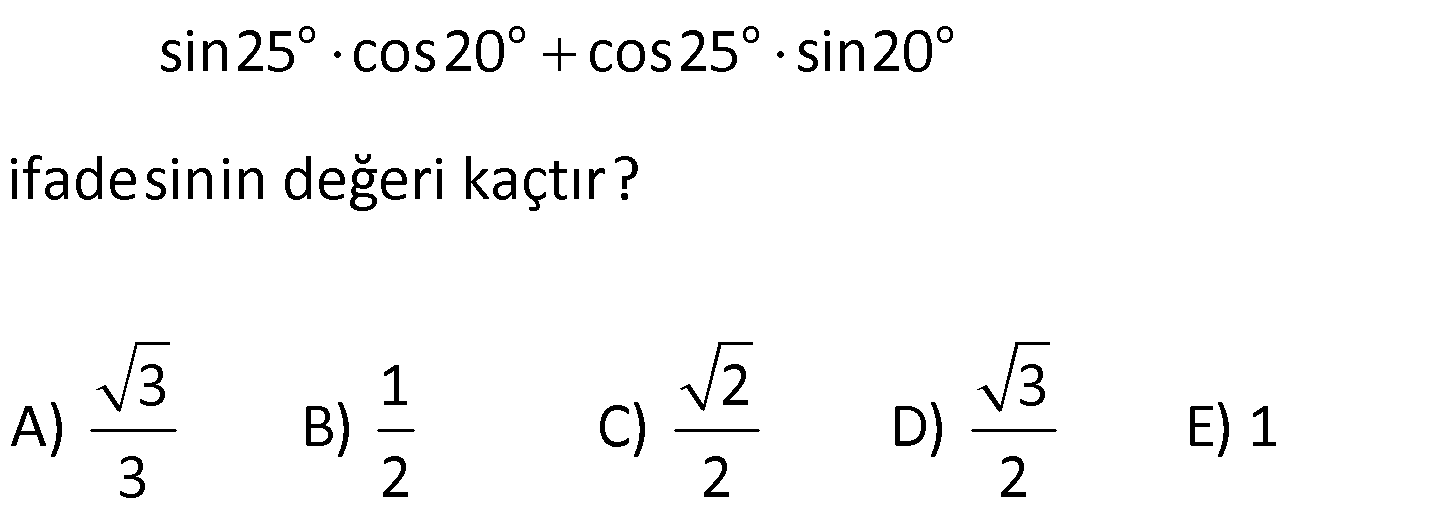

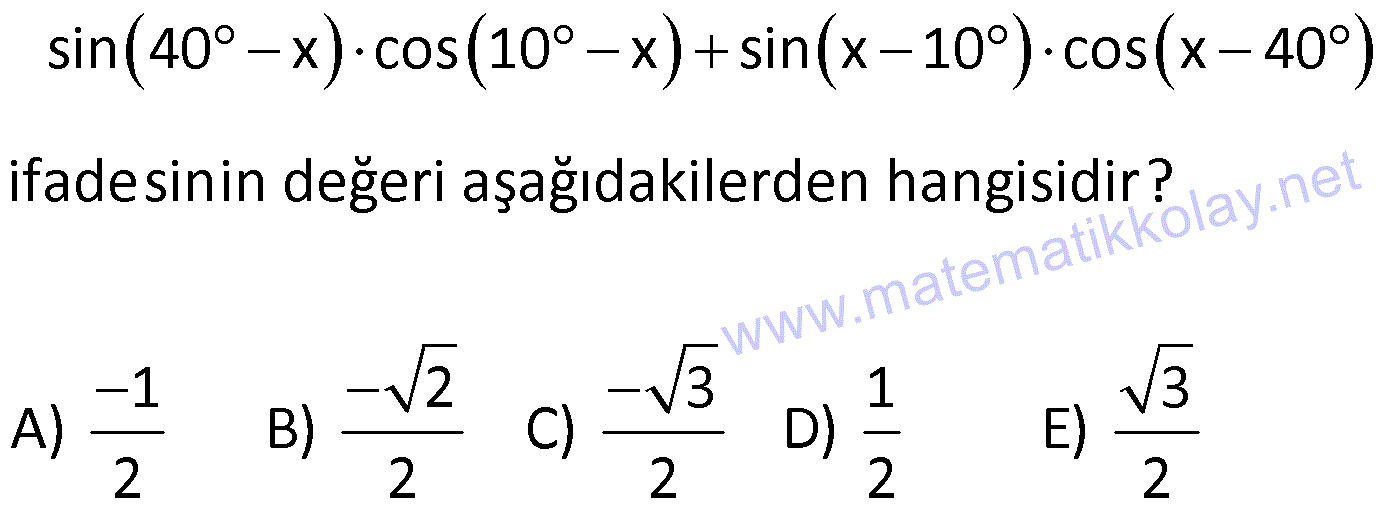

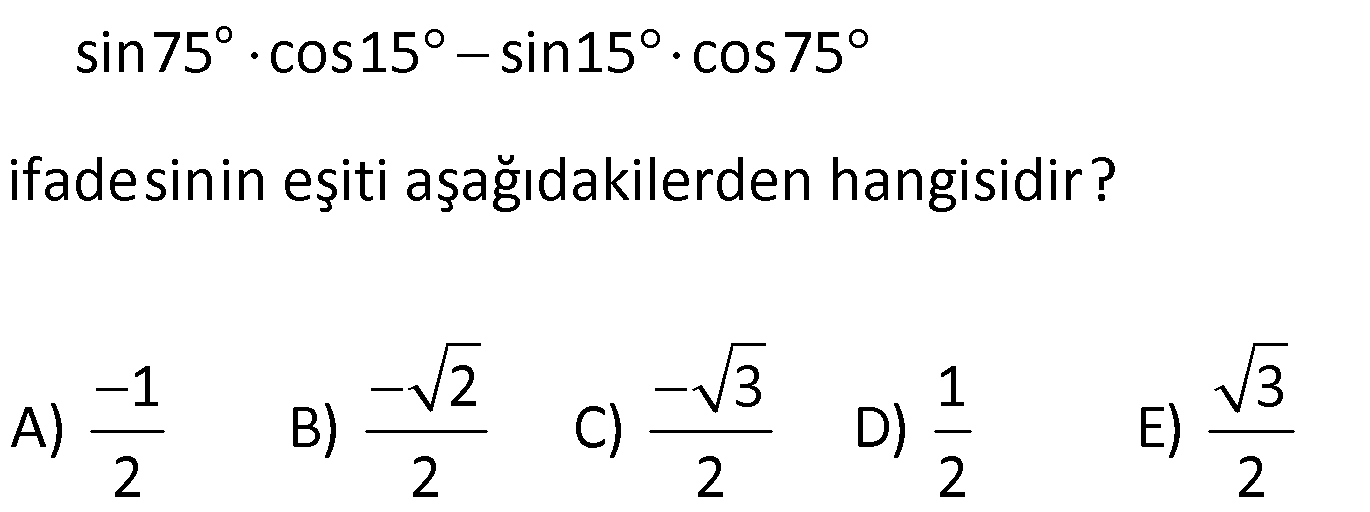
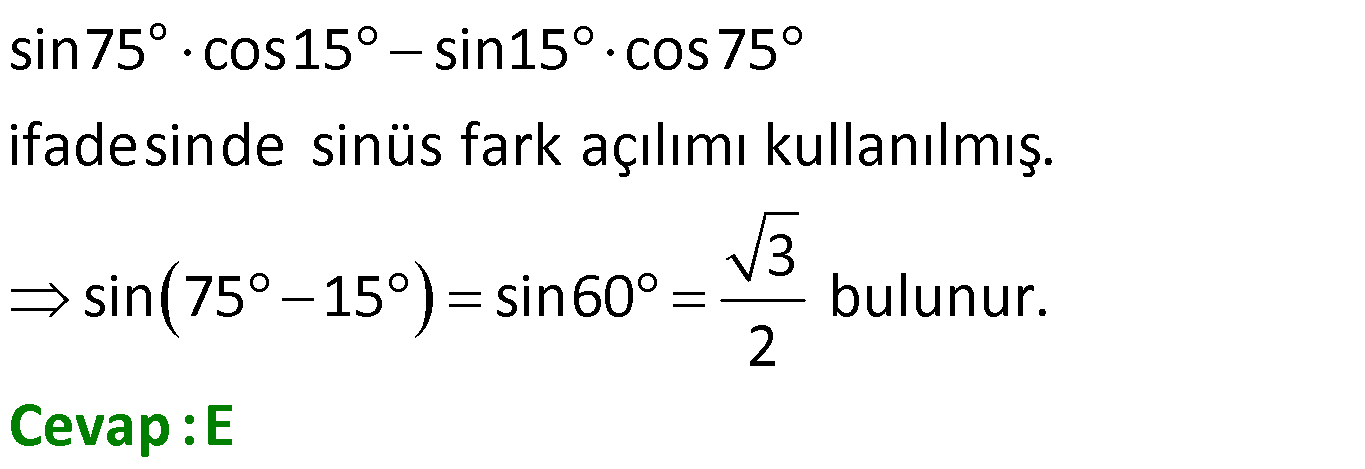


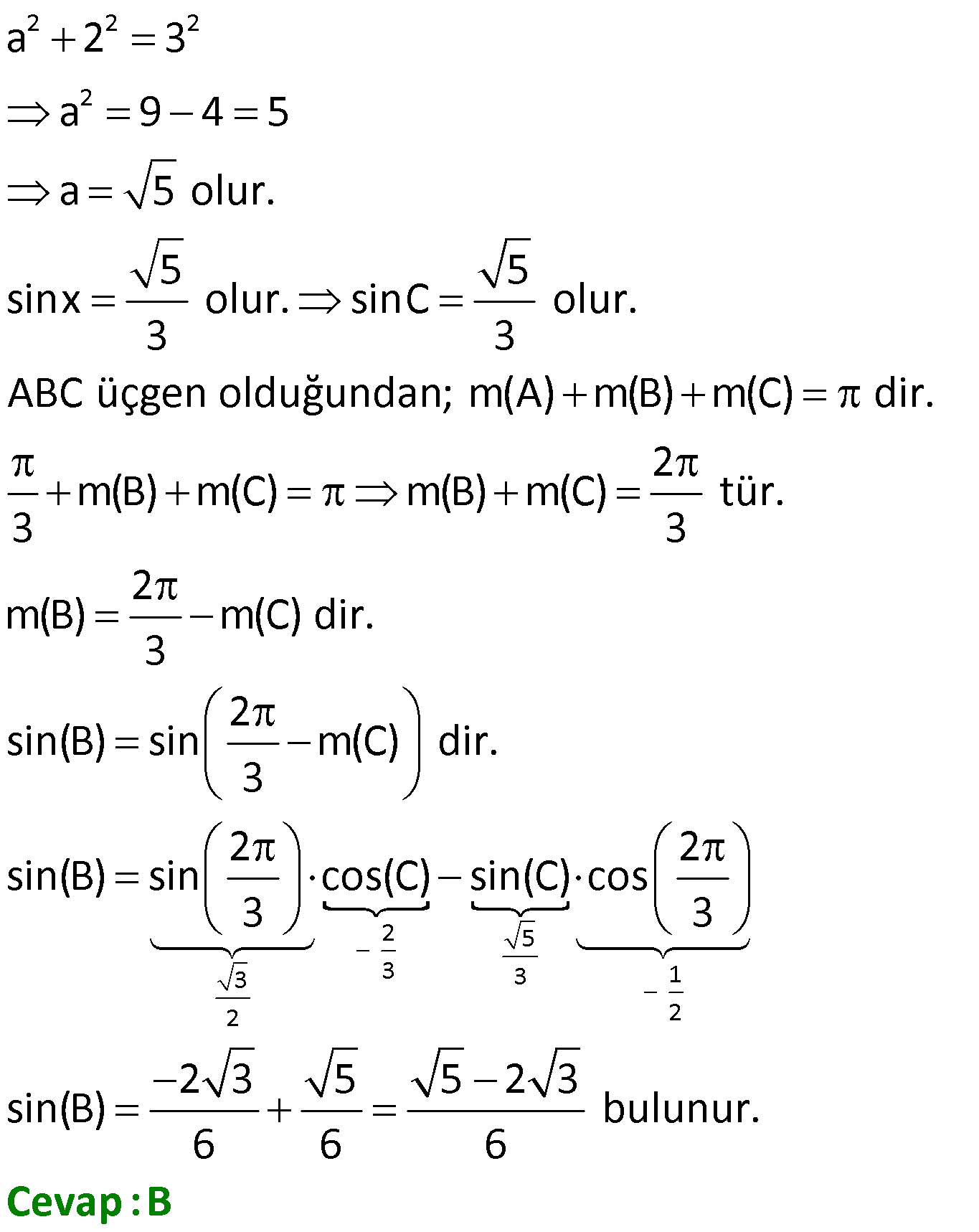



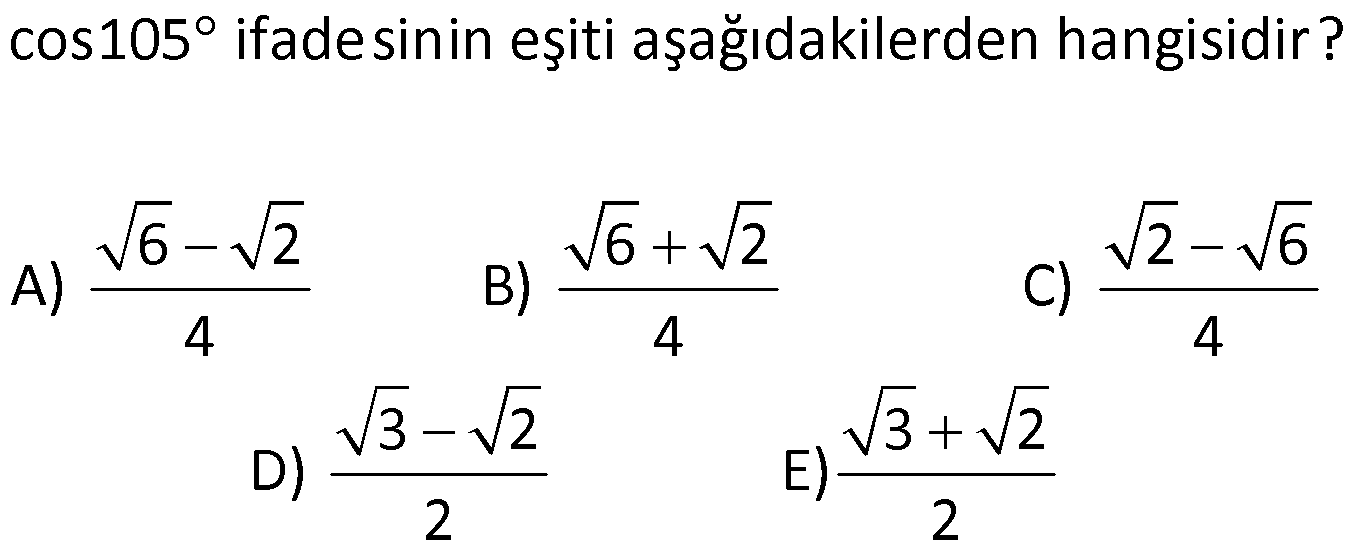
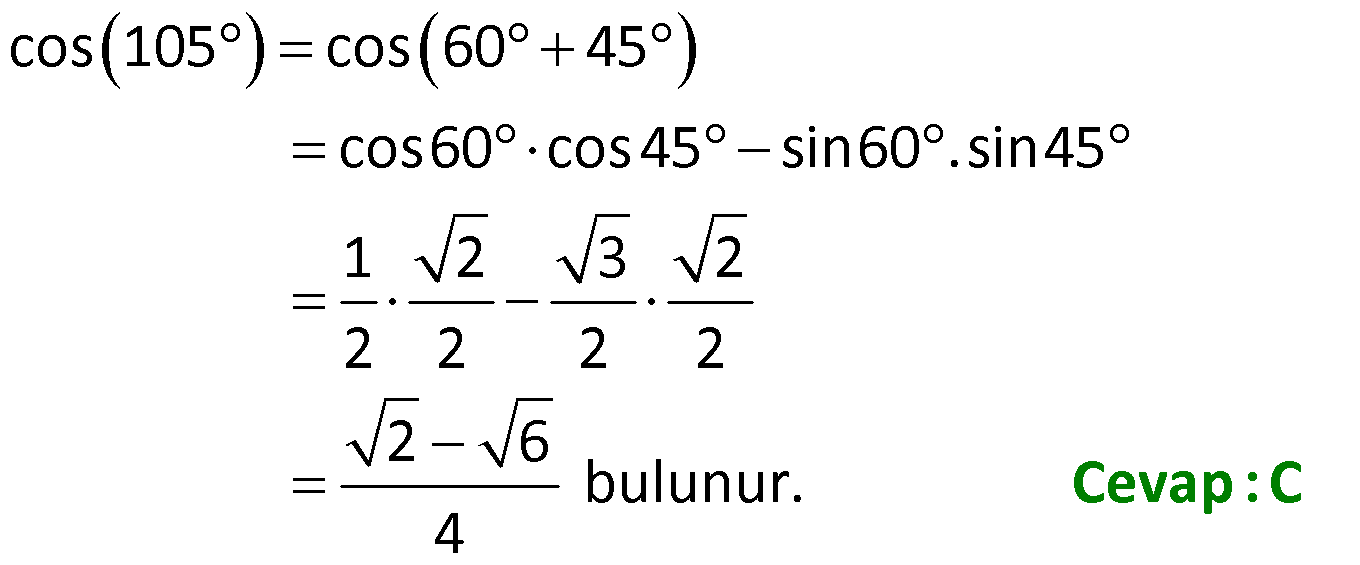
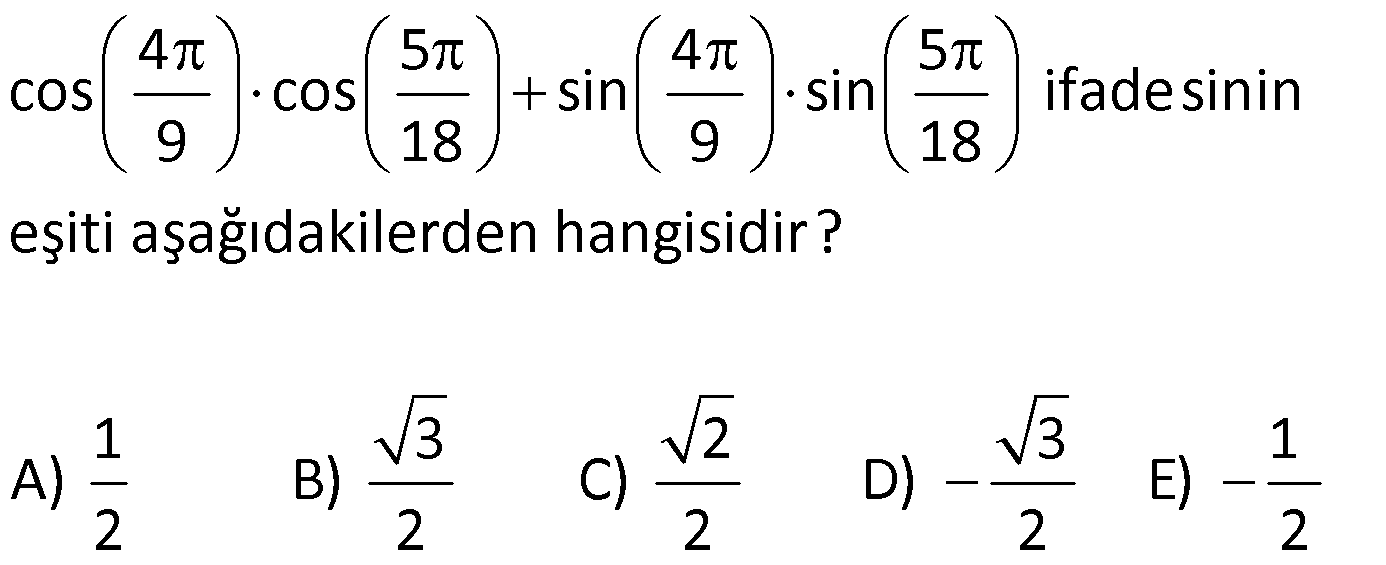
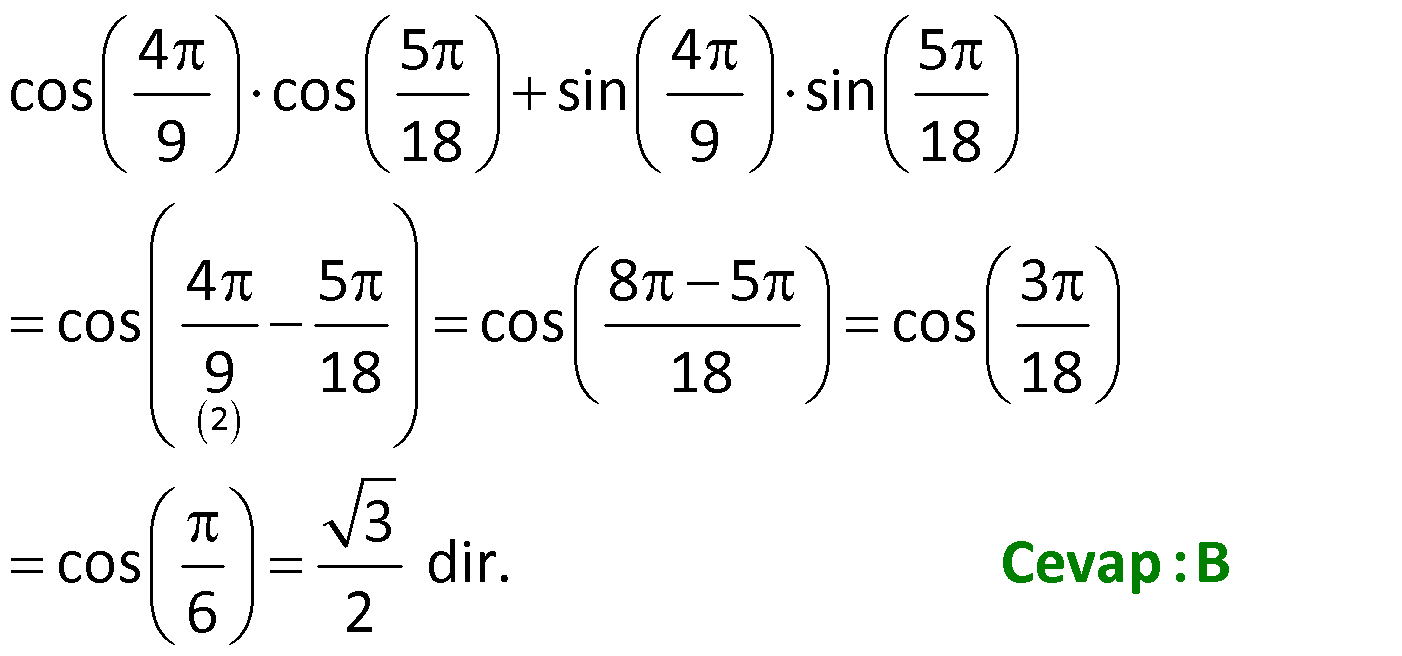


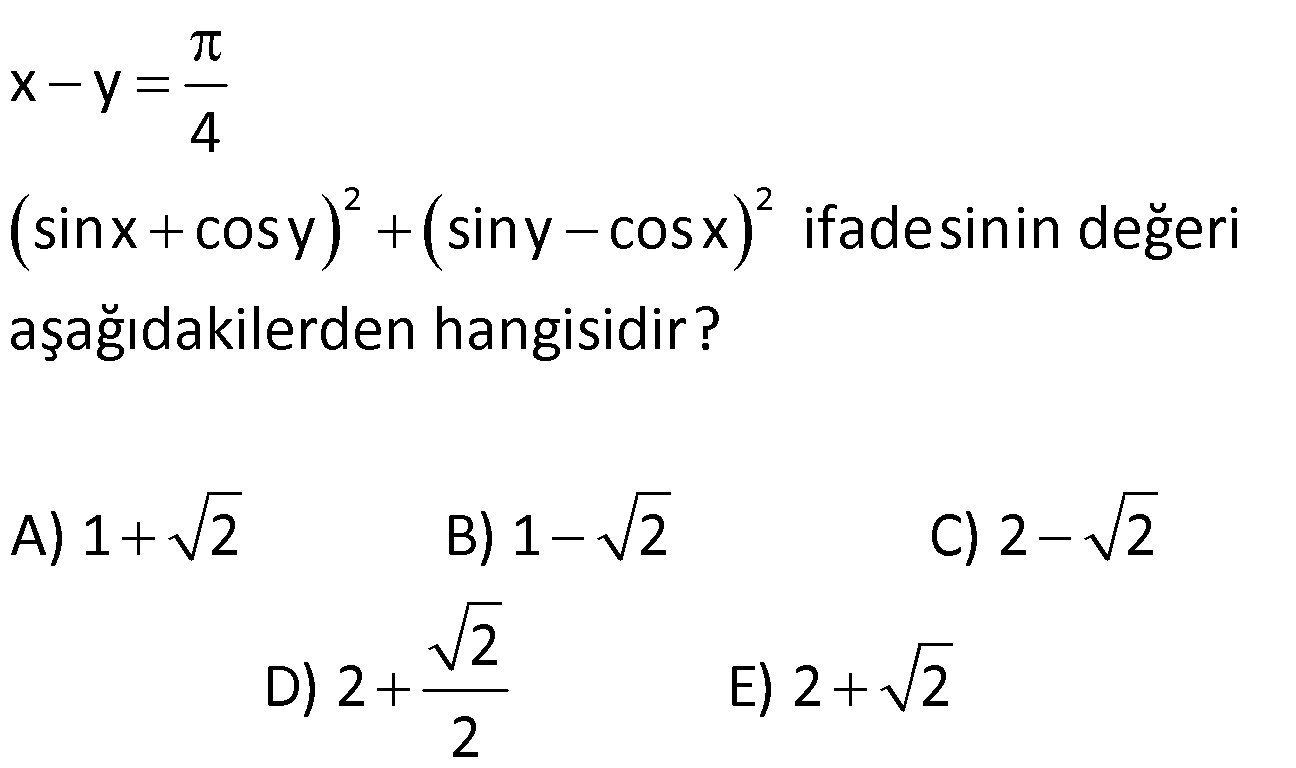

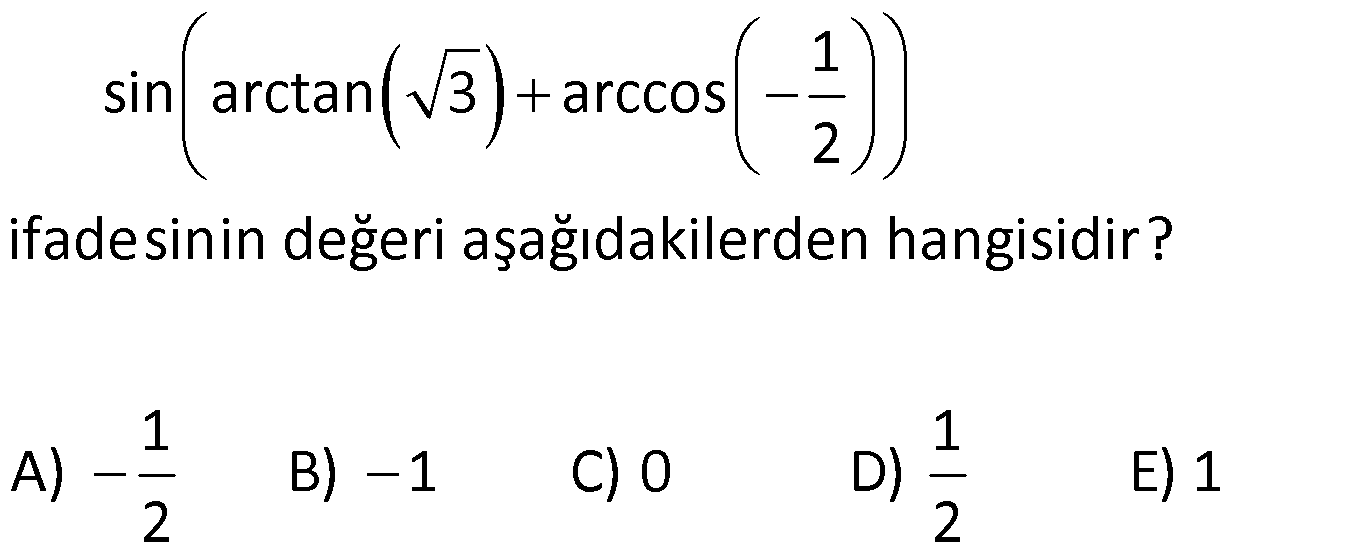

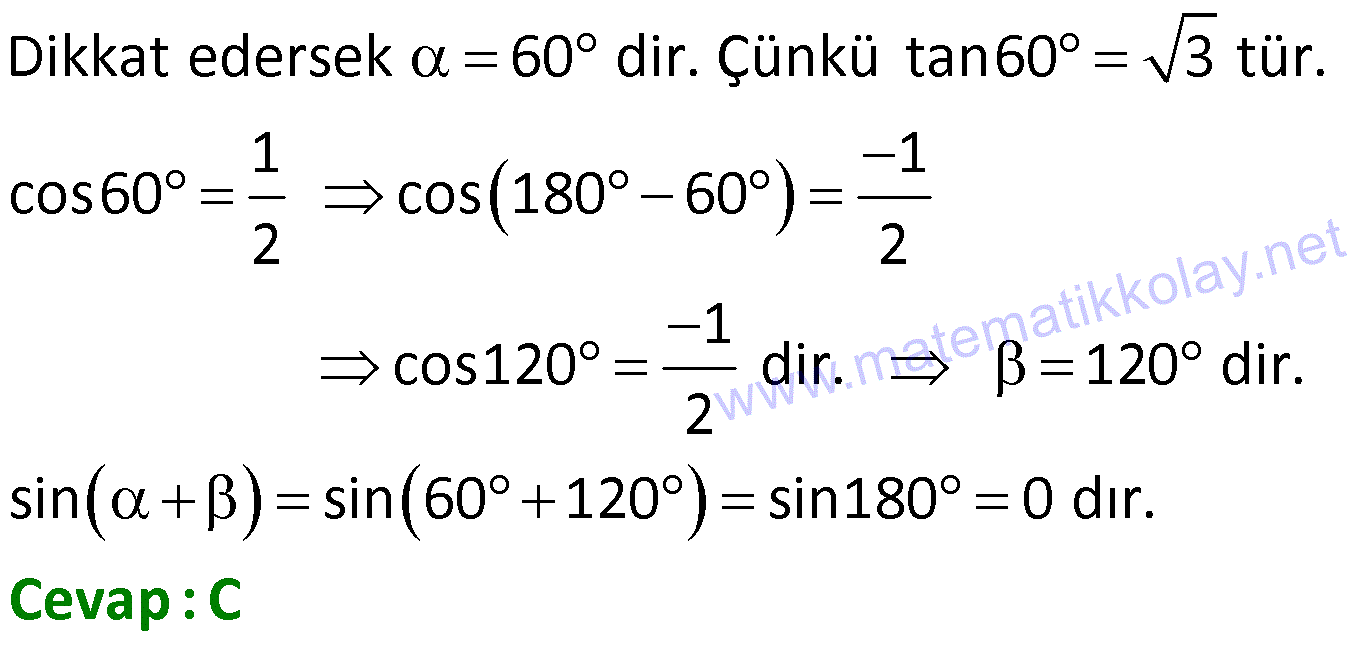


hocam bazı sorularınız yanlış sin 60 a kök3 bölü 2 yerine 1bölü 2 demişsiniz
Uyarınız için teşekkürler. Bariz bir hata varmış, gözümüzden kaçmış. Şimdi düzeltildi.