Bu bölümde Açık Önerme ve Niceleyiciler ile ilgili 11 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…
1.SORU
 |  |  |  |  |
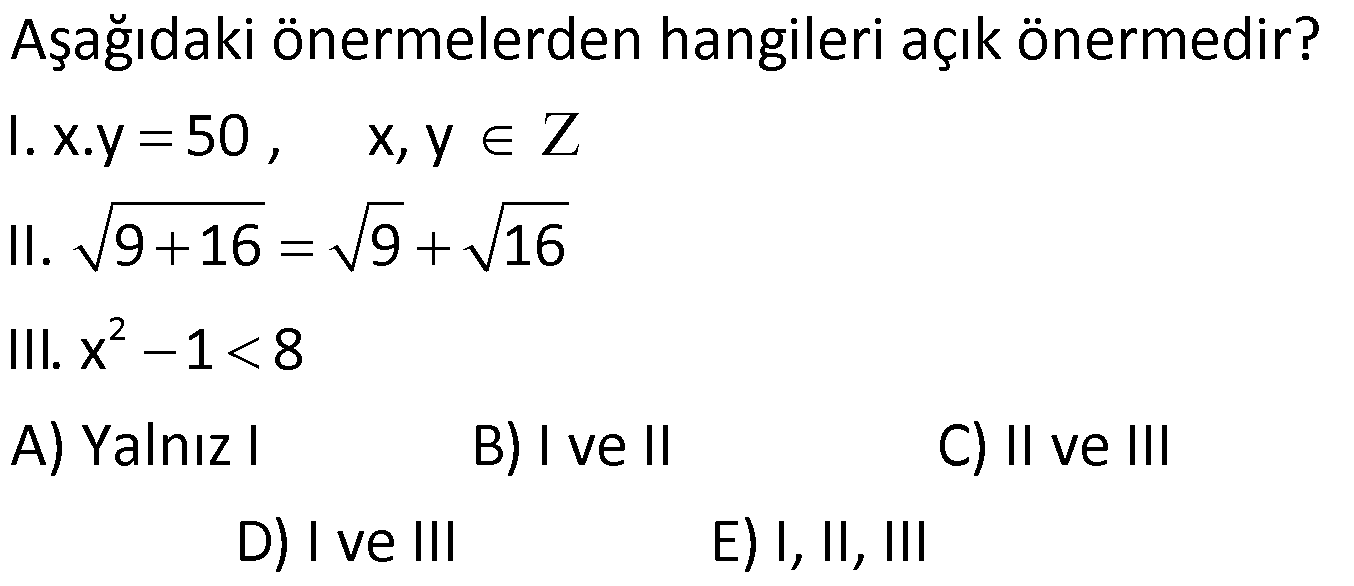
Çözüm için Tıklayınız.
2.SORU
| | | | | |
Çözüm için Tıklayınız.
3.SORU
| | | | | |
Çözüm için Tıklayınız.
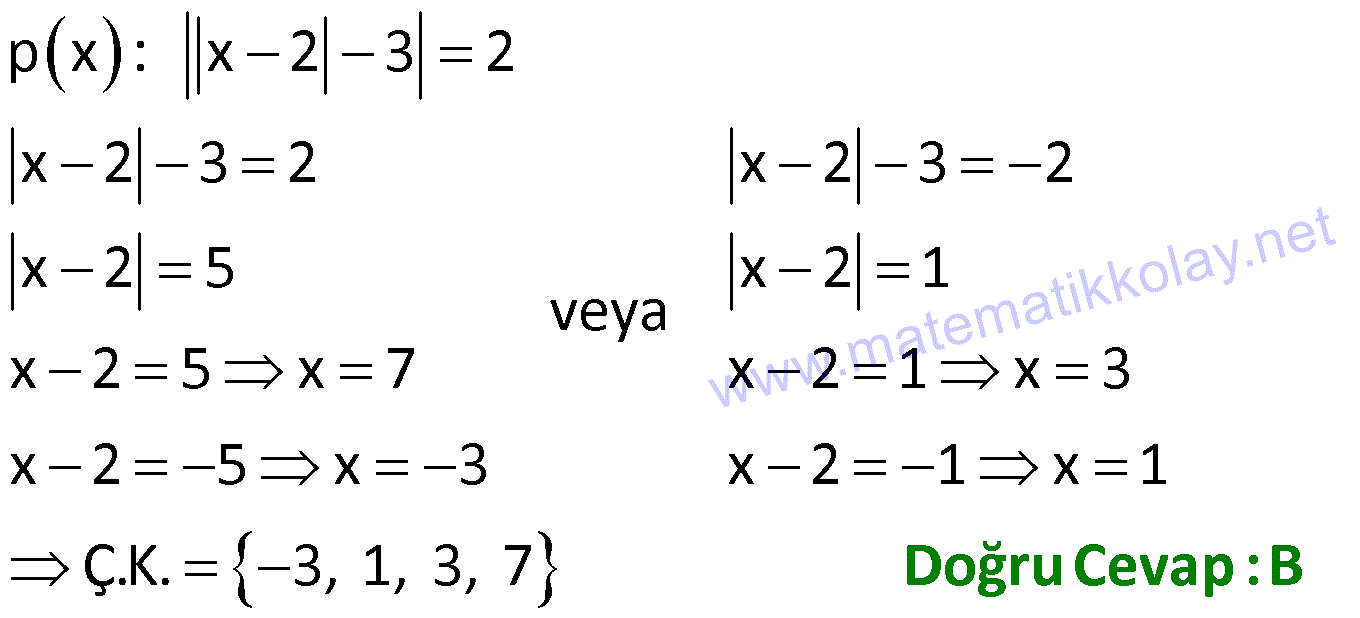
4.SORU
| | | | | |
Çözüm için Tıklayınız.
5.SORU
| | | | | |
Çözüm için Tıklayınız.
6.SORU
| | | | | |
Çözüm için Tıklayınız.
7.SORU
| | | | | |
Çözüm için Tıklayınız.
8.SORU
| | | | | |
Çözüm için Tıklayınız.
9.SORU
| | | | | |
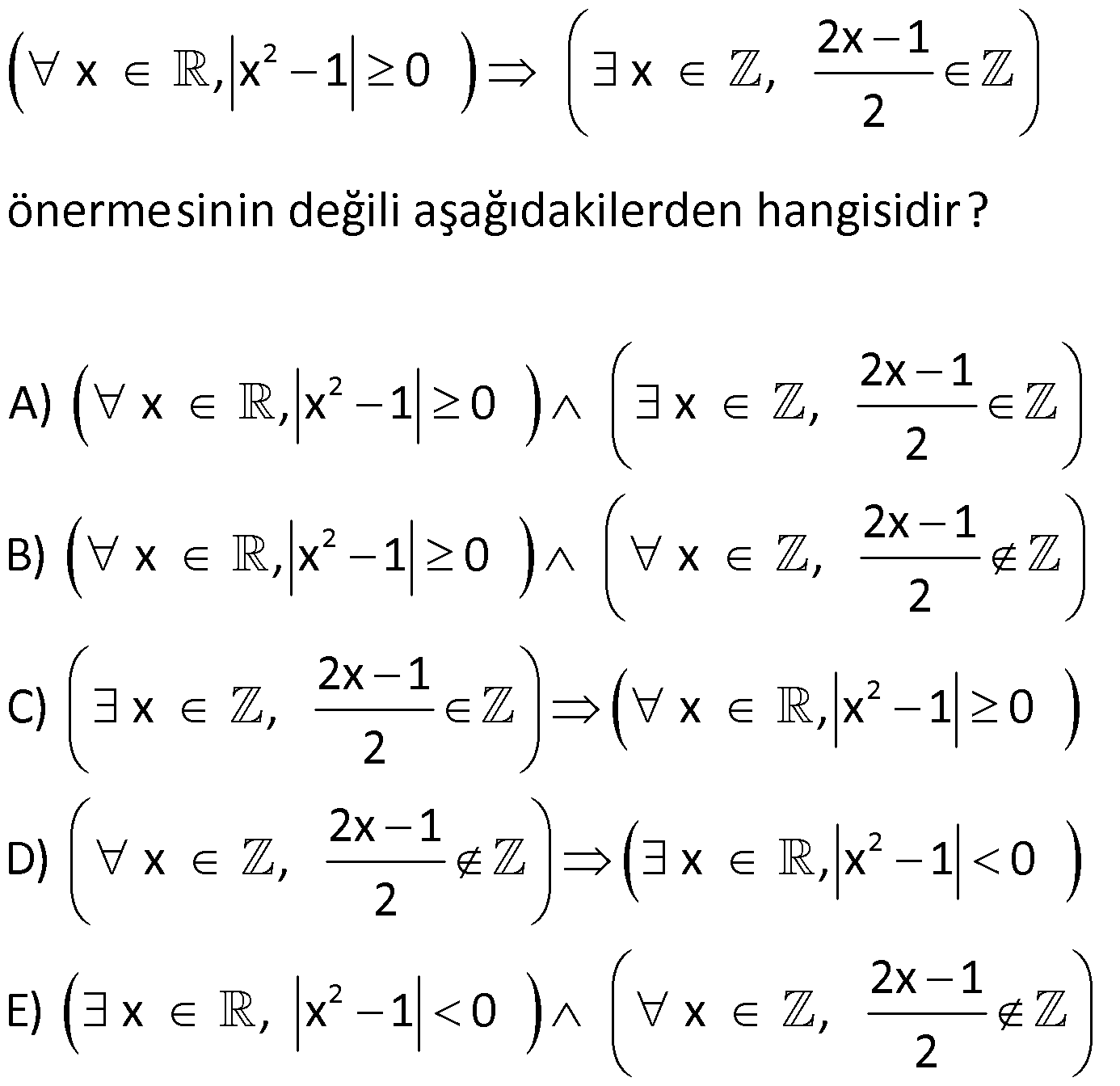
Çözüm için Tıklayınız.
10.SORU
| | | | | |
Çözüm için Tıklayınız.
11.SORU
| | | | | |
Çözüm için Tıklayınız.
Eğer sorular ya da çözümler konusunda bir problem görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.
Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)
AÇIK ÖNERME VE NİCELEYİCİLER 1) 2 Aşağıdaki önermelerden hangileri açık önermedir? I. x.y 50 , x, y II. 9 16 9 16 III. x 1 8 A) Yalnız I B) I ve II C) II ve III D) I ve III E) I, II, II I Çözüm: İçinde en az bir değişken bulunan ve bu değişken lere verilen değerlere göre doğruluğu ya da yanlış- lığı belirlenebilen önermelere açık önerme denir. Bir açık önermeyi doğrulayan elemanların kümesine d I. x.y 50 , x, y Bu önerme değişkenlere göre doğruluğu veya yanlışı belirlenebilir bir önerme olduğundan II. 9 16 9 16 önermesi değişkene bağlı olmadığın oğruluk kümesi denir i . açık önermed r. 2 dan III. x 1 8 önermesi değişkenlere göre doğruluğu veya yanlışlığı belirlene açık önermedir. bilir bir öne e rme olduğu i n açık önerm değ ldir. dan Cevap: D 2) 2 2 p x ,y : “x y 19” , x, y açık önermesinin doğruluk kümesinin eleman sayısı kaçtır? A) 1 B) 2 C) 3 D) 4 E) 5 Çözüm: 2 2 1 19 19 1 1 19 19 1 x y 19 x y x y 19 x y 1 x y 19 2x 20 x 10 , y 9 dur. 10,9 Diğer denklemleri de benzer şekilde çözersek 10, 9 , 10, 9 , 10,9 bulunur. Çözüm kümesi 4 elemanlıdır. Cevap : D 3) p x : x 2 3 2 açık önermesi veriliyor. Hangi x değeri için bu önermenin doğruluk değeri 0’dır? A) 3 B) 1 C) 1 D) 3 E) 7 Çözüm: p x : x 2 3 2 x 2 3 2 x 2 3 2 x 2 5 x 2 1 veya x 2 5 x 7 x 2 1 x 3 x 2 5 x 3 x 2 1 x 1 Ç.K. 3, 1, 3, 7 Doğru Cevap : B 4) 2 2 2 2 Her reel sayının karesi pozitif bir reel sayıya eşittir. önermesinin sembolik ifadesi aşağıdakilerden hangisinde doğru verilmiştir? A) x , x B) x , x C) x , x D) x , x E 2 ) x , x Çözüm: Her ve Bazı sözcüklerine niceleyici denir. Her niceleyicisi bütün anlamına gelir.Bu sebeple evrensel niceleyici olarak adlandırılır ve sembolü ile gösterilir. Bazı niceleyicisi en az bir tane anlamına g “Her reel sayının karesi poziti elir.Bu sebeple varlıksal nicele f bir reel sayıya eşittir.” Burd yici olarak adlandırılır a her ifadesinin matemat ve iks sembolü ile göster el sembolü dir. s ilir. ayıy x ı 2 2 diye ifade edersek karesi x olur. Reel sayıların sembolü , pozitif reel sayıların sembolü dır. Buna göre verilen önermenin sembolik ifadesi x , x olur. Cevap : A AÇIK ÖNERME VE NİCELEYİCİLER 5) 2 x , x önermesinin sözel ifadesi aşağıdakilerden hangisidir? A) Bazı reel sayıların karesi 0 dır. B) Bazı reel sayıların karesi negatiftir. C) Her reel sayının karesi pozitif reel sayı değildir. D ) Bazı reel sayıların karesi pozitiftir. E) Bazı reel sayıların karesi pozitif reel sayı değildir. Çözüm: 2 2 x , x önermesinde ” ” sembolü bazı anlamındandır. x sembolüyle bu x değerlerinin karesinin pozitif reel sayı olmadığı ifade ediliyor. Önermenin sözel ifadesi; “Bazı reel sayıların karesi pozi tif reel sayı değildir.” Doğru Cevap : E 6) x 2 Aşağıda verilen önermelerden hangileri doğrudur? I. x, y ‘ , x y ‘ II. x , x III. x , x 1 A) Yalnız I B) I ve II C) Yalnız II D) II ve III E) I, II ve III Çözüm: irrasyonel sayı 4 x 0 I. x, y ‘ , x y ‘ ? x 2, y 2 olursa, x y 2 2 2.2 2 Her irrasyonel sayı için sağlanmaz II. x , x ? x 0 oldu I. öncül ğunda 0 yanlı tanımsızdır. x 2 olduğunda 2 ş. 2 2 2 2 1 tür. 4 Bazı x değerleri için tam sayı olmaz. III. x , x 1 Reel sayılarda x 0 dır. x 1 1 olur. Her reel sayı için pozitiftir II. öncül doğru. . III. öncül yanlış. Cevap : C 7) 2 2 2 2 2 2 x , x 1 0 önermesinin değili aşağıdakilerden hangisidir? A) x , x 1 0 B) x , x 1 0 C) x , x 1 0 D) x , x 1 0 E) x , x 1 0 Çözüm: 2 Not : niceleyicisinin değili ” ” dır. niceleyicisinin değili ” ” dir. sembolünün değili ” ” tir. sembolünün değili ” ” tir. sembolünün değili ” ” di x , x 1 0 önermesinin deği r. ı 2 2 linin alalım. x , x 1 0 x , x 1 0 dir. Cevap : D 8) 2 2 2 2 x , x 1 0 x , x önermesinin değili aşağıdakilerden hangisidir? A) x , x 1 0 x , x B) x , x 1 0 x , x C) x , x 1 0 x , x 2 2 D) x , x 1 0 x , x E) x , x 1 0 x , x AÇIK ÖNERME VE NİCELEYİCİLER Çözüm: 2 ı 2 ı ı 2 2 x , x 1 0 x , x önermesinin değilini alalım. x , x 1 0 x , x x , x 1 0 x , x x , x 1 0 Not : p q ‘ p’ q’ , p q ‘ p’ q’ x , x dir. Cevap : D 9) 2 2 2 2x 1 x , x 1 0 x , 2 önermesinin değili aşağıdakilerden hangisidir? 2x 1 A) x , x 1 0 x , 2 2x 1 B) x , x 1 0 x , 2 2x C) x , 2 2 2 1 x , x 1 0 2 2x 1 D) x , x , x 1 0 2 2x 1 E) x , x 1 0 x , 2 Çözüm: 2 ı 2 ı ı 2 2x 1 x , x 1 0 x , 2 önermesinin değilini alalım. 2x 1 x Not : p q ‘ , x 1 0 x , 2 2x 1 x , p’ q ‘ p q’ dir. x 1 0 x , 2 x , ı ı ı 2 2 2x 1 x 1 0 x , 2 2x 1 x , x 1 0 x , 2 Cevap : B 10) 3 2 2 3 2 3 2 3 3 2 3 2 x 1 9 x 1 5 önermesinin karşıt tersi aşağıdakilerden hangisidir? A) x 1 5 x 1 9 B) x 1 5 x 1 9 C) x 1 5 x 1 9 D) x 1 9 x 1 5 E) x 1 9 x 1 5 Çözüm: 3 2 2 3 2 3 x 1 9 x 1 5 önermesinin değili x 1 5 ‘ x 1 Not :p q önermesinin karşıt te 9 ‘ x 1 5 x 1 9 dir. rsi q’ p’ dir. Cevap : A 11) b Aşağıdaki verilen ifadelerden hangileri doğrudur? I.” Düzlemde iki noktadan yalnızca bir doğru geçer.” ifadesi bir aksiyomdur. II. “a ve b tek doğal sayı ise a ifadesi tek doğal sayıdır.” teoreminin hipotezi: “a ve b tek doğal sayıdır.” a III. “a ve b tamsayı ve b 0 olmak üzere şeklinde b ifade edilebilen sayılara rasyonel sayılar denir.” ifadesi bir tanımdır. A) Yalnız I B) Yalnız II C) I ve II D) II ve III E) I, II, III Çözüm: AÇIK ÖNERME VE NİCELEYİCİLER Bir kavramın niteliklerini eksiksiz olarak belirtme ve açıklamaya tanım denir. Doğruluğu ispatsız kabul edilen önermelere aksiyom denir. Doğruluğu ispatlanması gereken önermelere teorem denir. p q önermes Düzlemde iki noktadan yalnızca bir doğru geçer. ifadesinin doğruluğu ispatsız kab inde p önermesi hip ul edildiğinden aksi otez varsayım q önermesi h yomdur. I. öncül doğru “a üküm yargı d ve b tek ür. doğal b sayı ise a ifadesi tek doğal sayıdır.” ifadesi bir hipotez ve hükümden oluştuğu için teoremdir. II. öncül doğru a “a ve b tamsayı ve b 0 olmak üzere şeklinde b ifade edilebilen sayılara rasyonel sayıla r denir.” verilen ifade rasyonel sayıları eksiksiz bir şekilde ifade ettiği için bi Doğr r ta u Ce nımd va ır. p : E
