Bu bölümde Üçgende Benzerlik ile ilgili 20 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…
1.SORU
 |  |  |  |  |
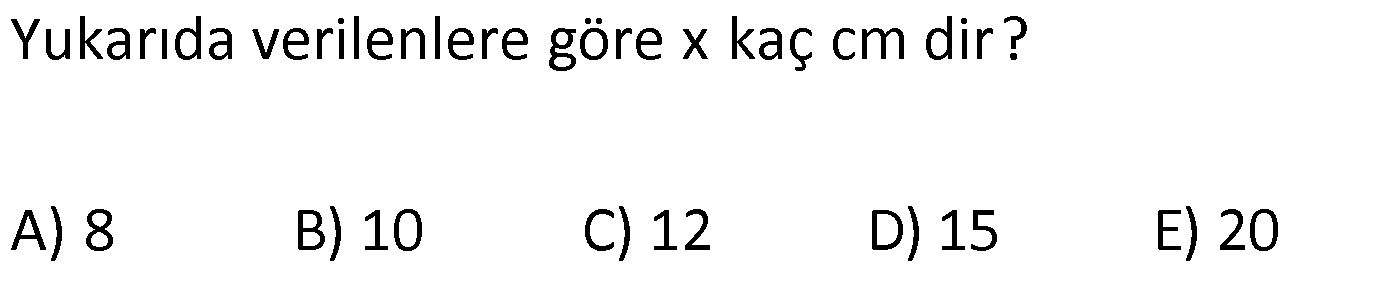
Çözüm için Tıklayınız.
2.SORU
| | | | | |
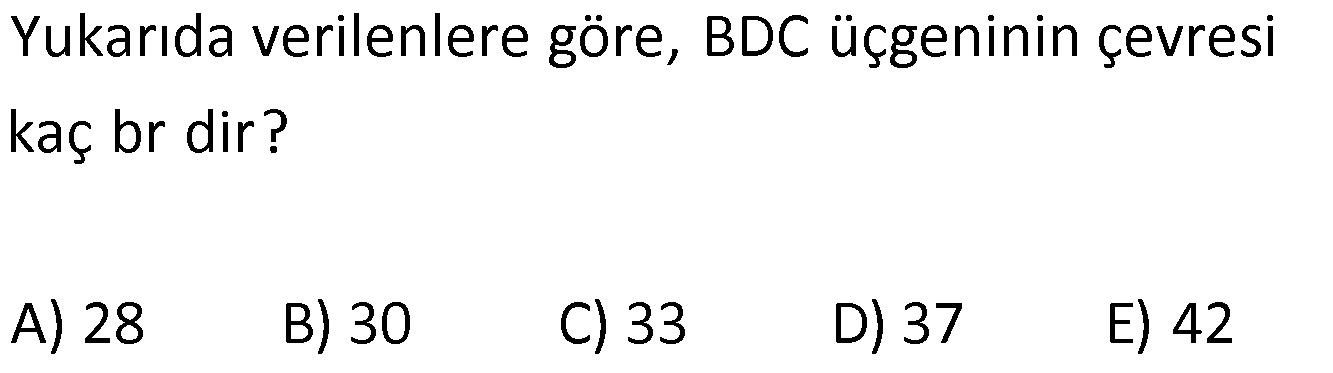
Çözüm için Tıklayınız.
3.SORU
| | | | | |
Çözüm için Tıklayınız.
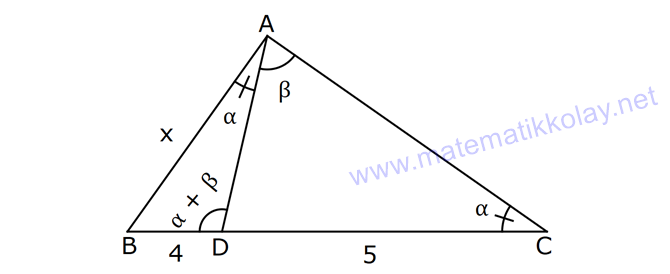
4.SORU
| | | | | |
Çözüm için Tıklayınız.
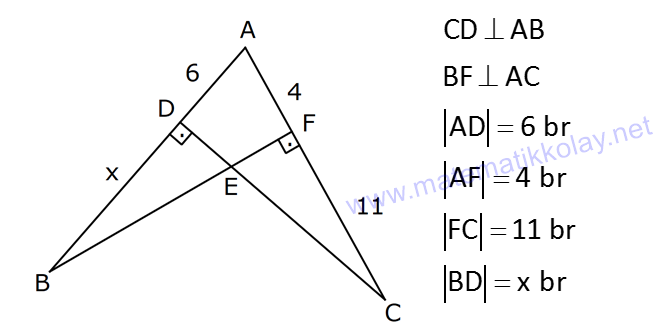
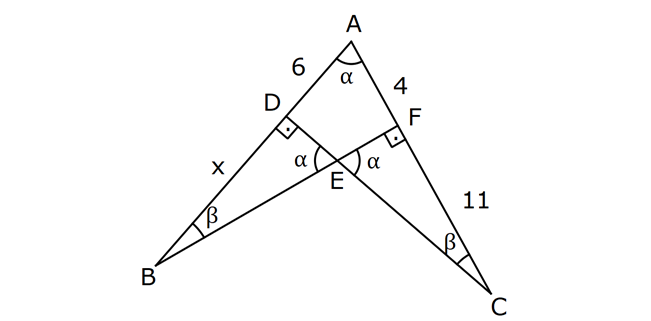
5.SORU
| | | | | |
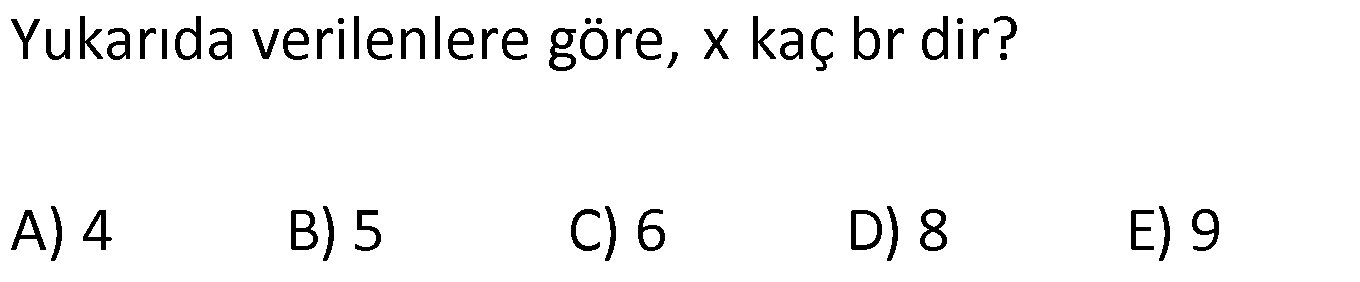
Çözüm için Tıklayınız.
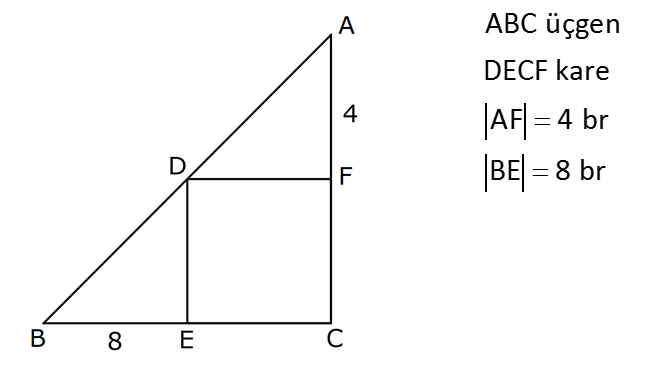
6.SORU
| | | | | |
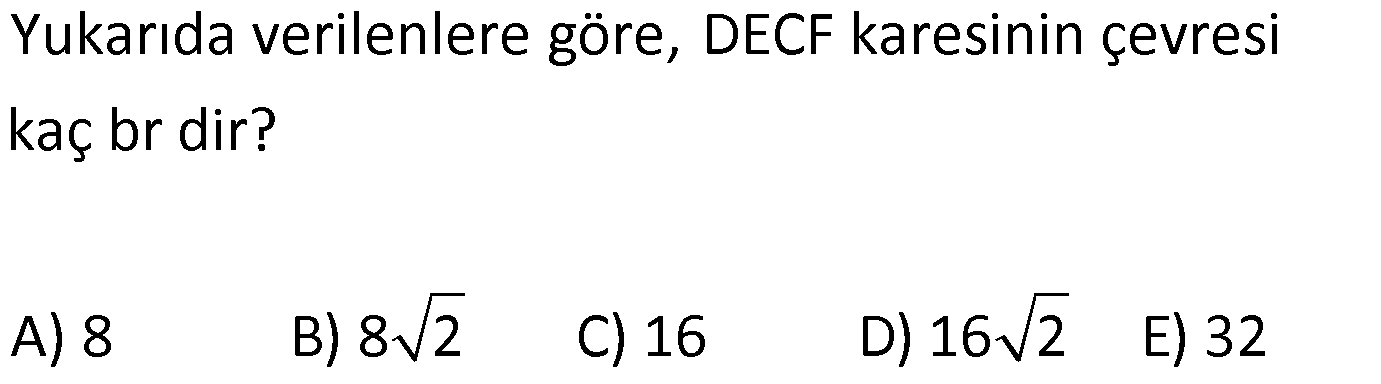
Çözüm için Tıklayınız.
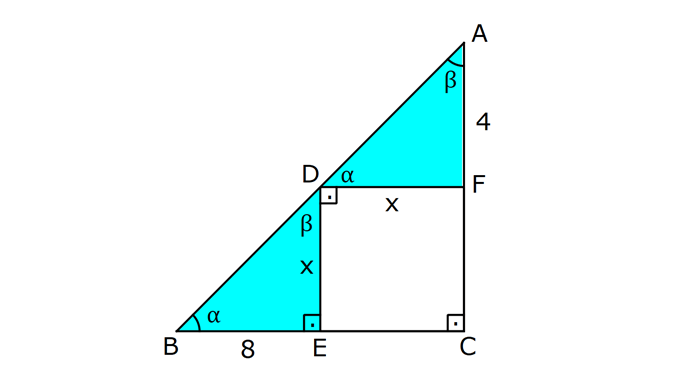
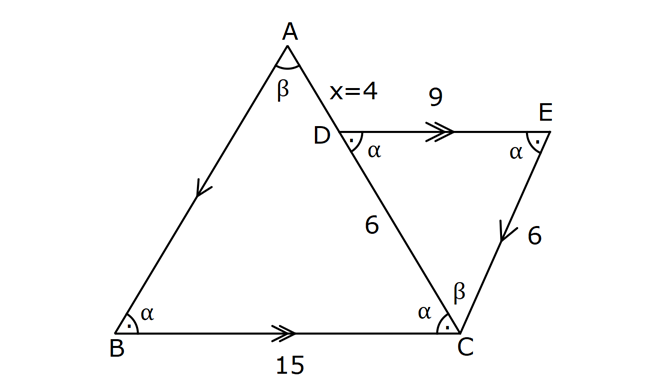
7.SORU
| | | | | |
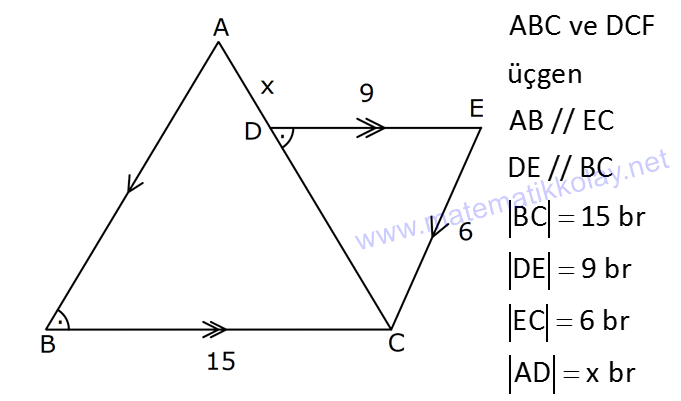
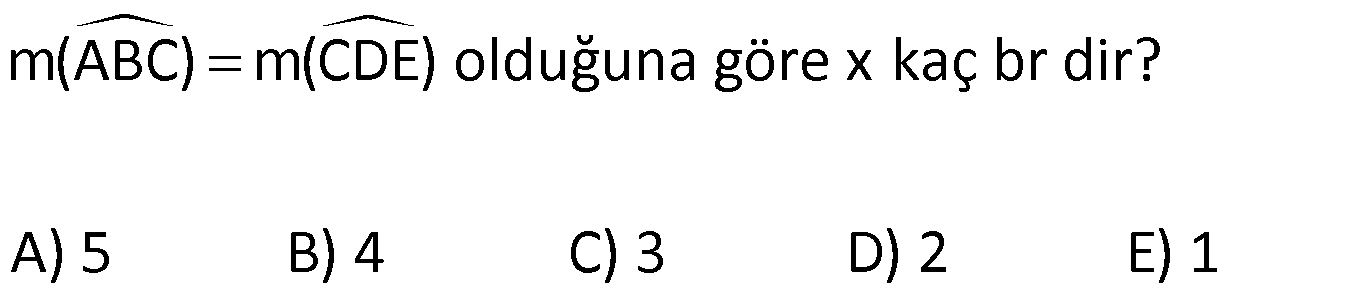
Çözüm için Tıklayınız.
8.SORU
| | | | | |
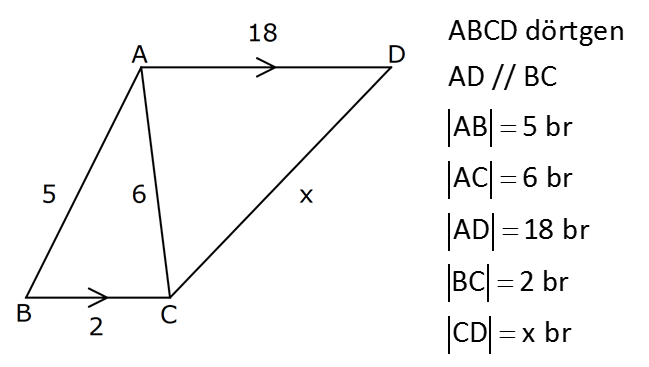
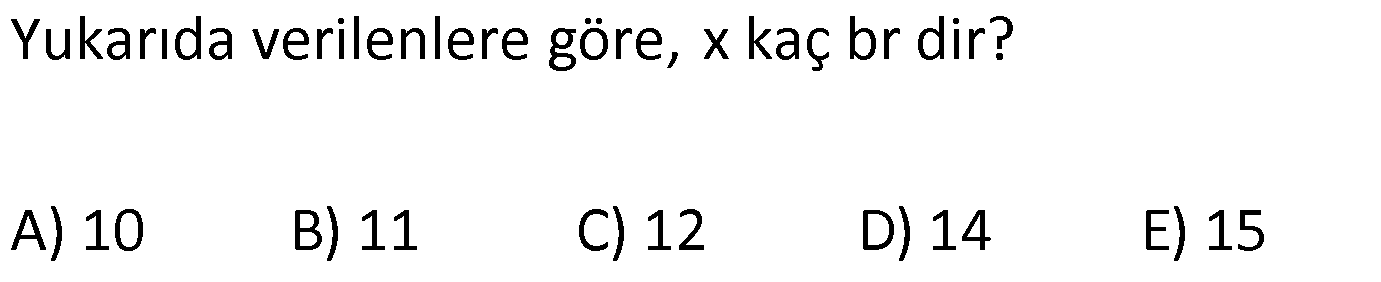
Çözüm için Tıklayınız.
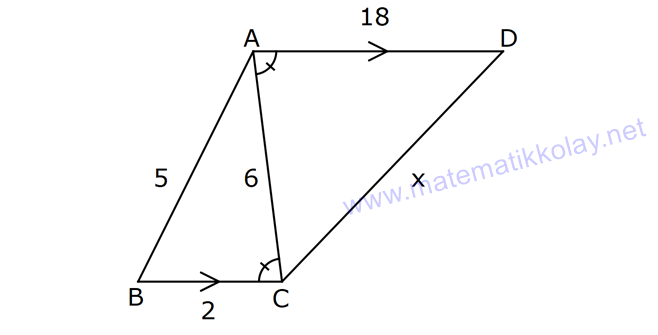
9.SORU
| | | | | |
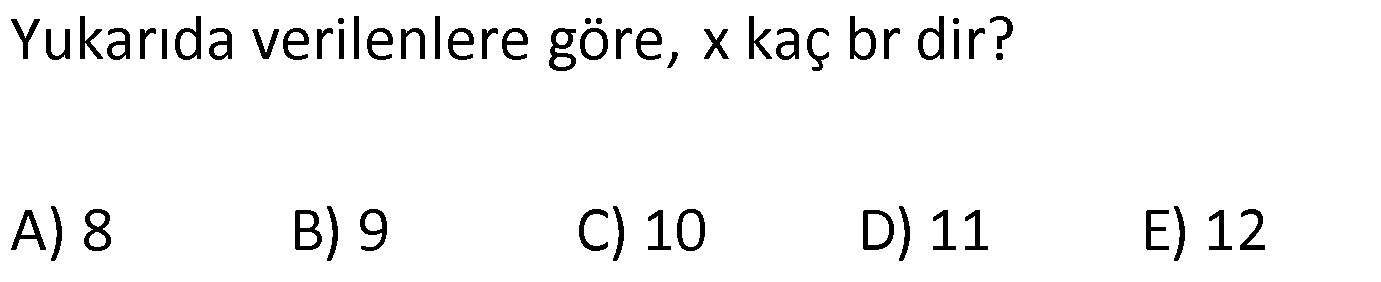
Çözüm için Tıklayınız.
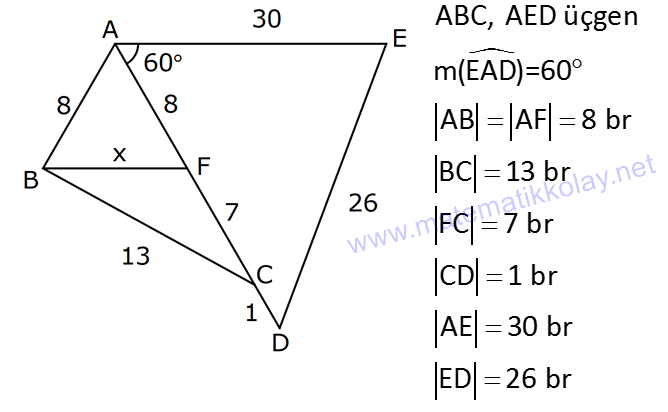
10.SORU
| | | | | |
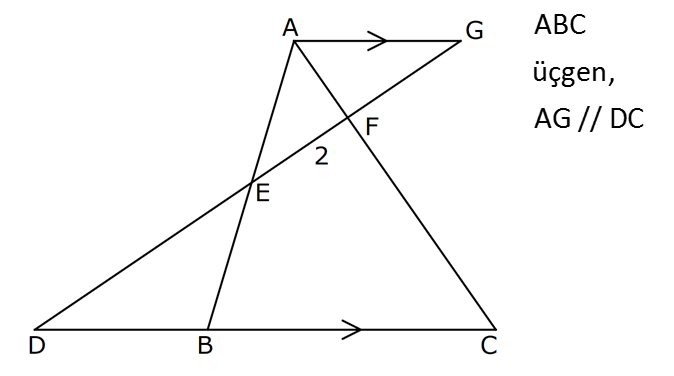
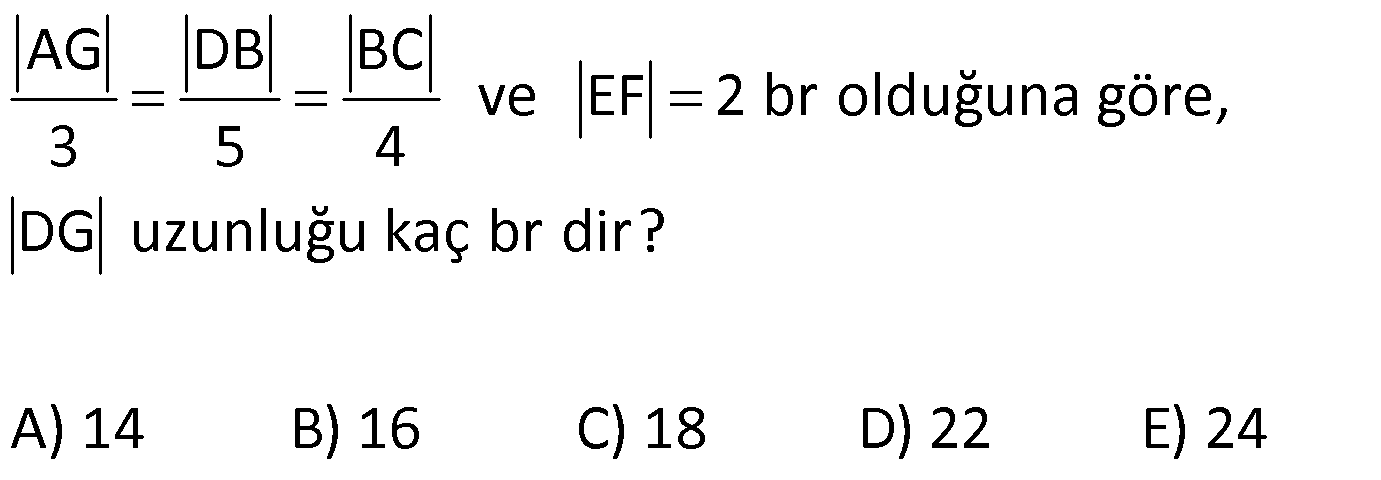
Çözüm için Tıklayınız.
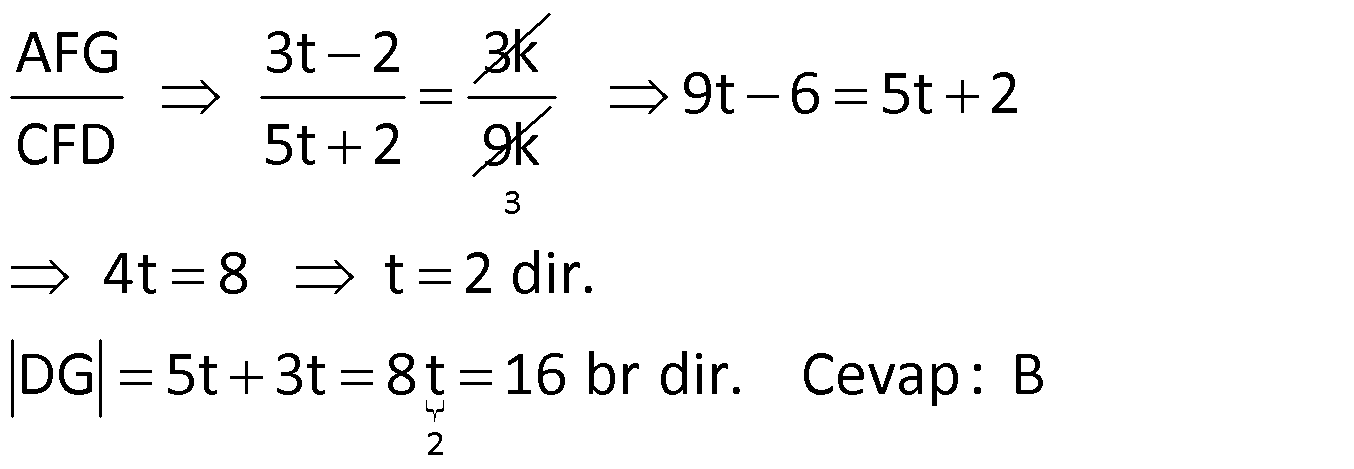
Eğer sorular ya da çözümler konusunda bir problem görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.
Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)
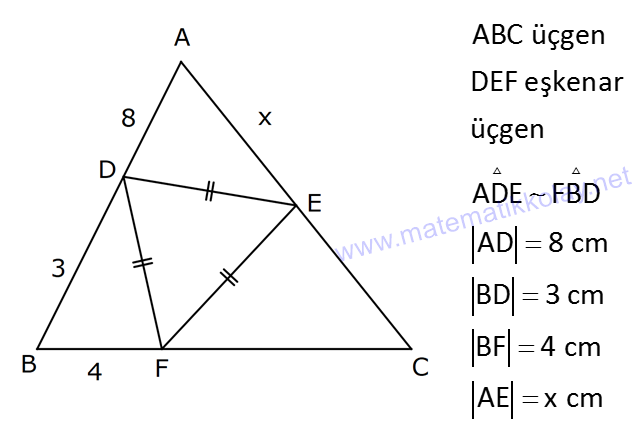
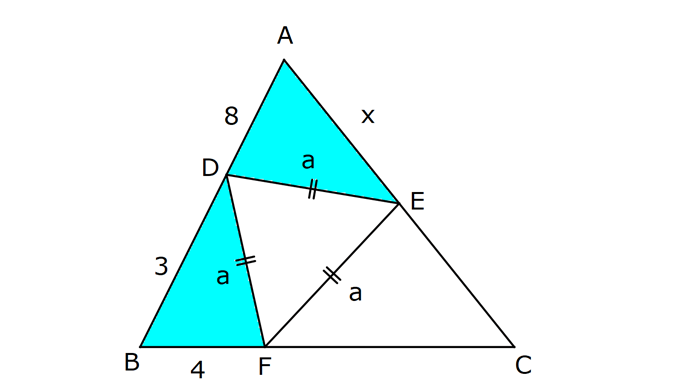
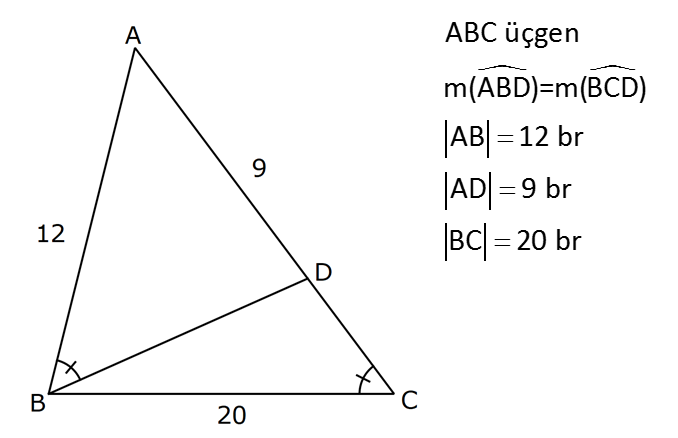
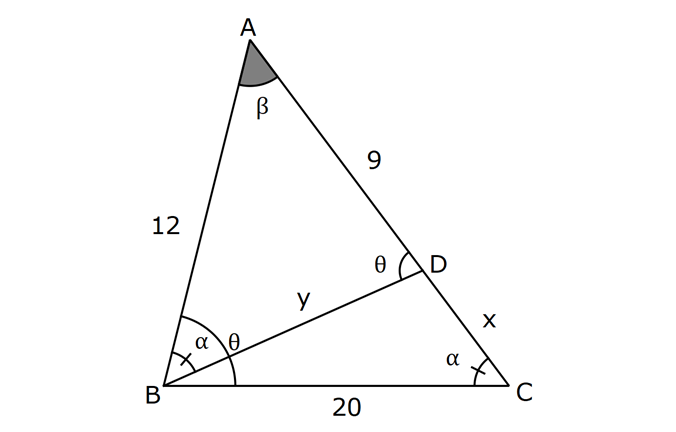
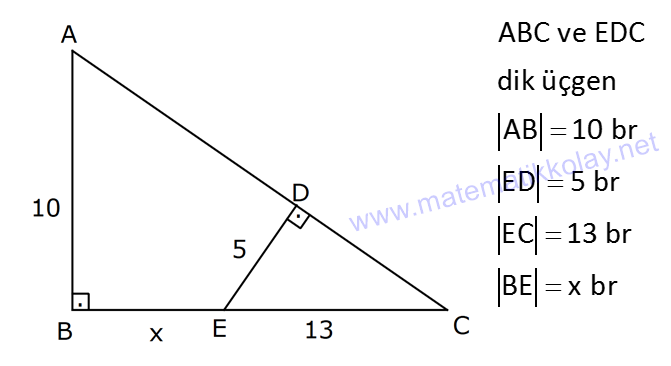
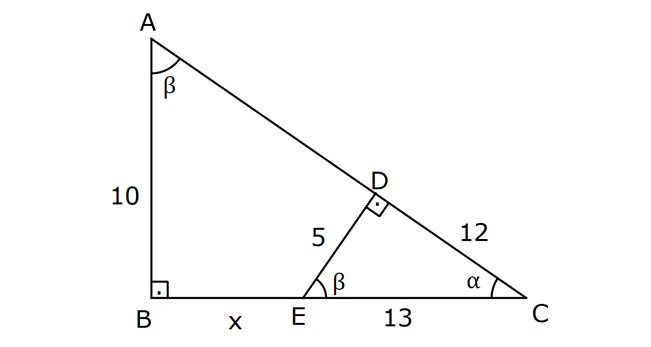
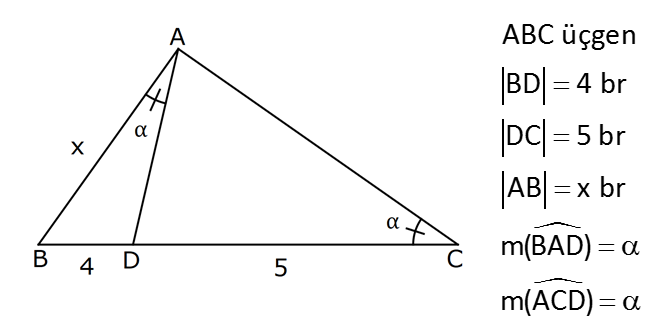
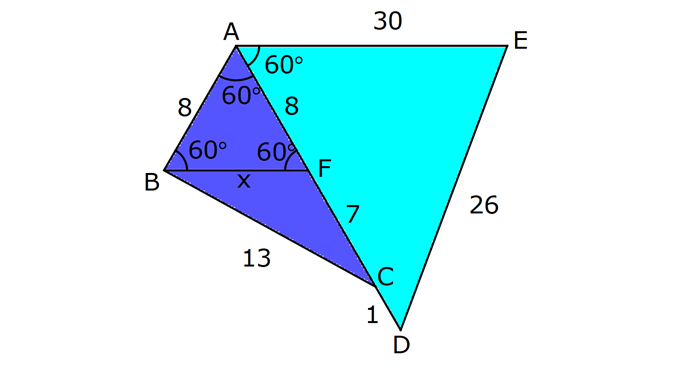
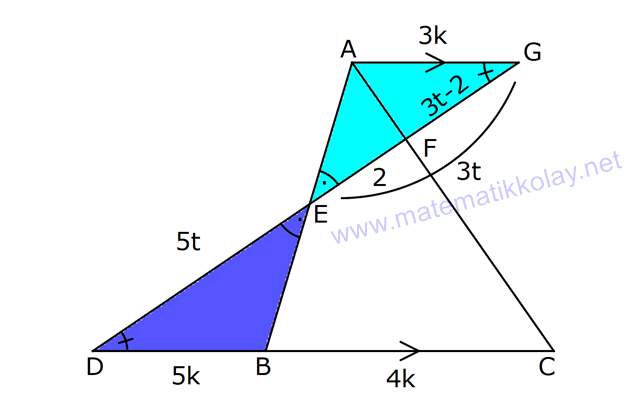
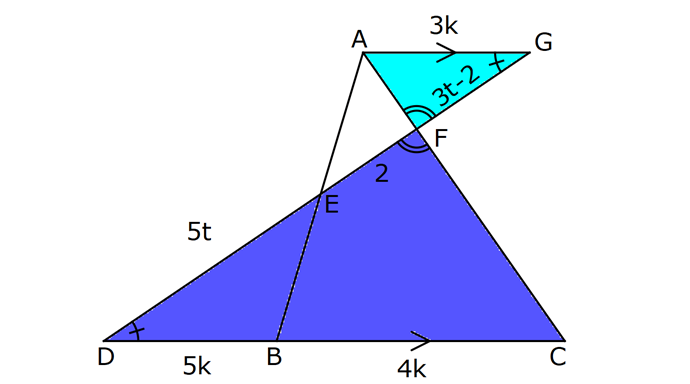
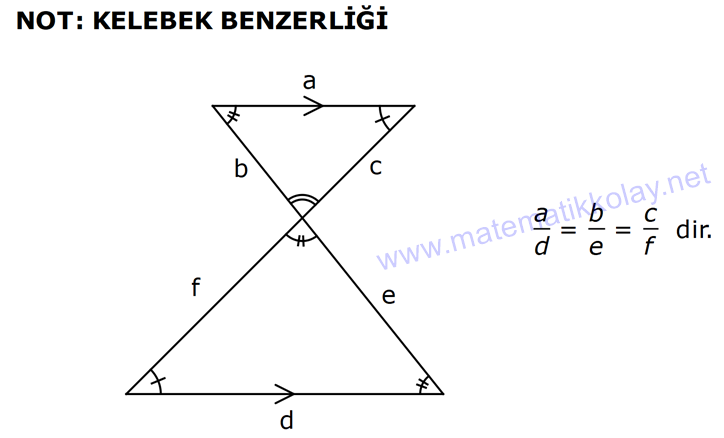
ÜÇGENLERDE BENZERLİK www.matematikkolay.net 1) ABC üçgen DEF eşkenar üçgen ADE FBD AD 8 cm BD 3 cm BF 4 cm AE x cm Yukarıda verilenlere göre x kaç cm dir? A) 8 B) 10 C) 12 D) 15 E) 20 ÇÖZÜM: a x 8 3 ADE FBD ADE üçgeni ile FBD üçgeni benzerdir. Benzer üçgenlerin açıları eşittir ve kenarlar arasında bir oran vardır (k : benzerlik oranı) Açıların karşısındaki kenarları yazıp oranlayalım. ADE F a 4 a x 8 BD 3:00 ÖÖ 4 2 6 k k 2 dir. a 2 a 6 dır. 3 x x 2 2 x 12 cm dir. Cevap : C a 6 2) ABC üçgen m(ABD)=m(BCD) AB 12 br AD 9 br BC 20 br Yukarıda verilenlere göre, BDC üçgeninin çevresi kaç br dir? A) 28 B) 30 C) 33 D) 37 E) 42 ÇÖZÜM: m(ABD) m(BCD) olsun. A açısı olsun. ABD üçgeni ile ACB üçgenine dikkat edelim. İki üçgenin de açıları aynı , , Dolayısıyla bu iki üçgen benzerdir. (Açı- Açı- Açı Benzerlik Teoremi ( )) Kenarları A.A.A. nın karşısı nın karşısı nın karşısı arasındaki oran da eşittir. ABD 9 y 12 ACB 12 20 9 x 9 y 12y 180 y 15 tir. 12 20 9 12 81 9x 144 9x 63 x 7 dir. 12 9 x Ç(BCD) 7 15 20 42 br dir. Cevap: E www.matematikkolay.net 3) ABC ve EDC dik üçgen AB 10 br ED 5 br EC 13 br BE x br Yukarıda verilenlere göre, x kaç br dir? A) 8 B) 11 C) 12 D) 14 E) 16 ÇÖZÜM: EDC üçgeni bir 5-12 -13 üçgenidir. DC 12 br m(ACB) , m(BAC) olsun. 90 dir. m(DEC) olur. ABC üçgeni ile EDC üçgenine dikkat edelim. İki üçgenin de açıları aynı , , 90 Dolayısıyla bu iki üçgen nın karşısı nın karşısı benzerdir.( ) Kenarları arasındaki oran da eşittir. EDC 5 12 ABC 10 13 x 5 A.A.A. 10 2 12 13 x 24 x 11 br dir. 13 x Cevap : B 4) ABC üçgen BD 4 br DC 5 br AB x br m(BAD) m(ACD) Yukarıda verilenlere göre, x kaç br dir? A) 4 B) 5 C) 6 D) 8 E) 9 ÇÖZÜM: nın karşısı nın karşısı 2 ABC üçgeni ile DBA üçgeni benzerdir. ( ) ABC x 9 DBA 4 x x 36 x 6 dır. Cevap: C A.A.A 5) CD AB BF AC AD 6 br AF 4 br FC 11 br BD x br Yukarıda verilenlere göre, x kaç br dir? A) 4 B) 5 C) 6 D) 8 E) 9 www.matematikkolay.net ÇÖZÜM: nın karş Şekildeki gibi E açısına diyelim. B ve C açıları eşit açılar olur. Bunalara da diyelim. A açısı olur. Çünkü 90 dir. ABF üçgeni ile ACD üçgeni benzerdir. ( ) ABF 4 ACD 6 A.A.A 90 nin karşısı ısı 6 x 4 11 4 6 x 60 36 6x 24 6x x 4 br dir. 6 15 Cevap : A 6) ABC üçgen DECF kare AF 4 br BE 8 br Yukarıda verilenlere göre, DECF karesinin çevresi kaç br dir? A) 8 B) 8 2 C) 16 D) 16 2 E) 32 ÇÖZÜM: nın karşısı nın karşısı 2 Karenin bir kenarına x diyelim. Açıları yerleştirdiğimizde ADF üçgeni ile DBE üçgeninin benzer olduğunu görürüz. ( ) ADF 4 x DBE x 8 x 32 x 4 2 dir. Ç(DECF) 4.4 2 16 2 br A.A.A. dir. Cevap : D 7) ABC ve DCF üçgen AB // EC DE // BC BC 15 br DE 9 br EC 6 br AD x br m(ABC) m(CDE) olduğuna göre x kaç br dir? A) 5 B) 4 C) 3 D) 2 E) 1 ÇÖZÜM: www.matematikkolay.net m(ABC) m(CDE) olsun. m(DCE) olur. (İç ters açı) m(BAC) olsun. 2 180 dir (ABC üçgeni iç açıları toplamı) m(DCE) olur. (İç ters açı) DEC üçgeni iç açıları D C E 180 E açısı ya eşittir. nın karşısı nın karşısı 2 180 idi. Dolayısıyla DC 6 br dir. ABC üçgeni ile CDE üçgeni benzer olduğuna göre, ABC 6 x 15 CDE 6 9 6 x 6 2 15 5 9 3 6 x 10 x 4 br dir. Cevap : B 8) ABCD dörtgen AD // BC AB 5 br AC 6 br AD 18 br BC 2 br CD x br Yukarıda verilenlere göre, x kaç br dir? A) 10 B) 11 C) 12 D) 14 E) 15 ÇÖZÜM: m(ACB) m(DAC) dir. (İç ters açı) ACB açısını oluşturan kenarlar 6 ve 2 br DAC açısını oluşturan kenarlar 18 ve 6 br 6 2 ve m(ACB) m(DAC) olduğundan bu iki 18 6 üçgen benzerdir. (Kenar – Açı – Kenar Benzerliği ( .)) Dolayısıyla diğer kenarlar arasında da aynı oran vardır. 6 2 2 2x 30 x 15 br dir. 18 6 6 Cev K.A.K 5 5 x x ap: E 9) ABC, AED üçgen m(EAD)=60 AB AF 8 br BC 13 br FC 7 br CD 1 br AE 30 br ED 26 br Yukarıda verilenlere göre, x kaç br dir? A) 8 B) 9 C) 10 D) 11 E) 12 ÇÖZÜM: www.matematikkolay.net CAB üçgeninin kenarları 8, 13, 15 EAD üçgeninin kenarları 16, 26, 30 dur. İki üçgenin kenarları arasında sabit bir oran var.(1 / 2) Dolayısıyla bu iki üçgen benzerdir. (Kenar -Kenar -Kenar Benzerliği ( K. 60 60 olur. )) E A D C A B olduğundan açılar da aynıdır. ABF üçgeni ikizkenar bir üçgendi. A açısı 60 ise, diğer iç açıları da 60 dir. Yani bir eşkenar üçgendir. Bu sebeple x 8 br dir. Cevap : A K.K. 10) ABC üçgen, AG // DC AG DB BC ve EF 2 br olduğuna göre, 3 5 4 DG uzunluğu kaç br dir? A) 14 B) 16 C) 18 D) 22 E) 24 ÇÖZÜM: AG DB BC k olsun. 3 5 4 AG 3k, DB 5k ve BC 4k olur. AG // DC olduğu için EDB üçgeni ile EGA üçgeni arasında kelebek benzerliği vardır. ( ) A.A.A EDB 3k ED EGA EG 5 k ED 5t, EG 3t diyelim. FG 3t 2 kalır. Daha sonra AFG üçgeni ile CFD üçgeni arasında kelebek benzerliği yapalım. AFG 3t 2 3k CFD 5t 2 9k 3 2 9t 6 5t 2 4t 8 t 2 dir. DG 5t 3t 8t 16 br dir. Cevap: B
