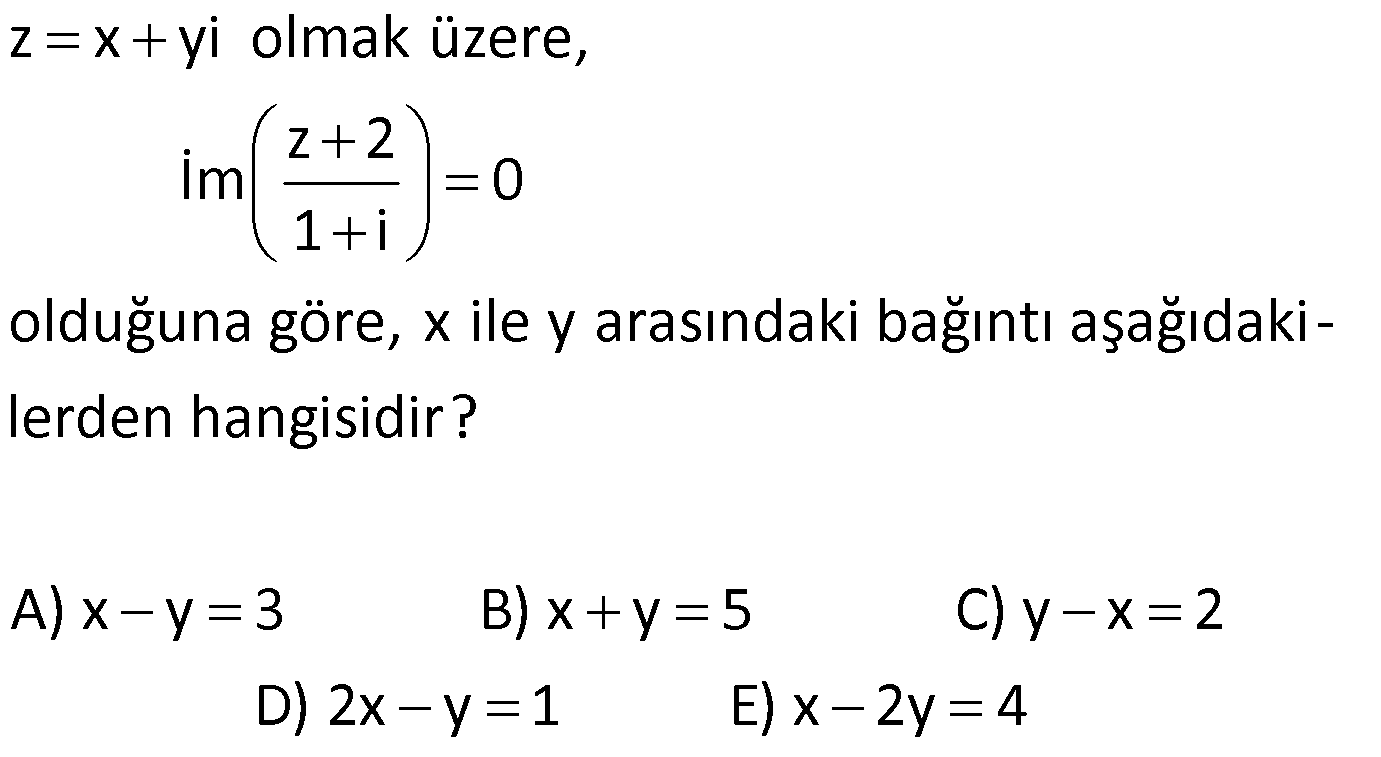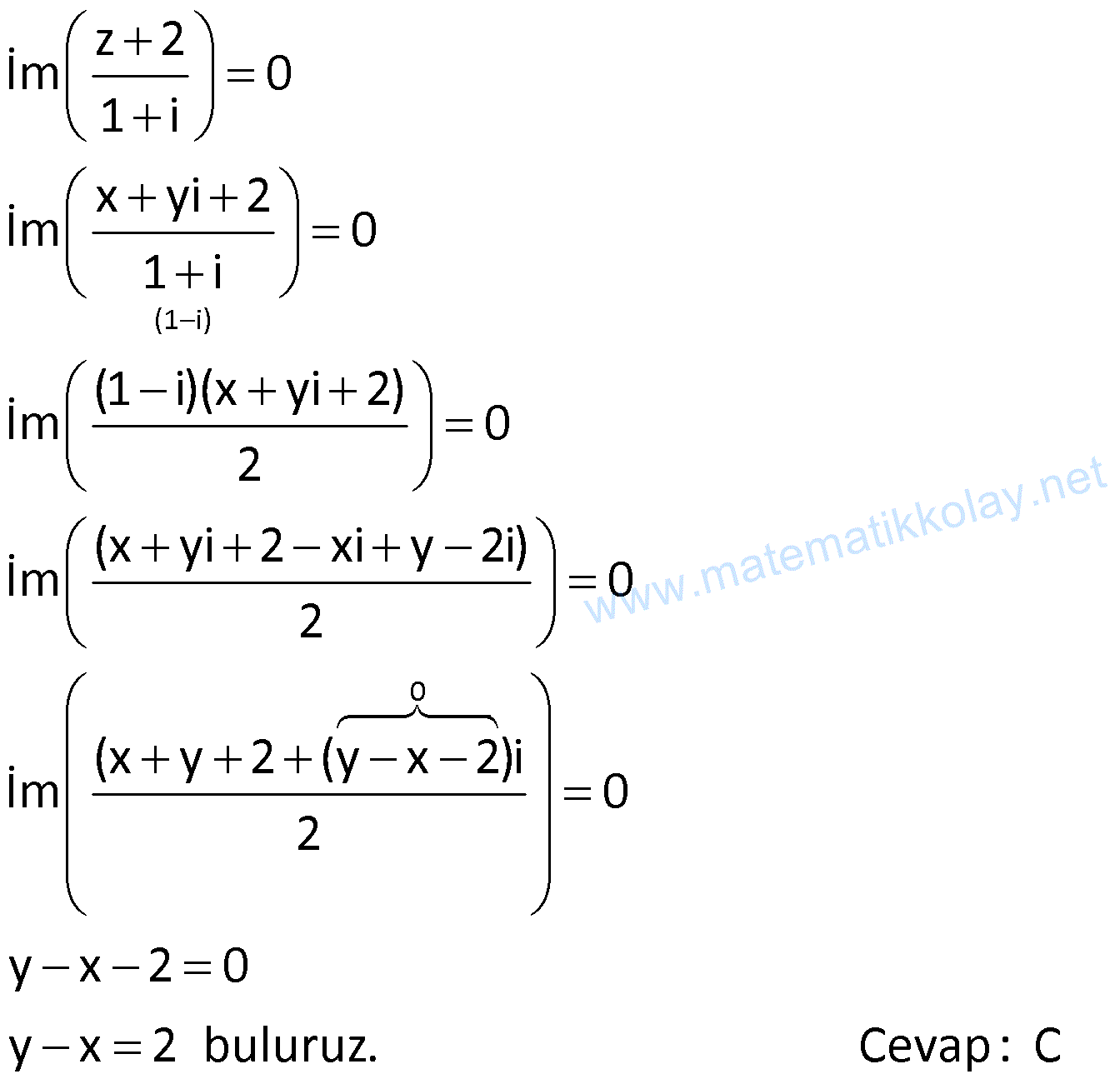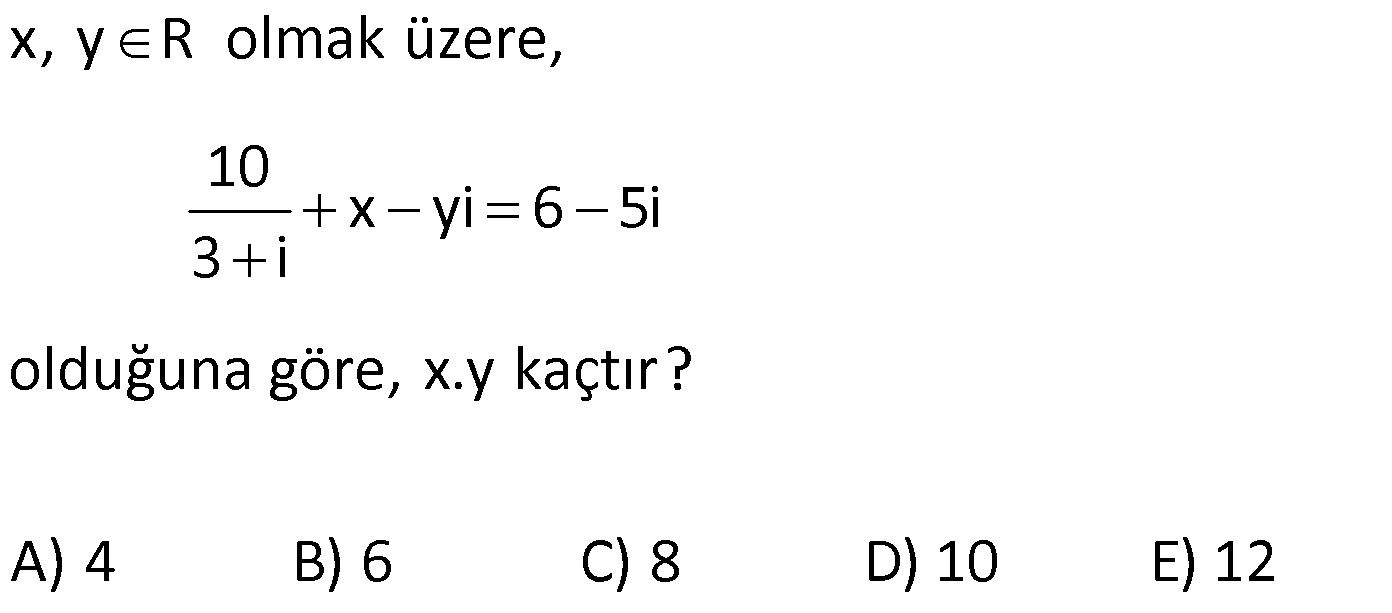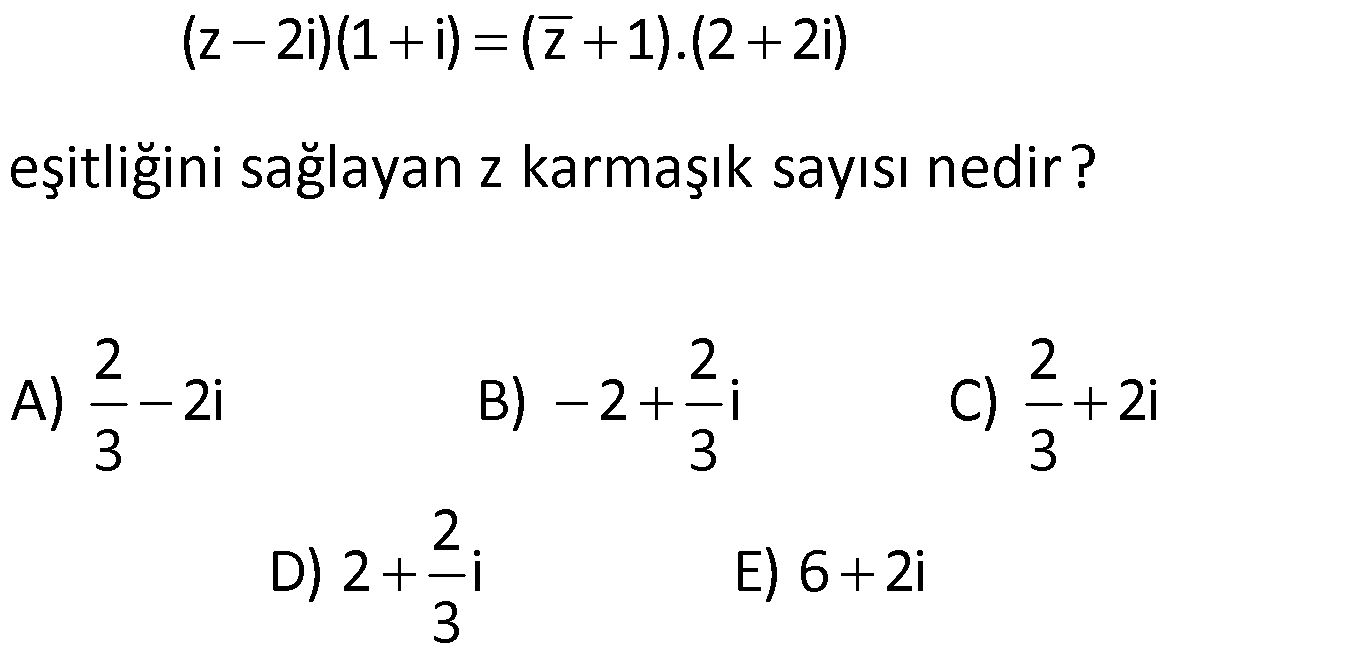Soru Sor sayfası kullanılarak Karmaşık Sayılar konusu altında Karmaşık Sayıların Eşitliği, Karmaşık Sayıların 0’a eşit olması ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Eğer sorular ya da çözümler konusunda bir problem görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
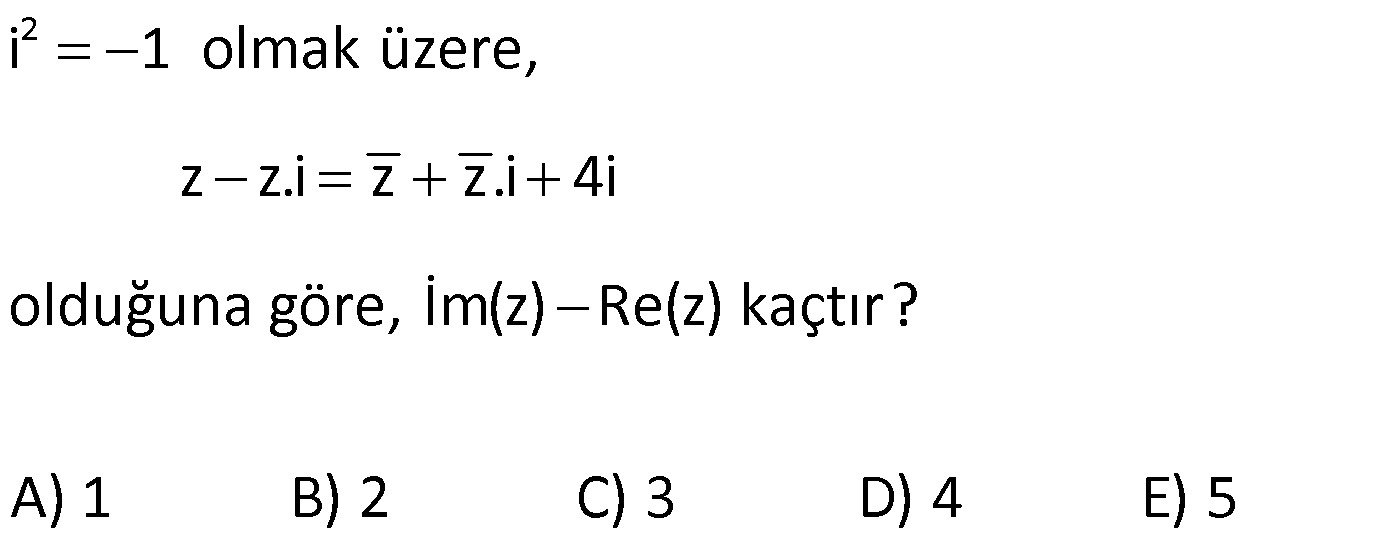
KARMAŞIK SAYILARIN EŞİTLİĞİ www.matematikkolay.net 1) z x yi olmak üzere, z 2 İm 0 1 i olduğuna göre, x ile y arasındaki bağıntı aşağıdaki – lerden hangisidir? A) x y 3 B) x y 5 C) y x 2 D) 2x y 1 E) x 2y 4 ÇÖZÜM: (1 i) 0 z 2 İm 0 1 i x yi 2 İm 0 1 i (1 i)(x yi 2) İm 0 2 (x yi 2 xi y 2i) İm 0 2 (x y 2 (y x 2)i İm 0 2 y x 2 0 y x 2 buluruz. Cevap: C 2) 2 1 i 1 olmak üzere, 1 z x i 5 ve Re (z) 6 olduğuna göre, x in alabileceği değerlerin çarpımı kaçtır? A) 2 B) 3 C) 4 D) 5 E) 6 ÇÖZÜM: 1 2 (x i 5) 2 2 2 2 z x i 5 z x i 5 1 x i 5 (z) x i 5 x 5 x Bu ifadenin reel kısmı tir. x 5 x 1 6x x 5 x 5 6 0 x 6x 5 c 5 köklerinin çarpımı 5 buluruz. Cevap : D a 1 3) 2 1 2 1 2 i 1 olmak üzere, z a 2 (b 2)i z 3 6i z z olduğuna göre, a b toplamı kaçtır? A) 4 B) 8 C) 9 D) 12 E) 16 ÇÖZÜM: Reel kısımlar birbirine, İmajiner kısımlar da birbirine eşit olmalıdır. Buna göre; a 2 3 a 1 b 2 6 b 8 buluruz. Toplamları a b 1 8 9 buluruz. Cevap : C 4) 1 2 1 2 a ve b reel sayılar olmak üzere, z 3 4i z (a 1) bi z z olduğuna göre, a.b çarpımı kaçtır? A) 6 B) 10 C) 12 D) 16 E) 20 www.matematikkolay.net ÇÖZÜM: 1 1 2 z 3 4i dir. z z ise; Reel kısımlar birbirine, İmajiner kısımlar da birbirine eşit olmalıdır. Buna göre; a 1 3 a 4 b 4 tür. a.b 4.( 4) 16 buluruz. Cevap: E 5) 2 a ve b reel sayılar olmak üzere, 2x ax b i 0 denkleminin çözüm kümesi 2 i, m ni olduğuna göre, a b kaçtır? A) 6 B) 9 C) 12 D) 15 E) 18 ÇÖZÜM: 2 2 0 0 7 2 i , bu denklemin bir kökü ise; denklemde yerine yazalım. 2x ax b i 0 2.(2 i) a(2 i) b i 0 2.(3 4i) 2a ai b i 0 6 8i 2a ai b i 0 (6 2a b) i(a 7) 0 a 7 dir. 6 2a b 0 b 8 dir. Toplamları 7 8 15 buluruz. Cevap: D 6) 2 2 2 i 1 olmak üzere, z i.z 2 2 z 4 eşitliğini sağlayan z karmaşık sayısı aşağıdakilerden hangisidir? A) 1 2i B) 1 3i C) 2 3i D) 4i E) 3i ÇÖZÜM: 2 2 2 2 2 2 2 2 2 6 olmalı 0 olmalı 2 2 2 z i.z 2 2z 8 z i.z 6 z iz 6 z a bi olsun. (a bi) i.(a bi) 6 a 2abi b ai b 6 a b b i(2ab a) 6 2ab a 0 a(2b 1) 0 a 0 seçelim. a b b 6 0 b b 2 2 2 6 b b 6 b b 6 b b 6 0 (b 3)(b 2) 0 b 3 b 2 dir. a bi 0 3i veya 0 2i dir. Ancak z 2i , paydayı 0 yapar. Bu sebeple; z 3i dir. Cev ap: E 7) 2 i 1 ve a, b R olmak üzere, 2a 1 3i bi b 1 2ai i eşitliğini sağlayan a b kaçtır? 1 3 5 A) B) 1 C) D) 2 E) 2 2 2 ÇÖZÜM: 2a 1 3i bi b 1 2ai i 2a 1 i(3 b) b 1 i(2a 1) reel kısımlar birbirine, imajiner kısımlar da birbirine eşit olmalıdır. 2a 1 b 1 2a b 2 dir. 3 b 2a 1 2a b 4 tür. 3 4a 6 a dir. 2 3 2a b 4 2 b 1 b 1 dir. 2 3 1 a b 1 buluruz. Cevap: A 2 2 8) www.matematikkolay.net 2 i 1 ve x, y R olmak üzere, x 2 iy 2i x 6 eşitliğini sağlayan x.y çarpımı kaçtır? A) 4 B) 2 C) 0 D) 2 E) 4 ÇÖZÜM: x 2 iy 2i x 6 reel kısımlar birbirine, imajiner kısımlar da birbirine eşit olmalıdır. x 2 x 6 2x 4 x 2 dir. y 2 y 2 dir. x.y 2.( 2) 4 buluruz. Cevap: E 9) 2 i 1 olmak üzere, z 3 i z.i eşitliğini sağlayan z karmaşık sayısı için z.z kaçtır? A) 1 B) 3 C) 5 D) 7 E) 9 ÇÖZÜM: 2 2 z a bi olsun. z 3 i z.i a bi 3 i (a bi)i a bi 3 i ai b a 3 b a b 3 tür. ve b 1 a a b 1 dir. 2a 4 a 2 dir. b 1 dir. z 2 i z.z 2 1 4 1 5 buluruz. Ceva p: C 10) x, y R olmak üzere, 10 x yi 6 5i 3 i olduğuna göre, x.y kaçtır? A) 4 B) 6 C) 8 D) 10 E) 12 ÇÖZÜM: (3 i) 10 x yi 6 5i 3 i 10.(3 i) x yi 6 5i 9 1 3 i x yi 6 5i Reel kısımlar birbirine, imajiner kısımlar da birbirine eşit olmalıdır. 3 x 6 x 3 i yi 5i y 4 tür. x.y 3.4 12 buluruz. Cevap: E 11) 2 i 1 olmak üzere, z z.i z z.i 4i olduğuna göre, İm(z) Re(z) kaçtır? A) 1 B) 2 C) 3 D) 4 E) 5 ÇÖZÜM: z a bi olsun. z z.i z z.i 4i a bi (a bi).i a bi (a bi).i 4i a bi ai b a bi ai b 4i a b (b a)i a b i(a b 4) İmajiner kısımlar birbirine eşit olmalıdır. b a a b 4 2b 2a 4 b a 2 buluruz. Cevap: B 12) www.matematikkolay.net 2 (z i)(2 i) z 1 eşitliğini sağlayan z karmaşık sayısı aşağıdakilerden hangisine eşit olabilir? A) 2 2i B) 2 i C) 1 i D) 1 i E) 2 i ÇÖZÜM: 2 2 2 2 2 2 z a bi diyerek çözmek, uzun zaman alabilir. Bu soruda başka bir pratik yol var, onu kullanalım. z 1 ifadesini z i olarak ifade edebiliriz. O halde; z i 2 i z 1 z i 2 i z i olur. z i 2 i z i z i z i olabilir. z i 2 i z i z i z i değilse, sadeleştirebiliriz. 2 i z i 2 2i z buluruz. Cevap: A 13) (z 2i)(1 i) (z 1).(2 2i) eşitliğini sağlayan z karmaşık sayısı nedir? 2 2 2 A) 2i B) 2 i C) 2i 3 3 3 2 D) 2 i E) 6 2i 3 ÇÖZÜM: z 2i 1i z 1.2. 1i z 2i 2z 2 z a bi olsun. z a bi olur. a bi 2i 2 a bi 2 a bi 2i 2a 2bi 2 a 3bi 2 2i a 2 olmalı 2 3b 2 b olmalıdır. 3 2 z a bi 2 i buluruz. Cevap: B 3