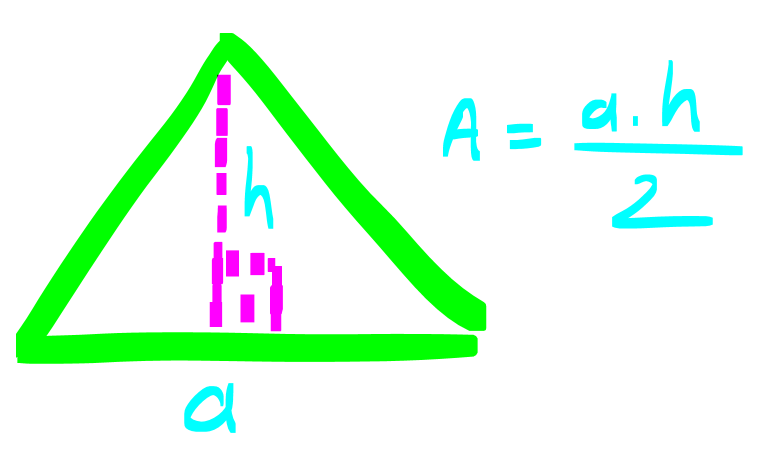 Bu bölümde Üçgenin Alanı ile ilgili 29 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…
Bu bölümde Üçgenin Alanı ile ilgili 29 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…
Eğer sorular ya da çözümler konusunda bir problem görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.
Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)
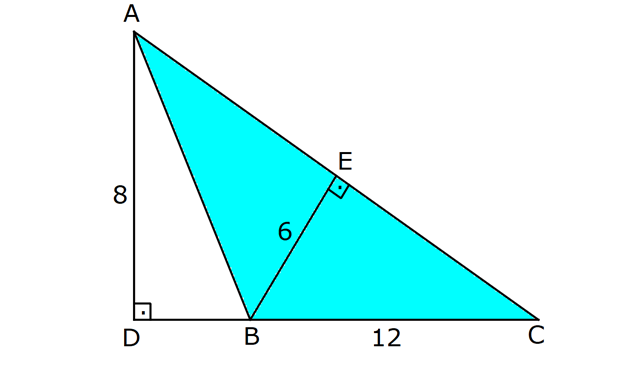
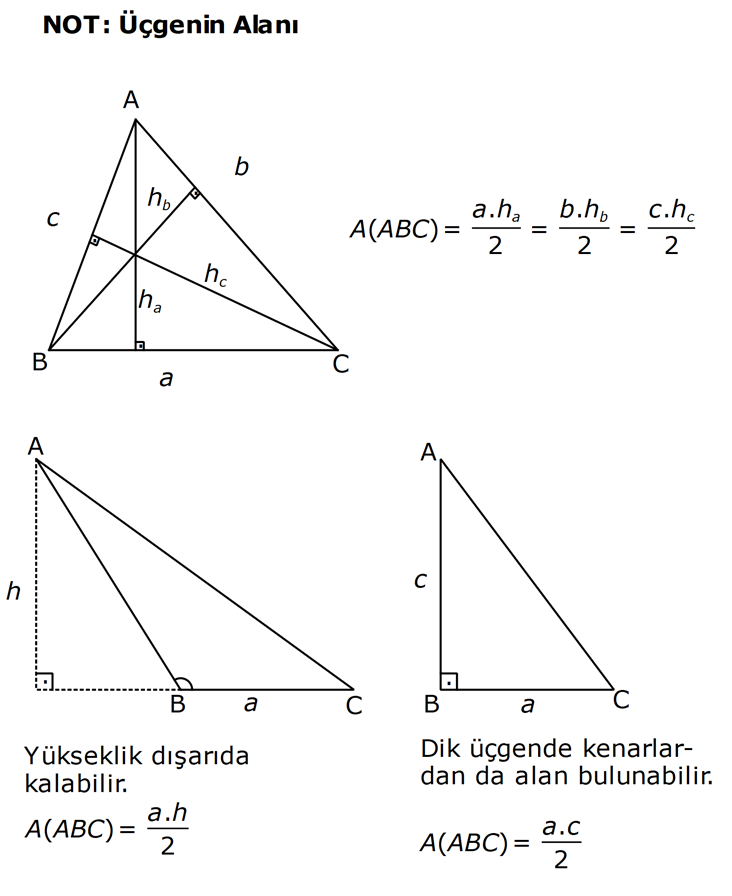
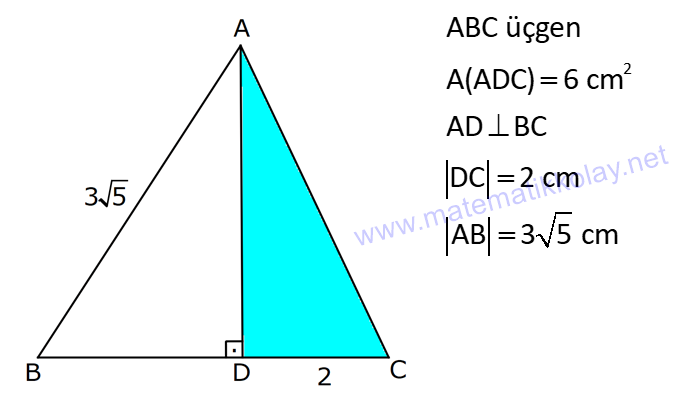
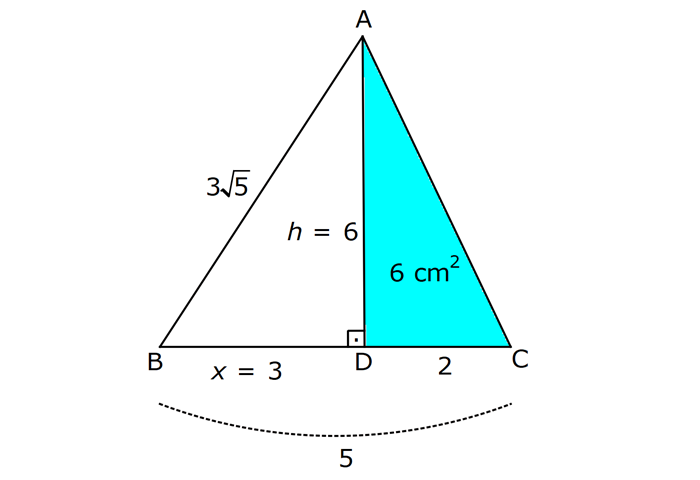
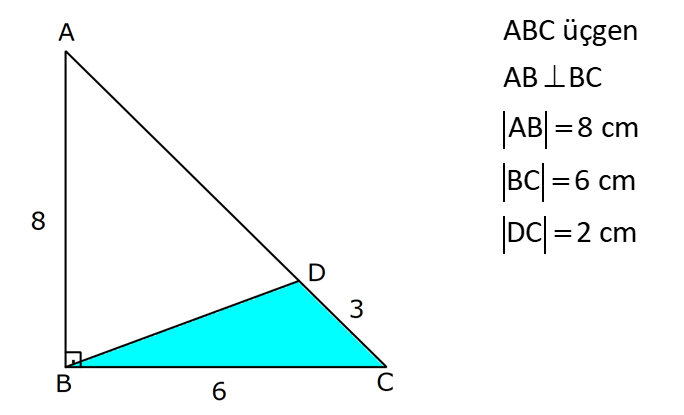
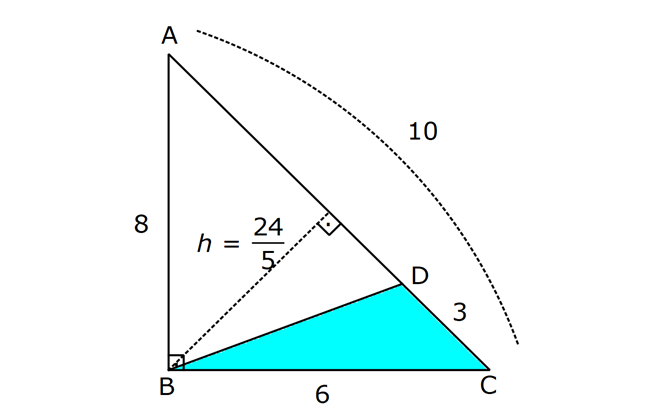
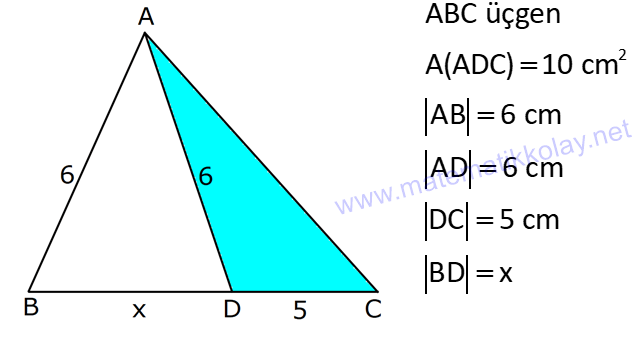
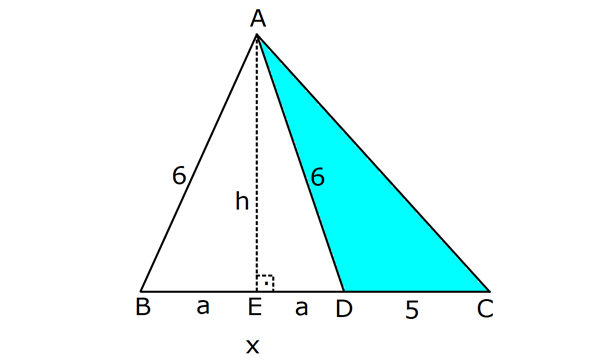
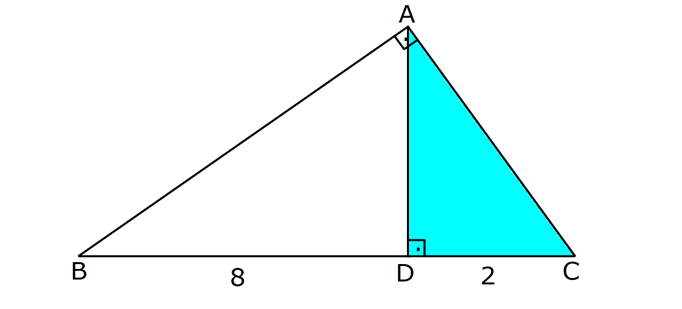
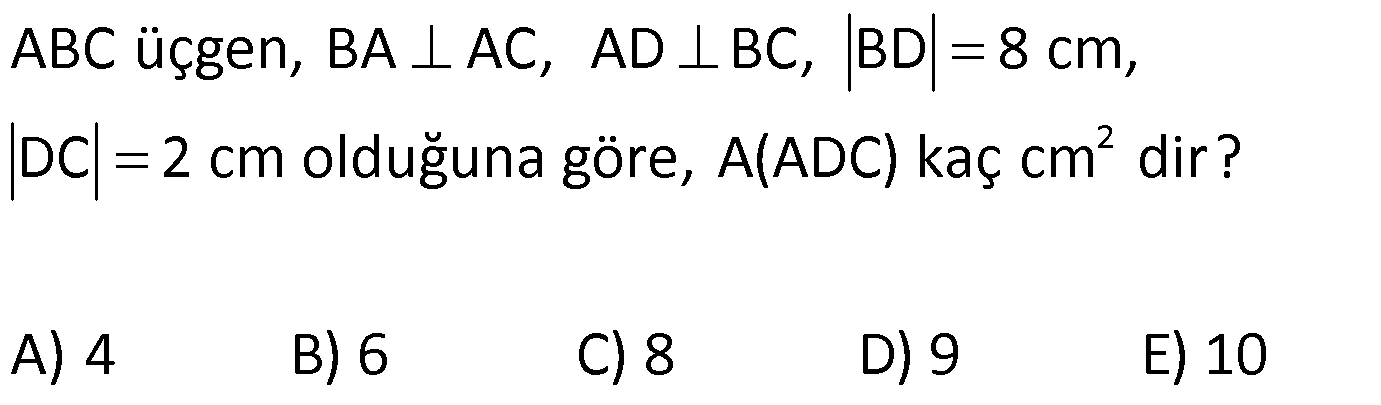
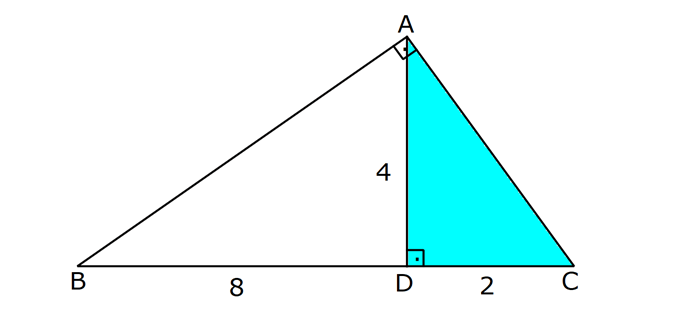
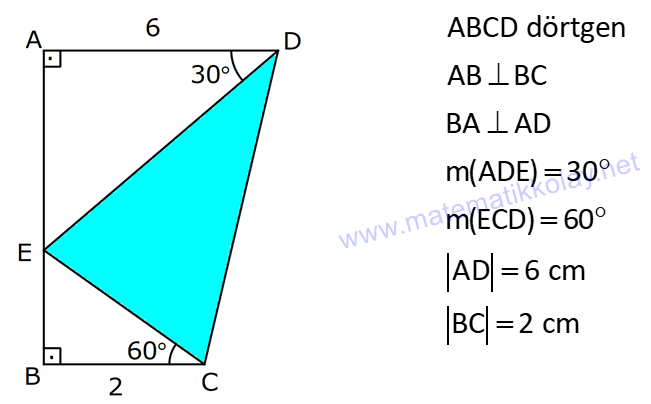
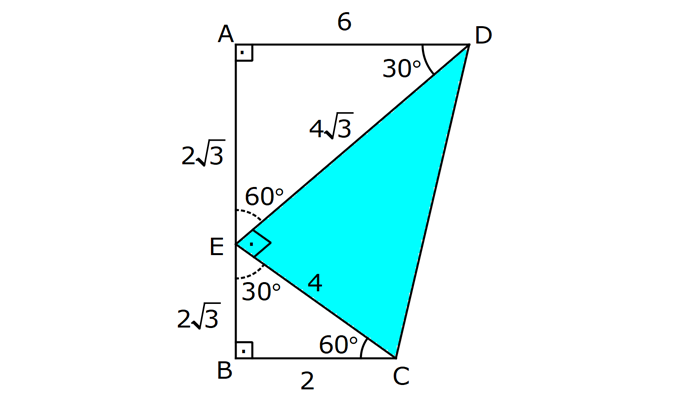
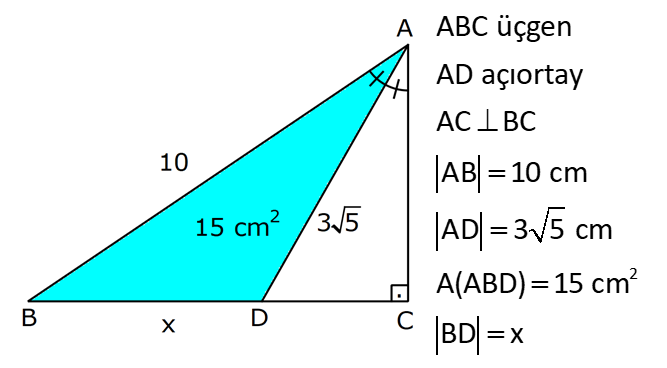
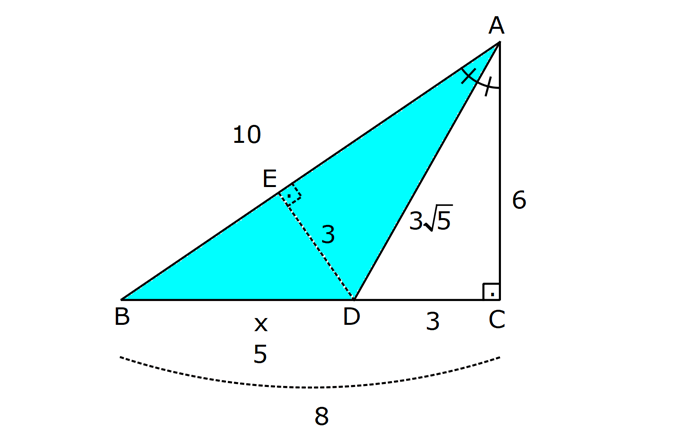
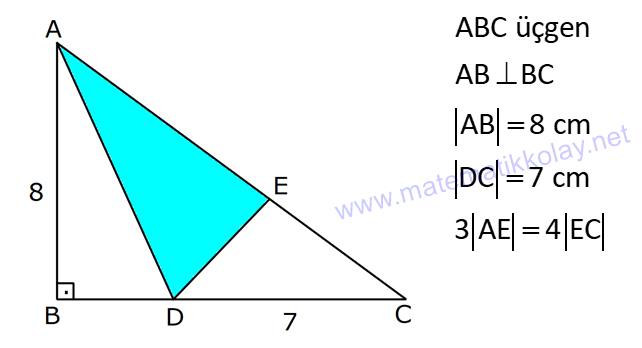
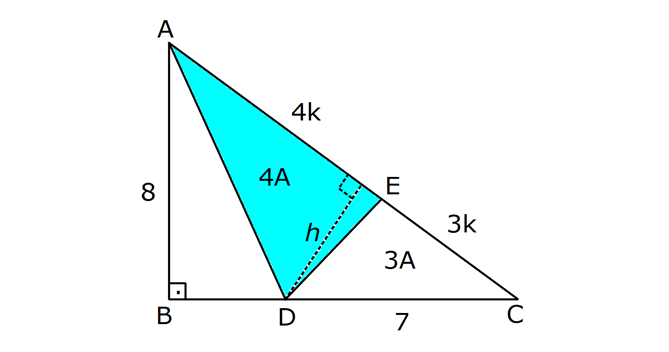
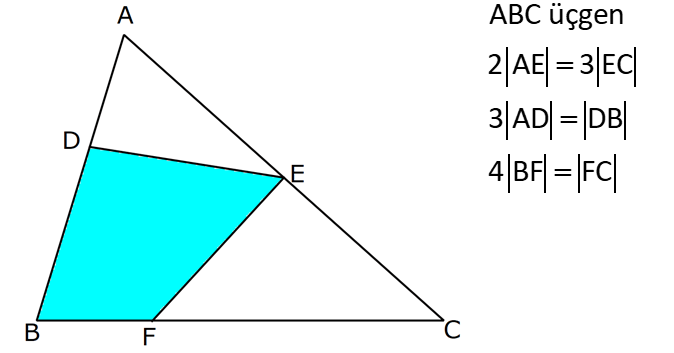
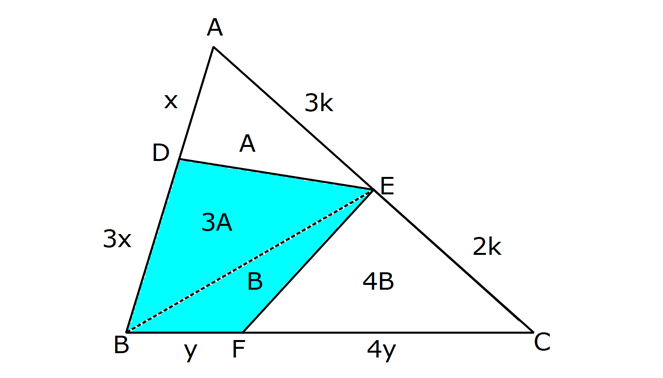
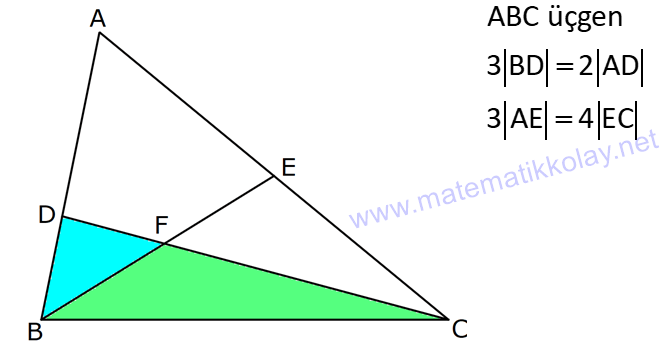
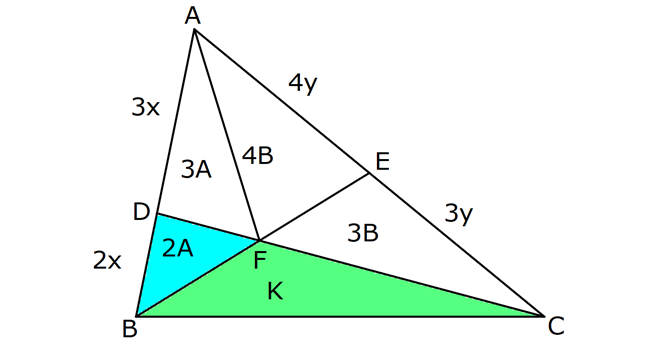
ÜÇGENİN ALANI www.matematikkolay.net 1) ADC üçgen AD DC BE AC AD 8 cm BE 6 cm BC 12 cm Yukarıda verilenlere AC kaç cm dir? A) 16 B) 18 C) 20 D) 24 E) 28 ÇÖZÜM: 2 ABC üçgeninin alanını bulabiliriz. BC ve buna ait yüksekliği kullanırsak, 12.8 A(ABC) 48 cm dir. 2 AC uzunluğu ve buna ait yüksekliği kullandığı- mızda da aynı sonuç gelmelidir. AC .6 48 AC 16 c 2 m dir. Cevap : A 2) 2 ABC üçgen A(ADC) 6 cm AD BC DC 2 cm AB 3 5 cm 2 Yukarıda verilenlere göre, A(ABC) kaç cm dir? A) 9 B) 12 C) 15 D) 18 E) 21 ÇÖZÜM: www.matematikkolay.net 2 6 .h 2 2 2 2 2 2 2 h 6 cm dir. ABD üçgeninde pisagordan, x 6 3 5 x 36 45 x 9 x 3 cm dir. BC 3 2 5 cm dir. 5.6 30 A(ABC) 15 cm dir. Cevap: C 2 2 3) ABC üçgen AB BC AB 8 cm BC 6 cm DC 2 cm 2 Yukarıda verilenlere göre, A(BDC) kaç cm dir? 15 25 35 36 72 A) B) C) D) E) 4 6 6 5 5 ÇÖZÜM: 2 Dik kenarları kullanarak A(ABC) yi bulabiliriz. 6.8 A(ABC) 24 cm dir. 2 ABC üçgeni 6 – 8 -10 üçgeni olduğundan, AC 10 cm dir. 10 cm’lik kenara ait yükseklik ile de aynı A(ABC) değerini bulmalıyız. 10 5 .h 2 24 24 h cm dir. 5 Bu yükseklik aynı zamanda BDC üçgeninin de bir yüksekliğidir. 24 72 3 5 A(BDC) 2 36 5 2 36 2 cm buluruz. Cevap : D 5 4) 2 ABC üçgen A(ADC) 10 cm AB 6 cm AD 6 cm DC 5 cm BD x Yukarıda verilenlere göre, x kaç cm dir? A) 3 2 B) 8 C) 4 5 D) 5 3 E) 12 ÇÖZÜM: www.matematikkolay.net 5.h A(ADC) 2 10 2 5 2 2 2 2 2 .h h 4 cm dir. 2 ABD üçgeni ikizkenar üçgen olduğundan, yükseklik tabanı iki eş parçaya ayırır. ABE üçgeninde pisagor yapalım. a 4 6 a 16 36 a 20 a 2 5 cm dir. x 2.2 5 4 5 cm di r. Cevap: C 5) 2 ABC üçgen, BA AC, AD BC, BD 8 cm, DC 2 cm olduğuna göre, A(ADC) kaç cm dir? A) 4 B) 6 C) 8 D) 9 E) 10 ÇÖZÜM: 2 Öklid teoremine göre, AD 2.8 AD 4 cm dir. 2 A(ADC) .4 2 2 4 cm dir. Cevap: A 6) ABCD dörtgen AB BC BA AD m(ADE) 30 m(ECD) 60 AD 6 cm BC 2 cm 2 Yukarıda verilenlere göre, A(DEC) kaç cm dir? A) 5 2 B) 6 3 C) 12 D) 8 3 E) 9 2 ÇÖZÜM: www.matematikkolay.net 3 AED üçgeninde 60 nin karşısı 6 cm ise, 6 6 3 30 nin karşısı 2 3 cm dir. 3 3 90 nin karşısı ED 2.2 3 4 3 cm dir. EBC üçgeninde 60 nin karşısı 2 3 cm ise, 30 nin karşısı 2 cm dir. 90 nin karşı 2 sı EC 4 cm dir. DEC açısı 90 olduğundan, 4 3.4 A(DEC) 8 3 cm dir. Cevap: D 2 7) 2 ABC üçgen AD açıortay AC BC AB 10 cm AD 3 5 cm A(ABD) 15 cm BD x Yukarıda verilenlere göre, x kaç cm dir? 7 9 A) 3 B) C) 4 D) E) 5 2 2 ÇÖZÜM: 2 2 2 2 2 10. ED 10. ED A(ABD) 15 ED 3 cm dir. 2 2 Açıortaydan kollara inilen dikmeler birbirine eşit olacağından, DC 3 cm dir. ADC üçgeninde pisagordan, 3 AC 3 5 9 AC 45 AC 36 AC 6 cm dir. ABC üçgeni 6 – 8 -10 üçgeni olur. BC 8 cm dir. x 8 3 5 cm buluruz. Cevap : E 8) ABC üçgen AB BC AB 8 cm DC 7 cm 3 AE 4 EC 2 Yukarıda verilenlere göre, A(ADE) kaç cm dir? A) 9 B) 12 C) 16 D) 18 E) 21 ÇÖZÜM: www.matematikkolay.net 7. 8 A(ADC) 4 2 2 4k 3k 28 cm dir. 3 AE 4 EC AE 4k, EC 3k diyebiliriz. Yükseklikleri aynı olan üçgenlerin alanları oranı, tabanları oranına eşittir. Bu sebeple A(ADE) 4 tür. A(EDC) 3 A(ADE) 4A, A(EDC) 3 Not : 2 2 4 A diyebiliriz. 4A 3A 28 ise 7A 28 A 4 cm dir. A(ADE) 4 A 4.4 16 cm dir. Cevap: C 9) ABC üçgen 2 AE 3 EC 3 AD DB 4 BF FC 2 2 A(ABC) 100 cm olduğuna göre, A(BDEF) kaç cm dir? A) 45 B) 53 C) 58 D) 65 E) 75 ÇÖZÜM: ABE üçgeni ile EBC üçgeninin alanları oranı AE ile EC arasındaki orana eşittir. A(ABE) 3k A(EBC) 2 k 2 2 20 A(ABE) 3K, A(EBC) 2K şeklindedir. 3K 2K 100 5K 100 K 20 cm dir. A(ABE) 3K 60 cm olur. Şimdi burdan A(BDE)’yi bulalım. BDE üçgeni ile ADE üçgeninin alanları oranı, A(BDE) 3 x A(ADE) x 2 15 2 20 3A şeklindedir. A 4A 60 A 15 A(BDE) 3A 45 cm dir. Diğer kısmı da bulalım. A(EBC) 2K 40 cm dir. A(BEF) y A(EFC) 4 y 2 2 B şeklindedir. 4B 5B 40 B 8 cm dir. A(BDEF) 45 8 53 cm buluruz. Cevap: B 10) ABC üçgen 3 BD 2 AD 3 AE 4 EC A(BDF) Yukarıda verilenlere göre, oranı kaçtır? A(BFC) 2 7 8 6 9 A) B) C) D) E) 3 22 15 17 14 ÇÖZÜM: www.matematikkolay.net [AF] doğru parçasını çizelim. Kenarların oranından yararlanarak, A(ADF) 3A, A(BDF) 2A ve A(AFE) 4B, A(EFC) 3B diyebiliriz. ABE üçgeninin alanı ile EBC üçgeninin alanı arasınAE 4 y daki oran da EC 3 y 4 e eşittir. 3 5A 4B 4 15A 12B K 3B 3 4K 12B 15A K tür. 4 O halde, A(BDF) 2 A A(BFC) 15 A 8 tir. Cevap : C 15 4
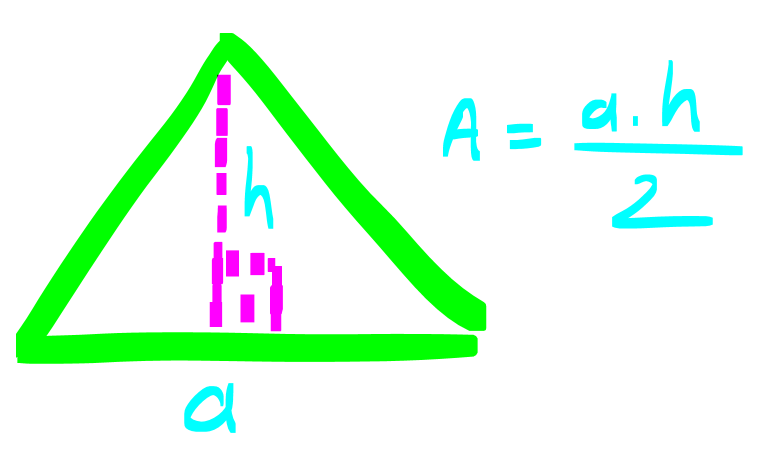 Bu bölümde Üçgenin Alanı ile ilgili 29 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…
Bu bölümde Üçgenin Alanı ile ilgili 29 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar… 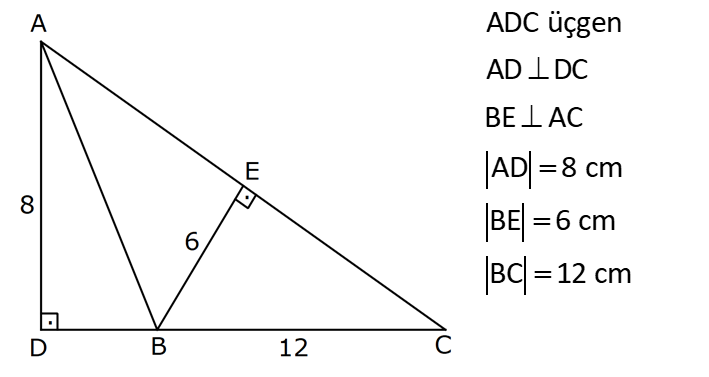
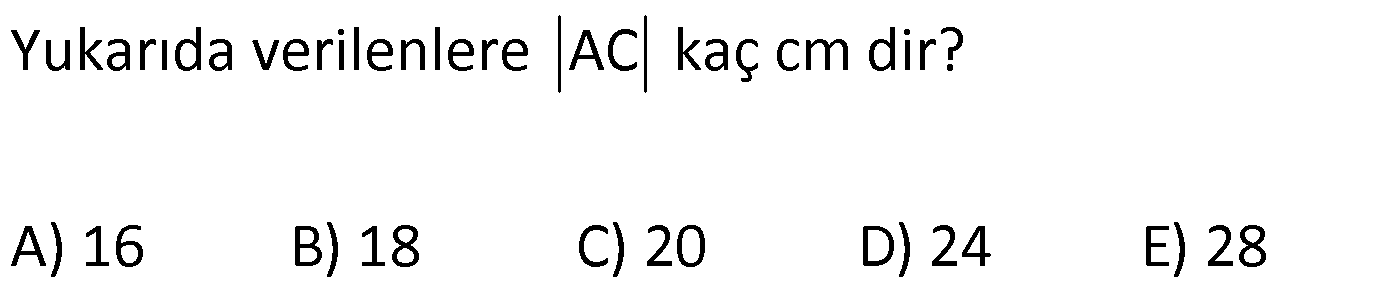


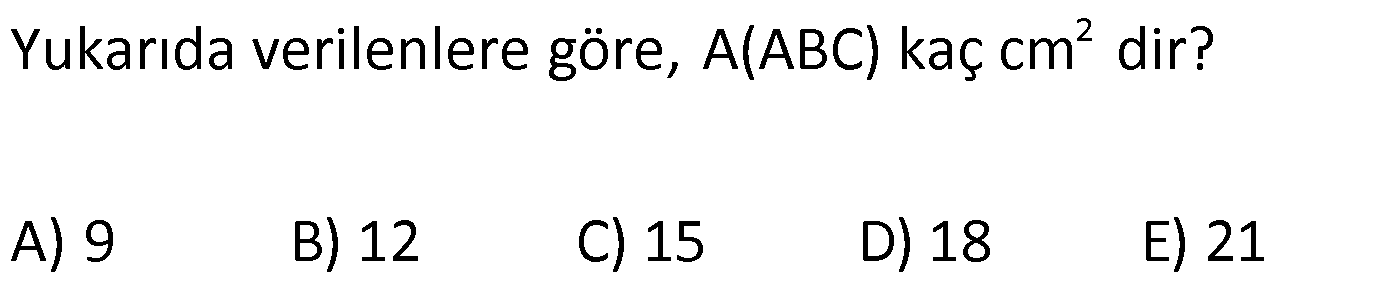
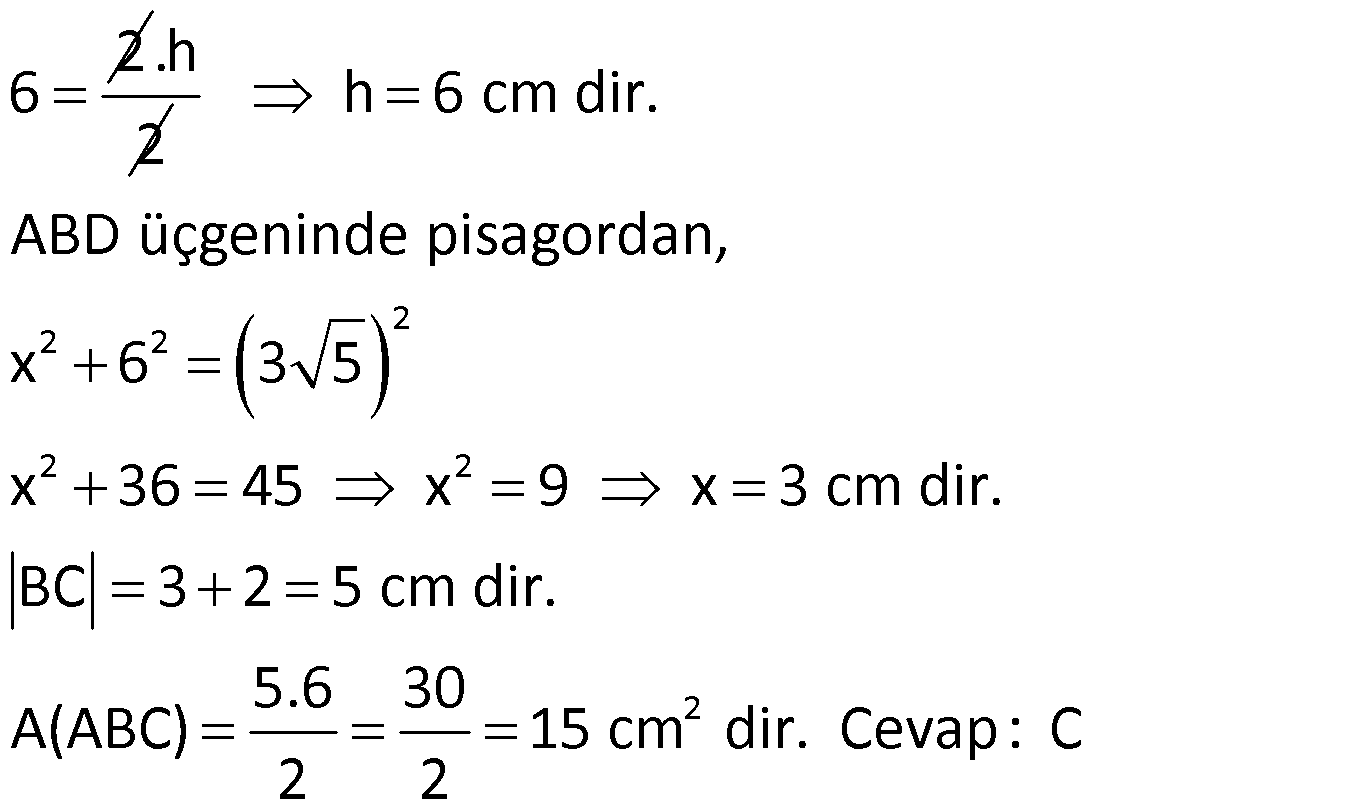
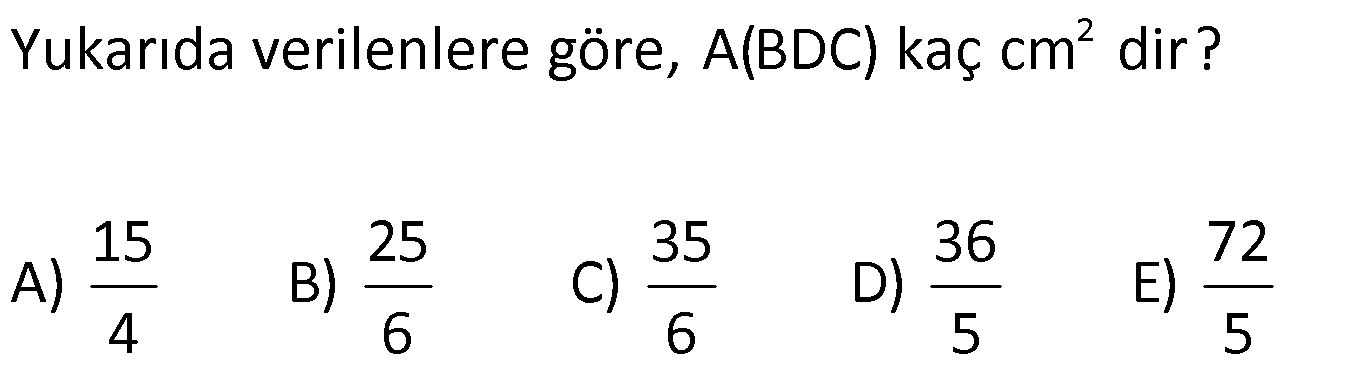

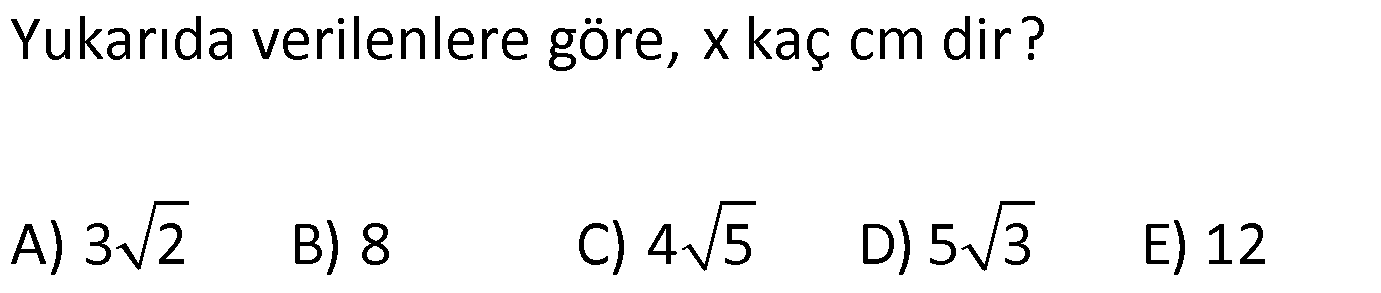


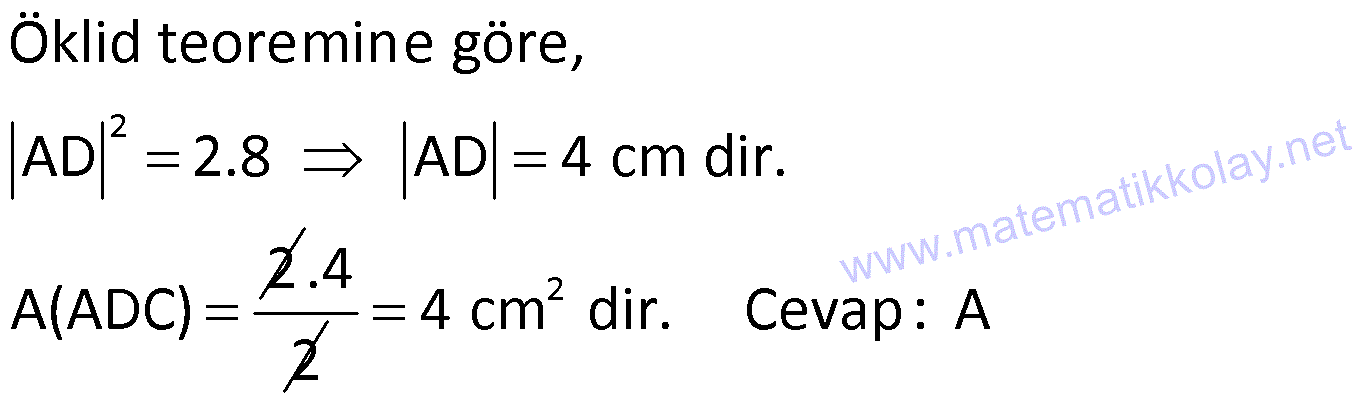

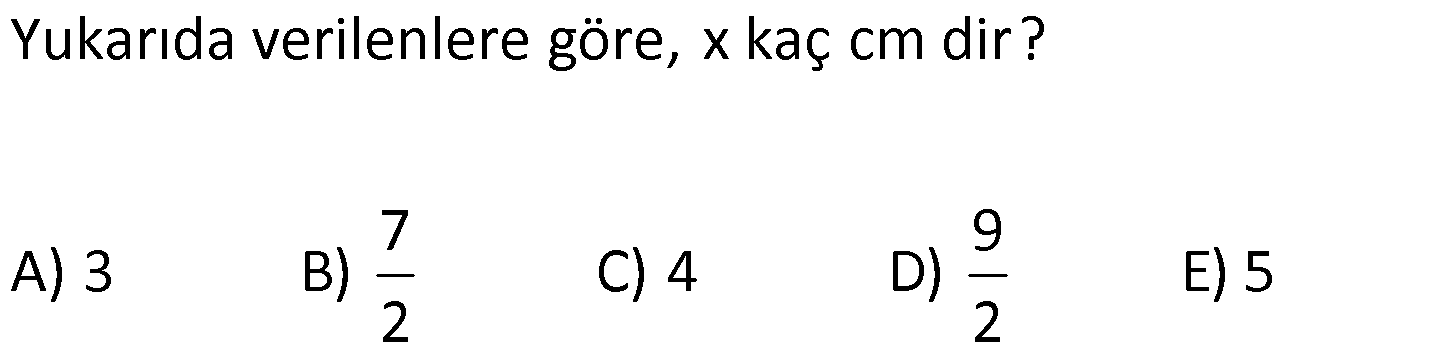

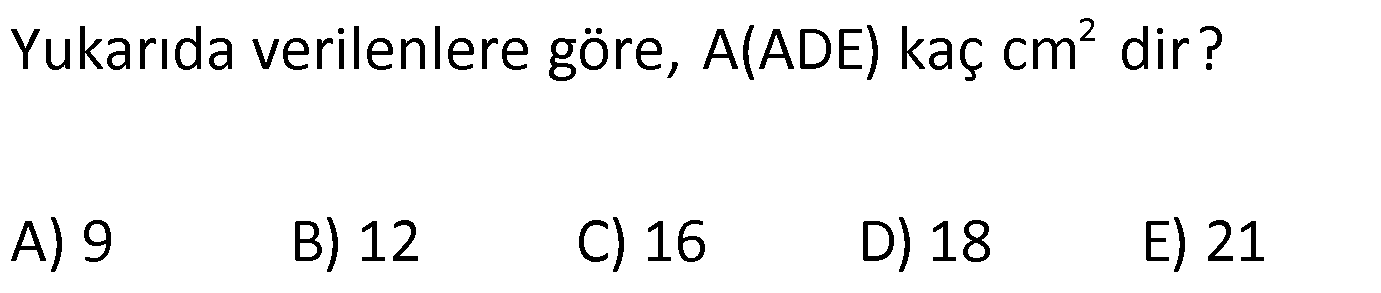

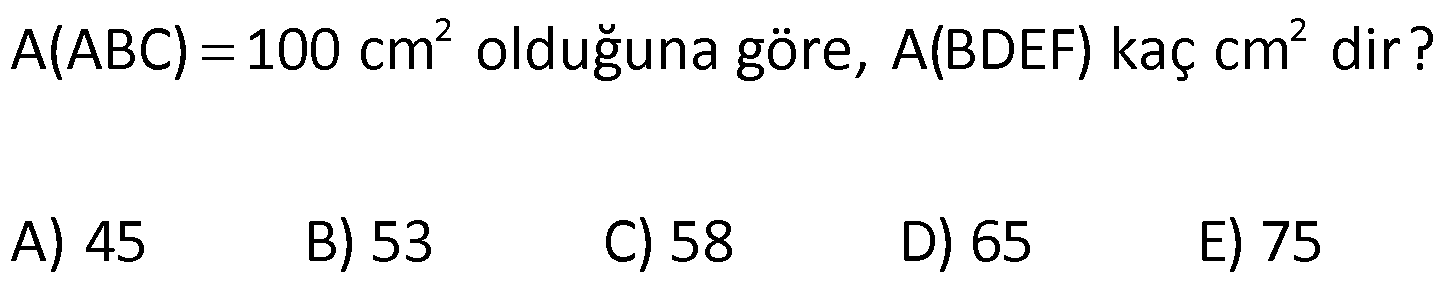

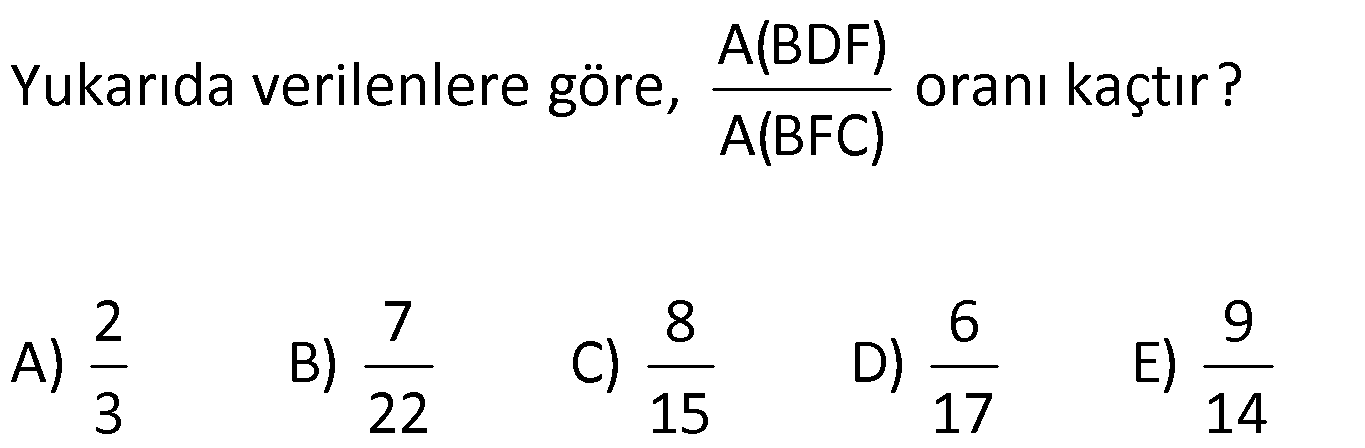



Çok güzel olmuş devamını bekleriz:)
Beğendim Güzel uygulama devamı ve geliştirilmesini bekliyorum.