 Bu bölümde Pisagor Teoremi ile ilgili 10 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…
Bu bölümde Pisagor Teoremi ile ilgili 10 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…
Eğer sorular ya da çözümler konusunda bir problem görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.
Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)
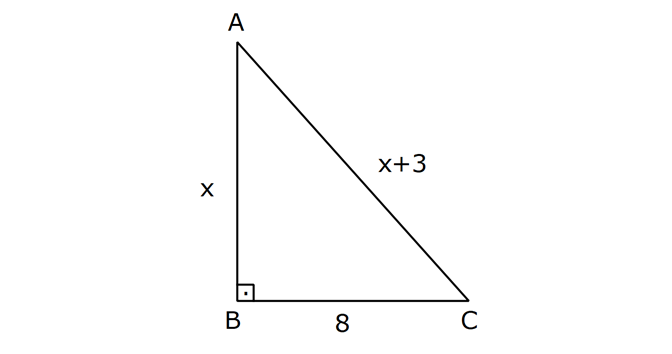
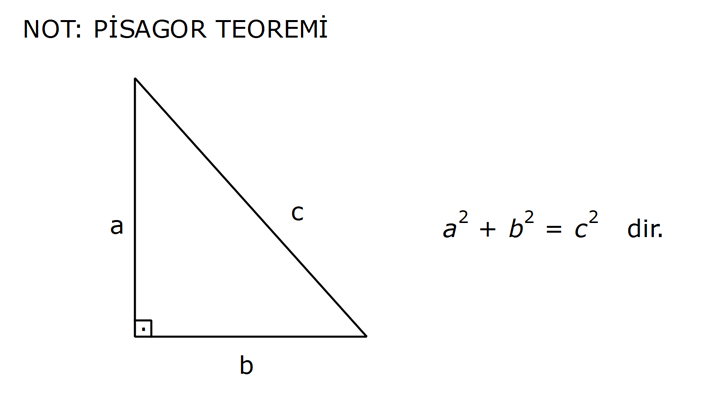
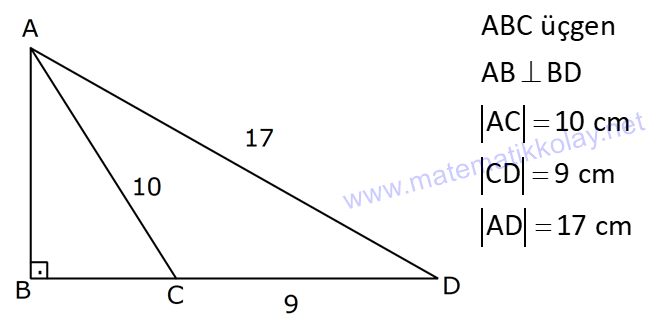
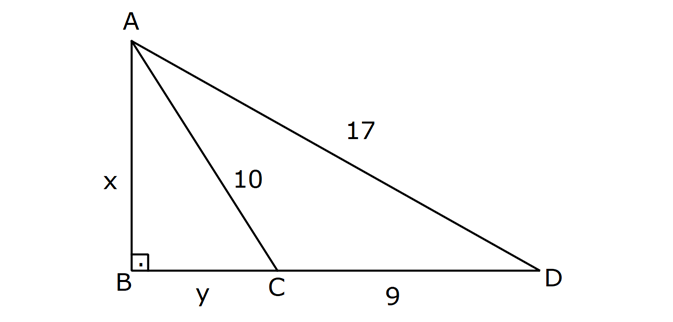
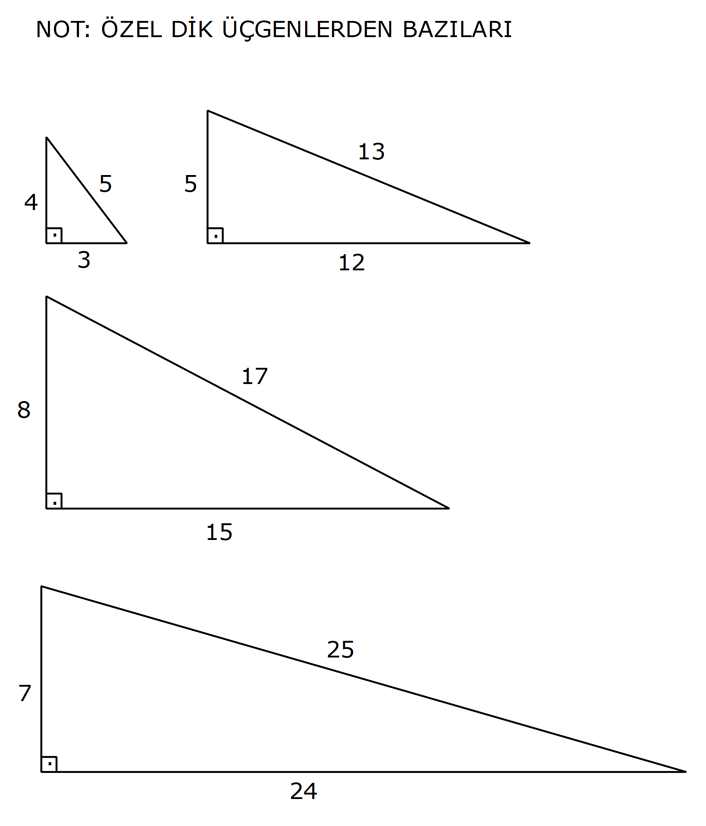
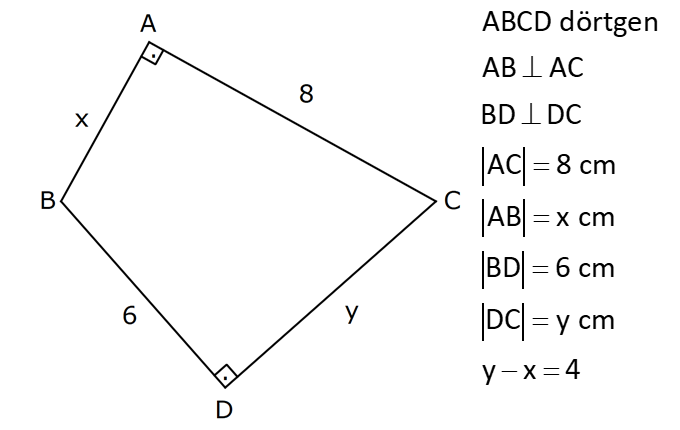
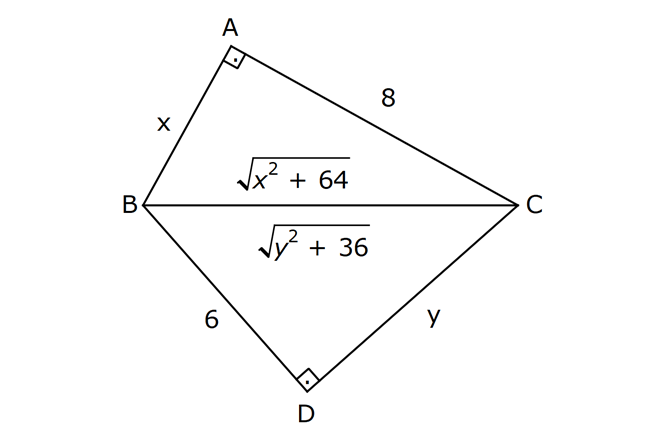
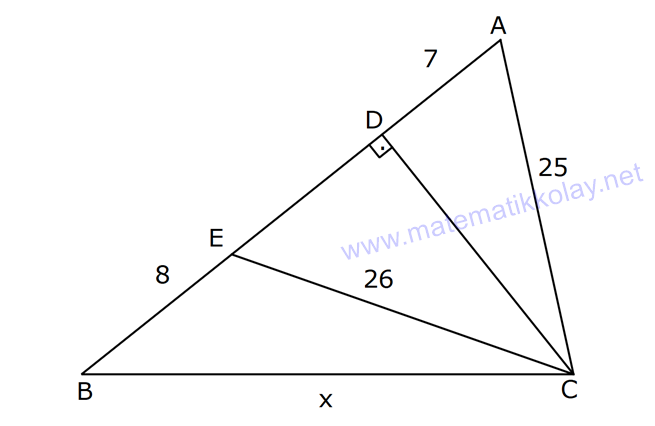
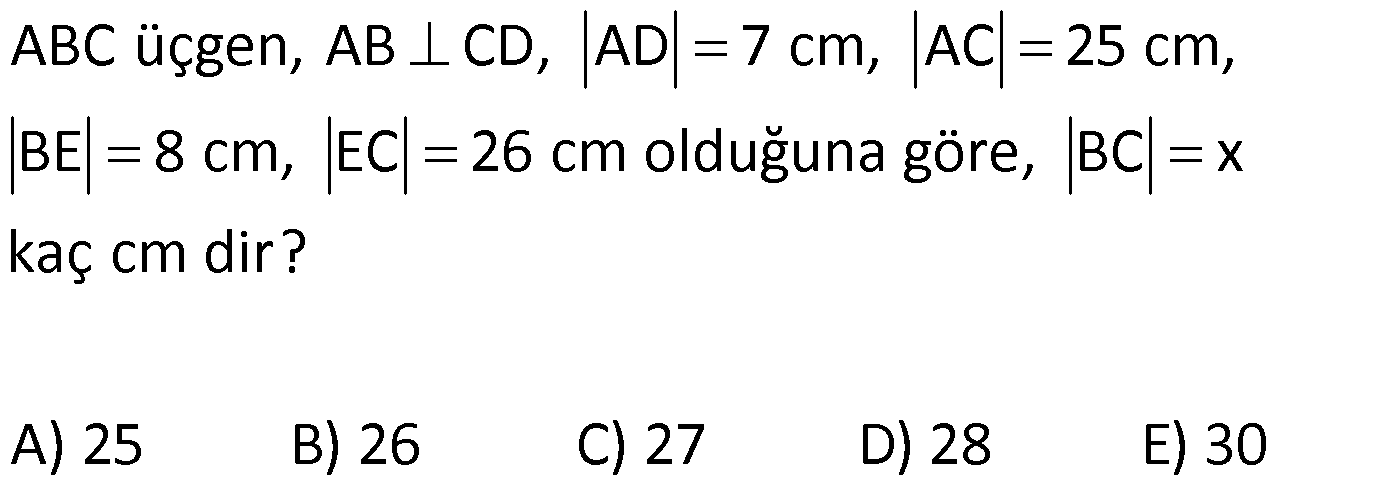
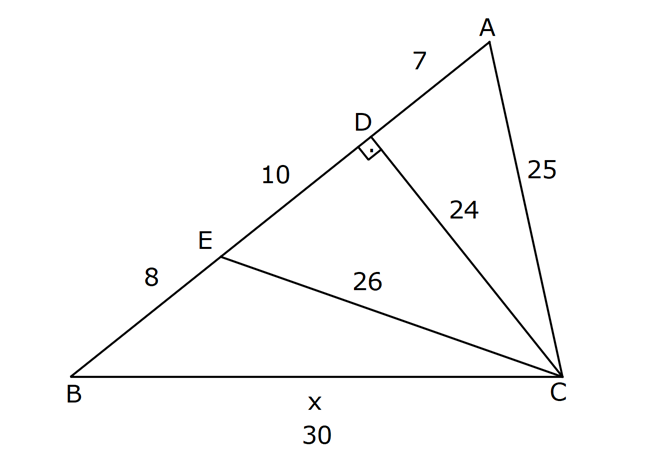
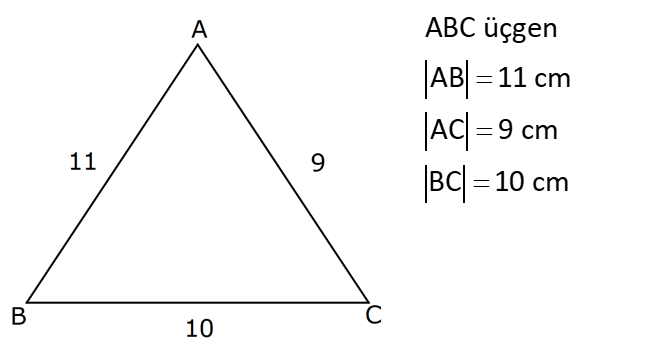
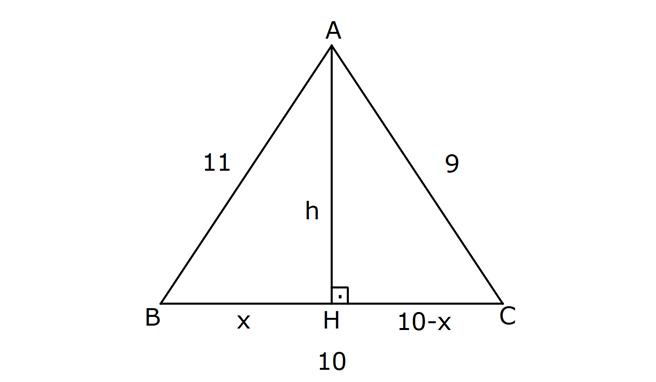
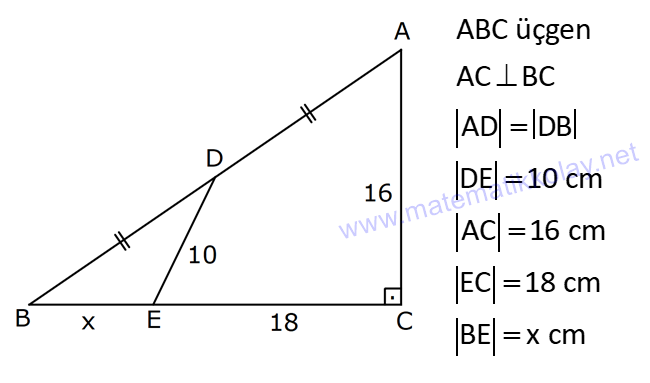
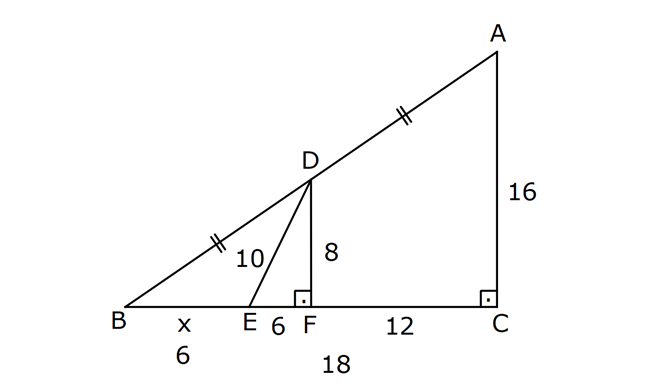
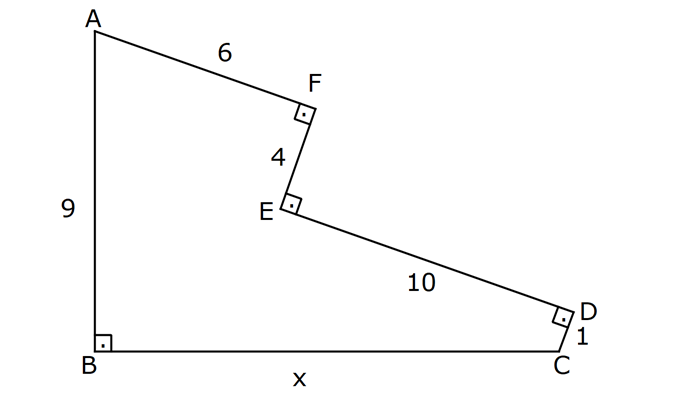
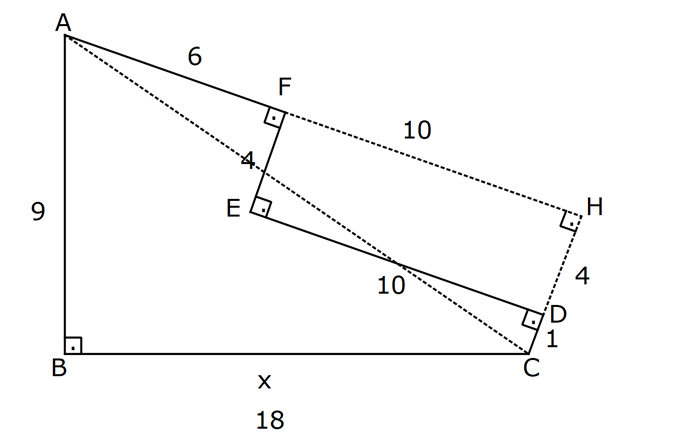
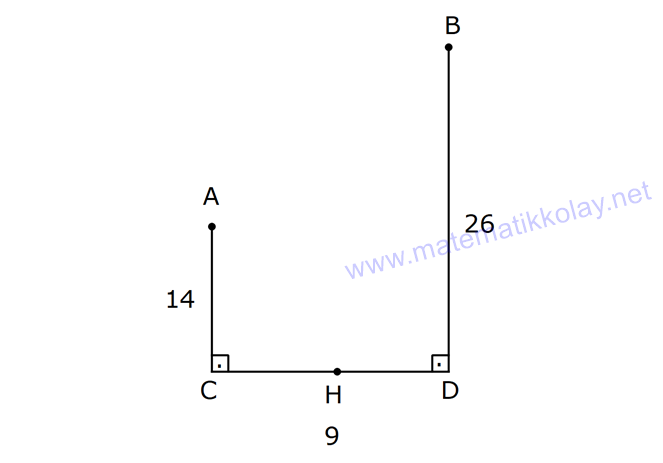
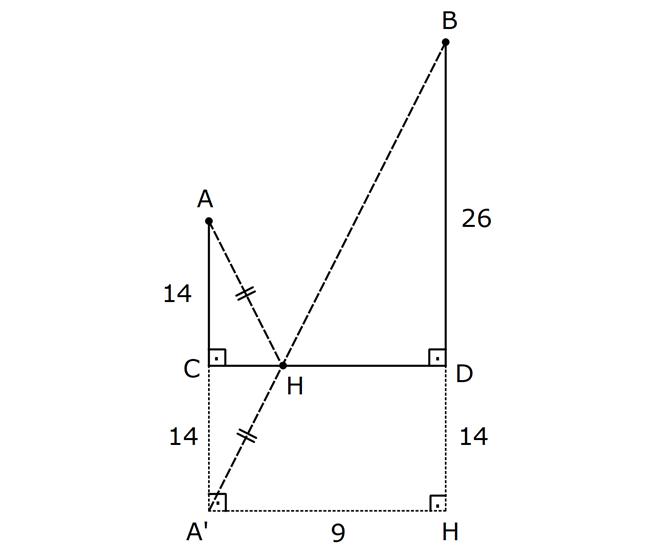
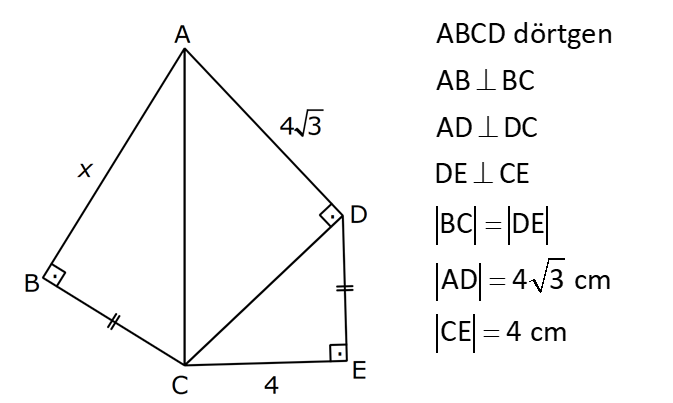
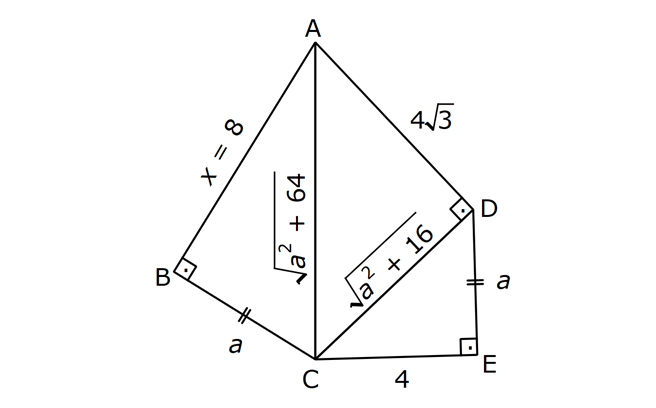
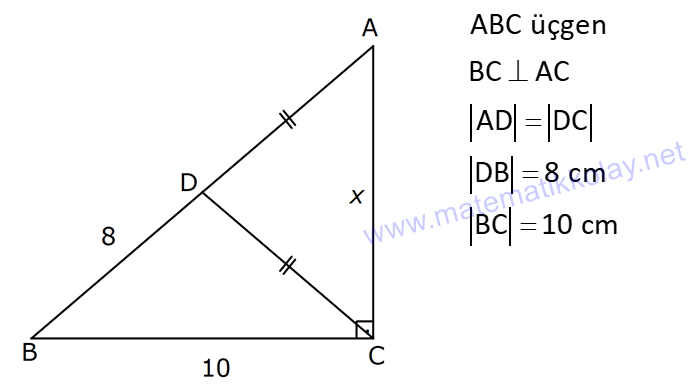
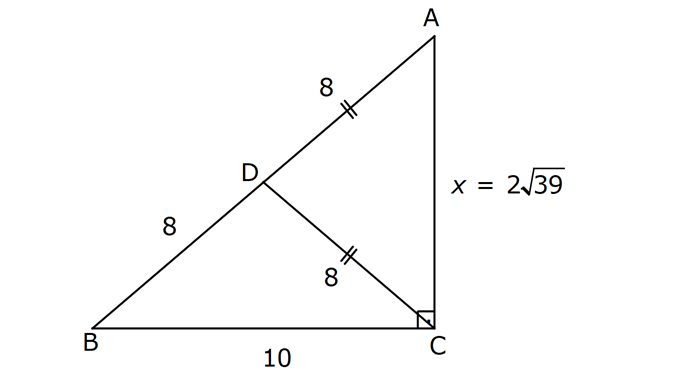
PİSAGOR www.matematikkolay.net 1) ABC üçgen BC 8 cm AC AB 3 cm AB BC Yukarıda verilenlere Ç(ABC) kaç cm dir? 55 65 76 88 A) 24 B) C) D) E) 2 3 5 3 ÇÖZÜM: 2 2 2 2 AB x olsun. AC x 3 cm olur. ABC üçgeninde pisagor teoremini uygularsak, x 8 (x 3) x 2 64 x 6x 9 64 9 6x 55 6x 55 x tir. 6 Ç(ABC) x 8 (x 3) 2x 11 2 55 6 3 11 55 88 11 tür. Cevap: E 3 3 2) ABC üçgen AB BD AC 10 cm CD 9 cm AD 17 cm Yukarıda verilenlere göre, AB kaç cm dir? A) 6 B) 8 C) 9 D) 10 E) 11 ÇÖZÜM: www.matematikkolay.net 2 2 2 2 2 2 2 100 2 2 2 2 2 ABC üçgeninde pisagor yaparsak, x y 100 dür. ABD üçgeninde pisagor yaparsak, x (y 9) 17 x y 18y 81 289 181 18y 289 18y 108 y 6 dır. ABC üçgenine geri dönelim. x 6 10 x 36 100 x 64 AB BD AD x 8 cm dir. Cevap: B Hipotenüsü 17 br olan bir özel dik üçgen var. 8 15 17 Bunu test edel II. Yol: (Özel Üçgenleri Tahmin Ederek) im. y 15 9 6 cm olur. ABC üçgeni de 6 8 10 üçgenini sağlamış oldu. (3 4 5 özel dik üçgeninin 2’şer katı) O halde AB 8 cm dir. Cevap: B 3) ABCD dörtgen AB AC BD DC AC 8 cm AB x cm BD 6 cm DC y cm y x 4 Yukarıda verilenlere göre, AB kaç cm dir? 1 3 5 11 A) B) 1 C) D) E) 2 2 2 2 ÇÖZÜM: 2 2 2 2 2 2 2 2 4 7 dir. ABC üçgeninde pisagora göre, BC x 64 tür. BDC üçgeninde pisagora göre, BC y 36 dır. İkisini birbirine eşitleyelim. x 64 y 36 28 y x 28 (y x)(y x) y x 4 y x 7 taraf taraf 11 2 a toplayalım. 11 2y 11 y dir. 2 11 3 y x 4 4 x x tir. Cevap: C 2 2 www.matematikkolay.net 4) ABC üçgen, AB CD, AD 7 cm, AC 25 cm, BE 8 cm, EC 26 cm olduğuna göre, BC x kaç cm dir? A) 25 B) 26 C) 27 D) 28 E) 30 ÇÖZÜM: ADC üçgeni bir 7 -24 -25 üçgenidir. DC 24 cm EDC üçgeni 5-12 -13 üçgeninin 2’şer katıdır. 10 -24 -26 üçgeni AD 10 cm dir. BD 10 8 18 cm olur. BDC üçgeni 3- 4 – 5 üçgeninin 6 şar katıdır. 18 -24 – 30 üçgeni x 30 cm buluruz. Cevap : E 5) ABC üçgen AB 11 cm AC 9 cm BC 10 cm Yukarıda verilenlere göre, [BC] kenarına ait yükseklik kaç cm dir? A) 6 B) 6 2 C) 6 3 D) 8 E) 8 2 ÇÖZÜM: 2 2 2 2 2 2 2 2 121 2 A köşesinden yükseklik indirelim. ABH üçgeninde pisagor yaparsak, x h 121 dir. ACH üçgeninde pisagor yaparsak, h (10 x) 81 dir. h 100 20x x 81 h x 100 20x 81 221 20x 81 140 20x x 7 cm dir. x 2 2 2 2 2 h 121 idi. 7 h 121 h 121 49 h 72 h 6 2 cm dir. Cevap : B www.matematikkolay.net 6) ABC üçgen AC BC AD DB DE 10 cm AC 16 cm EC 18 cm BE x cm Yukarıda verilenlere göre, x kaç cm dir? A) 6 B) 7 C) 8 D) 9 E) 10 ÇÖZÜM: D noktasından BC’ye dikme indirelim. 16 AD DB olduğundan DF 8 cm olur. 2 DEF üçgeni bir 6 – 8 -10 üçgenidir. EF 6 cm olur. FC 18 6 12 cm kalır. AD DB olduğundan, F noktası BC’nin orta noktasıdır. BF 12 cm d ir. x 12 6 6 cm olur. Cevap: A 7) B, D, E ve F açıları 90 olmak üzere, AB 9 cm, AF 6 cm, EF 4 cm, ED 10 cm ve DC 1 cm olduğuna göre, BC x kaç cm dir? A) 12 B) 8 2 C) 9 3 D) 10 2 E) 16 ÇÖZÜM: 2 2 2 2 2 2 Yukarıdaki gibi F ve D noktalarından, şekli uzatırsak H noktasında dik açı olur. AHC üçgeninde pisagor yaparsak, AC 16 5 256 25 281 dir. ABC üçgeninde pisagor yaparsak, 9 x 281 x 200 x 10 2 cm dir. C evap: D www.matematikkolay.net 8) AC 14 br, BD 26 br, CD 9 br, AC CD ve BD CD dir. H noktası [CD] üzerinde bir nokta olduğuna göre, AH BH toplamının en küçük değeri kaç br dir? A) 12 B) 26 C) 40 D) 41 E) 49 ÇÖZÜM: A noktasının CD doğrusuna göre simetriğini alalım. AH HB nin en az olması için H noktası A’ ile B arasında olmalıdır. Yani A’ ile B arası doğrusal olmalıdır. A’B uzunluğunu da pisagor yaparak hesaplayabil 2 2 2 2 2 iriz. A’B 9 40 A’B 81 1600 A’B 1681 A’B 41 br dir. 9 40 41 üçgeni Cevap : D 9) ABCD dörtgen AB BC AD DC DE CE BC DE AD 4 3 cm CE 4 cm Yukarıda verilenlere göre, AB x kaç cm dir? A) 8 B) 8 2 C) 10 D) 12 E) 12 2 ÇÖZÜM: 2 2 2 2 2 2 2 2 2 2 BC DE a diyelim. DEC üçgeninde pisagor yapalım. CD a 16 dır. ADC üçgeninde pisagor yapalım. AC 4 3 CD 48 a 16 a 64 tür. ABC üçgeninde de pisagor yaparsak, a 64 a x x 8 cm dir . Cevap: A www.matematikkolay.net 10) ABC üçgen BC AC AD DC DB 8 cm BC 10 cm Yukarıda verilenlere göre, AC x kaç cm dir? A) 12 B) 3 6 C) 8 2 D) 4 17 E) 2 39 ÇÖZÜM: Dik açıdan inen kenarortay, muhteşem üçlüyü oluş – turur. Bu soruda da dik açı var ve AD DC verilmiş. Dolayısıyla BD uzunluğu da bunlara eşit olacaktır. (İstenirse açıları harflendirerek BDC üçgeninin ikizk 2 2 2 2 2 enar üçgen olduğu bulunabilir.) Dolayısıyla AB 8 8 16 cm dir. ABC üçgeninde pisagor yaparak, 16 10 x 256 100 x x 156 x 156 4.39 2 39 cm dir. Cevap : E
 Bu bölümde Pisagor Teoremi ile ilgili 10 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…
Bu bölümde Pisagor Teoremi ile ilgili 10 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar… 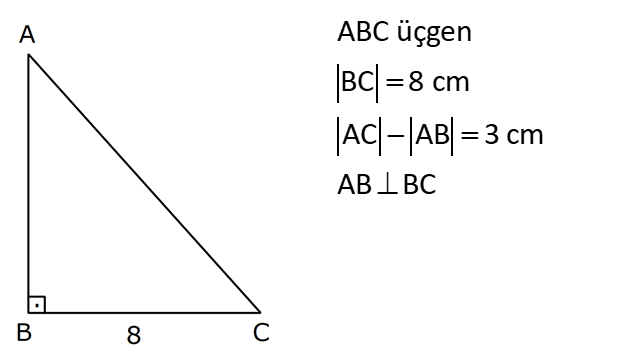
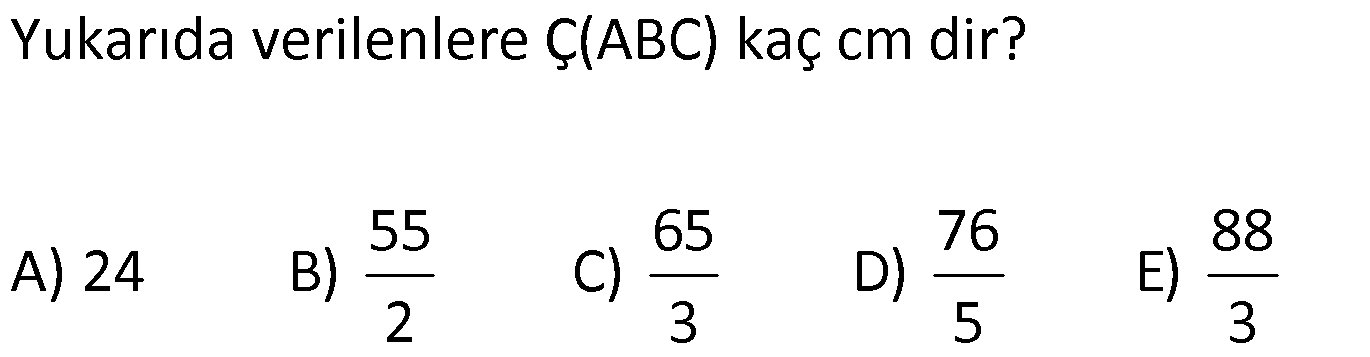

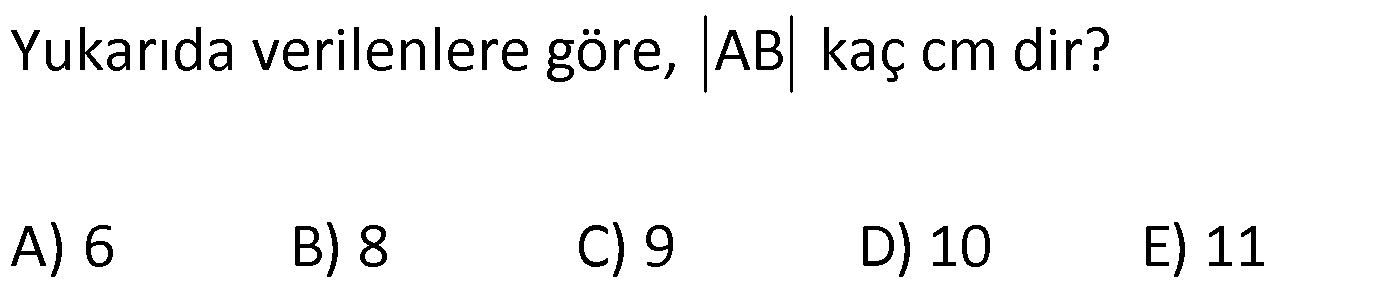

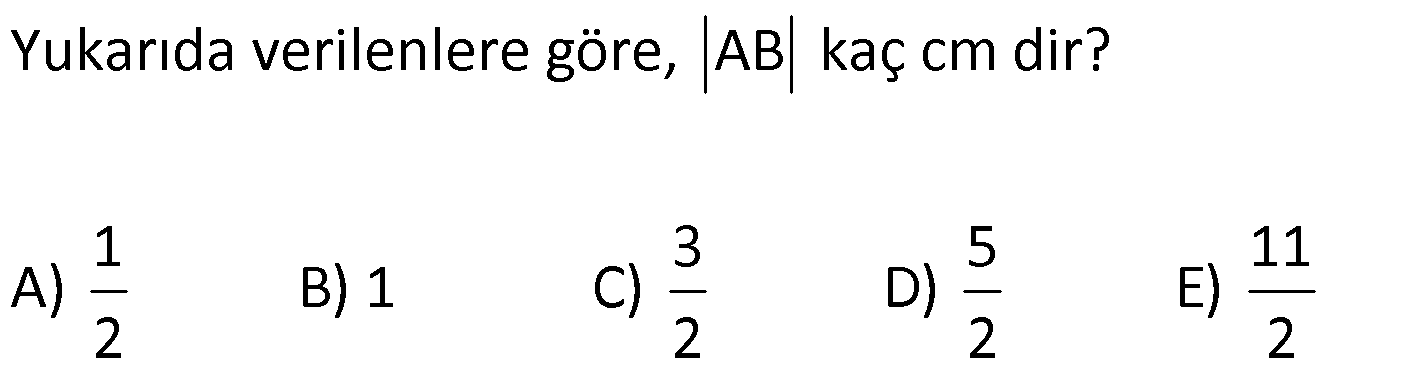


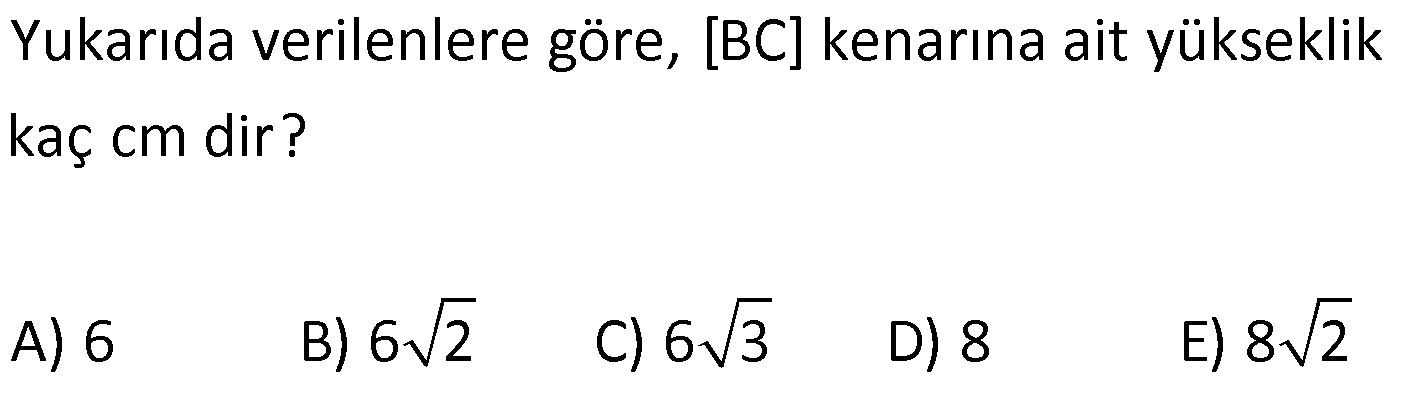

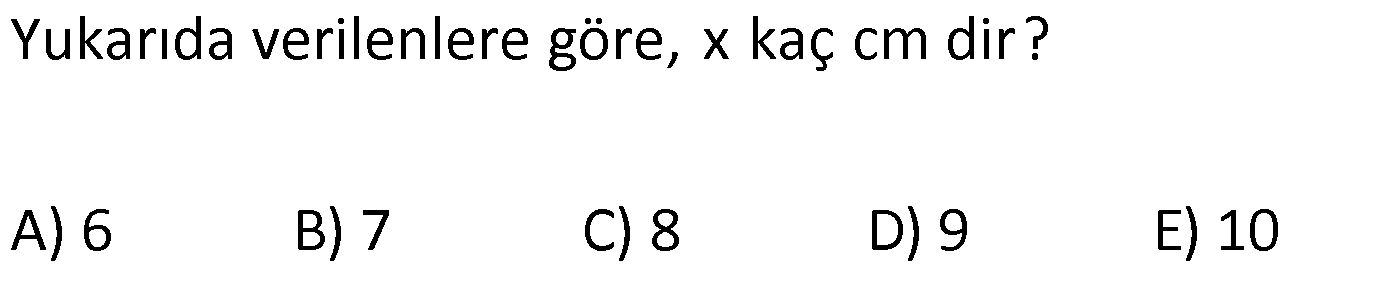






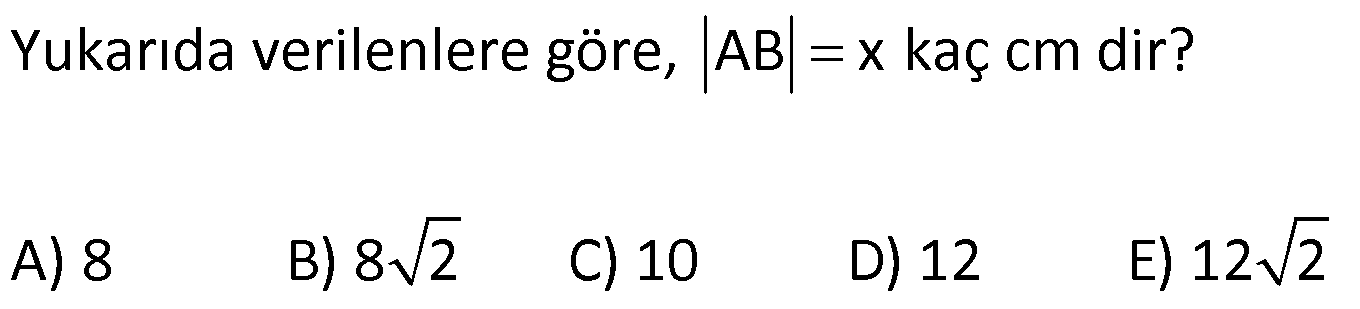


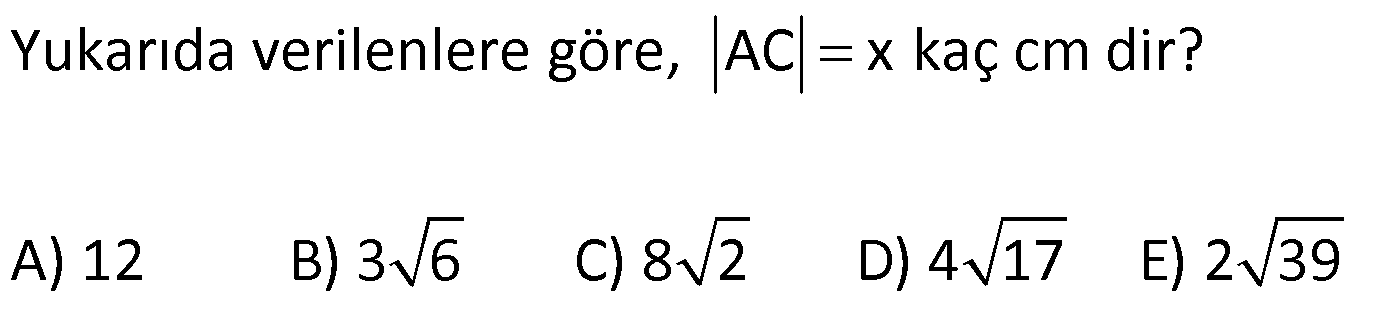



<3
Cok guzellll