Soru Sor sayfası kullanılarak Doğrunun Analitik İncelenmesi konusu altında Doğrular arasındaki alan, Eksenler arasında kalan alan ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU


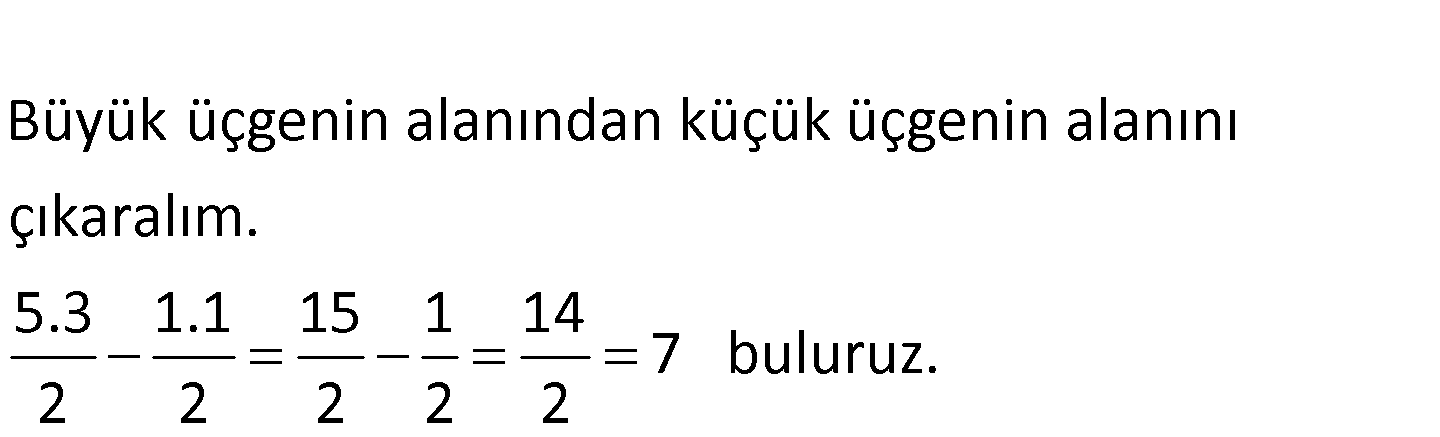
2.SORU
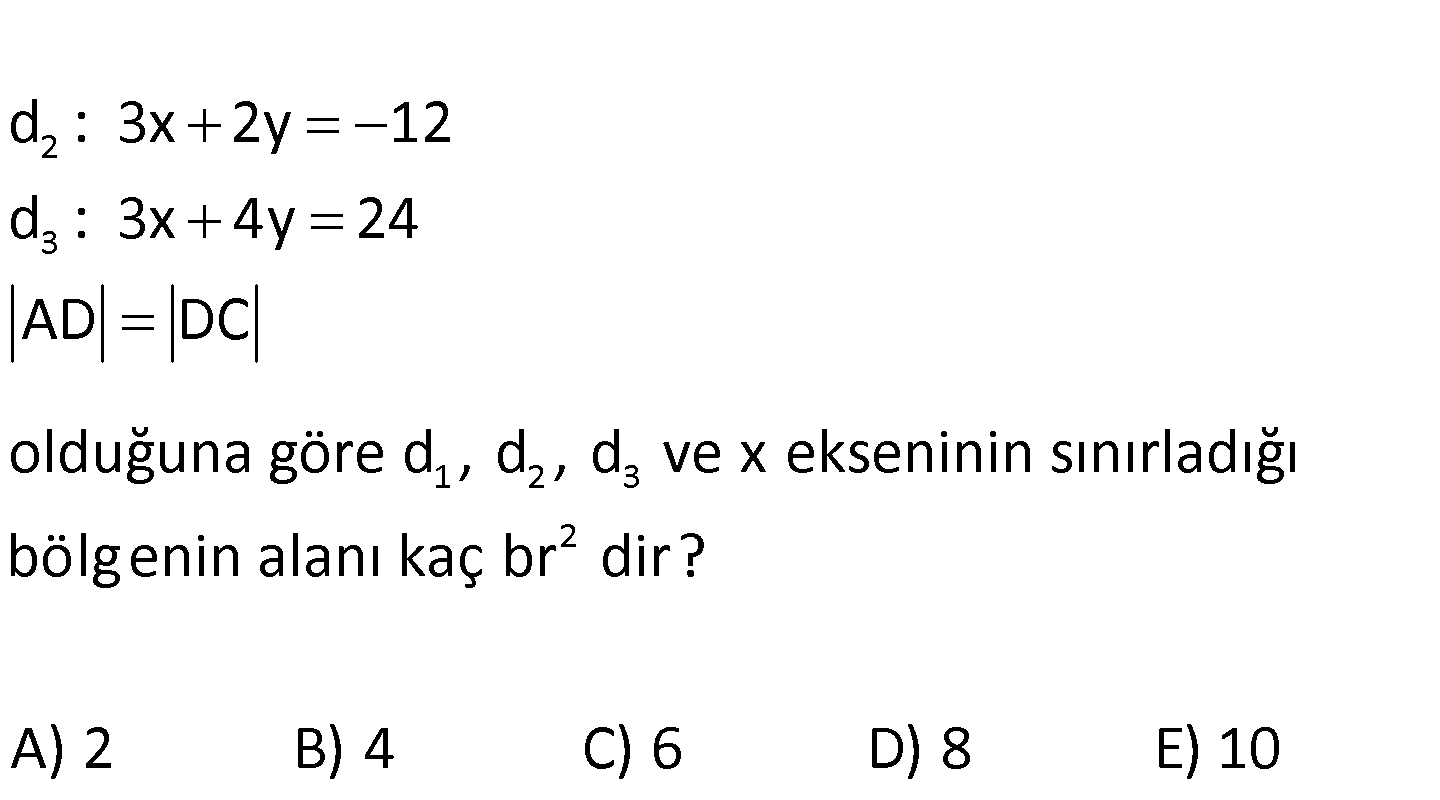

3.SORU


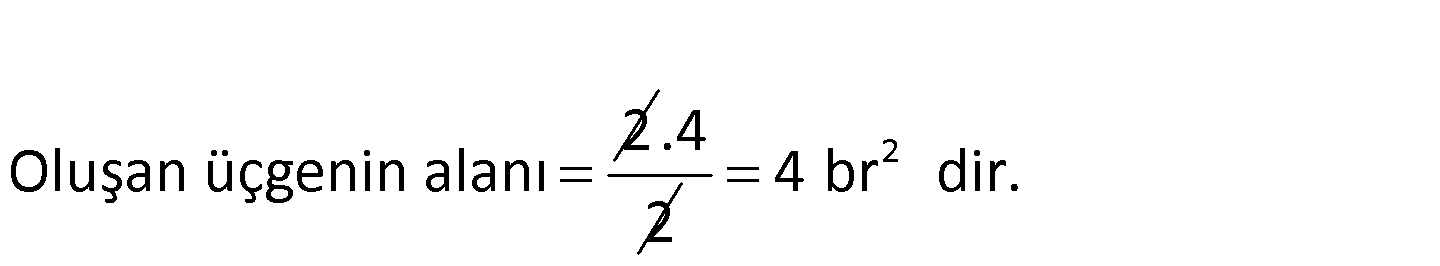
4.SORU



5.SORU


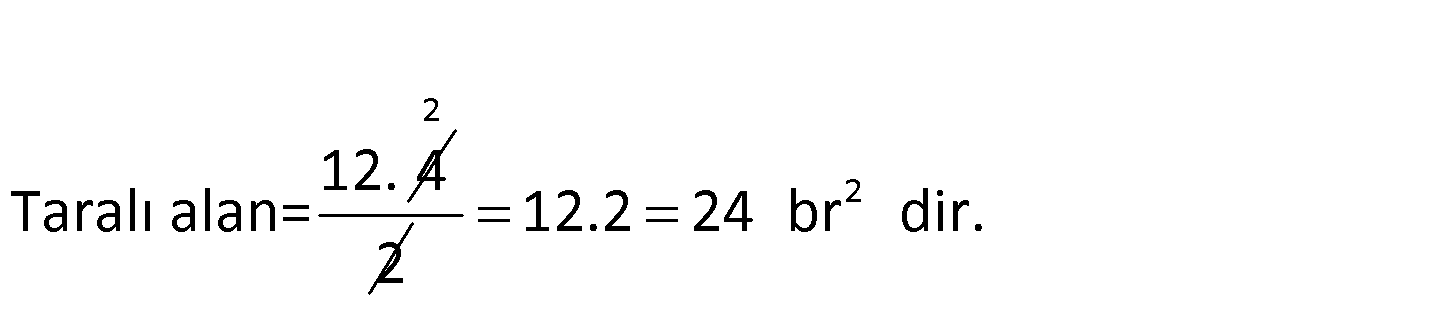
6.SORU
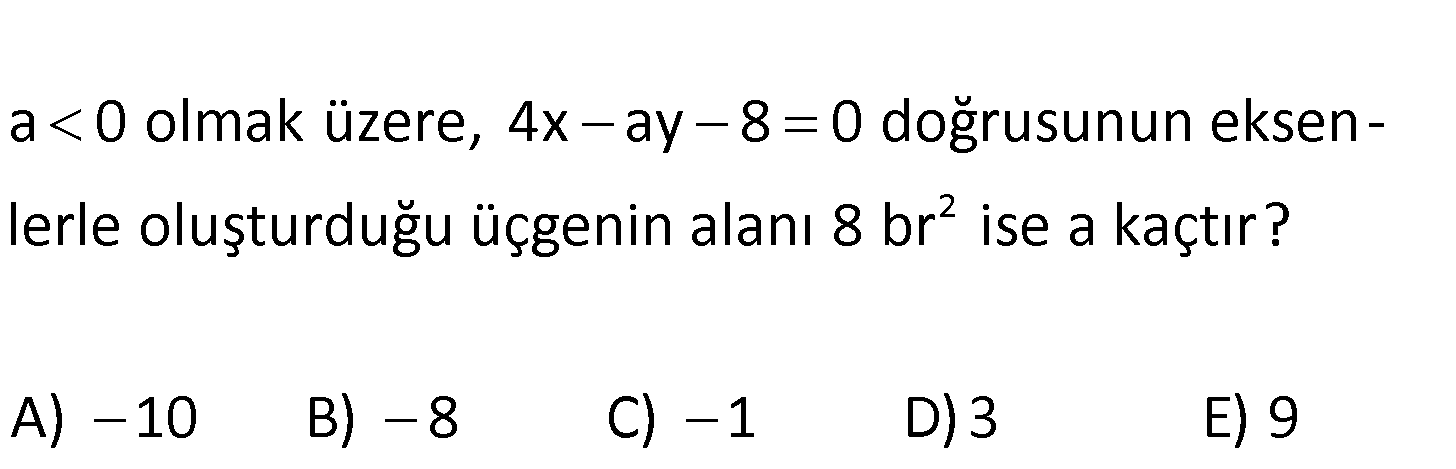

7.SORU



Diğer Soru Tipleri için Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
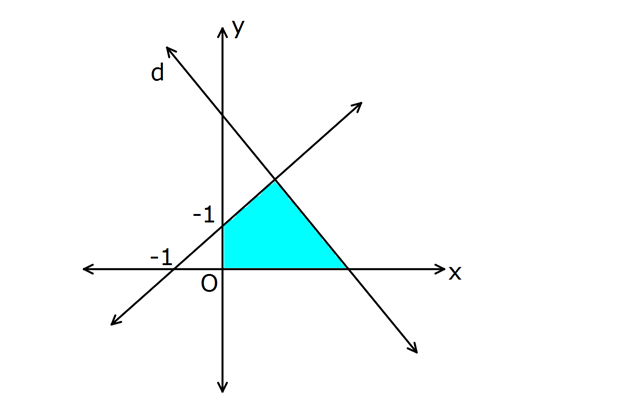
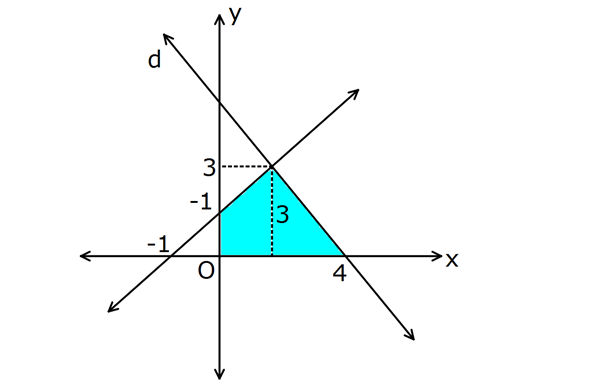
www.matematikkolay.net 2 Şekildeki d doğrusunun denklemi 3x 2y 12 0 ise taralı bölg enin alanı kaç br dir? A) 3 B) 5 C) 7 D) 9 E )11 0 d doğrusunun x eksenini kestiği nokta: 3x 2y 12 0 3x 12 0 x 4 tür. Diğer doğrunun denklemi: x y 1 1 1 ÇÖZÜM: x y 1 dir. Bu iki doğrunun kesiştiği noktada y’yi bulalım. 3x 2y 12 3 / x y 1 3x 2y 12 3x 3y 3 5y=15 y=3 tür. www.matematikkolay.net Büyük üçgenin alanından küçük üçgenin alanını çıkaralım. 5.3 1.1 15 1 14 7 buluruz. 2 2 2 2 2 34
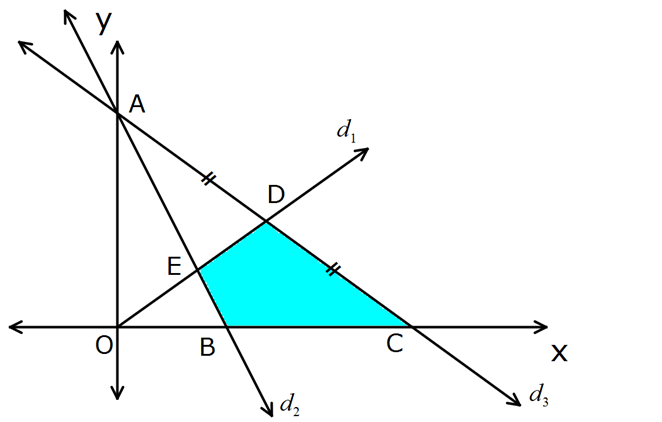
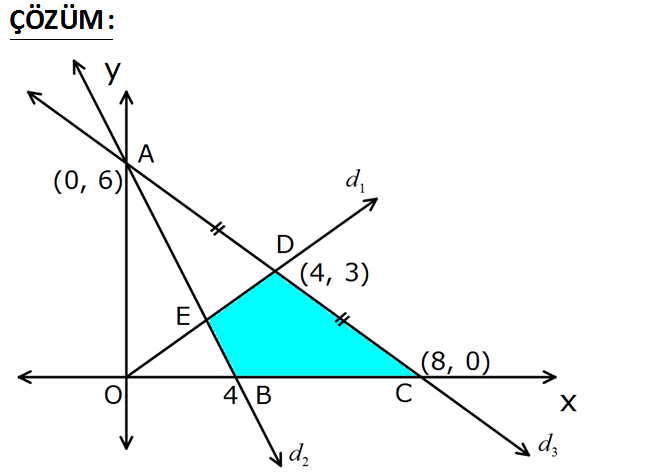
2 3 1 2 3 d : 3x 2y 12 d : 3x 4y 24 AD DC olduğuna göre d , d , d ve x ekseninin sınırladığı bölgenin alanı kaç 2 br dir? A) 2 B) 4 C) 6 D) 8 E) 10 ÇÖZÜM: www.matematikkolay.net 3 d doğrularının eksenleri kestiği noktaları bulalım. 0,6 ve 8,0 D noktası bu iki nok tanın orta noktas 1 1 2 2 ı olduğundan; 0 8 6 0 4 , 3 2 2 D 4,3 bulunur. d doğrusu eksenleri 0,0 ve 4,3 noktalarında kesiyor. d doğrusunun denklemini yazalım. y 0 x 0 3 0 4 0 y x 4y 3x 0 dır. 3 4 d ve d doğrularının kesim nokt ası olan E noktasını bulalım. Alan için ordinatını bulmak yeterli. 3x 2y 12 4y 3x 2 0 6y 12 y 2 dir. A BCDE A ODC A OEB 3.8 2.4 A BCDE 12 4 8 br bulunur. 2 2 48
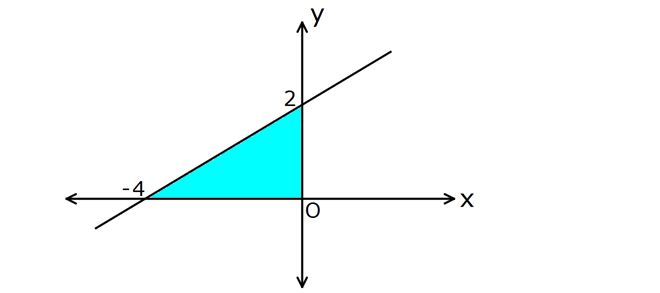
3y 2x k 1 0 doğrusu orjinden geçmektedir. Buna göre, (k 3)y kx 4 0 doğrusu ile eksenler arasında kala 2 n bölgenin alanı kaç br dir? A) 4 B) 6 C) 8 D) 10 E)12 0 0 Orjinden geçiyorsa, 0, 0 noktası bu doğru denk – lemini sağlamalıdır. 3y 2x k 1 0 k 1 0 k 1 dir. O ÇÖZÜM: 0 0 halde; k 3 y kx 4 0 1 3 y 1 x 4 0 2y x 4 0 doğrusunu elde ederiz. Eksenleri kesen noktaları bulalım. x 0 için 2y x 4 0 y 2 dir. y 0 için 2y x 4 0 x 4 tür. www.matematikkolay.net 2 Oluşan üçgenin alanı .4 2 2 4 br dir. 58
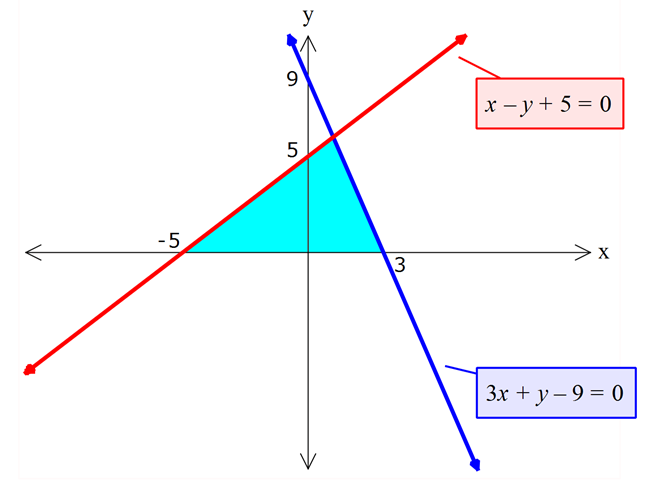
www.matematikkolay.net 2 3x y 9 0 x y 5 0 doğruları ve x ekseniyle sınırlı bölg enin alanı kaç br dir? A) 18 B) 20 C) 24 D) 26 E) 30 Ekseni kesen noktaları bulalım. 3x y 9 0 x 0 için y 9 dur. y 0 için x 3 tür. x y 5 0 x 0 için y 5 ti ÇÖZÜM: r. y 0 için x 5 tir. Buna göre, çizim yapalım. www.matematikkolay.net Birbirini kestikleri noktaya ihtiyacımız var. Çözüm kümesini bulalım. 3x y 9 0 x y 5 0 1 taraf tarafa toplayalım. 4x 4 0 x 1 dir. 3x y 9 0 3 y 9 0 y 6 dır. 1,6 noktasında kesişiyorlar. O halde oluşan üçgenin yüksekliği 6 birimdir. Tabanı ise 3 5 8 birimdir. Alan 08.Haz 3 2 24 buluruz. 62
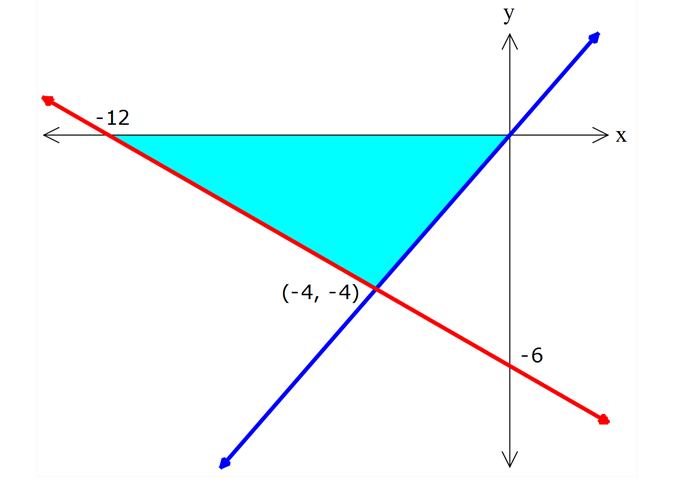
www.matematikkolay.net 2 Birinci açıortay doğrusu, 2y x 12 0 doğrusu ve x ekseninin sınırladığı bölg enin alanı kaç br dir? A) 24 B) 30 C) 36 D) 42 E) 60 0 Eksenleri kestiği noktaları bulalım. x 0 için 2y x 12 0 2y 12 ÇÖZÜM: 0 x y 6 dır. y 0 için 2y x 12 0 x 12 dir. 1.açıortay doğrusu y x doğrusudur. y x ile 2y x 12 0 doğrularının kesiştiği yeri bulalım. y x ise 2y x 12 0 2x x 12 3x 12 x 4 tür. O halde kesiştikleri yer ( 4, 4) noktasıdır. Bunu çizerek görelim. www.matematikkolay.net 12.Nis Taralı alan= 2 2 2 12.2 24 br dir. 68
2 a 0 olmak üzere, 4x ay 8 0 doğrusunun eksen – lerle oluşturduğu üçgenin alanı 8 br ise a kaçtır? A) 10 B) 8 C) 1 D) 3 E) 9 www.matematikkolay.net 0 Eksenleri kestiği noktaları bulalım. x 0 için 4x ay 8 0 ay 8 0 ÇÖZÜM: 0 ay 8 8 y dır. a y 0 için 4x ay 8 0 4x 8 x 2 dir. 8 Eksenleri kestiği noktalar 2 ve dır. a Burada oluşan üçgenin alanı 2 8 br ise; 8 2 a 8 eşitliğini kurabiliriz. 2 2 8 a 2 8 a 1 a 1 dir. a 0 69
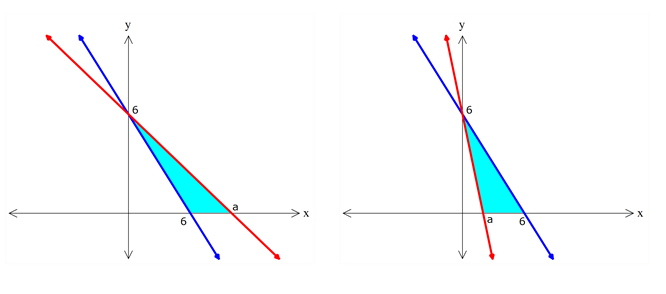
2 x y x y 6 doğrusu, 1 doğrusu ve x ekseni ile a 6 sınırlı üçgensel bölg enin alanı 12 br olduğuna göre, a nın alabileceği değerler toplamı laçır? A) 12 B) 14 C) 15 D)16 E) 18 www.matematikkolay.net 0 0 0 Eksenleri kestiği noktaları bulalım. x 0 için x y 6 y 6 y 0 için x y 6 x 6 dır. x y x 0 için a ÇÖZÜM: 0 1 y 6 6 x y y 0 için 1 x a dır. a 6 a’nın durumuna göre 2 farklı alan oluşur. Bunlar; a 6 .6 İlk şekle göre; 12 a 6 . 6 2 24 4 a 10 olmalıdır. 6 a .6 2. şekle göre; 12 6 a . 6 2 24 4 a 2 olmalıdır. O halde; a’nın değerleri toplamını 2 10 12 buluruz. www.matematikkolay.net 70

