Bir bileşik önerme, bileşenlerinin bütün doğruluk değerleri için doğru (1) oluyorsa totoloji, yanlış (0) oluyorsa çelişki olarak tanımlanır.
Örnek 1 için Tıklayınız.
![]() ve
ve ![]() önermelerinin doğruluk değerlerini tablo yaparak inceleyiniz.
önermelerinin doğruluk değerlerini tablo yaparak inceleyiniz.
Çözüm için Tıklayınız.
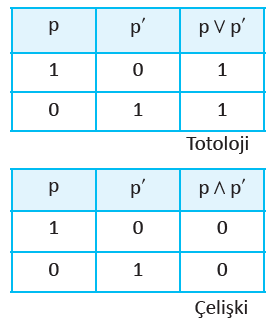
![]() bileşik önermesi, p nin tüm doğruluk değerleri için doğru (1) olduğundan bir totolojidir.
bileşik önermesi, p nin tüm doğruluk değerleri için doğru (1) olduğundan bir totolojidir.
![]() bileşik önermesi, p nin tüm doğruluk değerleri için yanlış (0) olduğundan bir çelişkidir.
bileşik önermesi, p nin tüm doğruluk değerleri için yanlış (0) olduğundan bir çelişkidir.
Örnek 2 (Totoloji)
![]() bileşik önermesinin totoloji olduğunu gösteriniz.
bileşik önermesinin totoloji olduğunu gösteriniz.
Çözüm için Tıklayınız.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() (Totoloji)
(Totoloji)
Örnek 3 (Çelişki)
![]() bileşik önermesinin çelişki olduğunu gösteriniz.
bileşik önermesinin çelişki olduğunu gösteriniz.
Çözüm için Tıklayınız.
![]()
![]()
![]()
![]()
![]()
![]()
Örnek 4 (Totoloji)
![]() bileşik önermesinin totoloji olduğunu gösteriniz.
bileşik önermesinin totoloji olduğunu gösteriniz.
Çözüm için Tıklayınız.
![]()
![]()
![]()
![]()
![]()
![]()
ve / veya Bağlaçlarının Elektrik Devrelerinde Kullanılışı
Sembolik mantığın matematik dışında elektrik devrelerinde de kullanım alanı vardır. Elektrik devrelerinde akımın geçmesi 1, geçmemesi 0 ile gösterilirse tüm elektrik devreleri sembolik mantık ile ifade edilebilir.
Açık anahtar (akım geçirmeyen anahtar):  şeklinde gösterilir. p anahtarı açık ise doğruluk değeri
şeklinde gösterilir. p anahtarı açık ise doğruluk değeri ![]() olur.
olur.
Kapalı anahtar (akım geçiren anahtar):  şeklinde gösterilir. p anahtarı kapalı ise doğruluk değeri
şeklinde gösterilir. p anahtarı kapalı ise doğruluk değeri ![]() olur.
olur.
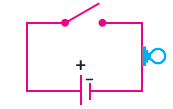
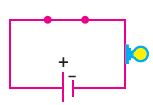
Elektrik devrelerinde seri bağlama  şeklinde çizilir.
şeklinde çizilir. ![]() ile gösterilir.
ile gösterilir.
Elektrik devrelerinde paralel bağlama 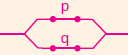 şeklinde çizilir.
şeklinde çizilir. ![]() ile gösterilir.
ile gösterilir.
Örnek 5 (Lamba yanar mı?)
Aşağıdaki şekilde verilen elektrik devresine karşı gelen bileşik önermeyi yazınız. Bu önermeye göre lambanın yanıp yanmayacağını belirtiniz.
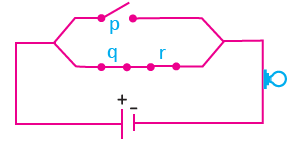
Çözüm için Tıklayınız.
Şekilde q ve r anahtarları seri, p anahtarı ise bu anahtarlara paralel bağlanmıştır. Bu durumda elektrik devresine karşı gelen bileşik önerme ![]() olur.
olur.
p anahtarı açık olduğundan akım geçirmez. ![]() olur.
olur.
q ve r anahtarları kapalı olduğundan akım geçirir. ![]() ve
ve ![]() olur.
olur.
Bulunan doğruluk değerleri bileşik önermede yerine yazılırsa
![]()
![]()
![]()
![]() bulunur. Bu durumda devreden akım geçer ve lamba yanar
bulunur. Bu durumda devreden akım geçer ve lamba yanar
Örnek 6 (Elektrik Devresini Çiz.)
![]() olduğuna göre,
olduğuna göre,
![]() bileşik önermesine karşı gelen elektrik devresini çiziniz.
bileşik önermesine karşı gelen elektrik devresini çiziniz.
Çözüm için Tıklayınız.
p, q, s anahtarları kapalı; r, t anahtarları açık konumdadır.
r ile t seri bağlı ve bunlar q ile paralel bağlıdır.
p ile s seri bağlı ve bunlar yukarıdakilerin tamamıyla paralel bağlıdır. Buna göre, aşağıdaki devreyi çizebiliriz.
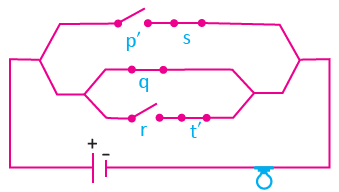
Lamba yanar mı?
Çözüm için Tıklayınız.
![]() değerlerini yazarsak,
değerlerini yazarsak,
![]()
![]()
![]()
![]()
![]()
![]() dir. Lamba yanar.
dir. Lamba yanar.

