Soru Sor sayfası kullanılarak Trigonometri-2 konusu altında Yarım Açı formüllerinden yararlanarak denklem çözme, Toplam fark formüllerinden yararlanarak denklem çözme ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
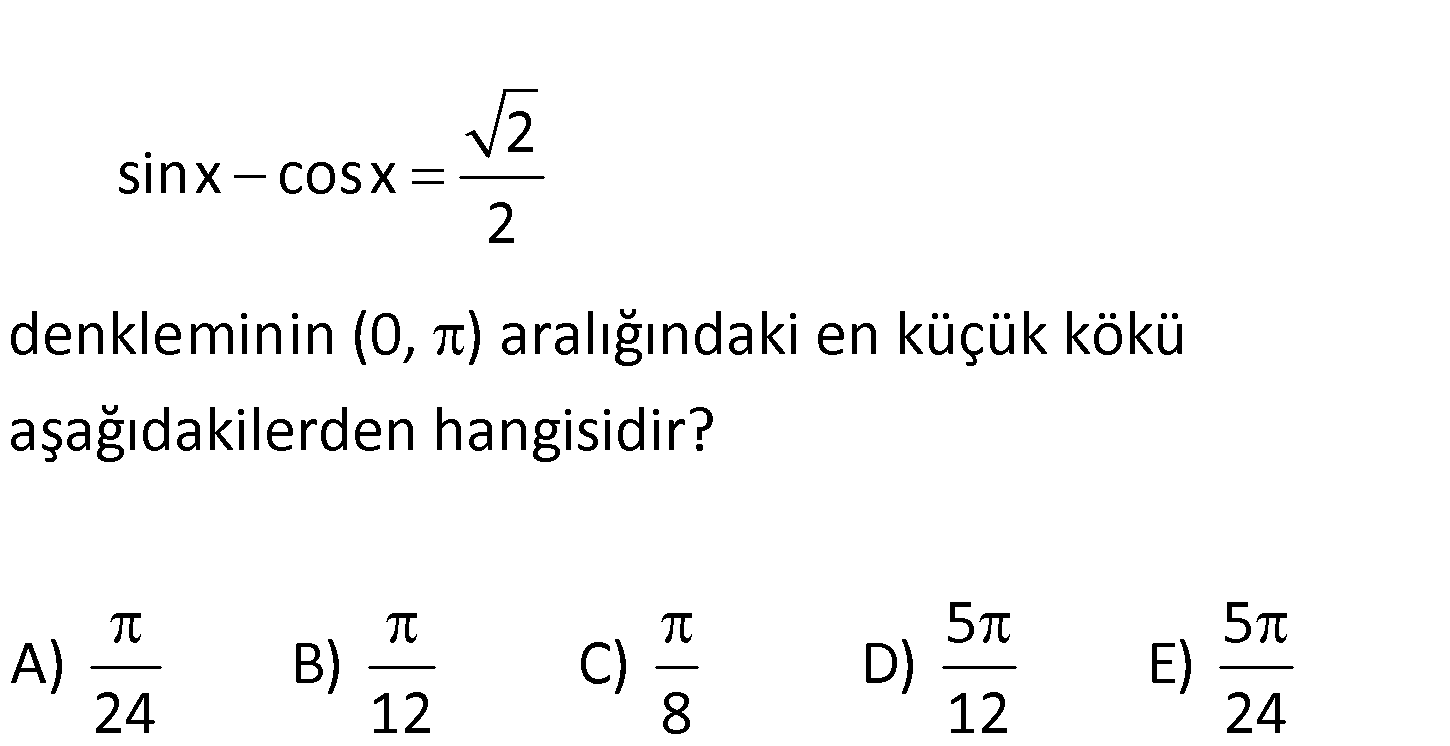

2.SORU

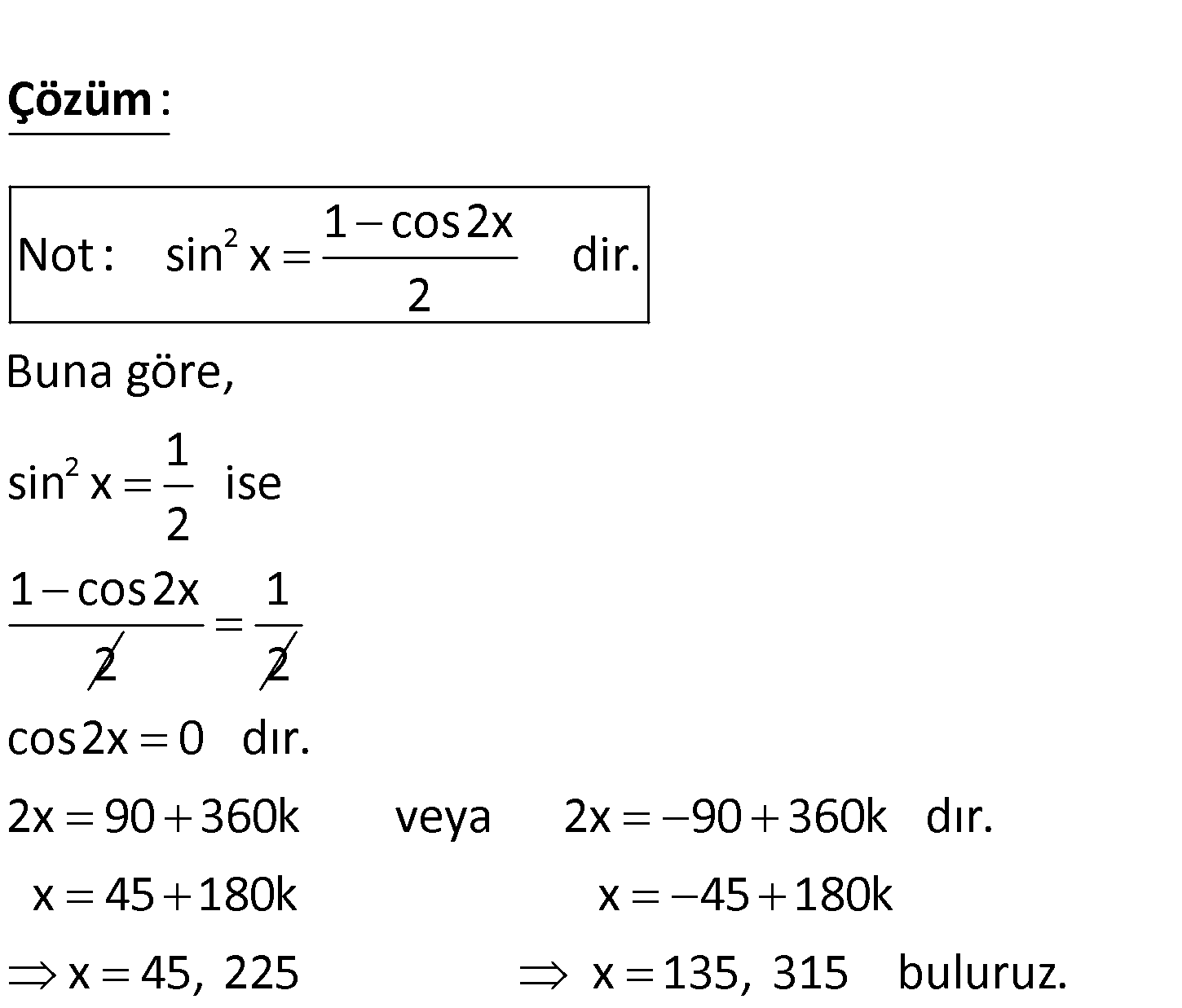
3.SORU
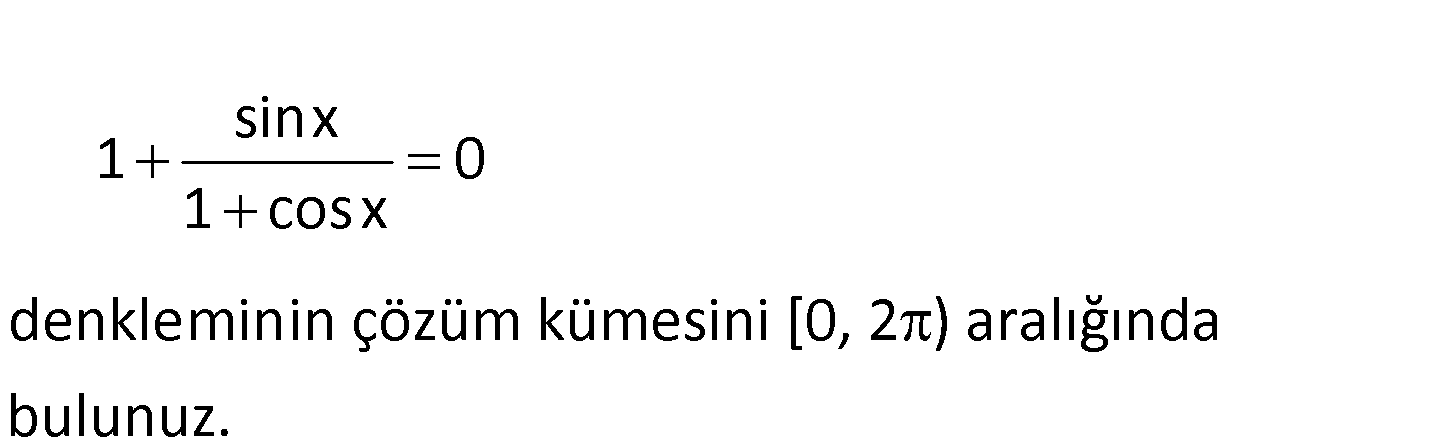
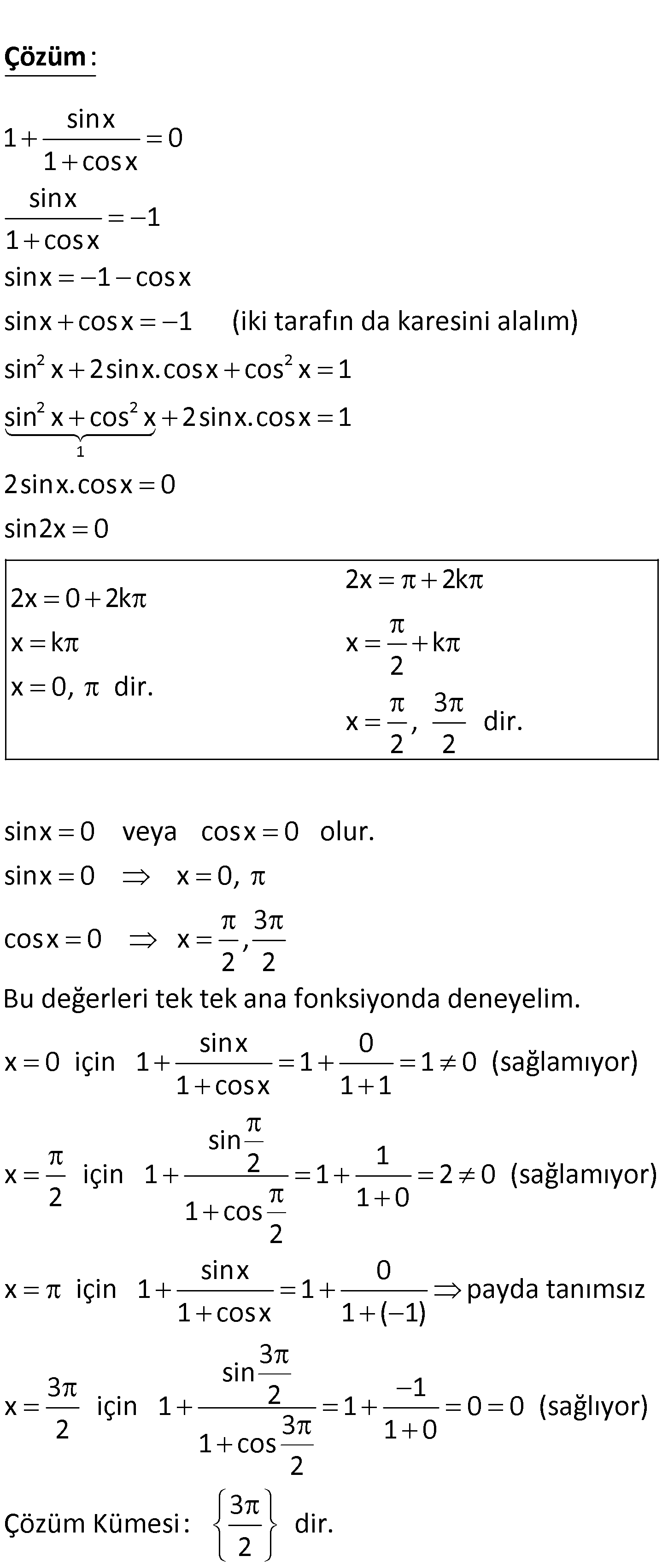
4.SORU

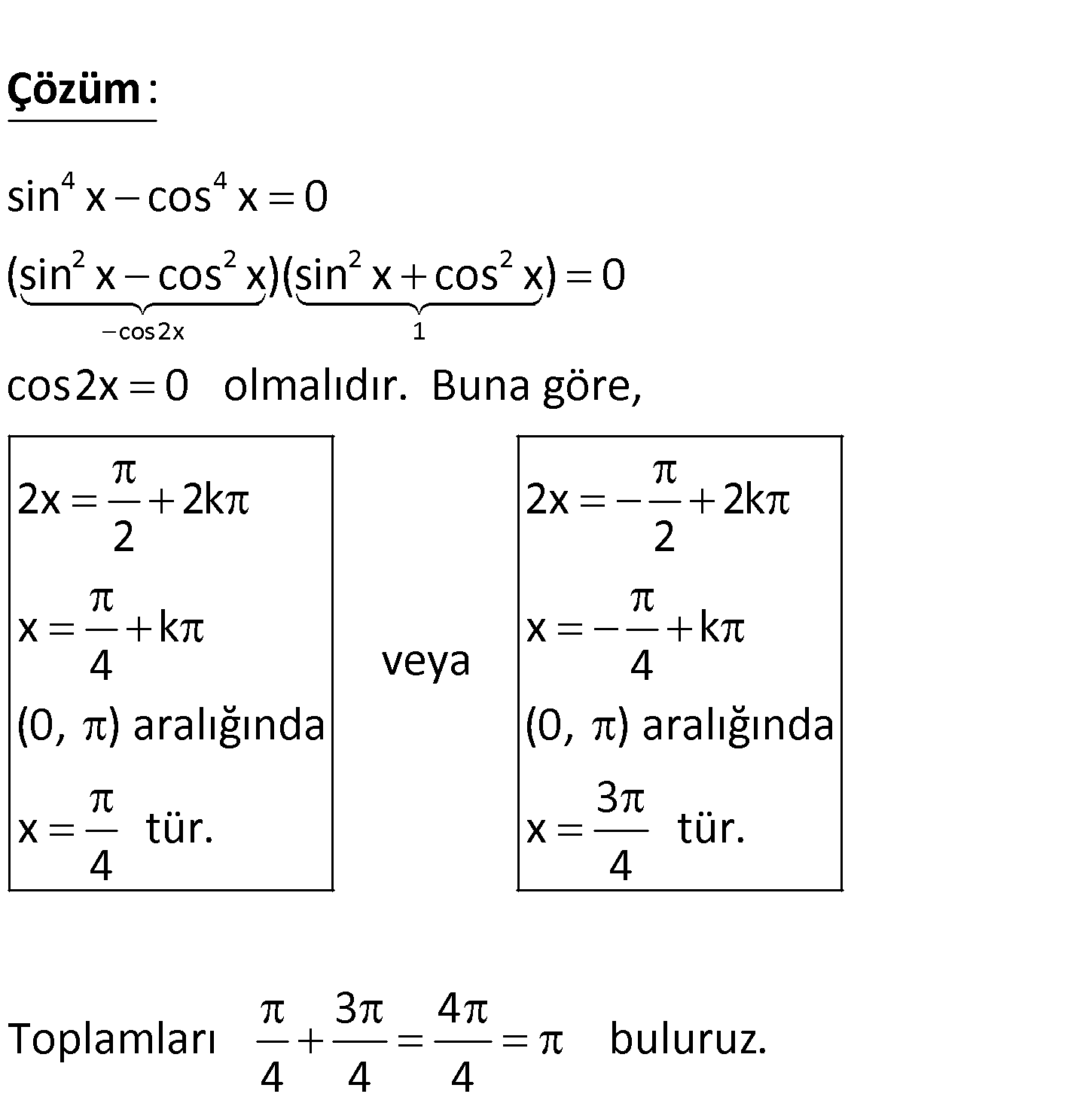
5.SORU

6.SORU
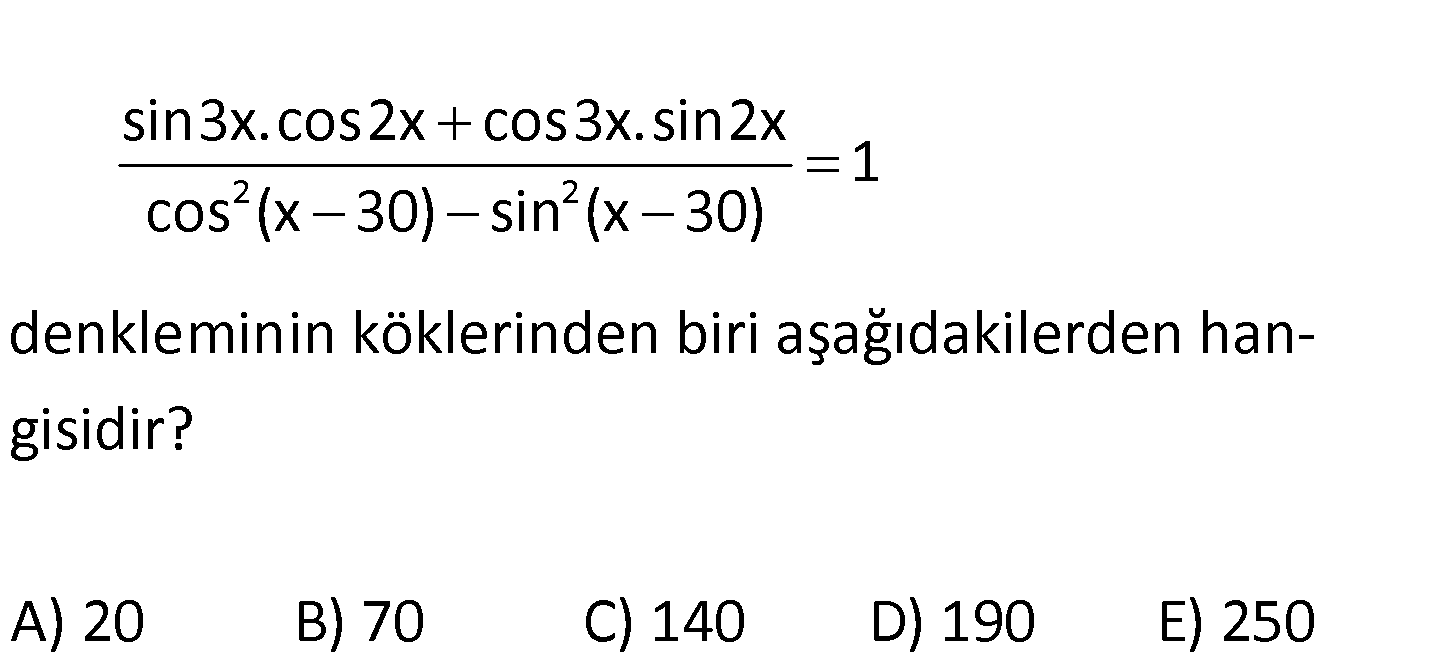

7.SORU


8.SORU


Diğer Soru Tipleri için Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
2 sinx cosx 2 denkleminin (0, ) aralığındaki en küçük kökü aşağıdakilerden hangisidir? A) B 24 5 5 ) C) D) E) 12 8 12 24 www.matematikkolay.net 2 2 1 2 sinx cosx Kare alalım. 2 2 sin x cos x 2sinx.cosx 4 1 1 2sinx.cosx 2 1 : 1 sin2x 2 Çözüm 1 sin2x 2 1 sin2x 2 5 2x veya dır. 6 6 5 x veya olur. 12 12 Ancak x değeri sinx cos x ifadesini pozitif 12 değil negatif yapar. Çünkü cos x değeri daha büyüktür. Bu sebeple x değerini 12 alamayız. 5 Cevap: olur. 12 43
2 1 sin x 2 denkleminin [0, 360) aralığındaki köklerini bulunuz. www.matematikkolay.net 2 2 1 cos2x Not : sin x dir. 2 Buna göre, 1 sin x ise 2 1 cos2x 2 : Çözüm 1 2 cos2x 0 dır. 2x 90 360k veya 2x 90 360k dır. x 45 180k x 45 180k x 45, 225 x 135, 315 buluruz. 44
sinx 1 0 1 cosx denkleminin çözüm kümesini [0, 2 ) aralığında bulunuz. www.matematikkolay.net sinx101cosxsinx11cosxsinx1cosxsinxcosx1 (iki tarafın da karesini alalım:)sinÇözüm22221x2sinx.cosxcosx1sinxcosx2sinx.cosx12sinx.cosx0sin2x0 2x2k2x02kxkxk2x0, dir.3x, dir. 22sinx0 veya cosx0 olur.sinx0 x0 , 3cosx0 x,22Bu değerleri tek tek ana fonksiyonda deneyelim.sinx0x0 için 1110 (sağlamıyor)1cosx11sin12x için 1120 (sağlamıyor)2101cos2sinxx için 111cosx 0payda tanımsız1(1)3sin312x için 1100 (sağlıyor)32101cos23Çözüm Kümesi: dir.2 www.matematikkolay.net 2
4 4 0 x olmak üzere, sin x cos x eşitliğini sağlayan x değerlerinin toplamı kaçtır? 3 A) B) 2 4 5 C) D) E) 2 3 4 (LYS 2013) www.matematikkolay.net 4 4 2 2 2 2 cos2x 1 sin x cos x 0 (sin x cos x)(sin x cos x) 0 cos2x 0 olmalıdır. Buna gö : r Çözüm e, 2x 2k 2x 2k 2 2 x k x k 4 veya 4 (0, ) aralığında (0, ) aralığında 3 x tür. x tür. 4 4 3 4 Toplamları buluruz. 4 4 4 13
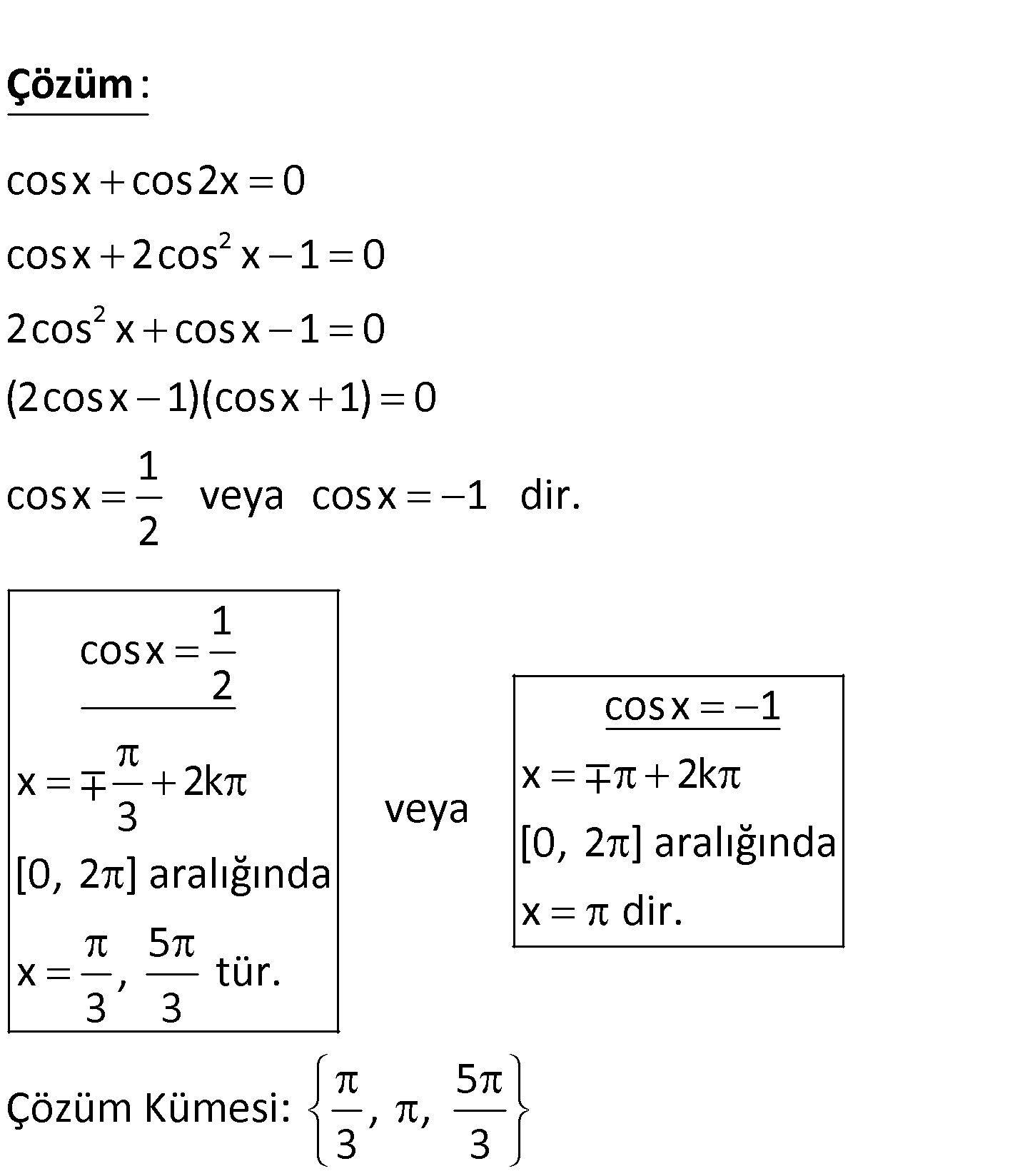
cosx cos2x 0 denkleminin [0, 2 ] aralığındaki köklerini bulunuz. www.matematikkolay.net 2 2 cosx cos2x 0 cosx 2cos x 1 0 2cos x cosx 1 0 (2cosx 1)(cosx 1) 0 1 cosx veya cosx 1 dir. 2 : Çözüm 1 cosx 2 cosx 1 x 2k x 2k 3 veya [0, 2 ] aralığında [0, 2 ] aralığında x dir. 5 x , tür. 3 3 5 Çözüm Kümesi: , , 3 3 20
2 2 sin3x.cos2x cos3x.sin2x 1 cos (x 30) sin (x 30) denkleminin köklerinden biri aşağıdakilerden hangisidir? A) 20 B) 70 C) 140 D) 190 E) 250 www.matematikkolay.net 2 2 sin3x.cos2x cos3x.sin2x 1 cos (x 30) sin (x 30) sin(3x 2x) sin(5x) 1 1 cos 2(x 30) cos 2x : 60 si Çözüm n5x cos(2x 60) sinüsü , kosinüse çevirelim. cos(90 5x) cos(2x 60) ya açılar birbirine eşit, ya da zıt işaretlidir. 90 5x 2x 60 360k 90 5x 2x 60 360k 7x 150 360k 90 5x 2x 60 360k 7x 150 360k 3x 30 360k 150 360k x 10 120k x 7 10, 130, 250, … 150 510 870 , , ,… 7 7 7 E şıkkı 250 bu denklemi sağlar. 27
www.matematikkolay.net x 0, olmak üzere, 2 1 sin2x secx 1 cos( x) sin(2 x) denkleminin kökü kaç radyandır ? A) B) C) D) E) 6 4 3 2 2 2 2 1 sin2x secx 1 cos( x) sin(2 x) sin x cos x 2sinx.cosx secx 1 cosx sinx (sinx cosx) secx (si : Çözüm 1 nx cosx) (sinx cosx) secx 1 (sinx cosx) secx 1 1 secx 2 1 cosx x buluruz. 2 3 30
2 cos x sin4x denkleminin köklerinden biri aşağıdakilerden hangisidir? 3 7 A) B) C) D) 4 3 5 3 5 E) 2 www.matematikkolay.net 2 2 2 cos x sin4x cos x 2sin2x.cos2x cos x 4sinx.cosx.cos2x Eşitliğin iki tarafında da cos x var. Eğe : r Çözüm cosx 0 olursa bu eşitliği sağlar. x k için cosx 0 dır. 2 5 E şıkkı değeri de buna uygundur. 2 5 cos cos 2 cos 0 dır. 2 2 2 Bu sebeple E şıkkı, bu denklemin köklerinden biridir . 41

