Soru Sor sayfası kullanılarak Trigonometri-1 konusu altında Trigonometride Periyot, Trigonometrik fonksiyonların periyodunu bulma, Periyodu okek yardımıyla bulma ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…

1.SORU


2.SORU


3.SORU
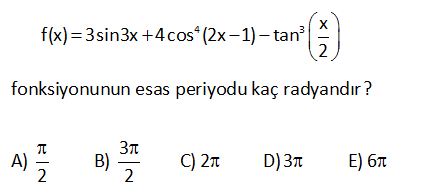

4.SORU
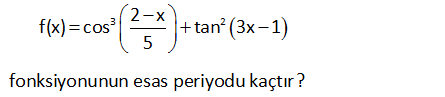

5.SORU


6.SORU
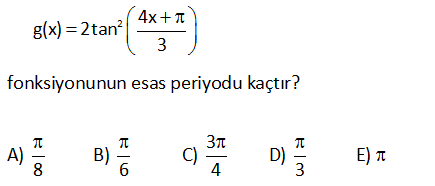

Diğer Soru Tipleri için Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
3 5cot (2x 5) cos 3x 4 fonksiyonunun esas periyodu kaçtırA) B) 2 C) 3 D) 4 E) 5 3 Fonksiyonu iki parça halinde inceleyelim. 5cot (2x 5) ‘in periyodu dir. 2 cos(3x 4) ‘ e : in p Çözüm 2 riyodu tür. 3 Bu ikisinin toplamı olan f(x) fonksiyonun esas periyo – du OKEK’leridir. Buna göre; 2 OKEK( , 2 ) 2 OKEK( , ) 2 buluruz. 2 3 OBEB(2, 3) 1 NOT: m m 2 , m tek ise f(x) a bsin (cx d) c T g(x) a bcos (cx d) , m çift ise c f ???m m (x) a btan (cx d) T dir. g(x) a bcot (cx d) c Not : sinx ve cosx ‘in periyodu 2 tanx ve cotx ‘in periyodu dir. ??43
2 f(x) 3cos4x 2sin x fonksiyonunun esas periyodunu bulunuz. 2 2 periyot periyot 4 2 1 f(x) 3cos4x 2sin x f(x)’in periyodu da bu iki periyodun O E ‘ : K K Çözüm i dir. OKEK( , ) OKEK( , ) buluruz. 2 OBEB(2,1) 1 8
4 3 x f(x) 3sin3x 4cos (2x 1) tan 2 fonksiyonunun esas periyodu kaç radyandır3 A) B) C) 2 2 2D) 3E) 6 4 3 4 x f x 3sin3x 4cos 2x 1 tan 2 2 2 sin3x a 3 çift derecede esas periyot cos 2x 1 a 2 di : Çözüm 3 r. x tan 2 dir. 2 a 1 2 üçünün ekoku esas periyottur. esas periyot 2 olur. 21
3 2 2 x f(x) cos tan 3x 1 5 fonksiyonunun esas periyodu kaçtır a 2 x cos in esas periyodunu bulalım; 5 2 1 2 2 cos x T 10 dir. 5 5 a 1 5 kosinüs : Çözüm 3 a ün tek kuvvetlerinde periyot değişmez. 2 x O halde cos ‘in periyodu 10 dir. 5 tan(3x 1) in esas periyodunu bulalım; tan(3x 1) T tür. a 3 tanjantın tüm kuvvetlerinde periyot aynıdır. O halde tan 2 3 (3x 1)’in esas periyodu tür. 3 2 x f(x) cos tan(3x 1) in esas periyodu; 5 ekok(10 , ) T ekok 10 , 10 buluruz. 3 ebob(1,3) 26
4 f(x) 2 3cos (3x) fonksiyonunun esas periyodu kaçtırA) B) C) D) E) 8 6 4 3 Fonksiyondaki kosinüsün kuvveti çift olduğundan; Periyodu 2 değil, üzerinden hesaplaya : cağ Çözüm ız. Kosinüsün içindeki x’in katsayı 3 olduğundan, 3’e böleceğiz. Periyot buluruz. 3 46
2 4x g(x) 2tan 3 fonksiyonunun esas periyodu kaçtır3 A) B) C) D) E) 8 6 4 3 Tanjant fonksiyonun periyodu üzerinden hesaplanır. 4 Tanjantın içindeki x ‘in katsayı : oldu 3 Çözüm ğundan, 3 3 Periyot buluruz. 4 4 4 3 47

