Soru Sor sayfası kullanılarak Trigonometri-1 konusu altında Şekilli trigonometri soruları ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
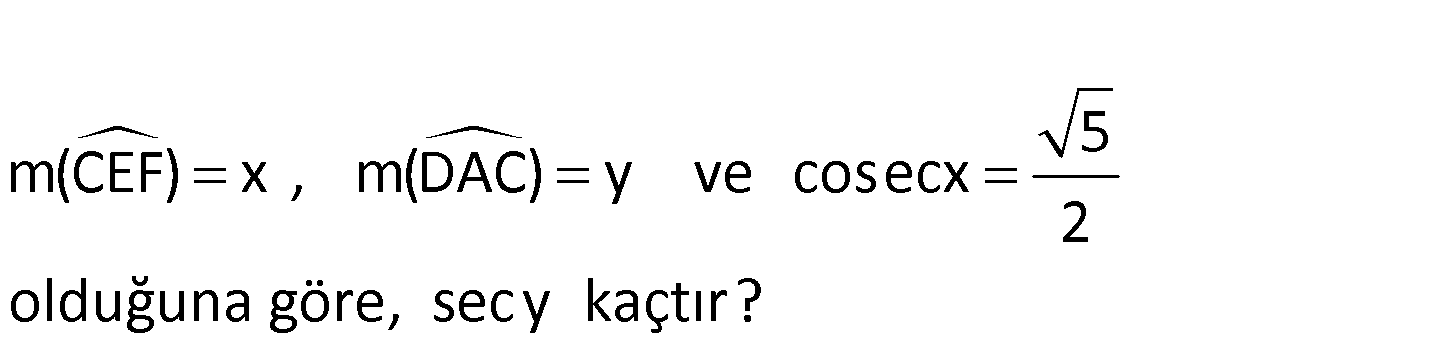

2.SORU


3.SORU
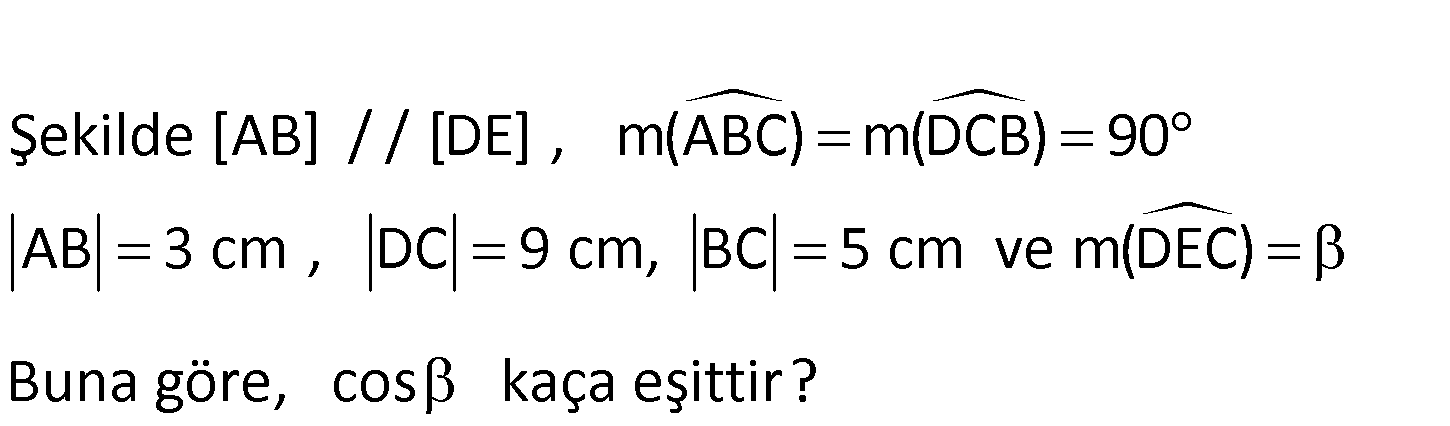

4.SORU
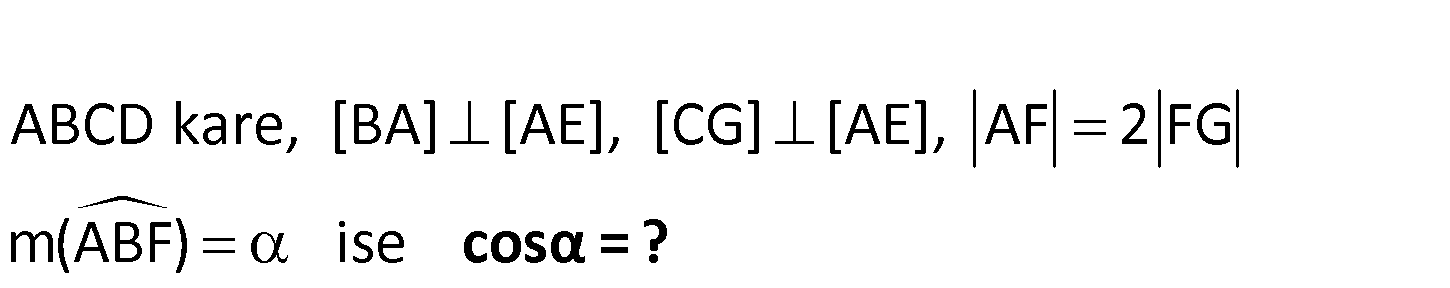

5.SORU


6.SORU

7.SORU
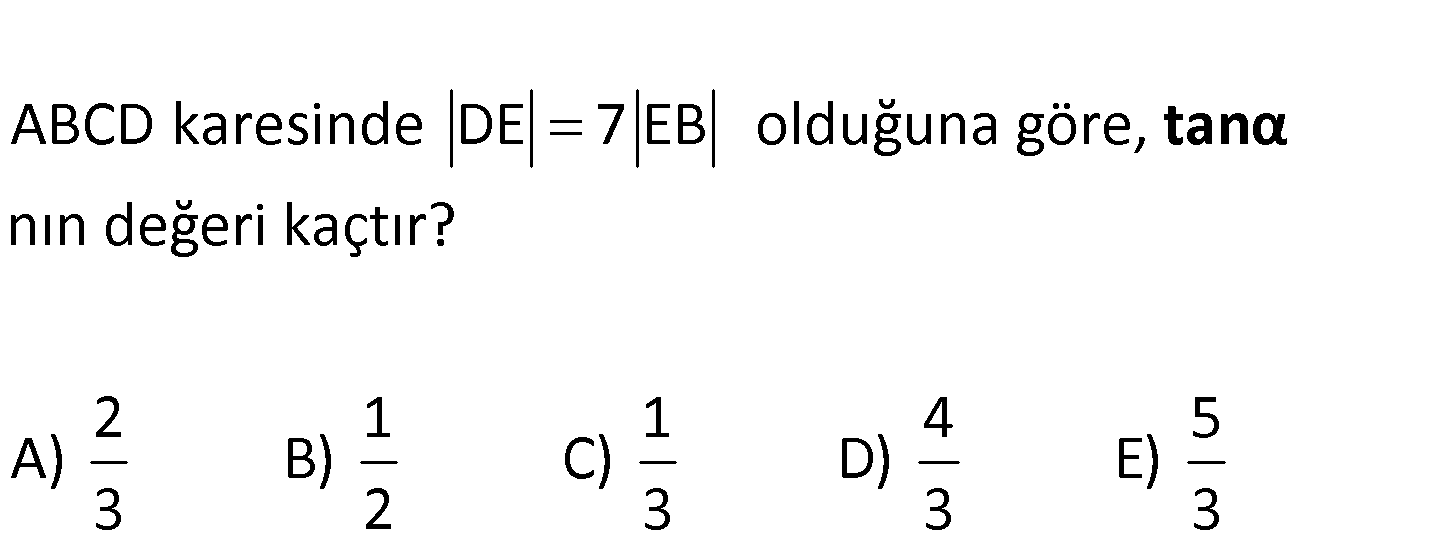

8.SORU


9.SORU

10.SORU

11.SORU


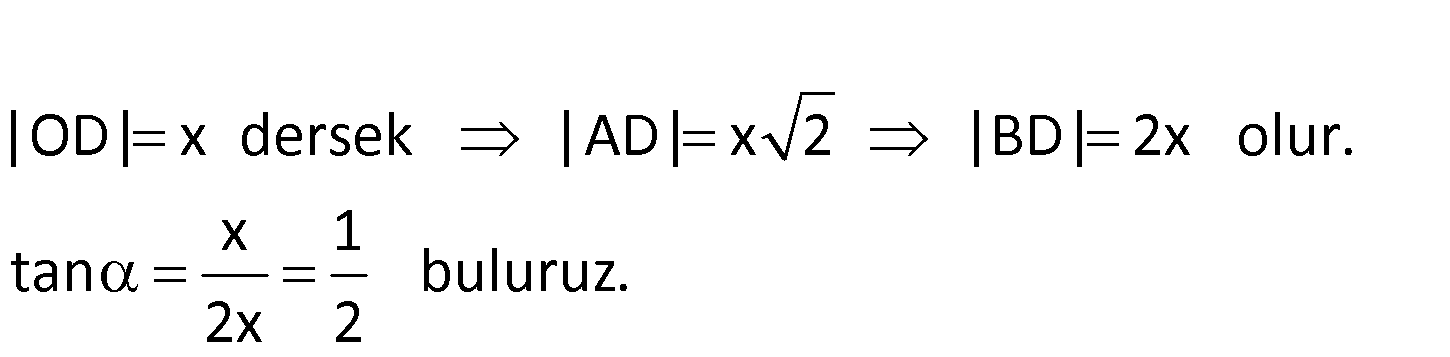
Diğer Soru Tipleri için Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
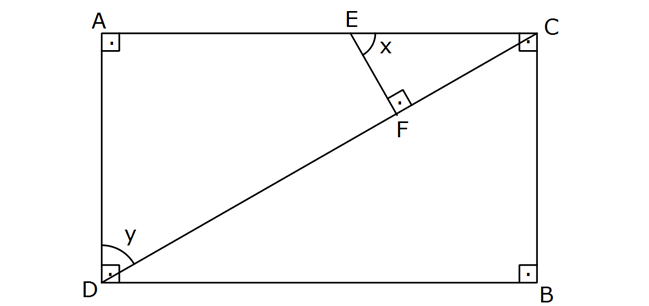
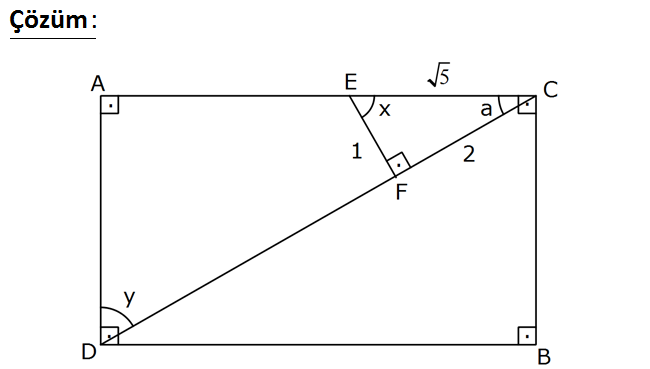
5 m(CEF) x , m(DAC) y ve cosecx 2 olduğuna göre, sec y kaçtır? www.matematikkolay.net DCA açısına a diyelim. ECF üçgenine göre x a 90 dir. DCA üçgenine göre de y a 90 dir. Buradan x y olduğunu görüyoruz. 5 1 5 2 cosecx ise sinx tir. 2 sinx 2 5 |FC| 2 dersek |EC| 5 olur. Pisagordan |EF| 1 buluruz. Buna göre; 1 1 sec y secx 5 buluruz. cosx 1 5 11
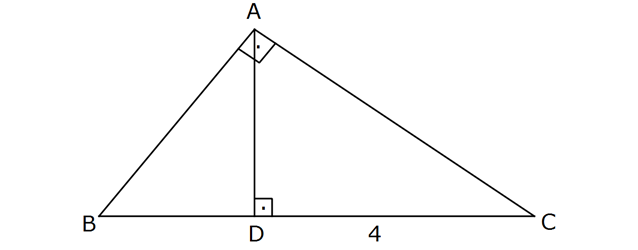
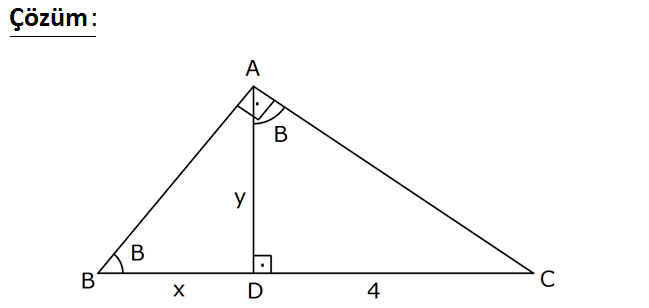
www.matematikkolay.net Yukarıdaki dik üçgende, CD 4 br olarak veriliyor. Buna göre, DB aşağıdakilerden hangisine eşittir? A 2 2 ) 4sinB B) 4tanB C) 4cot B D) 4tan B E) 4cotB m(BAD) 90 B olduğundan m(DAC) B dir. 4 4 DAC üçgeninde tanB y dir. y tanB BAD üçgeninde t 2 2 2 y anB y tanB x x y değerlerini eşitlersek; 4 tanB x tanB 4 1 x 4 4cot B buluruz. tan B tan B 14
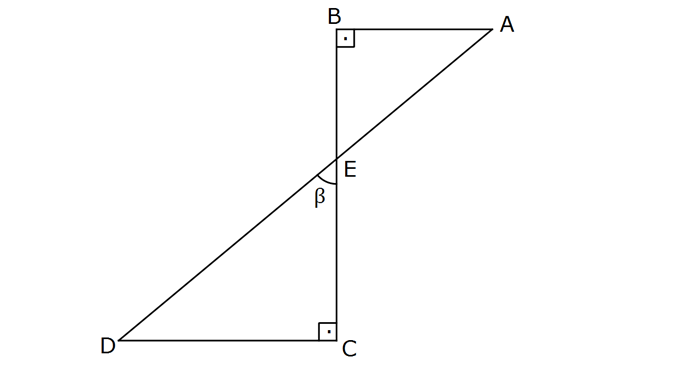
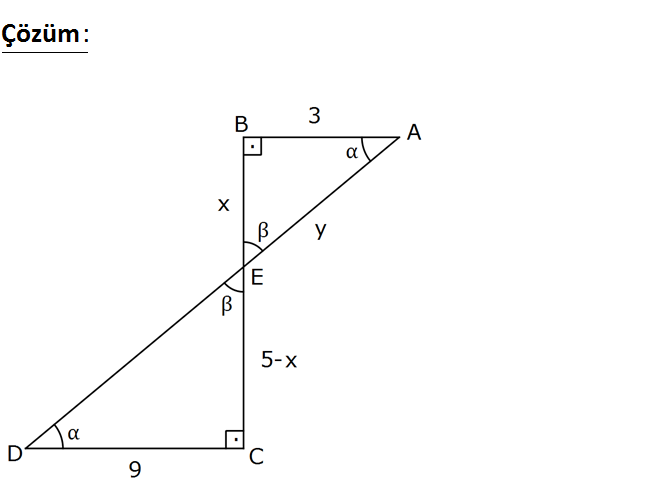
www.matematikkolay.net Şekilde [AB] / / [DE] , m(ABC) m(DCB) 90 AB 3 cm , DC 9 cm, BC 5 cm ve m(DEC) Buna göre, cos kaça eşittir? www.matematikkolay.net İki üçgen arasında benzerlik uygulaya m 3 : lı ; Çözüm 9 3 x 5 5 x 3x x tür. 5 x 4 5 Küçük üçgenin kenarları ,3, y olur. 4 1 Dikkat edilirse 5 12 13 üçgenini katı vardır. 4 13 Ohalde y olur. 4 5 x 4 5 cos buluruz. y 13 13 4 15
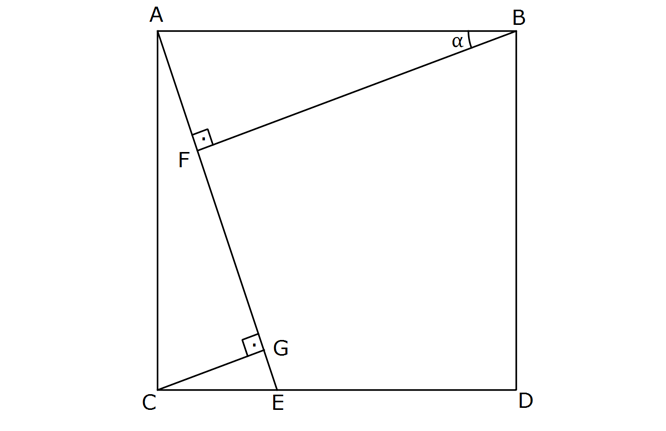
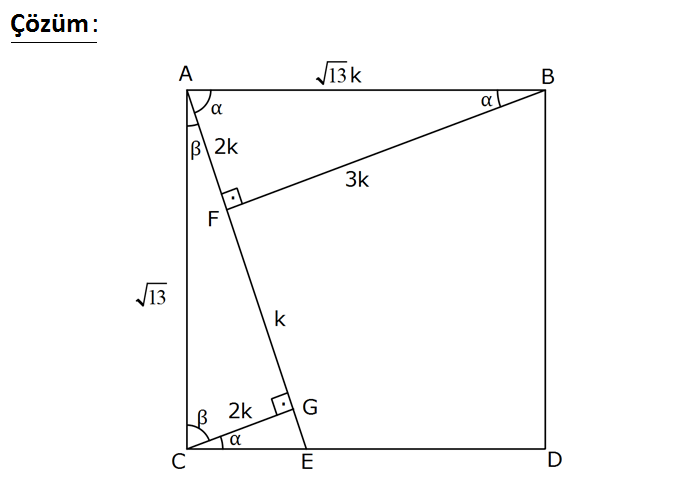
www.matematikkolay.net ABCD kare, [BA] [AE], [CG] [AE], AF 2 FG m(ABF) ise cosα = ? ACG ve AFB üçgenlerinin açıları eş ve hipotenüsleri aynı olduğundan eş üçgenlerdir.Oranları yerine yerleştirdiğimizde AB kenarı pisagordan 13k bulunur. 3k 3 cos bulunur. 13k 13 www.matematikkolay.net 19
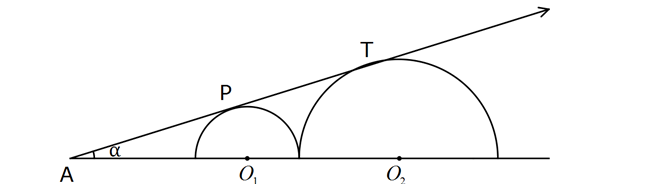
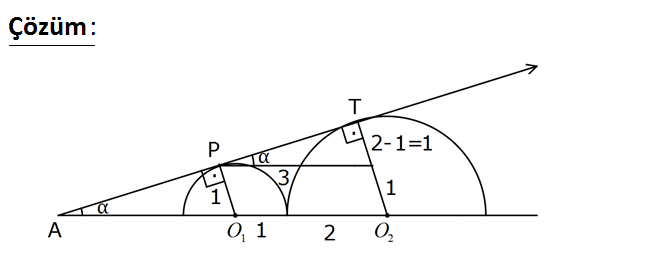
1 2 P ve T noktaları çembere teğet noktalardır. O merkezli çemberin yarıçapı O merkezli çemberin yarıçapının yarısıdır. Buna göre, sinα değeri kaçtır? Merkezden, teğet noktasına çizilen doğrular diktir. Bu diklikleri kullanarak, çemberler arasında şekildeki gibi bir üçgen oluşturabiliriz. Küçük çemberin yarıçapına 1, büyük çemberin yarı – çapına da 2 diyelim. açısını da şekildeki gibi üçgenin içine yazabiliriz. (yöndeş açılar). 1 O halde ; sin 3 buluruz. 20
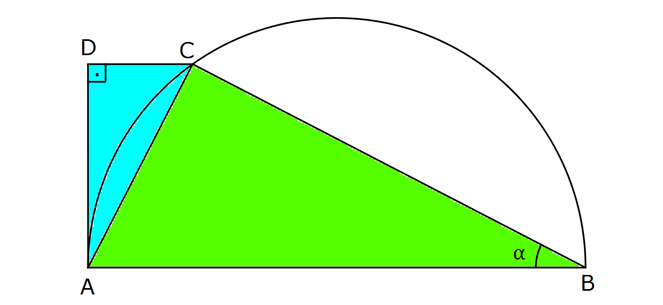
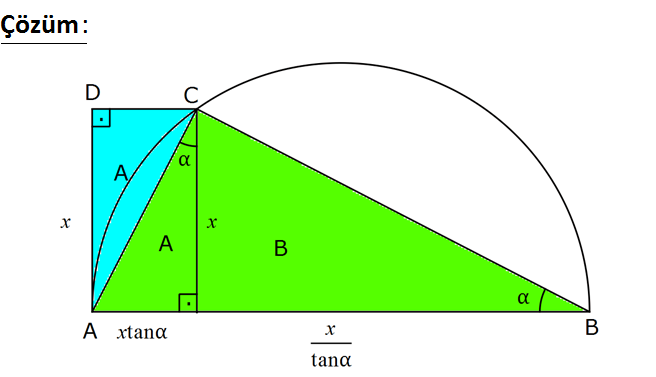
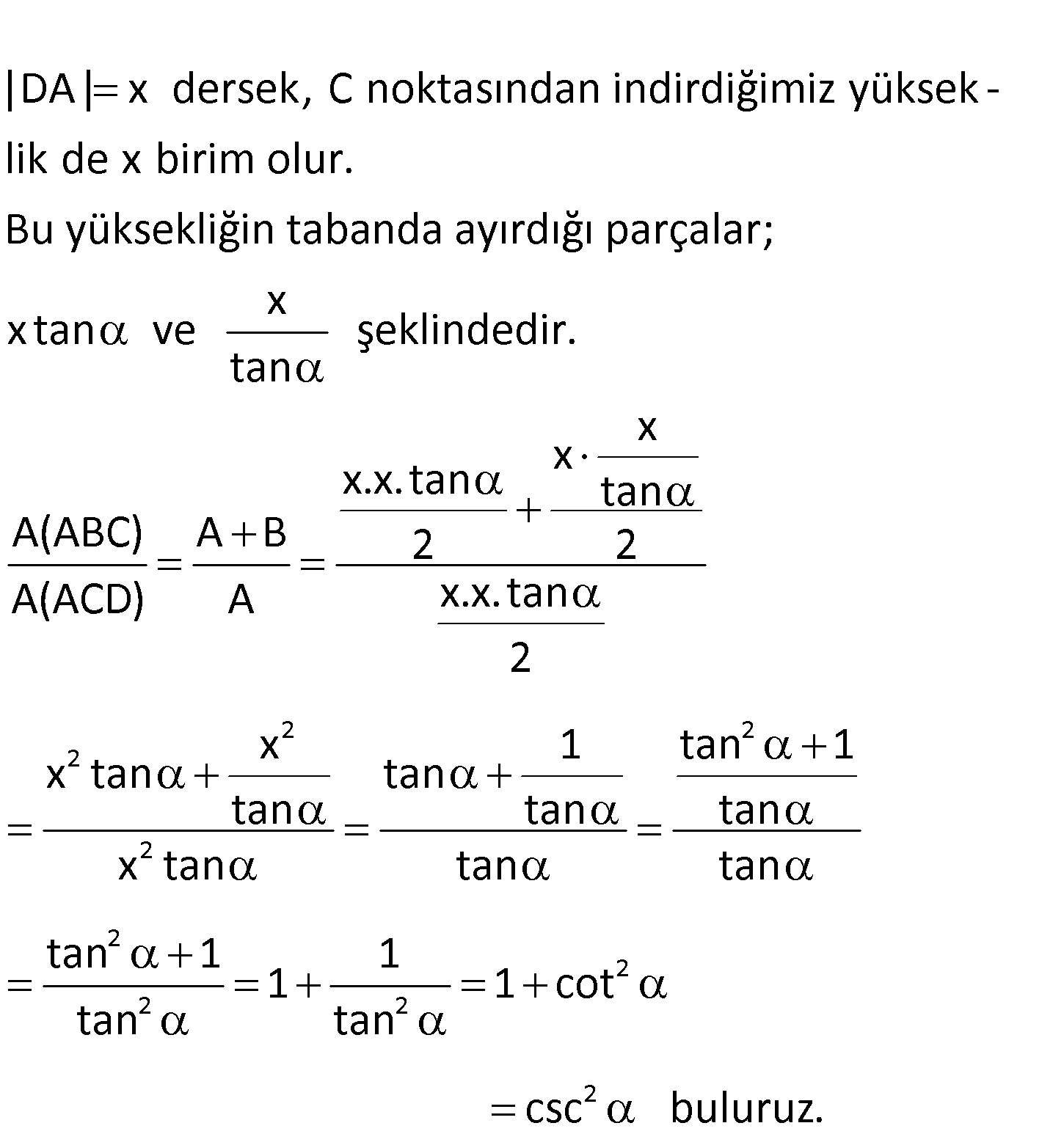
www.matematikkolay.net Yukarıdaki çemberin çapı [AB] , DA doğrusu çembe – re A’da teğet, AD DC , m(ABC) olduğuna göre, A( 2 2 2 2 2 aşağıdakilerden hangisine eşittir? A) sin B) cos C) csc D) tan E) sec ABC) A(ACD) www.matematikkolay.net |DA| x dersek, C noktasından indirdiğimiz yüksek – lik de x birim olur. Bu yüksekliğin tabanda ayırd 2 2 2 2 2 2 2 2 ığı parçalar; x x tan ve şeklindedir. tan x x x.x. tan tan A(ABC) A B 2 2 A(ACD) A x.x. tan 2 x 1 tan 1 x tan tan tan tan tan x tan tan tan tan 1 1 1 1 cot tan tan 2 csc buluruz. 35
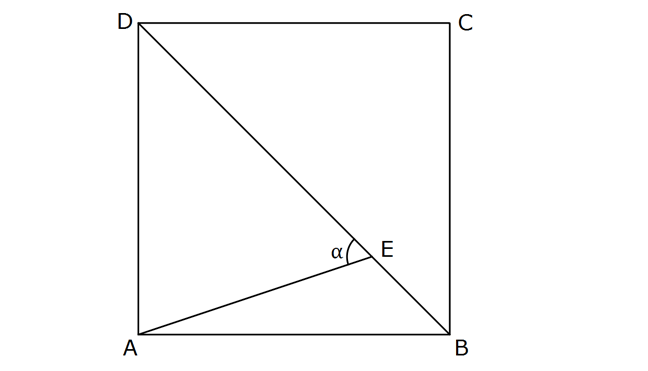
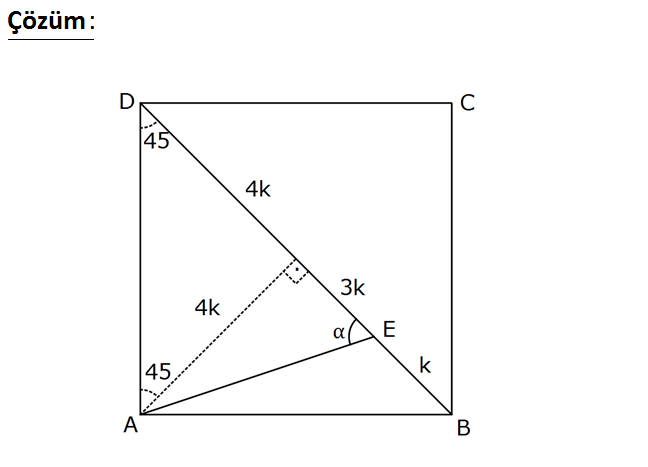
www.matematikkolay.net nın d A eğeri BCD karesi kaçtır? 2 1 1 4 5 A nde DE 7 EB olduğuna gör ) B) C) D) E) 3 2 3 3 e 3 , tanα www.matematikkolay.net ABCD karesinde DB köşegeni 8k olsun. AG zunluğunu indirirsek 45 45 90 üçgeni oluşur. AG 4k olur. GE 3k olur. 4k 4 tan bulunur. 3k 3 39
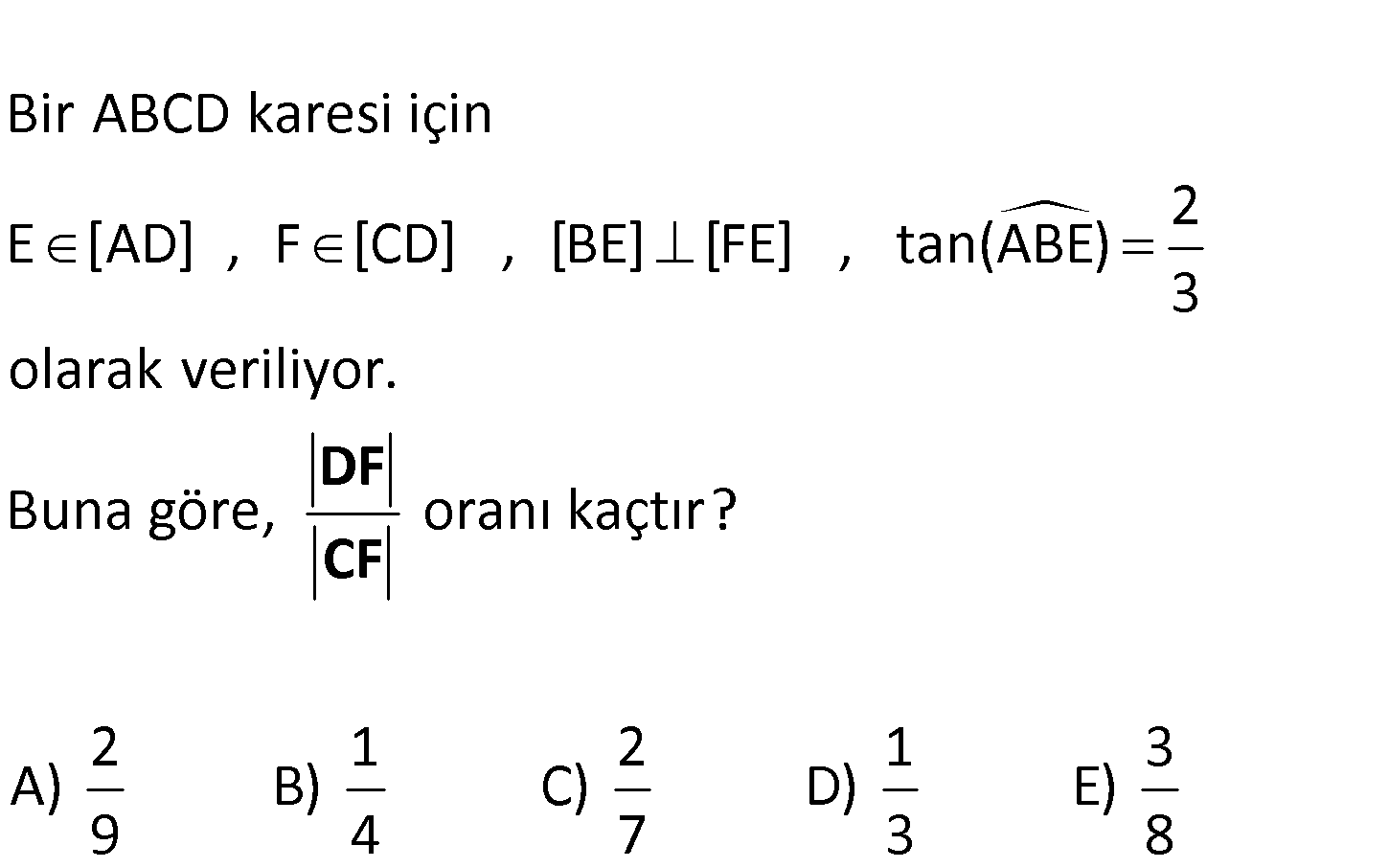
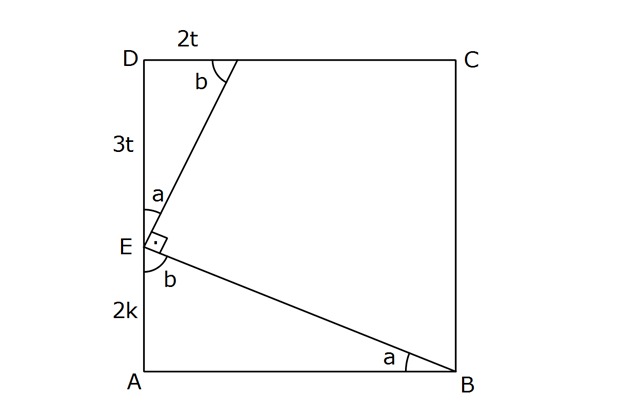
Bir ABCD karesi için 2 E [AD] , F [CD] , [BE] [FE] , tan(ABE) 3 olarak veriliyo Buna gör , r. e D oranı kaçtır? 2 1 2 1 3 A) B) C) D) E) 9 4 7 3 8 F CF Kareyi tanımda olduğu gibi çizelim. m ABE a olsun. m AEB b olsun. m DEF a olur. 2 tan A : BE AE 2k, AB 3 Çözüm 3k olsun. Aynı şekilde; 2 tan DEF DE 3t, DF 2t olsun. 3 www.matematikkolay.net Karenin tüm kenarları birbirine eşit olduğundan; 3t 2k 3k 3t k dır. AB 3k 3.3t 9t CF 9t 2t 7t dir. DF 2t 2 bulunur. CF 7t 7 40
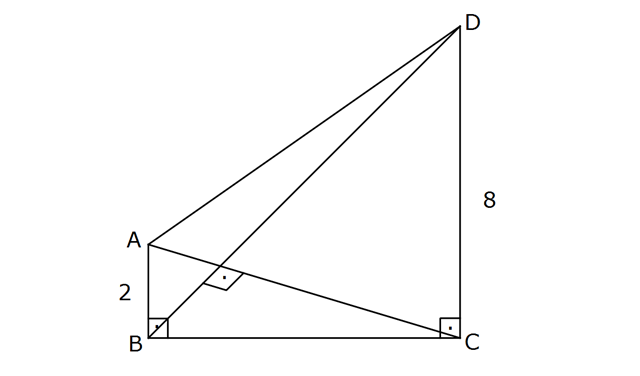
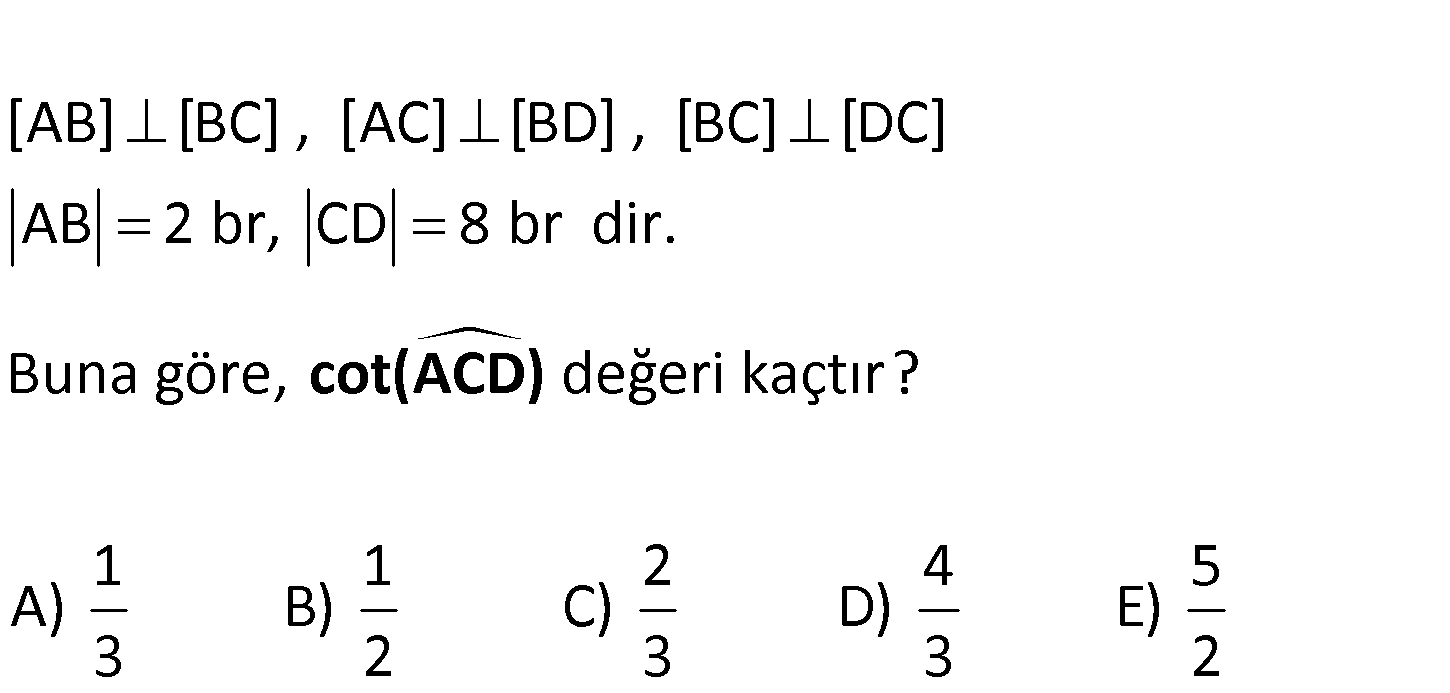
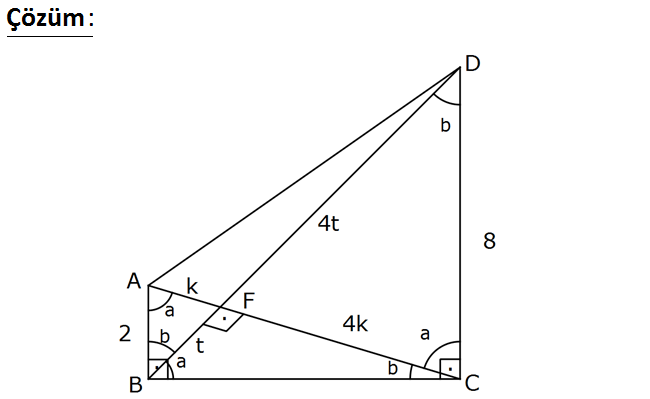
www.matematikkolay.net [AB] [BC] , [AC] [BD] , [BC] [DC] AB 2 br, CD 8 Buna göre, değeri kaçtır? 1 A) B) b 3 r dir. cot(ACD) 1 2 4 5 C) D) E) 2 3 3 2 www.matematikkolay.net Açıları a ve b diye harflendirdikten sonra, ABF üçgeni ile CDF üçgeni arasında benzerlik uygulayabi 2 2 2 liriz. Hipotenüsler arasında 4 kat oran var, BF t FD 4t ve AF k FC 4k diyebiliriz. DBC üçgeninde öklitten, (4k) t.4t 16k 4t t 2k buluruz. t 2k 1 cot(ACD) cota buluruz. 4k 4k 2 41
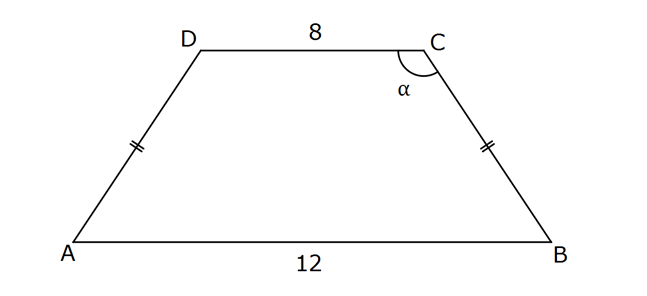
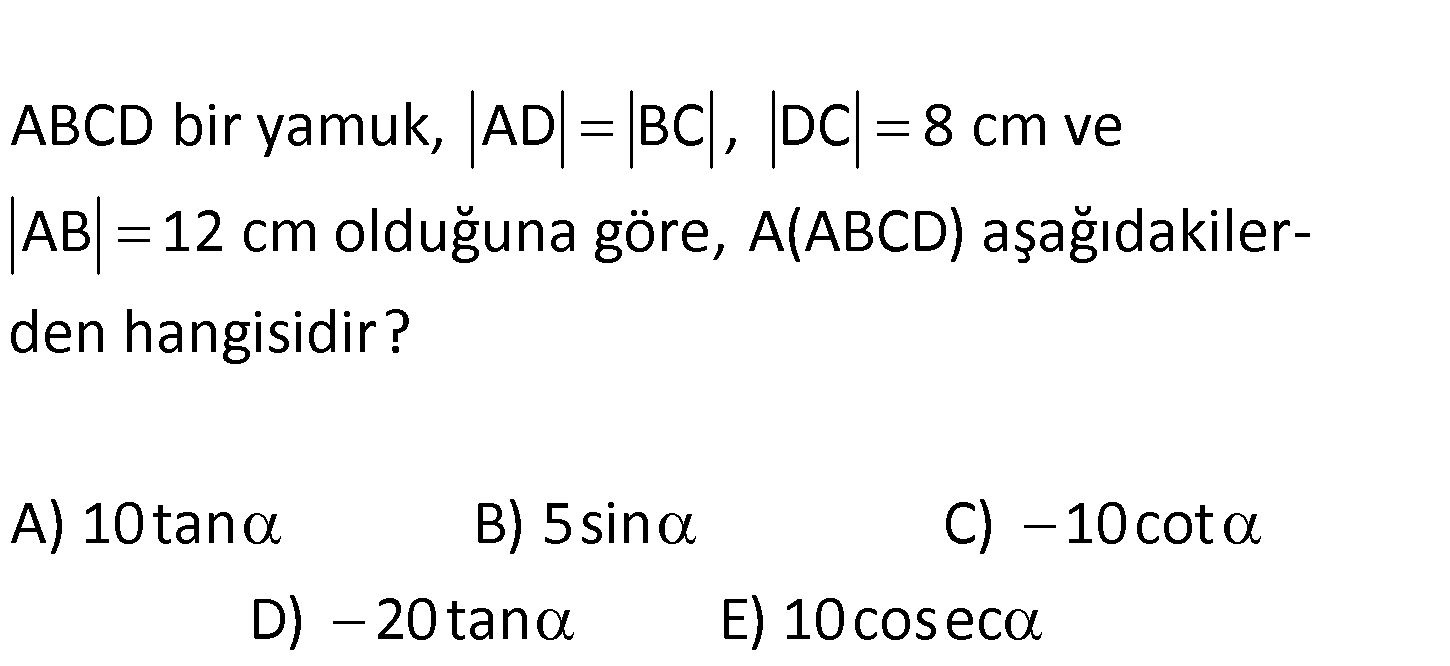
www.matematikkolay.net ABCD bir yamuk, AD BC , DC 8 cm ve AB 12 cm olduğuna göre, A(ABCD) aşağıdakilerden hangisidir? A) 1 0tan B) 5sin C) 10cot D) 20tan E) 10cosec www.matematikkolay.net İkizkenar bir yamuk olduğundan tabana şekildeki dikmeler indirdiğimizde yanda kalan dik üçgenlerin kenarları 2’şer cm olur. h tan 180 dir. 2 Not : tan 180 tan dır. h tan 2 2tan h dır. 8 12 Yamuğun alanı h 10h 10 2 tan 2 20tan dır. 62
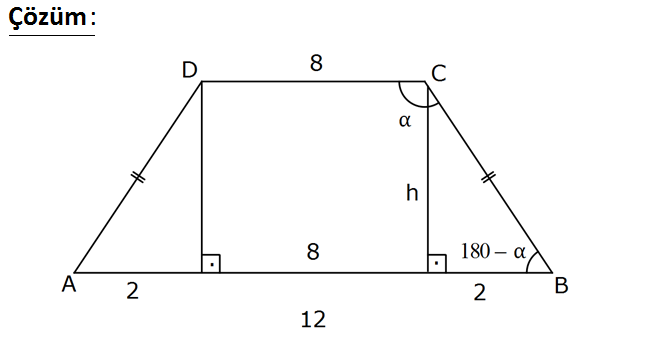
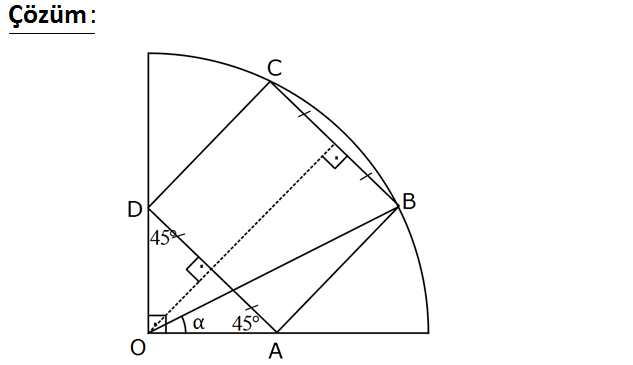
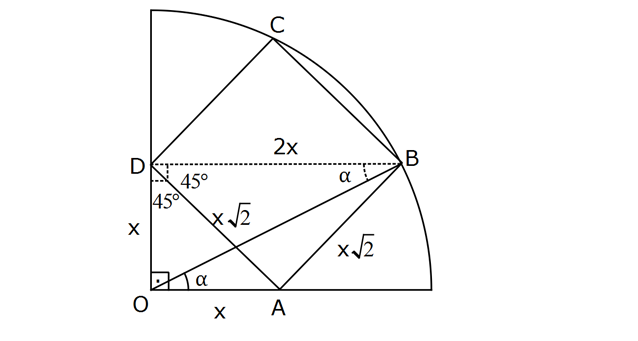
Yukarıdaki şekilde O merkezli çeyrek çember ve ABCD karesi verilmiştir. m(BOA) olduğuna göre, ta kaçtır? 1 1 1 A) B) C) D) 1 E) 2 3 2 nα www.matematikkolay.net Merkezden [BC] kirişine dikme indirirsek, iki eşit parçaya böler. Karenin diğer kenarı olan [AD] de , [BC]’ye paralel ve eşit olduğundan iki eşit parçaya bölünecektir. OAD üçgeninde yüksekliğin tabanı iki eşit parçaya böldüğünü görüyoruz. Buna göre OAD üçgeni bir ikizkenar dik üçgendir ve açıları 45-45-90 şeklindedir. |OD| x dersek |AD| x 2 |BD| 2x olur. x 1 tan buluruz. 2x 2 126


Efso sorular seviliyosunuz