Soru Sor sayfası kullanılarak Logaritma konusu altında Yaklaşık değer bulma, Ondalık Kısmı Bulma, Logaritma Basamak Sayısı Bulma ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU

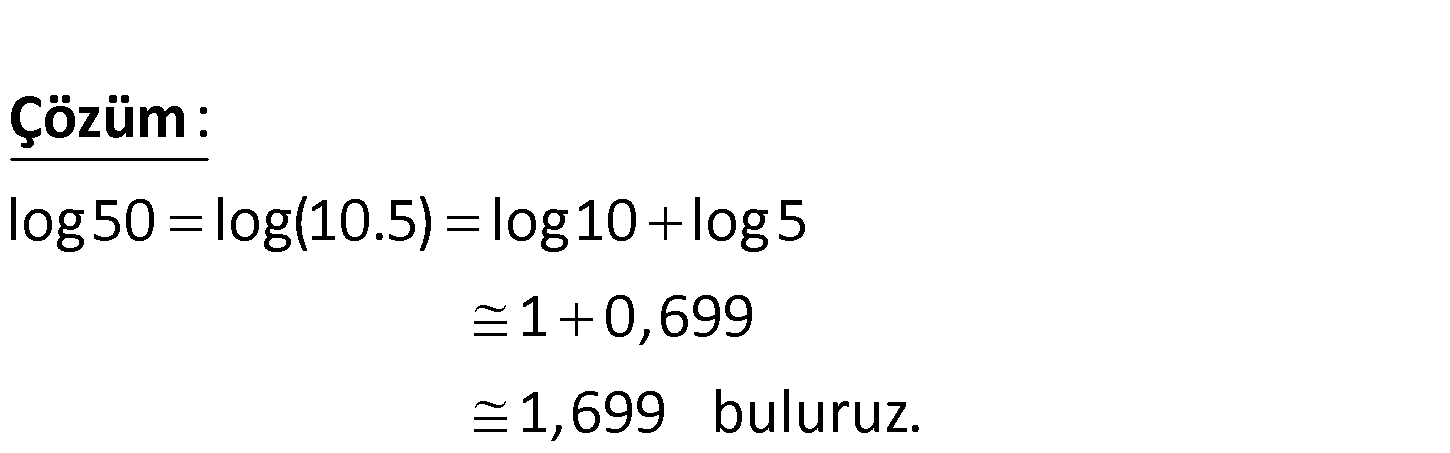
2.SORU

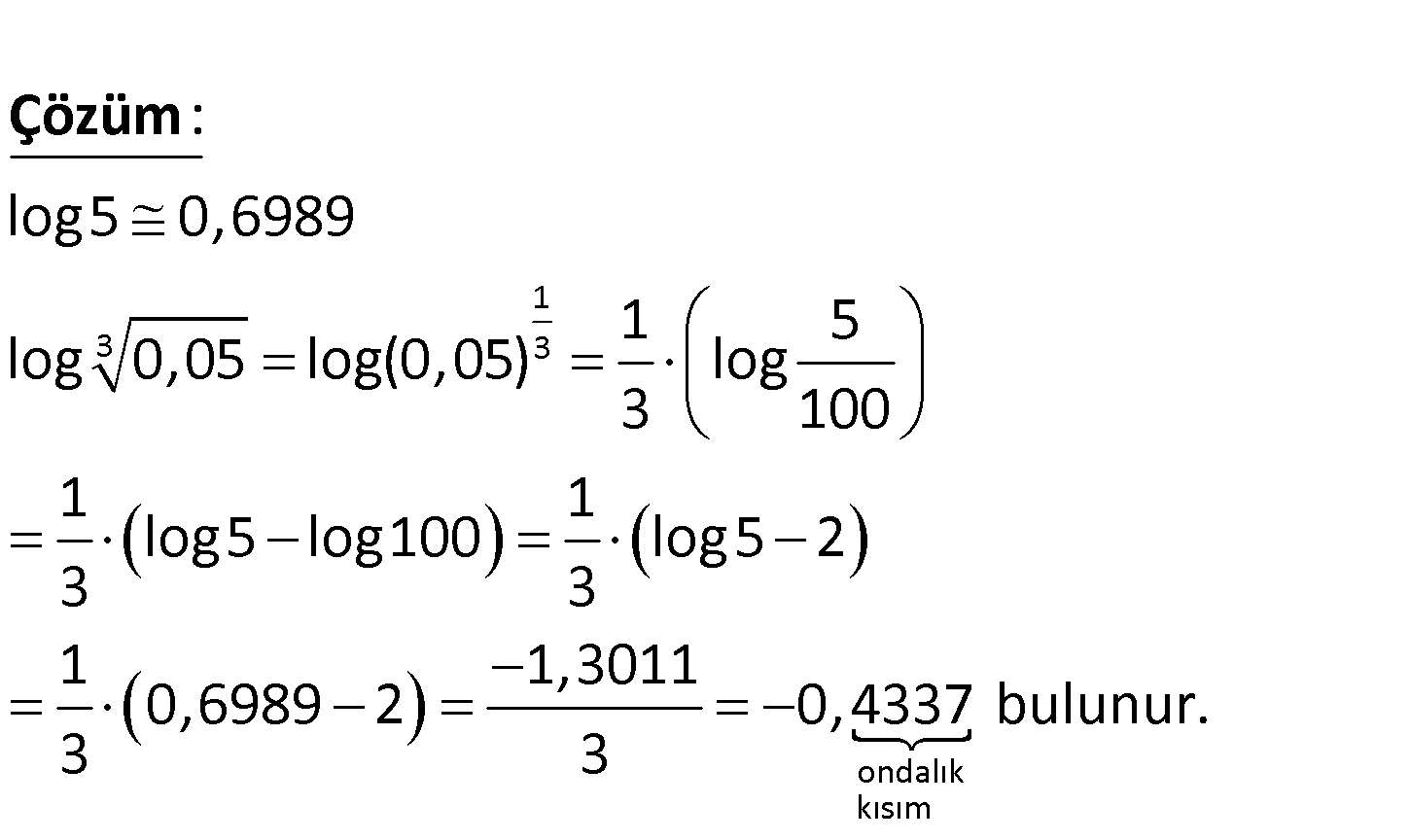
3.SORU


4.SORU


Diğer Soru Tipleri için Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
log5 0,699 olduğuna göre, log 50 nin yaklaşık değeri kaçtır? A) 0,301 B) 1,301 C) 1,699 D) 2,189 E) 2,301 log50 log(10.5) log10 log5 1 0,699 : Çözüm 1,699 buluruz. 45
3 log5 0,6989 olduğuna göre, log 0,05 sayısının ondalık kısmı aşağıdakilerden hangisine eşitti r? A) 5663 B) 4337 C) 337 D) 663 E) 63 1 3 3 log5 0,6989 1 5 log 0,05 log(0,05) log 3 100 1 1 log5 log100 log5 2 3 3 1 1,301 0,6989 : 2 3 Çözüm ondalık kısım 1 0,4337 bulunur. 3 81
20 log2 0,301 log3 0,477 olduğuna göre, 18 sayısı kaç basamaklıdır? 20 2 log18 20log18 20log(3 .2) 20.(2log3 log2) 20.(2.0, : 4 Çözüm 77 0,301) 20.(0,954 0,301) 20.(1,255) 25,1 dir. Basamak sayısı da, 25’in 1 fazlası olacaktır. 26 www.matematikkolay.net 59
x bir tam sayı olmak üzere 2,7 logx 11,3 olduğuna göre, x sayısının basamak sayısının al abileceği değerlerin toplamı kaçtır? A) 63 B) 68 C) 75 D) 77 E) 81 www.matematikkolay.net 2,7 11,3 2 3 2,7 2,7 logx 11,3 ise 10 x 10 tür. 10 100 , 10 1000 dir. 10 değeri b : u iki sayın Çözüm 11,3 2,7 ın arasındadır. Yani 3 basamaklı bir sayıdır. 10 değeri de benzer şekilde 12 basamaklı bir sayıdır. 3 basamaklı bir sayı x 12 basamaklı bir sayı x sayısı 3 basamaklı olup da 10 den büyük olabilir. Ö 2,7 rneğin 10 501 küsür olsun. x 600 olarak da bu eşitsizliği sağlar. Aynı şekilde x sayısı 12 basamaklı da olabilir. x 3,4,5,…,12 basamaklı olabiliyorsa 12 3 12 3 15 Toplarsak 1 10 2 1 2 75 buluruz. 149

