Soru Sor sayfası kullanılarak Logaritma konusu altında Logaritma Tanım Aralığı ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
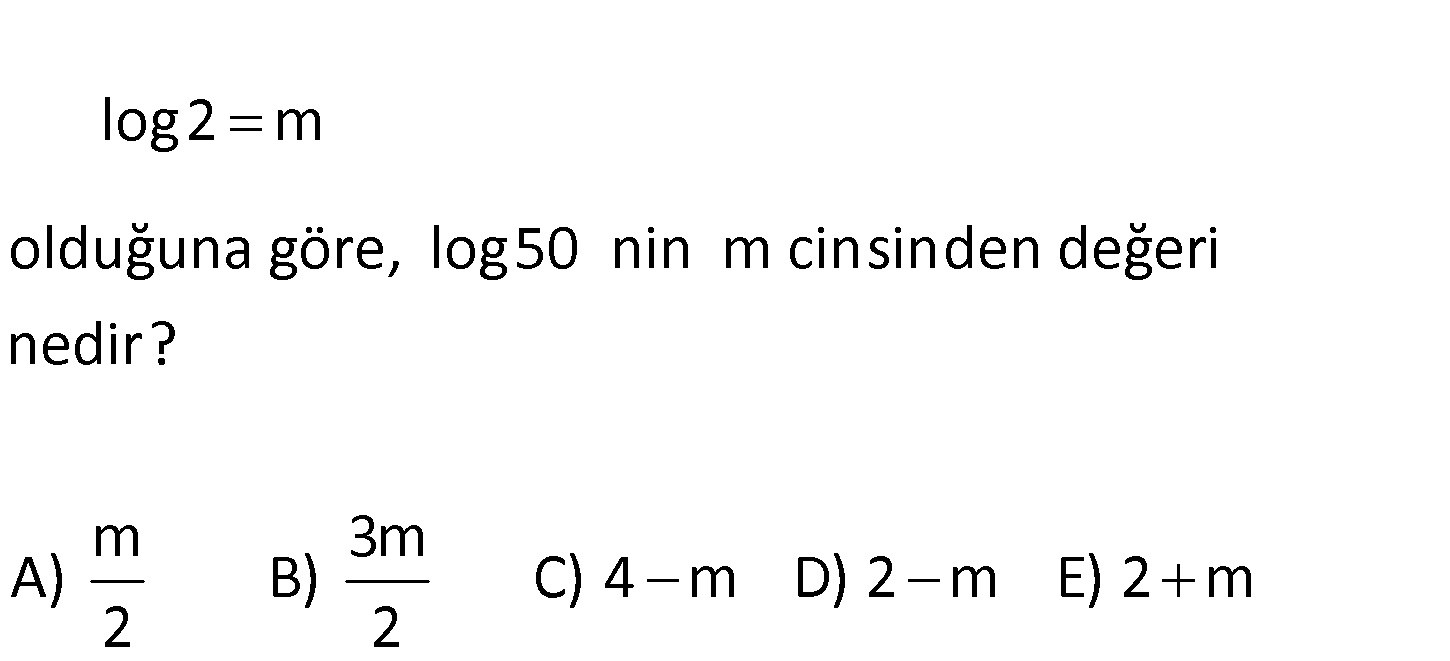
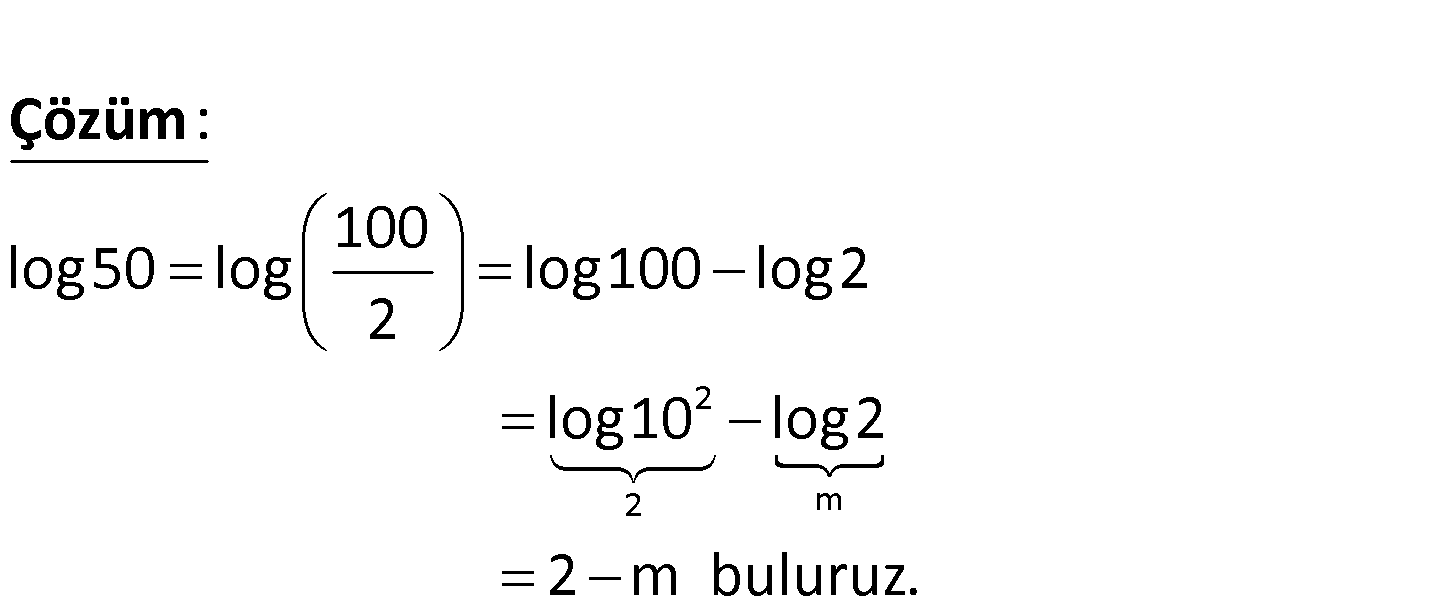
2.SORU
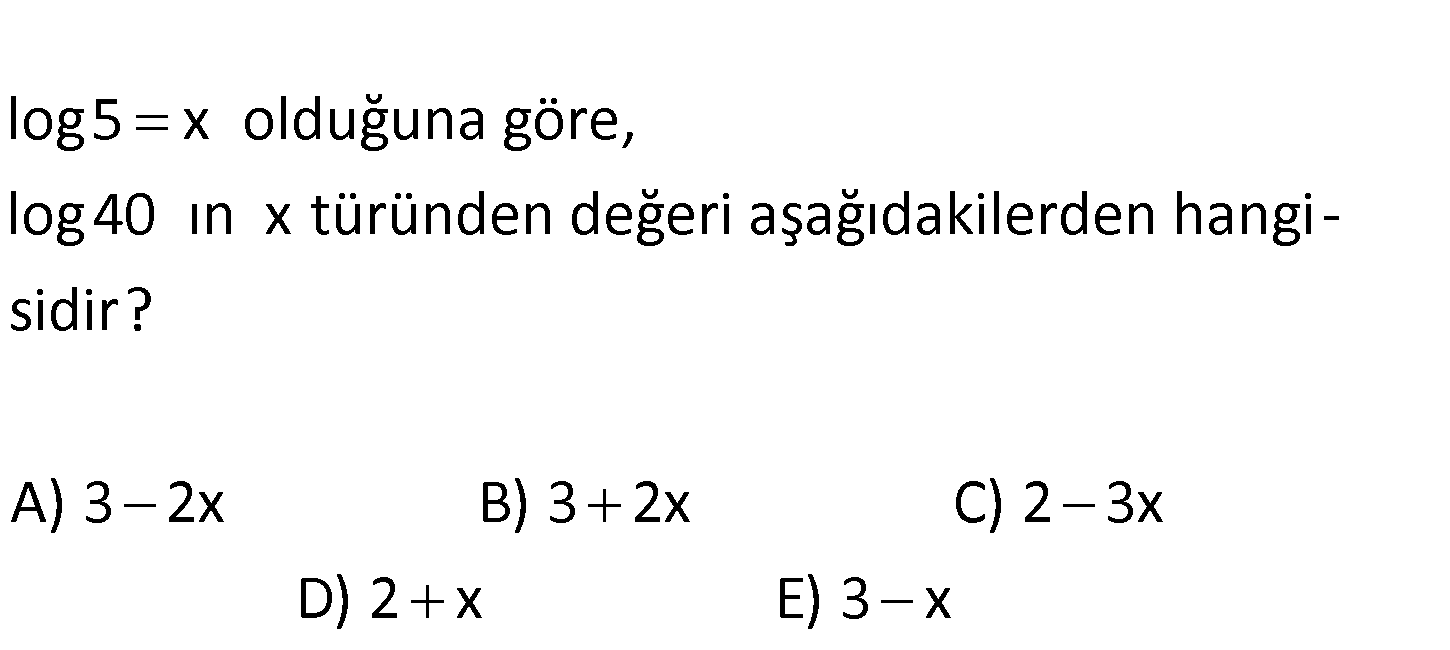

3.SORU
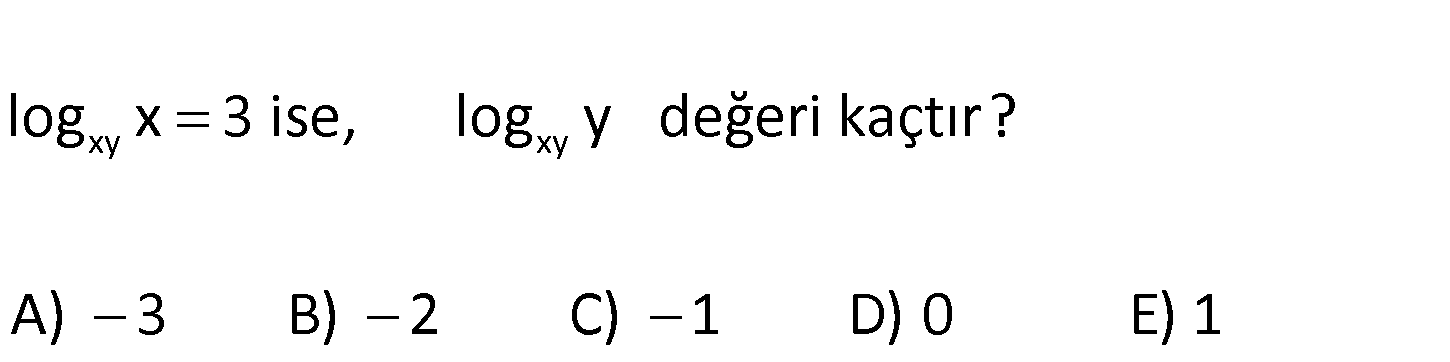

4.SORU
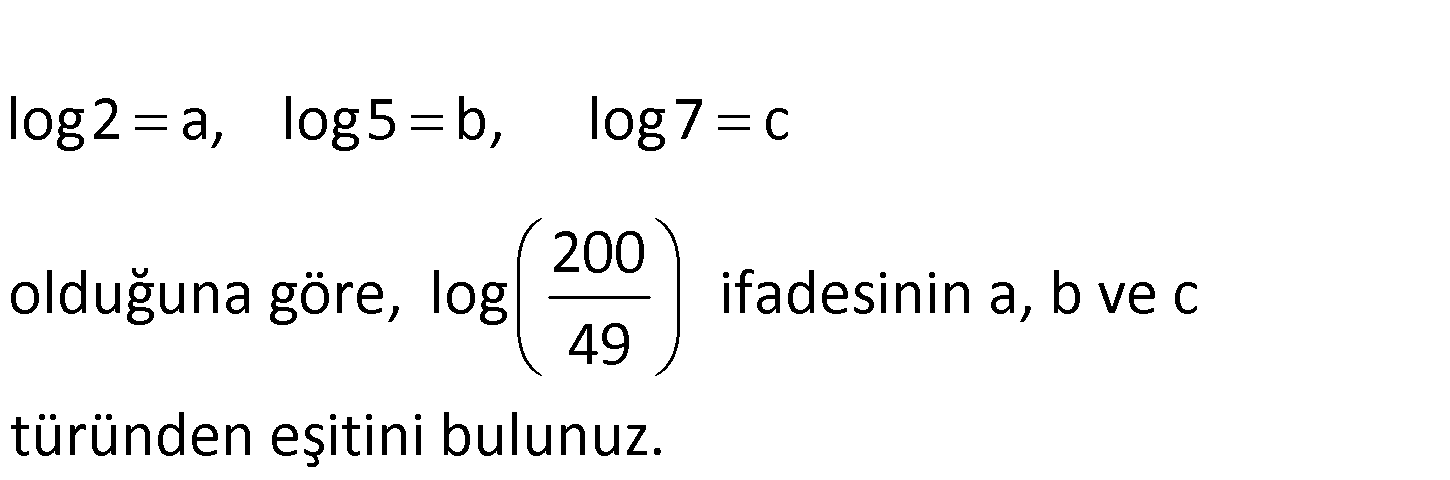

5.SORU
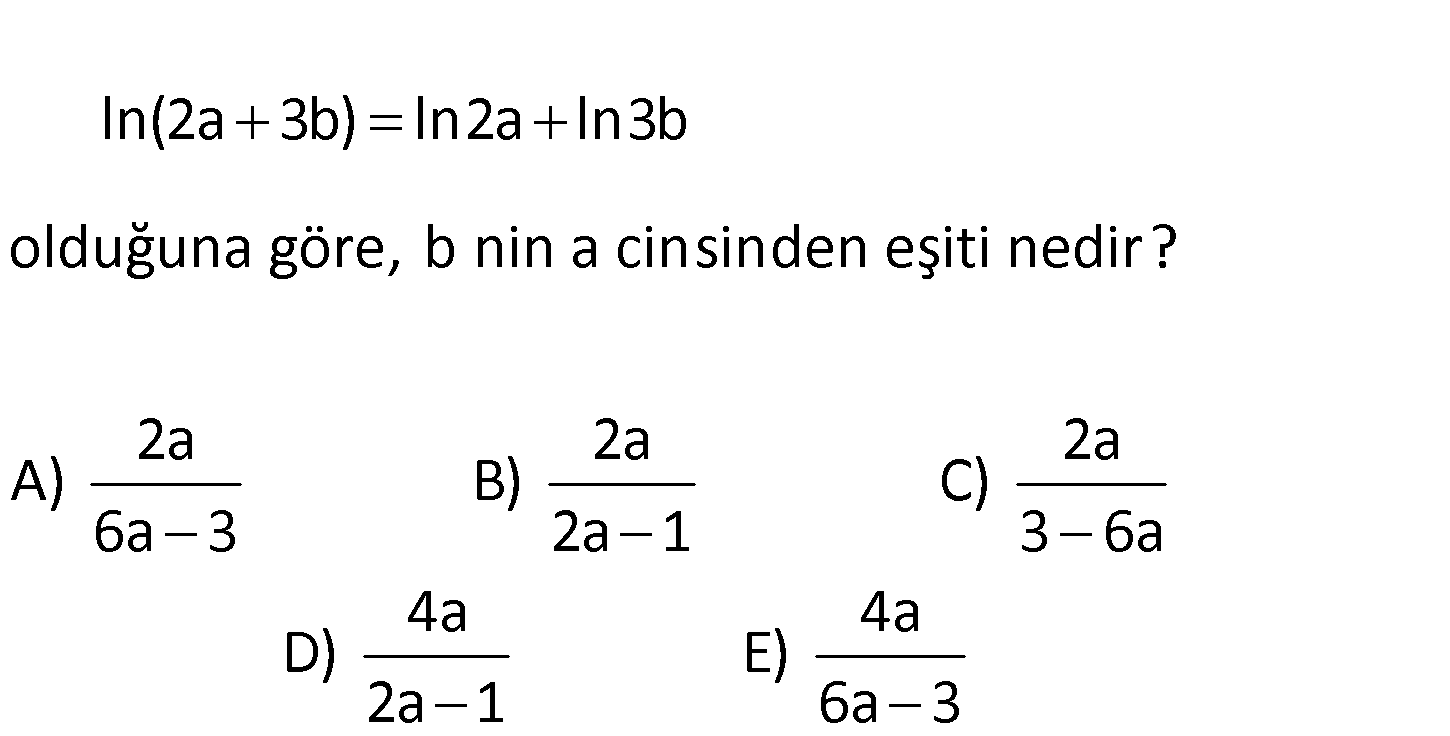

6.SORU

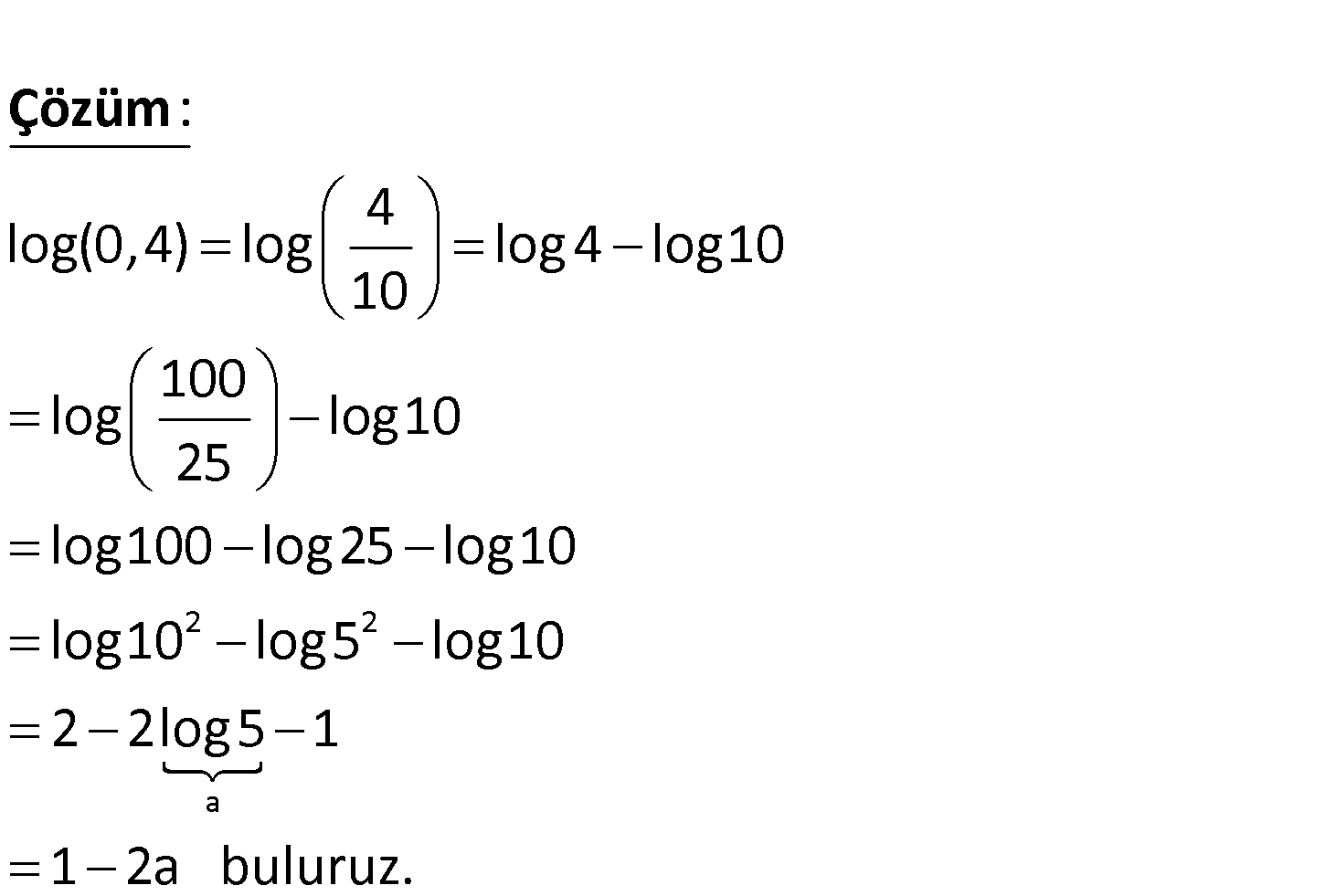
7.SORU
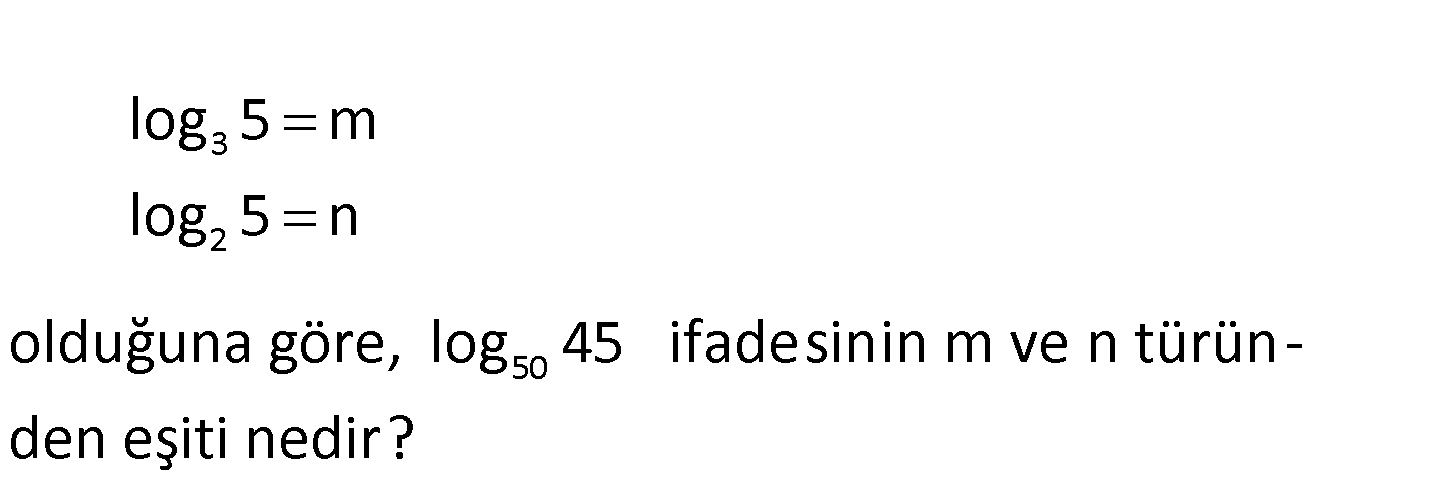
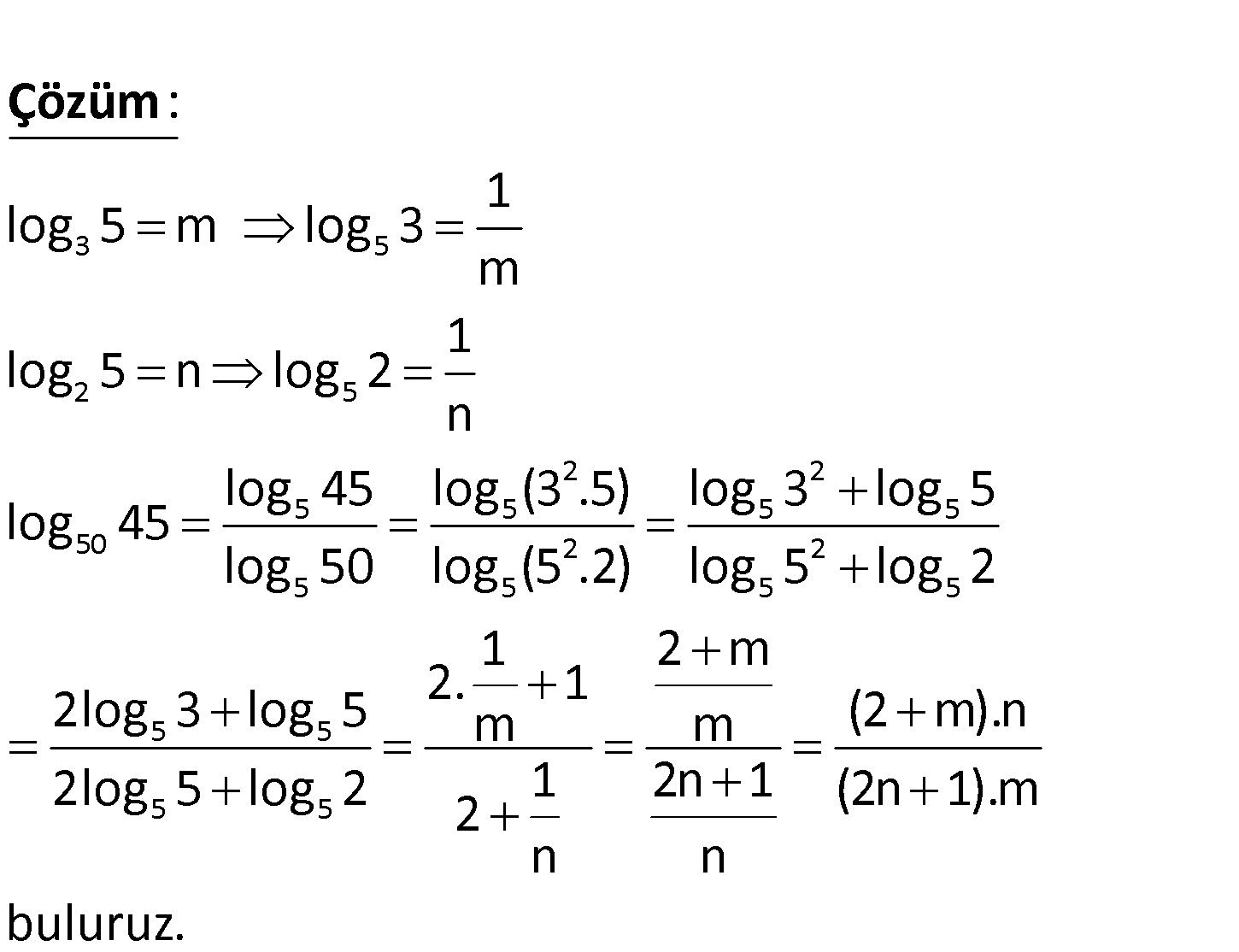
8.SORU
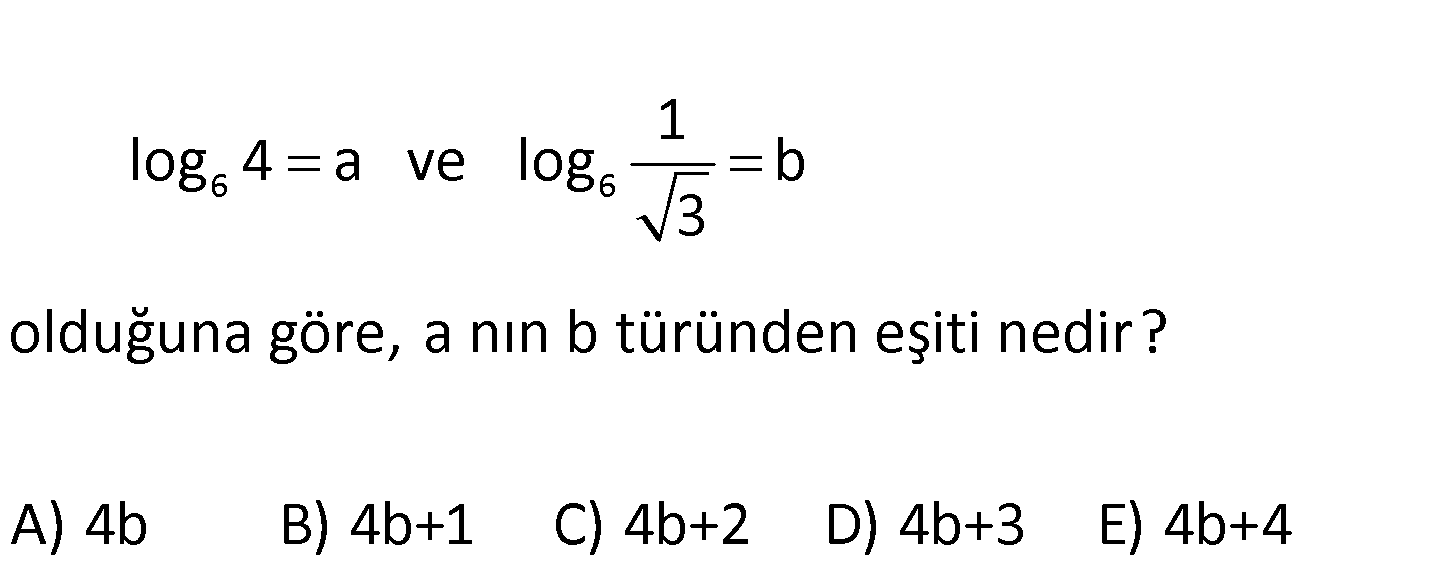
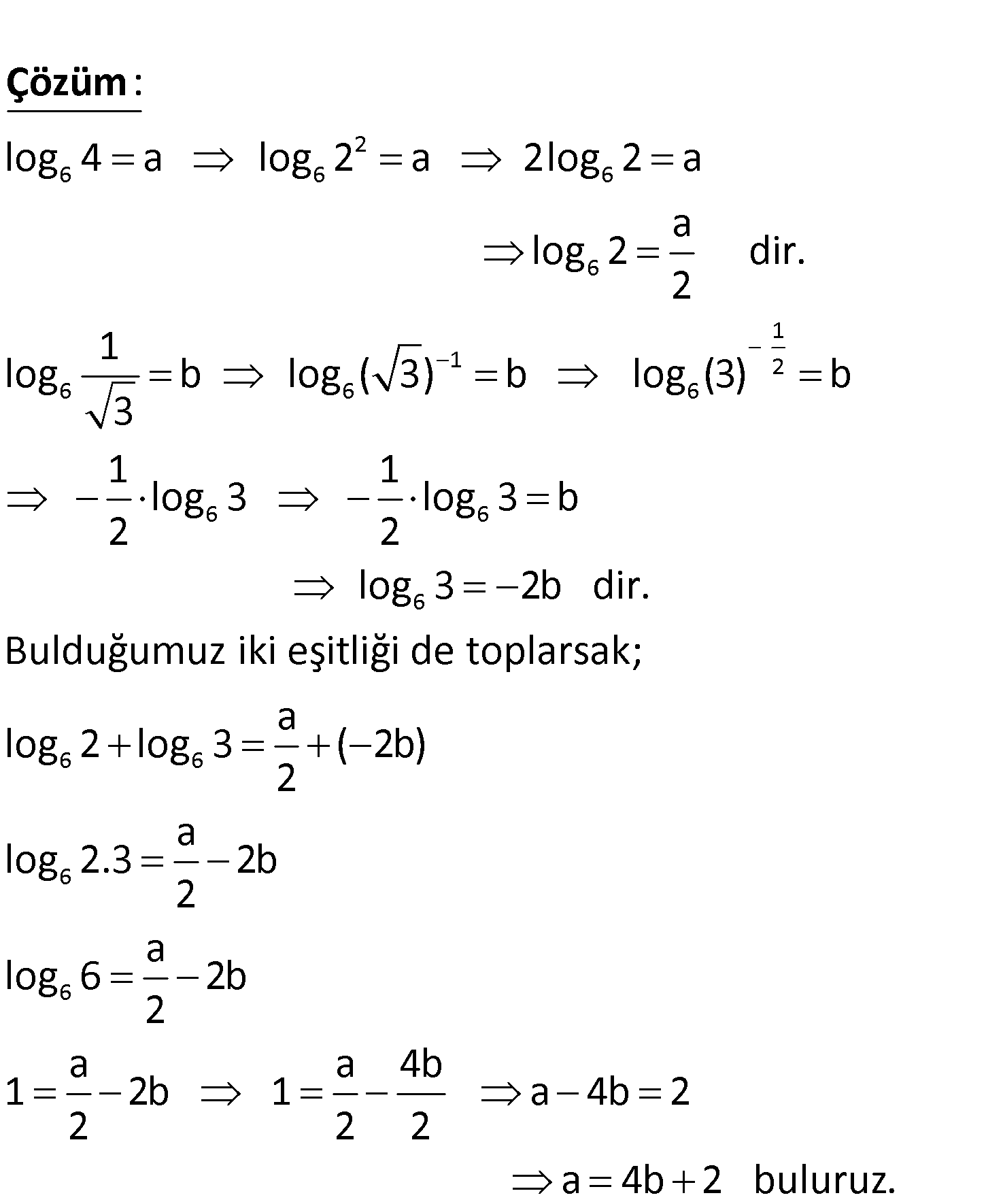
9.SORU
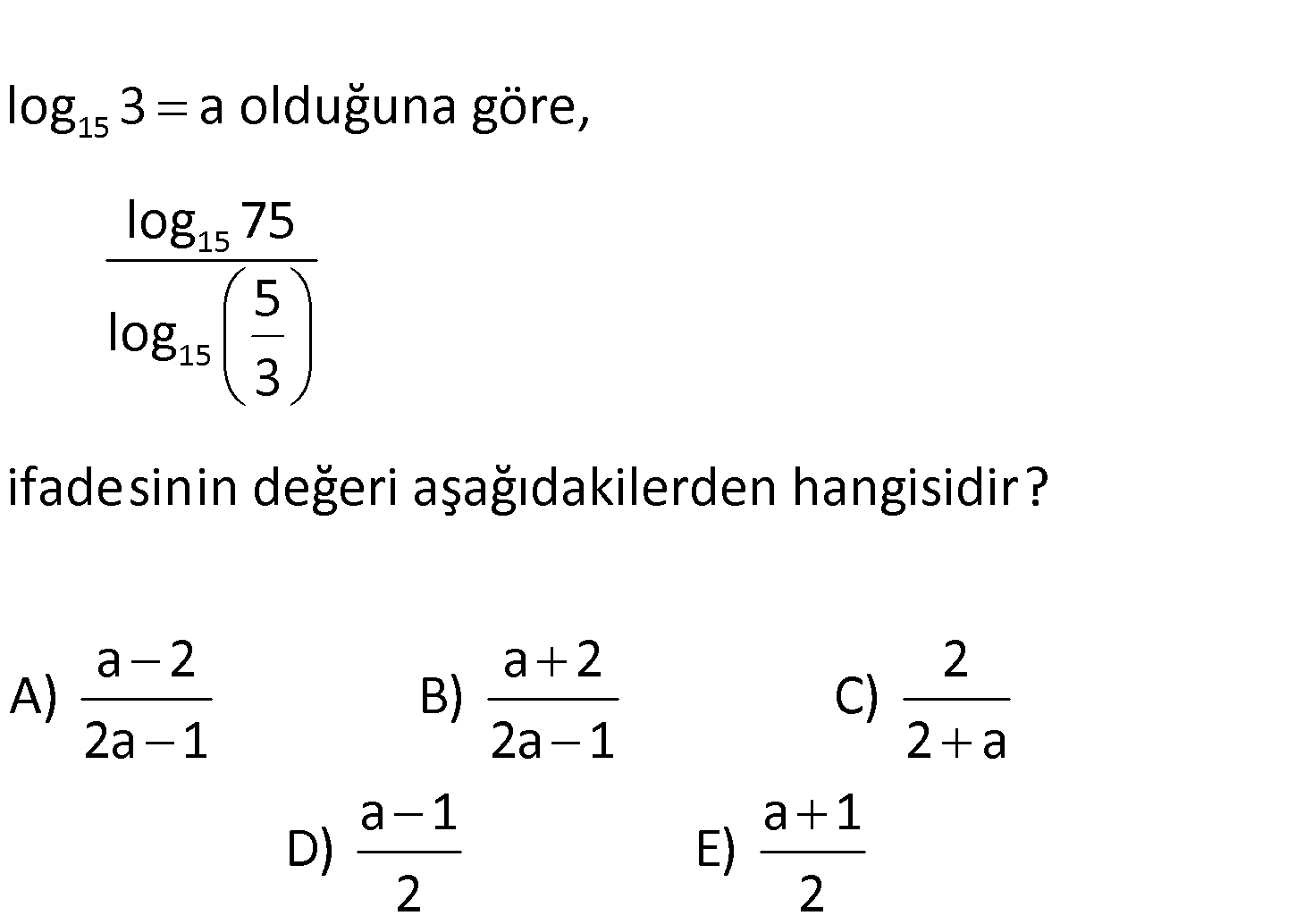
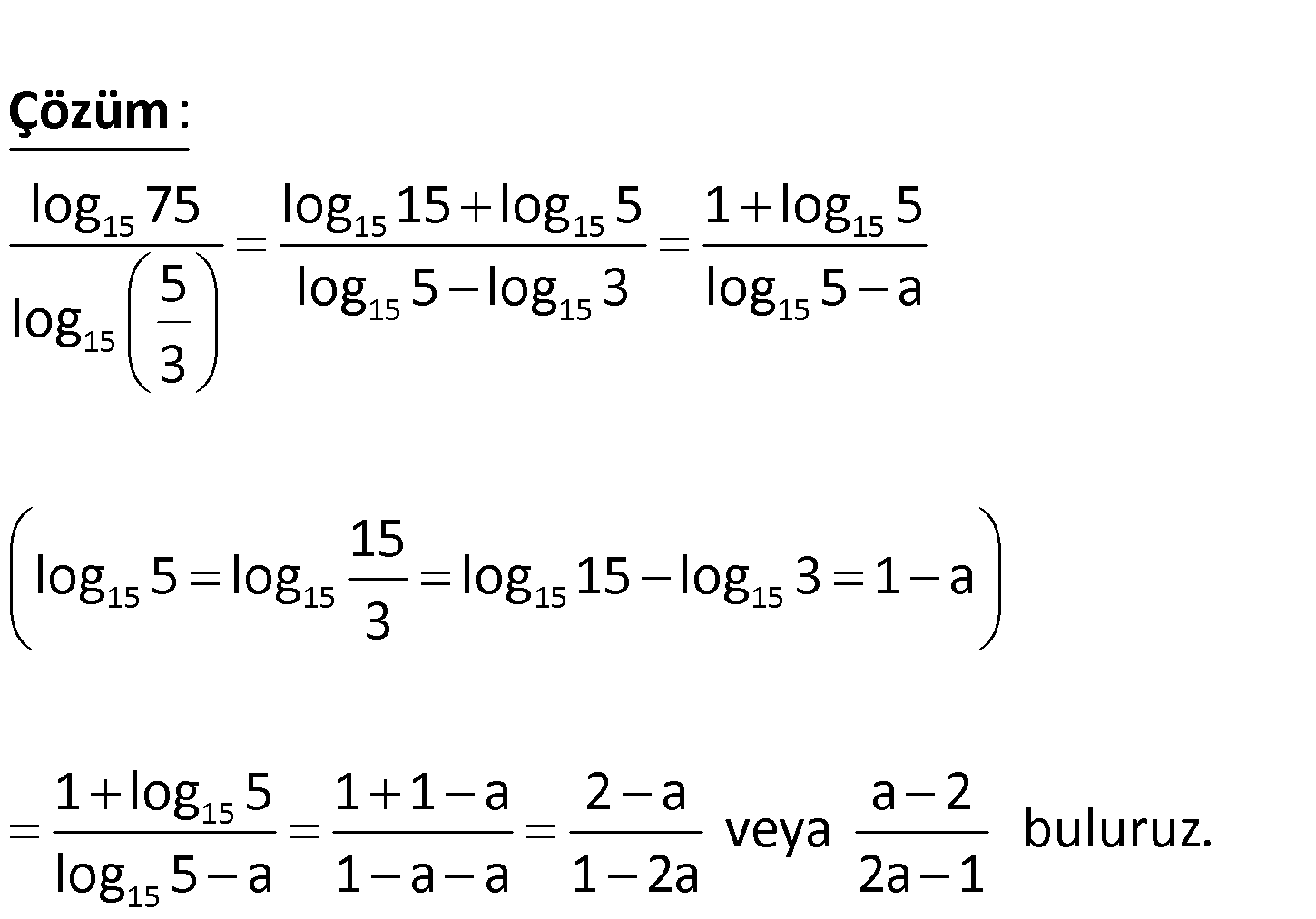
10.SORU

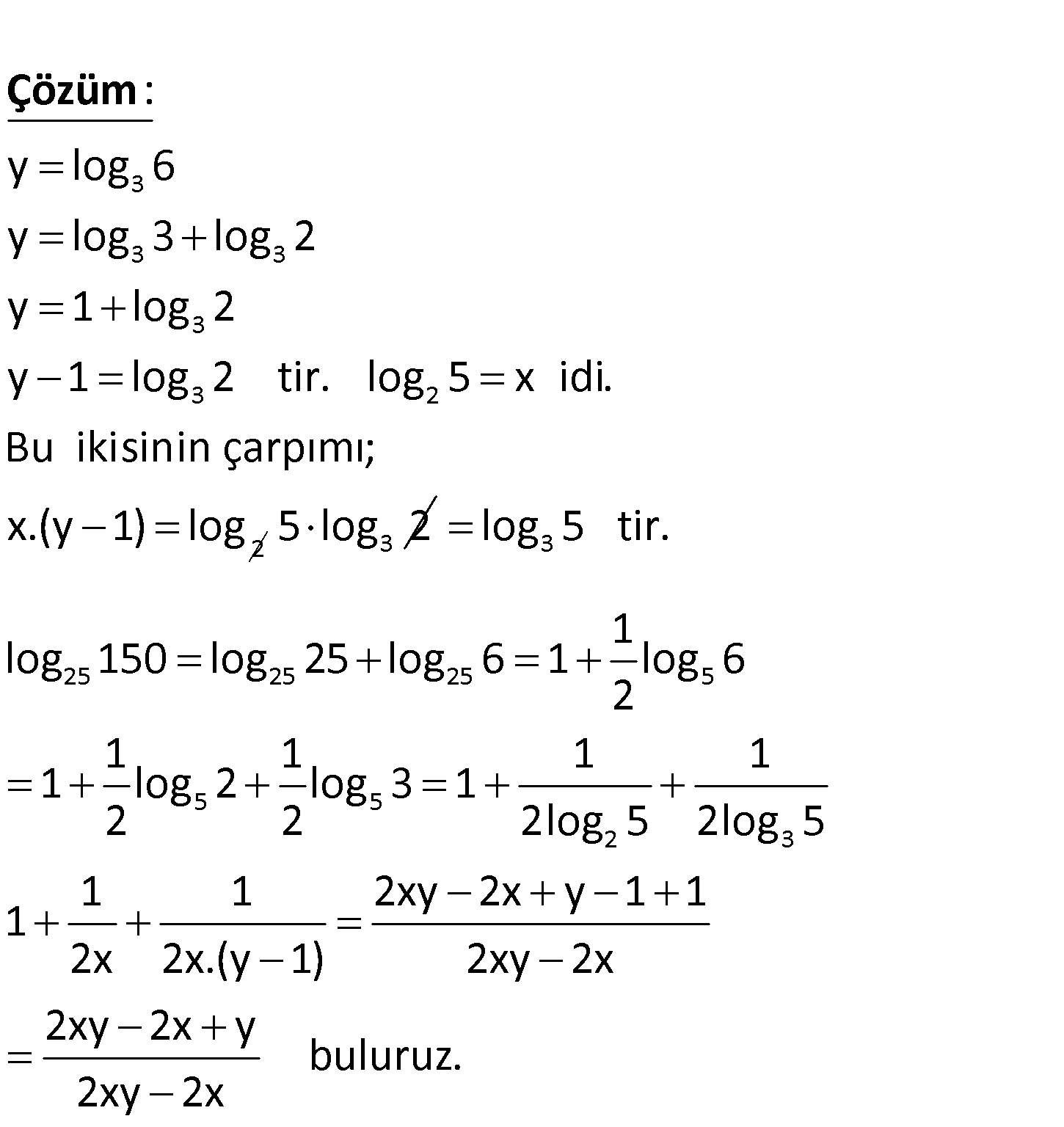
11.SORU
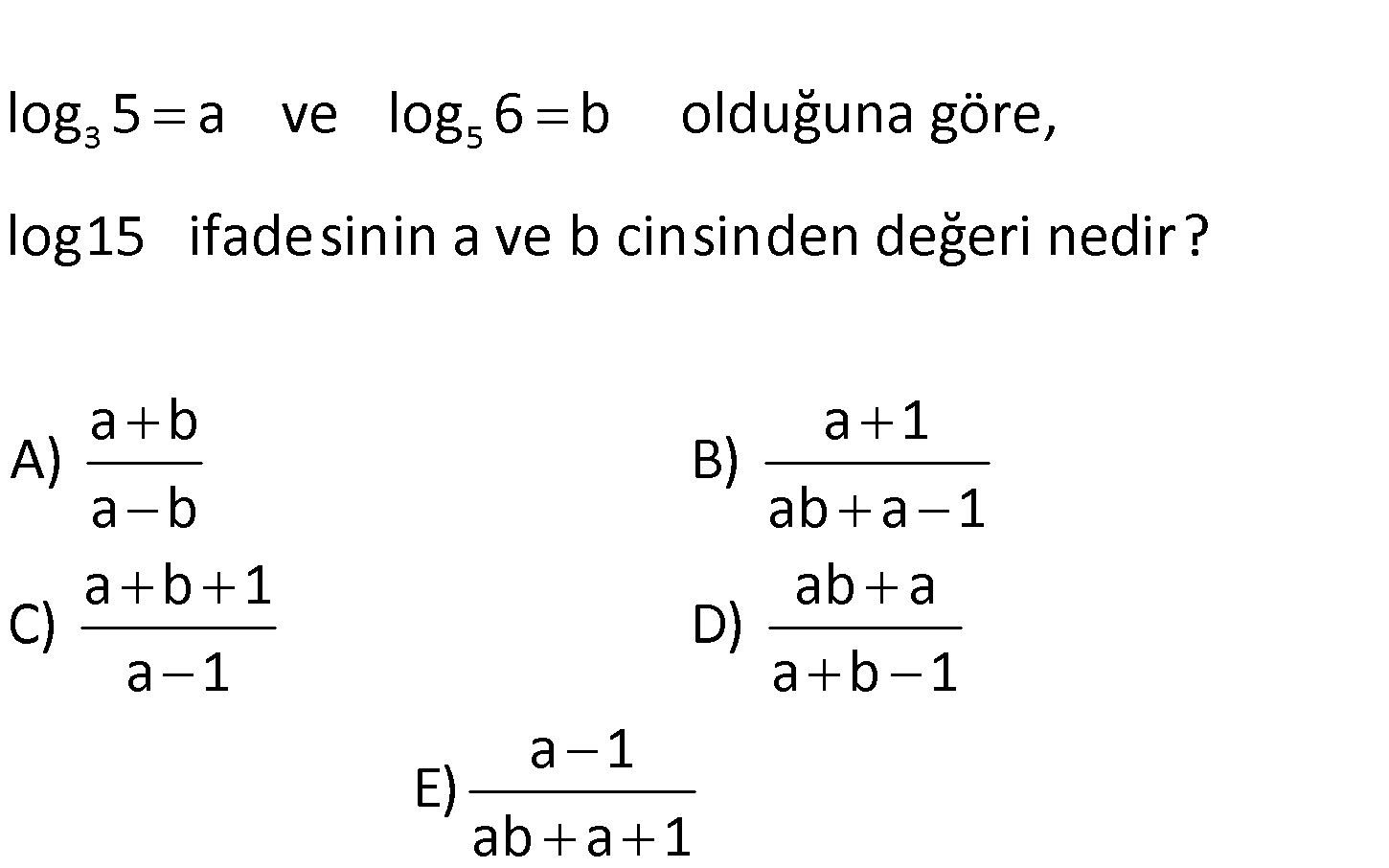

Diğer Soru Tipleri için Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
log2 m olduğuna göre, log 50 nin m cinsinden değeri nedir? m 3m A) B) C) 4 m D) 2 m E) 2 m 2 2 2 2 m 100 log50 log log100 log2 2 log10 log2 : Çözüm 2 m buluruz. 18
log5 x olduğuna göre, log40 ın x türünden değeri aşağıdakilerden hangi – sidir? A) 3 2x B) 3 2x C) 2 3x D) 2 x E) 3 x www.matematikkolay.net 2 log40 log(4.10) log4 log10 log4 1 log2 1 2log2 1 10 2log 1 5 2(log10 log5) 1 2(1 x) 1 2 : Çözüm 2x 1 3 2x buluruz. 22
xy xy log x 3 ise, log y değeri kaçtır? A) 3 B) 2 C) 1 D) 0 E) 1 xy xy xy xy xy 3 xy İki ifadeyi de toplayalım. log x log y log (xy) 1 dir. log x log y 1 ise 3 log y 1 lo : g Çözüm xy xy y 1 3 log y 2 buluruz. www.matematikkolay.net 6
log2 a, log5 b, log7 c 200 olduğuna göre, log ifadesinin a, b ve c 49 türünden eşitini bulunuz. 2 3 2 3 2 200 log log200 log49 49 log(8.25) log7 log(2 .5 ) 2log7 log(2 ) log(5 ) 2log7 3log : 2 2lo Çözüm g5 2log7 3log2 2log5 2log7 3a 2b 2c buluruz. 27
ln(2a 3b) ln2a ln3b olduğuna göre, b nin a cinsinden eşiti nedir? 2a 2a 2a A) B) C) 6a 3 2a 1 3 6a 4a 4a D) E) 2a1 6a3 www.matematikkolay.net ln(2a 3b) ln2a ln3b ln(2a 3b) ln(2a.3b) 2a 3b 6ab 2a 6ab 3b 2a 3b(2a 1) 2a 3b 2a 1 2a b bulur 6a 3 : Çözüm uz. 13
log5 a olduğuna göre, log(0,4) ifadesinin eşiti aşağıdaki – lerden hangisidir? A) 3 a B) 1 a C) 12a D) 12a E) 2a2 2 2 4 log(0,4) log log4 log10 10 100 log log10 25 log100 log25 log10 log10 log5 lo 10 : g Çözüm a 2 2log5 1 1 2a buluruz. 39
3 2 50 log 5 m log 5 n olduğuna göre, log 45 ifadesinin m ve n türünden eşiti nedir? 3 5 2 5 2 2 5 5 5 5 50 2 5 5 5 1 log 5 m log 3 m 1 log 5 n log 2 n log 45 log (3 .5) log 3 log 5 log 45 log 50 log (5 .2) lo 5 : g Çözüm 2 5 5 5 5 5 log 2 1 2 m 02.Oca 2log 3 log 5 m m (2 m).n 2log 5 log 2 1 2n 1 (2n 1).m 2 n n buluruz. www.matematikkolay.net 57
6 6 1 log 4 a ve log b 3 olduğuna göre, a nın b türünden eşiti nedir? A) 4b B) 4b+1 C) 4b+2 D) 4 b+3 E) 4b+4 2 6 6 6 6 log 4 a log 2 a 2log 2 a a log 2 : 2 Çözüm 1 1 2 6 6 6 6 6 6 6 6 6 6 dir. 1 log b log ( 3) b log (3) b 3 1 1 log 3 log 3 b 2 2 log 3 2b dir. Bulduğumuz iki eşitliği de toplarsak; a log 2 log 3 ( 2b) 2 a log 2.3 2b 2 a log 6 2 2b a a 4b 1 2b 1 a 4b 2 2 2 2 a 4b 2 buluruz. 60
15 15 15 log 3 a olduğuna göre, log 75 5 log 3 ifadesinin değeri aşağıdakilerden hangisidir? A) a 2 a 2 2 B) C) 2a 1 2a 1 2 a a 1 a 1 D) E) 2 2 www.matematikkolay.net 15 15 15 15 15 15 15 15 15 15 15 log 75 log 15 log 5 1 log 5 5 log 5 log 3 log 5 a log 3 15 log 5 log log 15 : log 3 Çözüm 15 15 15 3 1 a 1 log 5 1 1 a 2 a a 2 veya buluruz. log 5 a 1 a a 1 2a 2a 1 74
2 3 25 x log 5 y log 6 olduğuna göre, log 150 ‘nin x ve y cinsinden değeri aşağıdakilerd 2 en hangisidir? x xy x y 2xy A) B) x y 1 xy 1 2xy 2x y xy 2x 2 C) D) 2xy 2x xy x xy 2x y E) 2xy 2x 3 3 3 3 3 2 y log 6 y log 3 log 2 y 1 log 2 y 1 log 2 tir. log 5 x idi. Bu ikisinin çarpımı; x.(y 1) : Çözüm log 2 5log3 2 3 25 25 25 5 5 5 2 3 log 5 tir. 1 log 150 log 25 log 6 1 log 6 2 1 1 1 1 1 log 2 log 3 1 2 2 2log 5 2log 5 1 1 2xy 2x y 1 1 1 2x 2x.(y 1) 2xy 2x 2xy 2x y buluruz. 2xy 2x www.matematikkolay.net 109
3 5 log15 ifadesin log 5 a ve l in a ve b cinsin og 6 b den değer old i n uğ ed una gö ir? a b A) a e, r a 1 B) b ab a 1 a b 1 ab a C) D) a 1 a b 1 a 1 E) ab a 1 3 5 3 log 5 a , log 6 l : b og 5 Çözüm 5 . log 3 3 3 3 1 3 3 3 3 3 3 3 3 3 6 a.b log 6 a.b log 3.2 a.b log 3 log 2 a.b log 2 a.b 1 dir. log 15 log 3.5 log 3 log 5 log15 log 10 log 2.5 log 2 log 5 1 a a 1 buluruz. a.b 1 a ab a 1 www.matematikkolay.net 123

