Soru Sor sayfası kullanılarak Logaritma konusu altında Logaritmik Denklemler, Logaritma Denklem Çözme, Logaritma Kök Bulma ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
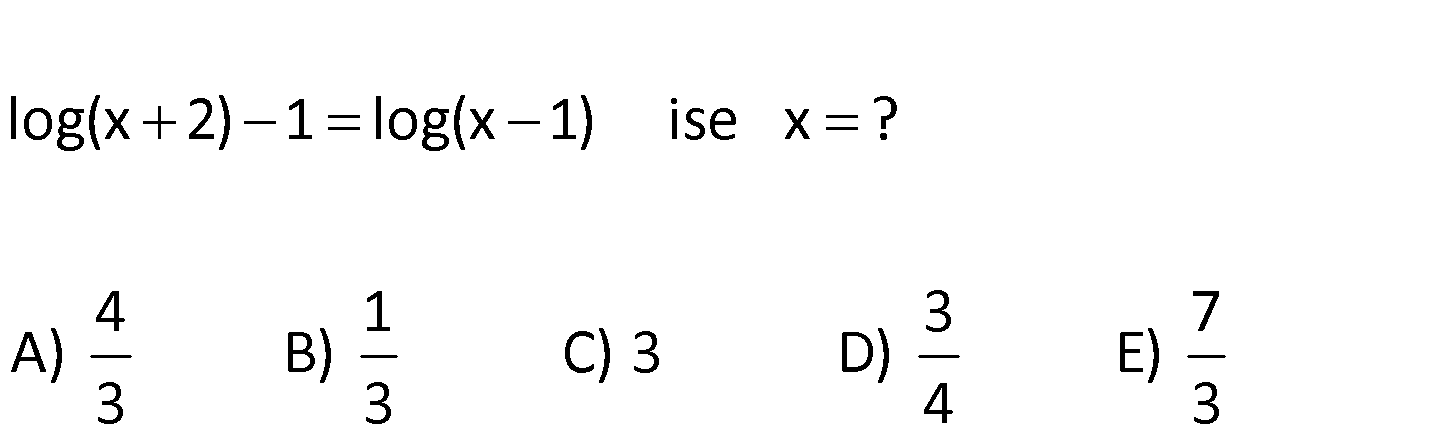
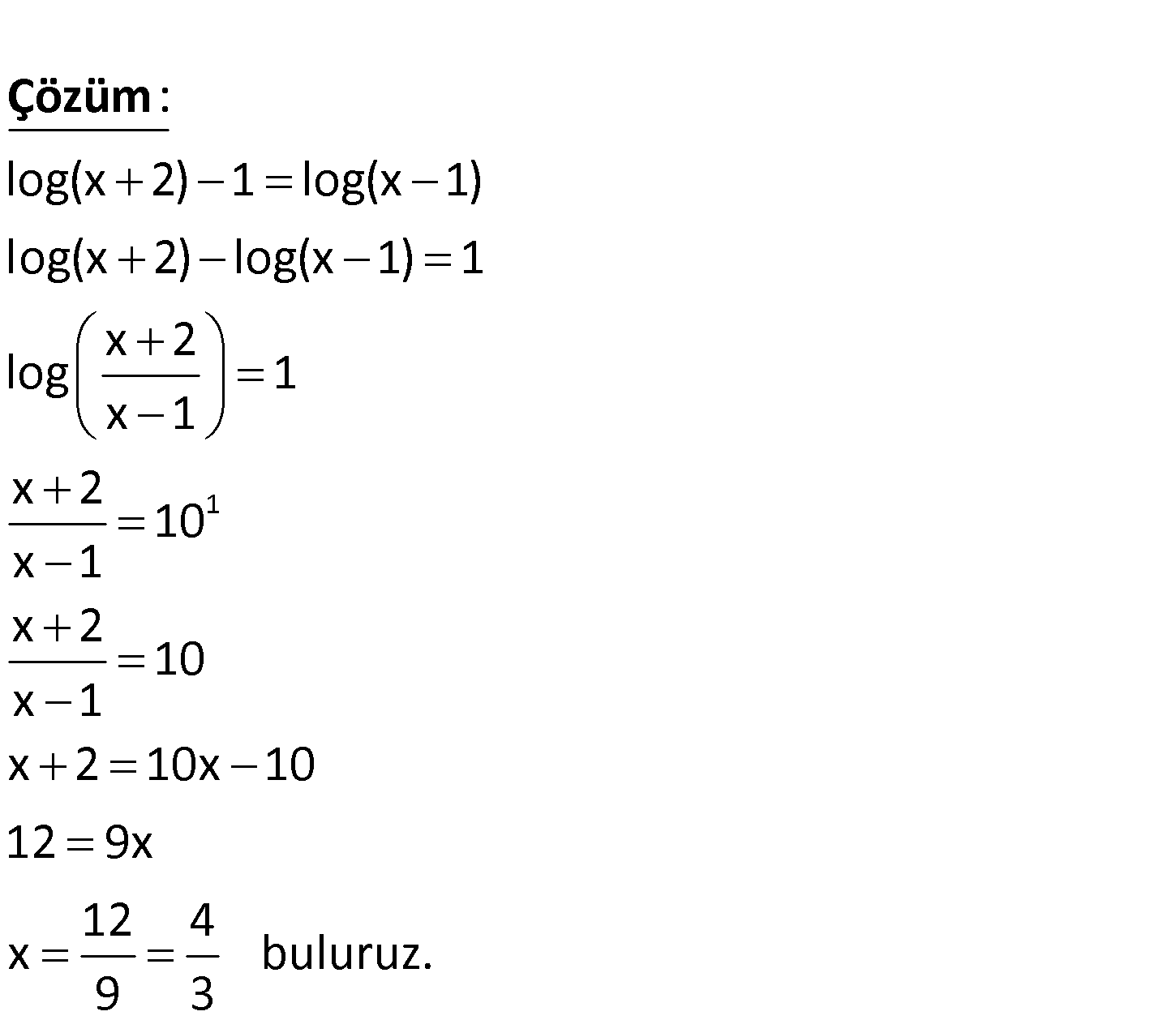
2.SORU

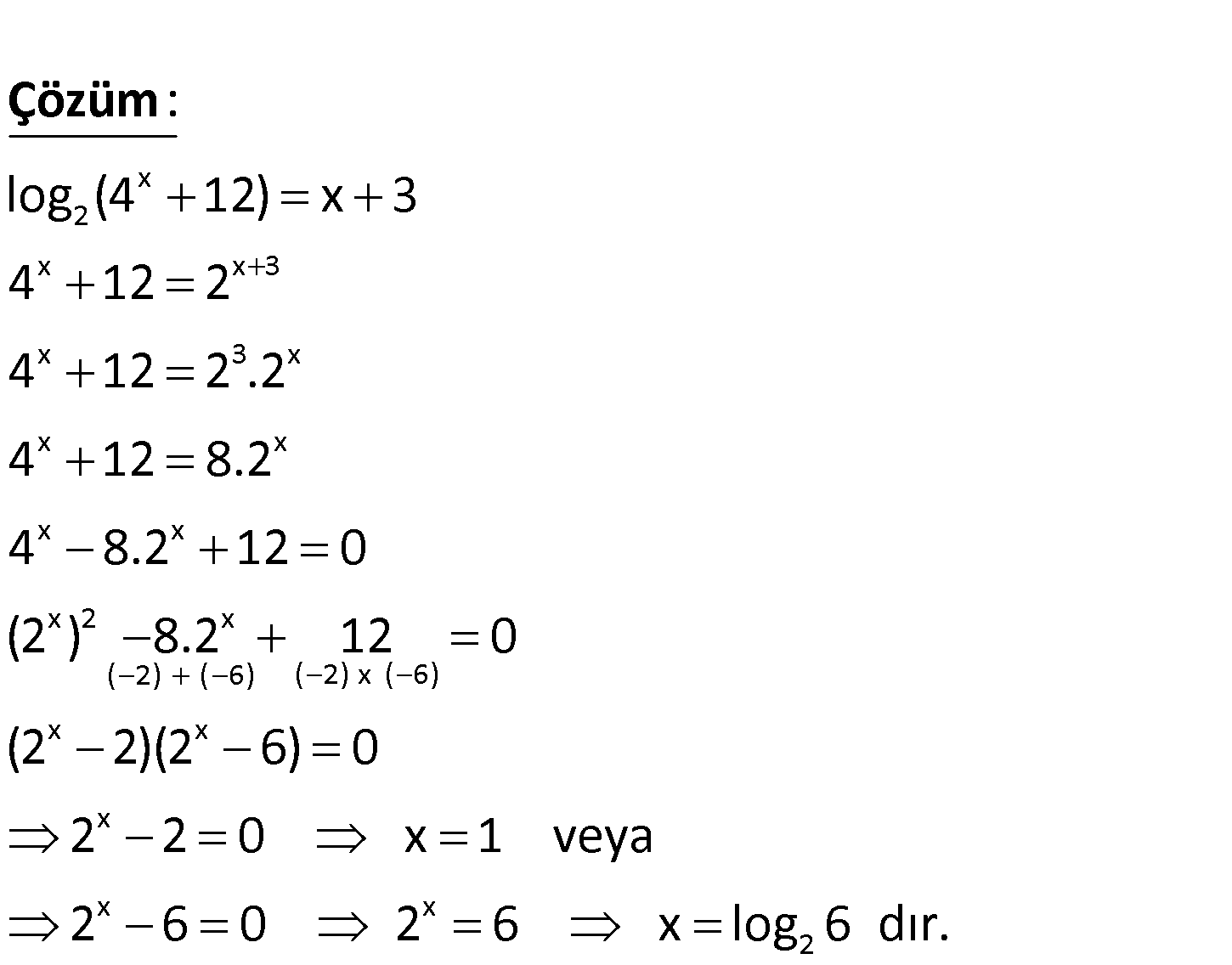
3.SORU
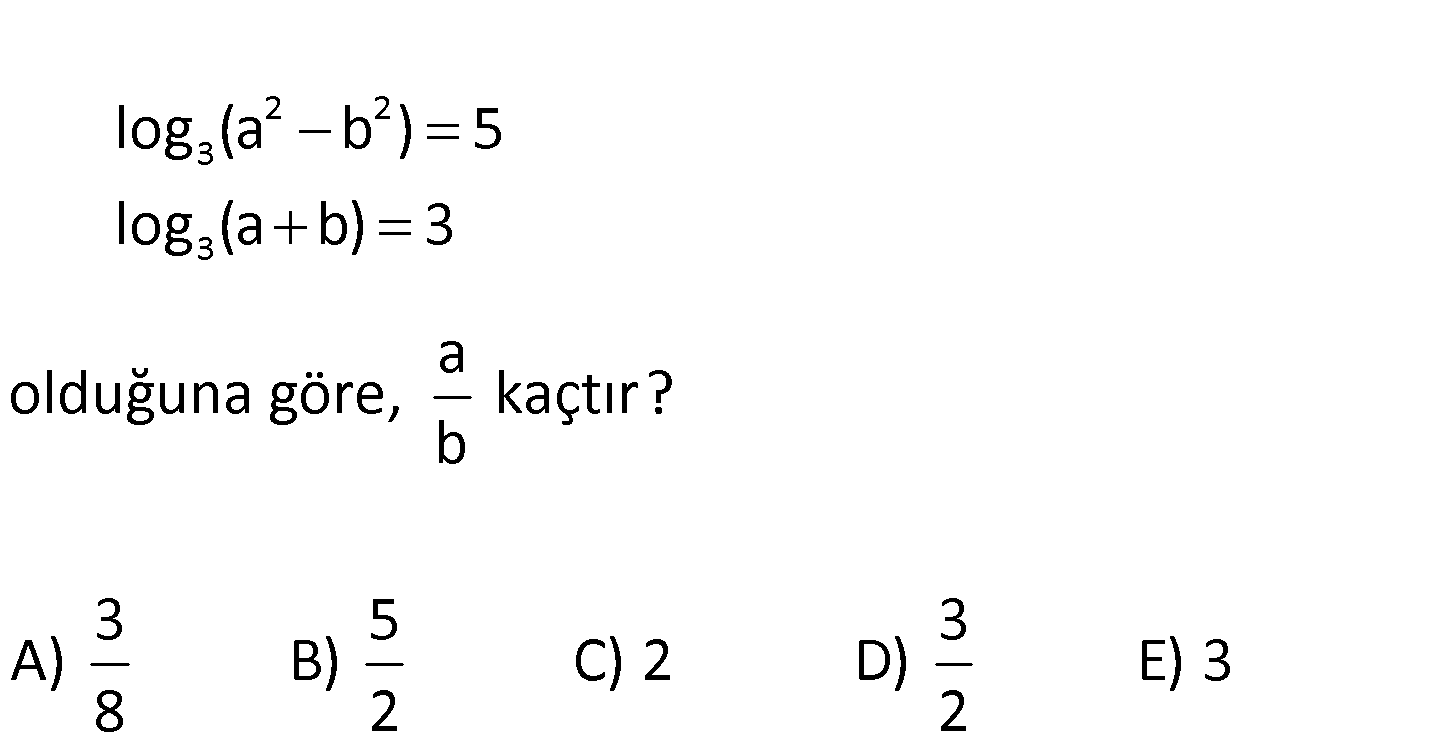

4.SORU
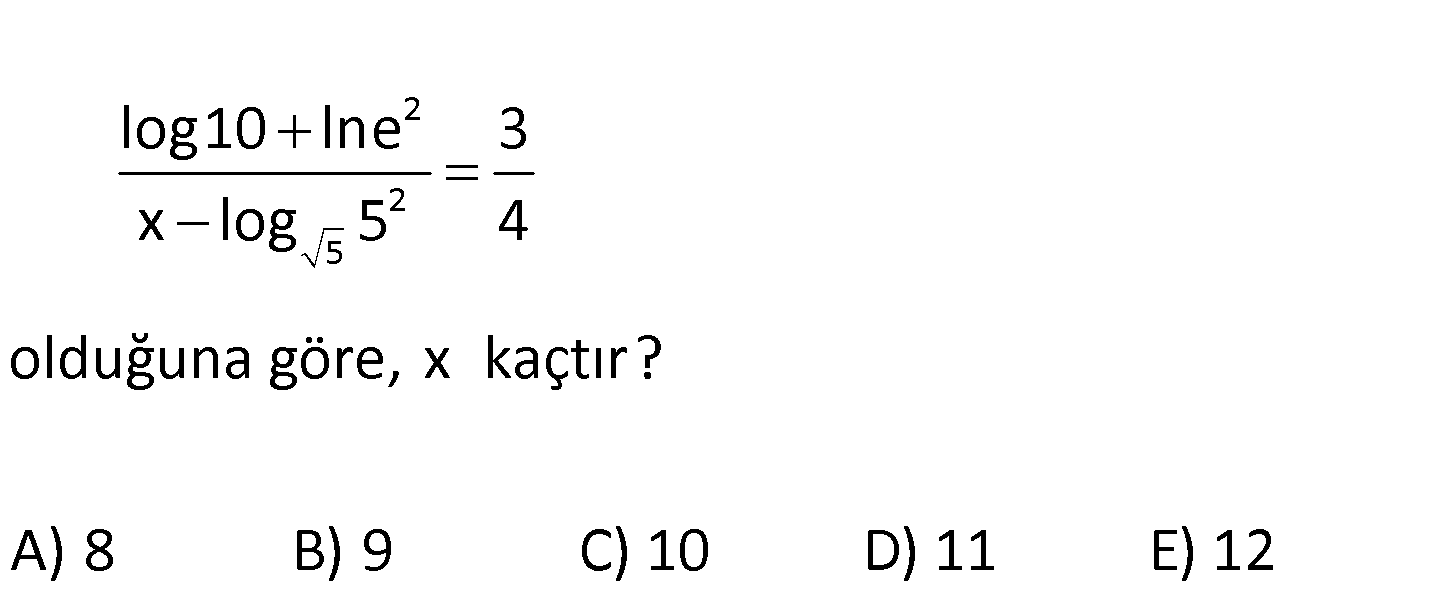
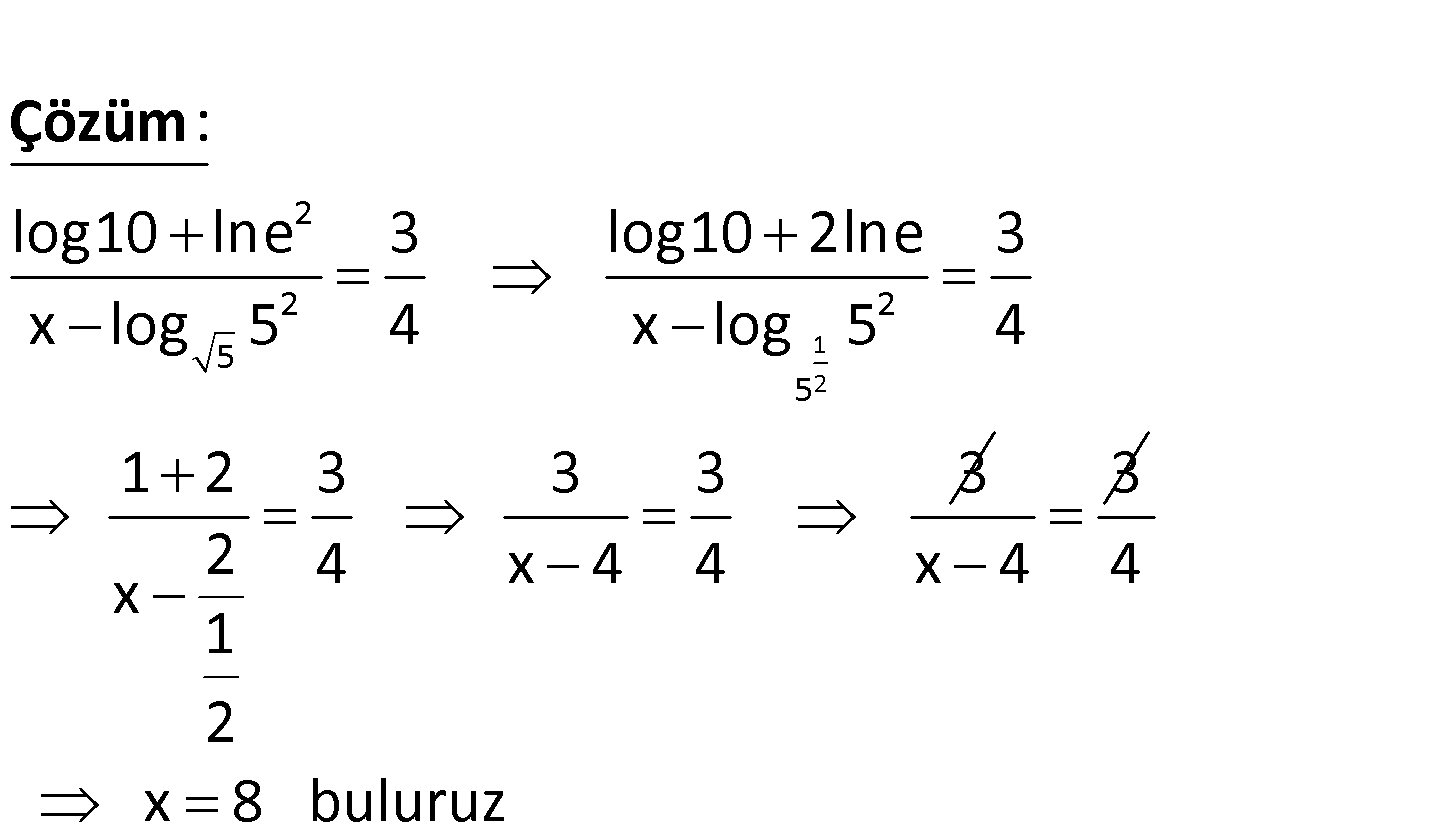
5.SORU

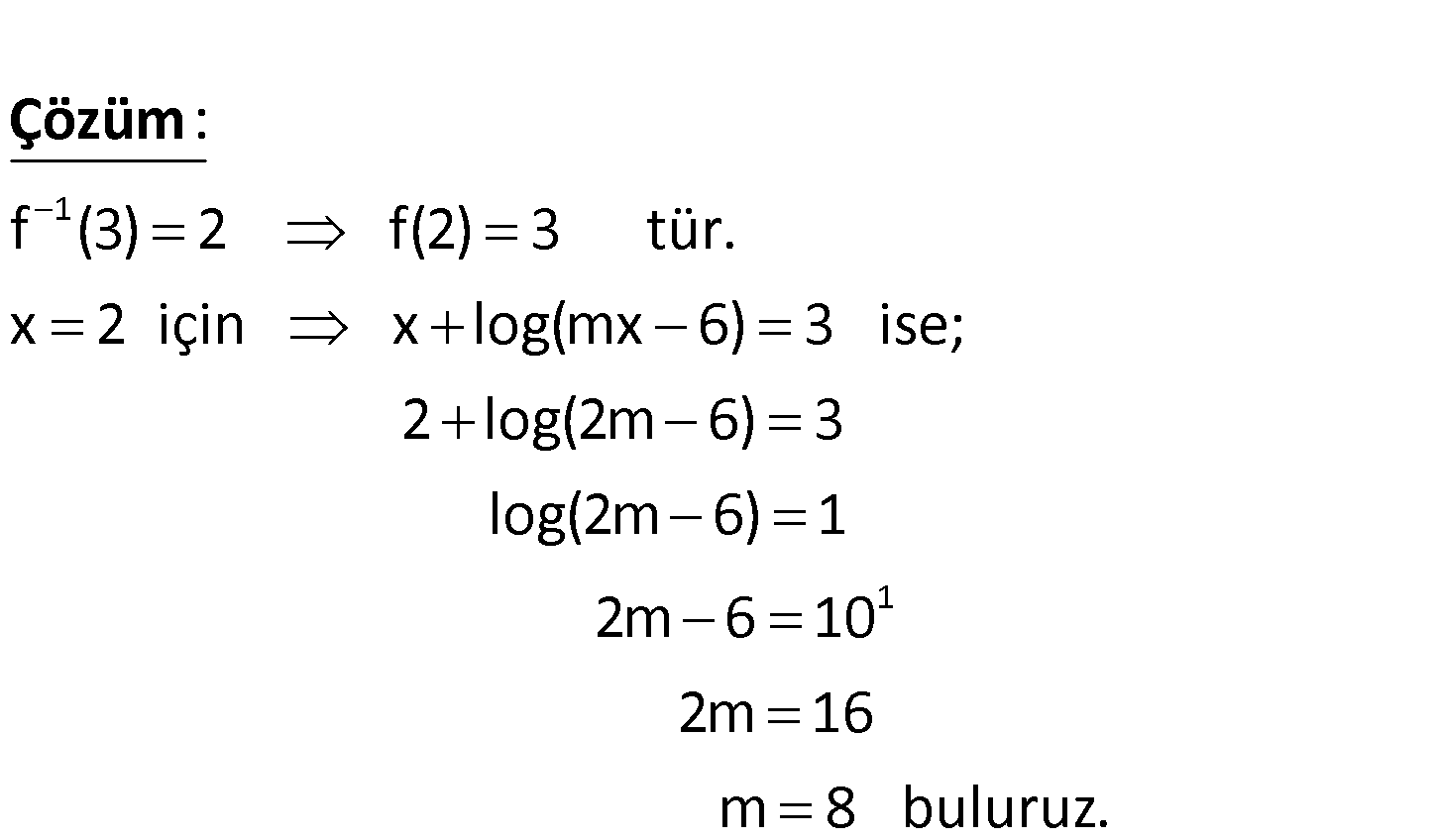
6.SORU
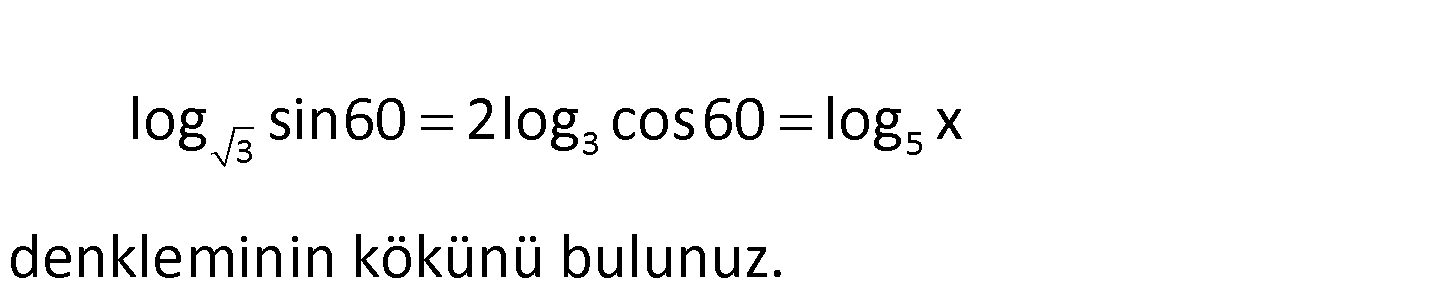

7.SORU


8.SORU
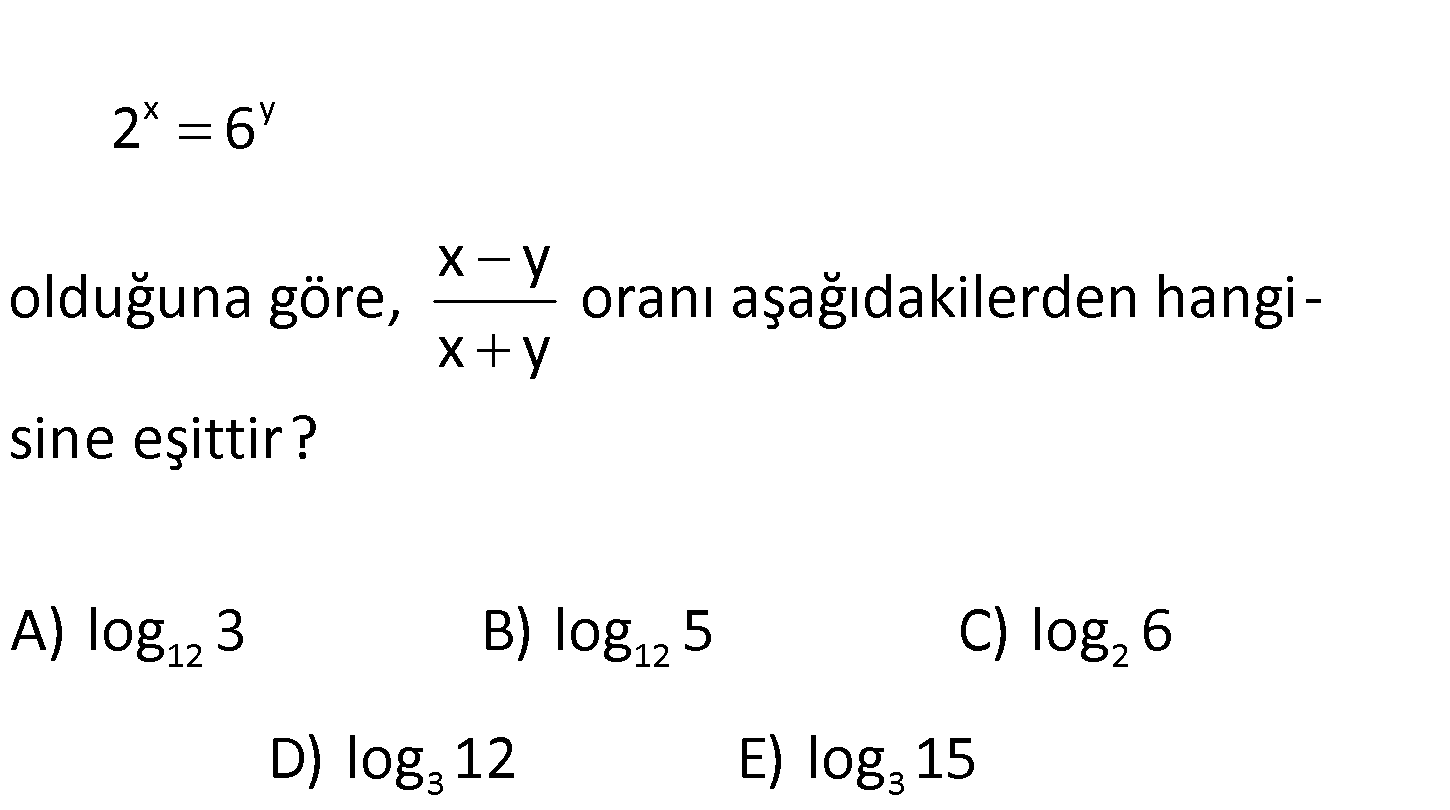
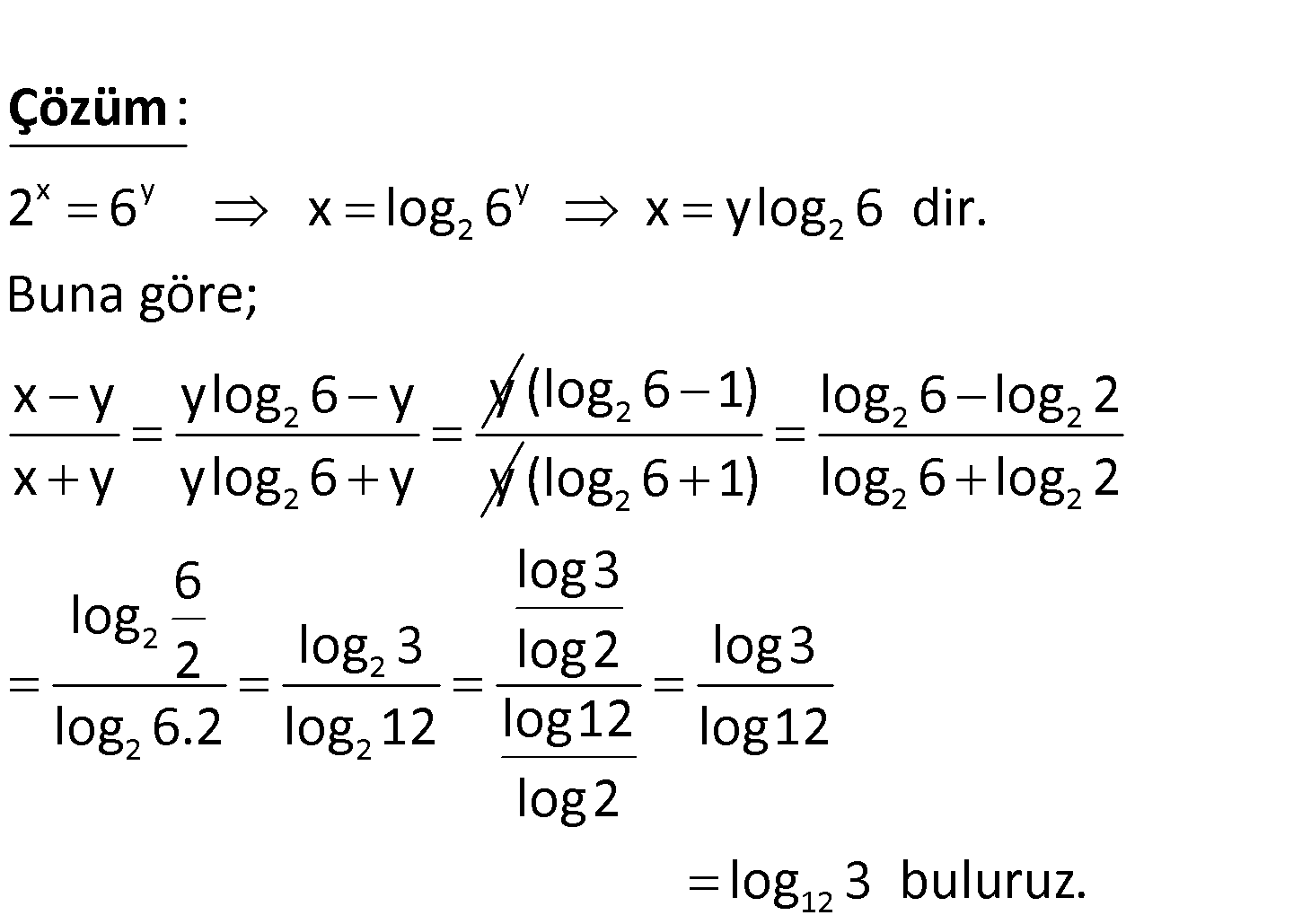
9.SORU
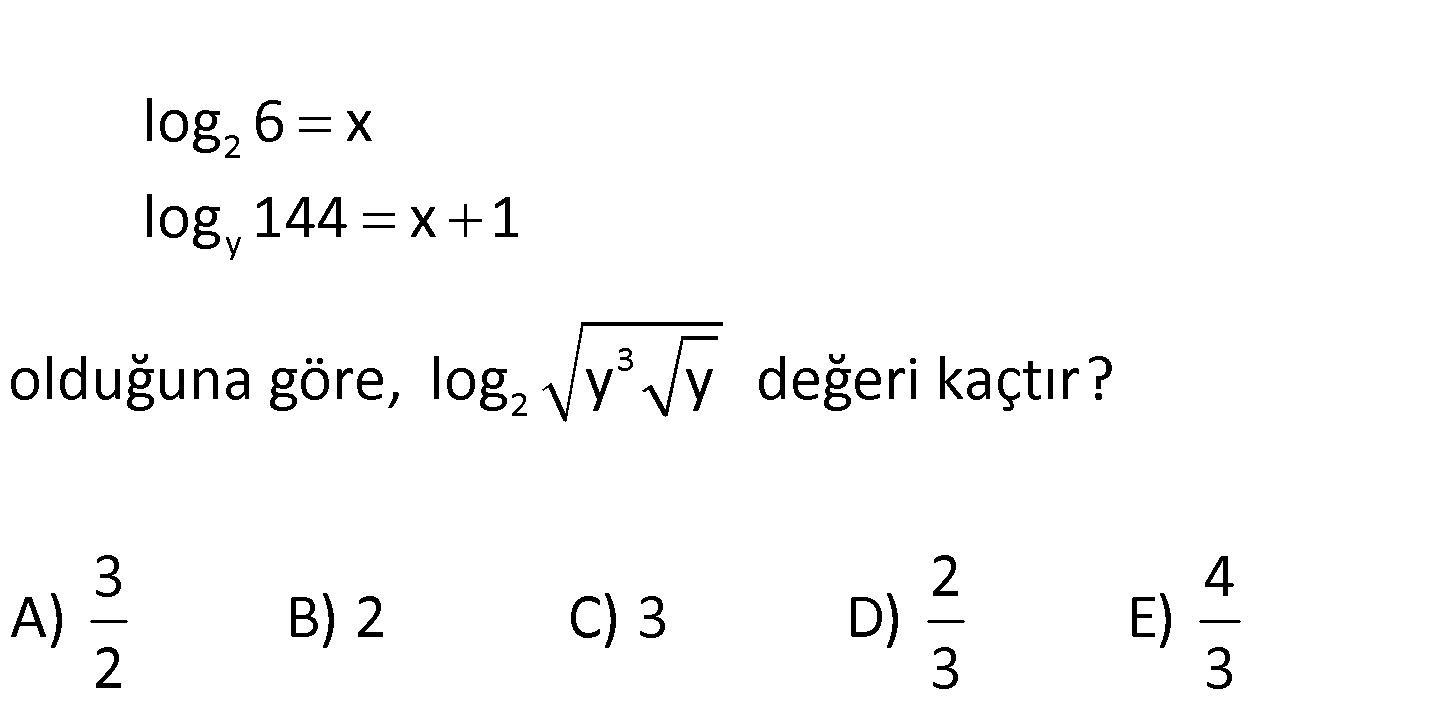

10.SORU

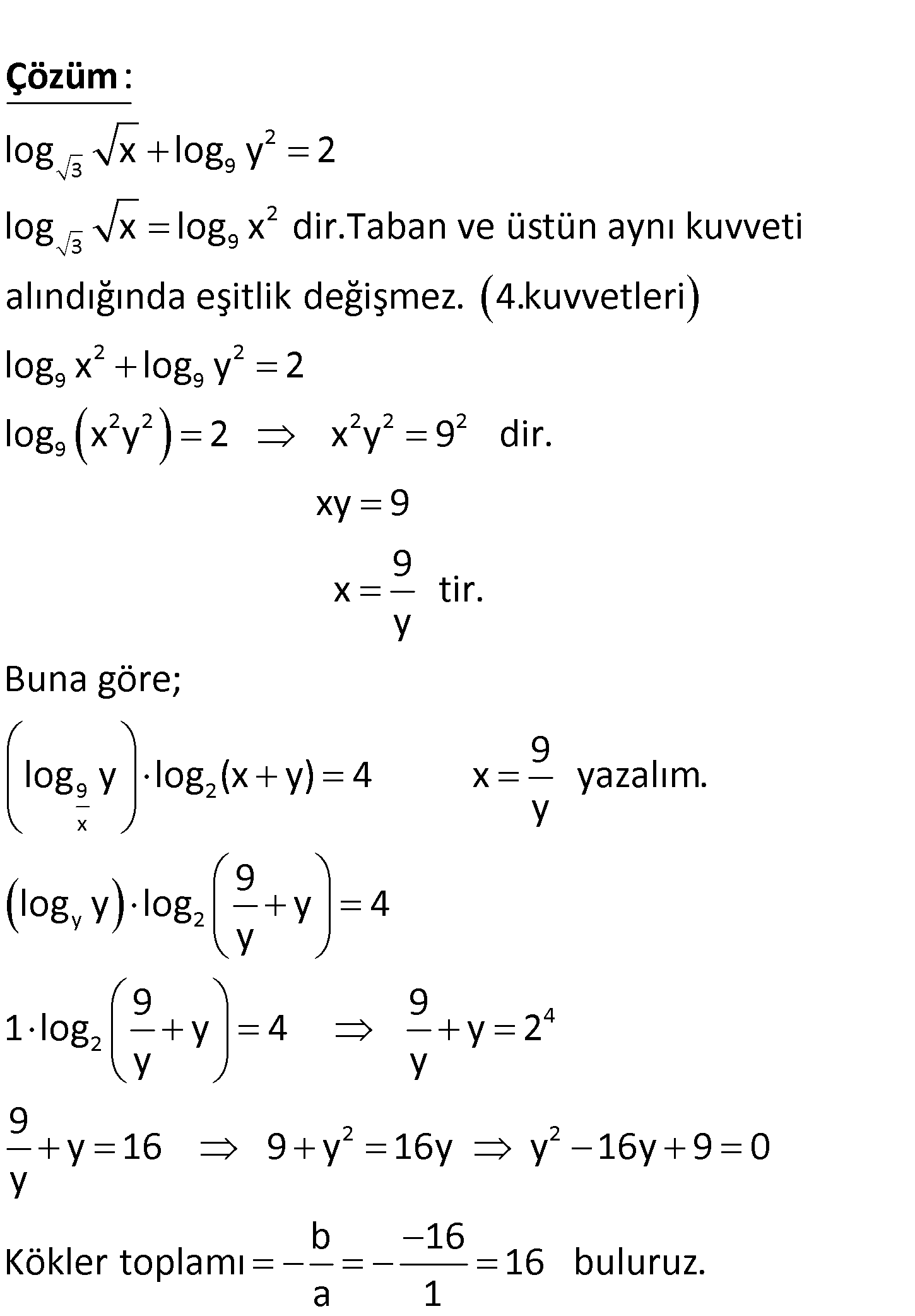
11.SORU
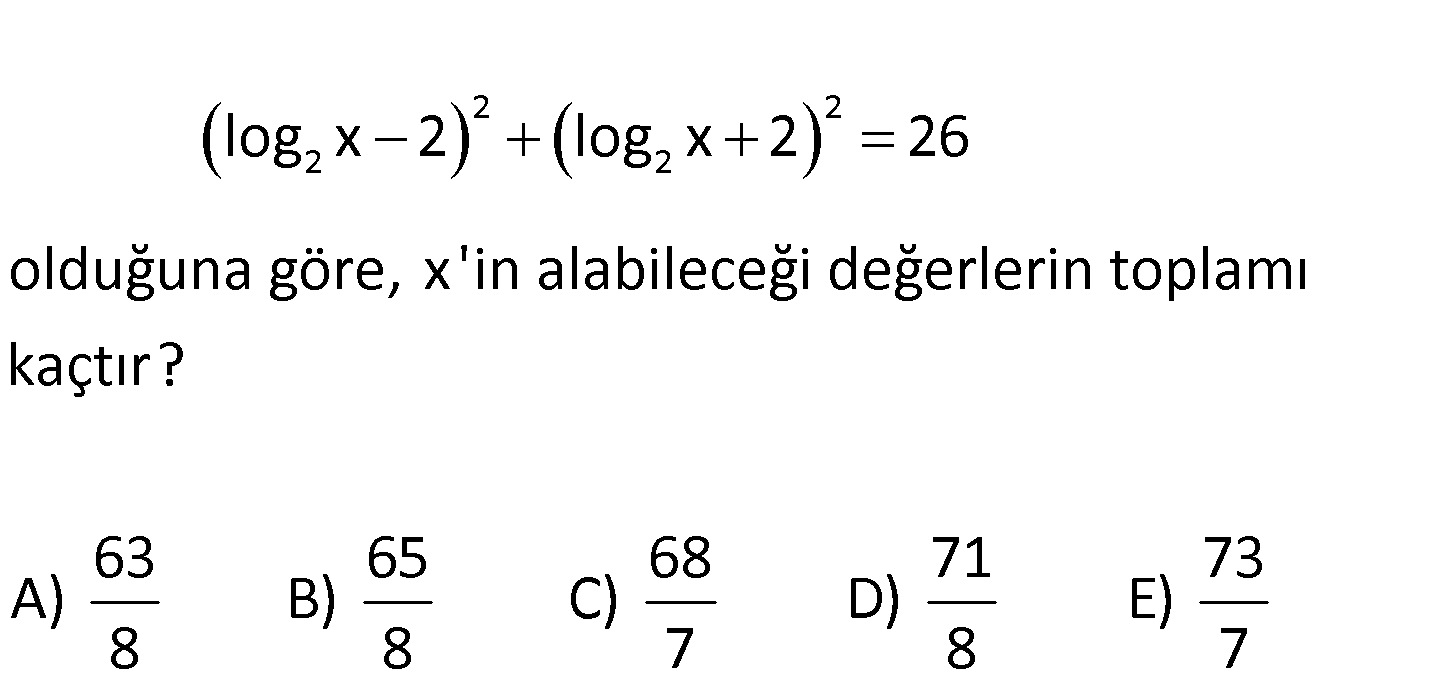

Diğer Soru Tipleri için Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
log(x 2) 1 log(x 1) ise x ? 4 1 3 7 A) B) C) 3 D) E) 3 3 4 3 1 log(x 2) 1 log(x 1) log(x 2) log(x 1) 1 x 2 log 1 x 1 x 2 10 x 1 x 2 10 x 1 x 2 10x 10 12 9x 1 : x Çözüm 2 4 buluruz. 9 3 2
www.matematikkolay.net x 2 log (4 12) x 3 olduğuna göre, denkleminin köklerinden biri aşağı – dakilerden hangisidir? A) lo 3 2 2 2 g 6 B) log 3 C) 2 D) log 9 E) log 6 x 2 x x 3 x 3 x x x x x x 2 x ( 2) ( 6) ( 2) x ( 6 log (4 12) x 3 4 12 2 4 12 2 .2 4 12 8.2 4 8.2 12 0 ( : 2 ) 8.2 12 Çözüm ) x x x x x 2 0 (2 2)(2 6) 0 2 2 0 x 1 veya 2 6 0 2 6 x log 6 dır. 9
2 2 3 3 log (a b ) 5 log (a b) 3 a olduğuna göre, kaçtır? b 3 5 3 A) B) C) 2 D) E) 3 8 2 2 www.matematikkolay.net 3 3 3 2 2 3 3 5 2 3 log (a b) 3 a b 3 27 dir. log (a b ) 5 log (a b)(a b) 5 (a b)(a b) 3 a b 3 9 dur. : Çözüm a b 27 a b 9 2a 36 a 18 a b 27 18 b 27 b 9 dur. Buna göre; a 18 2 buluruz. b 9 37
www.matematikkolay.net 2 2 5 log10 lne 3 x log 5 4 olduğuna göre, x kaçtır? A) 8 B) 9 C) 10 D) 11 E) 12 1 2 2 2 2 5 5 log10 lne 3 log10 2lne 3 x log 5 4 x log 5 4 1 2 3 3 3 3 2 4 x 4 4 : x 1 2 Çözüm 3 x 4 4 x 8 buluruz 40
www.matematikkolay.net 1 Tanımlı olduğu aralıkta f(x) x log(mx 6) f (3) 2 olduğuna göre, m kaçtır? A) 4 B) 6 C) 8 D) 10 E) 12 1 f (3) 2 f(2) 3 tür. x 2 için x log(mx 6) 3 ise; : Çözüm 1 2 log(2m 6) 3 log(2m 6) 1 2m 6 10 2m 16 m 8 buluruz. 43
3 3 5 log sin60 2log cos60 log x denkleminin kökünü bulunuz. www.matematikkolay.net 31/2 3 5 3 3 5 3 3 5 3 log sin60 2log cos60 log x 1 log sin60 2log cos60 log x 1 2 2log sin60 2log cos60 log x 2(log s : Çözüm 3 5 3 3 5 3 5 3 5 3 5 1 2 3 5 in60 log cos60) log x 2(log sin60 log cos60) log x sin60 2.log log x cos60 2.log tan60 log x 2.log 3 log x 2.log 3 log x 2 1 2 3 5 5 log 3 log x 1 log x x 5 buluruz. 61
www.matematikkolay.net 2 3 (log x) 2 7 olduğuna göre, x ‘in alabileceği değerler çarpımı nedir? 2 2 3 3 3 3 3 3 3 3 log x 2 7 log x log x 3 log x 3 tür. log x 3 x 3 27 dir. log x 3 x 3 : Çözüm 1 dir. 27 1 27 1 bulunur. 27 63
x y 12 12 2 6 x y olduğuna göre, oranı aşağıdakilerden hangi – x y sine eşittir? A) log 3 B) log 5 C) lo 2 3 3 g 6 D) log 12 E) log 15 x y y 2 2 2 2 2 6 x log 6 x ylog 6 dir. Buna göre; x y ylog 6 y y x y ylog 6 y : Çözüm 2 (log 6 1) y 2 2 2 2 2 2 2 2 2 12 log 6 log 2 (log 6 1) log 6 log 2 6 log3 log 2 log 3 log2 log3 log 6.2 log 12 log12 log12 log2 log 3 buluruz. 104
2 y 3 2 log 6 x log 144 x 1 olduğuna göre, log y y değeri kaçtır? 3 2 4 A) B) 2 C) 3 D) E) 2 3 3 www.matematikkolay.net 2 y 2 y 2 2 y 2 log 6 değerine 1 eklersek log 144 elde ederiz. log 6 1 log 144 log 6 log 2 log 144 log 12 : Çözüm 01.Şub y 2 2 y 2 y 2 y 2 y 01.Şub 3 3 3 6 2 2 2 2 7 7 2 2 2 3 2 log 144 log 12 log 12 log 12 log 144 log 12 2log 12 log 12 log 12 y 2 y 2 y 4 tür. log y y log 4 4 log 4 2 log 2 2 7 log 2 log 2 buluruz. Şıklarda yok. 2 Herhalde soruda log y y değ 3 2 1 4 3 3 3 3 2 2 2 2 4 3 2 il de log y y değeri sorulmak istenmiş. Böyle olursa; log y y log 4 4 log 4.4 log 4 4 log 2 buluruz. 3 115
www.matematikkolay.net 2 3 9 9 2 x log x log y 2 log y log (x y) 4 olduğuna göre, y nin alabileceği bir birinden farklı değerlerin toplamı kaçtır? A) 6 B) 9 C) 12 D) 16 E) 20 2 3 9 2 3 9 log x log y 2 log x log x dir.Taban ve üstün aynı kuvveti alındığında eşitlik değiş : mez. 4.k Çözüm 2 2 9 9 2 2 2 2 2 9 9 2 x uvvetleri log x log y 2 log x y 2 x y 9 dir. xy 9 9 x tir. y Buna göre; 9 log y log (x y) 4 x yazalım. y l y 2 4 2 2 2 9 og y log y 4 y 9 9 1 log y 4 y 2 y y 9 y 16 9 y 16y y 16y 9 0 y b 16 Kökler toplamı 16 buluruz. a 1 134
2 2 2 2 log x 2 log x 2 26 olduğuna göre, x ‘in alabileceği değerlerin toplamı kaçtır? 63 A) B 8 65 68 71 73 ) C) D) E) 8 7 8 7 2 2 2 2 2 2 2 2 log x a olsun. a 2 a 2 26 olur. a 4a 4 a 4a 4 26 2a 8 26 2a 18 a 9 a 3 veya a 3 : t Çözüm 2 3 2 ür. log x 3 ise x 8 1 log x 3 ise x 2 dir. 8 Toplarsak ; 1 65 8 buluruz. 8 8 148

