Soru Sor sayfası kullanılarak İntegral ile Alan konusu altında y’ye göre integral ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
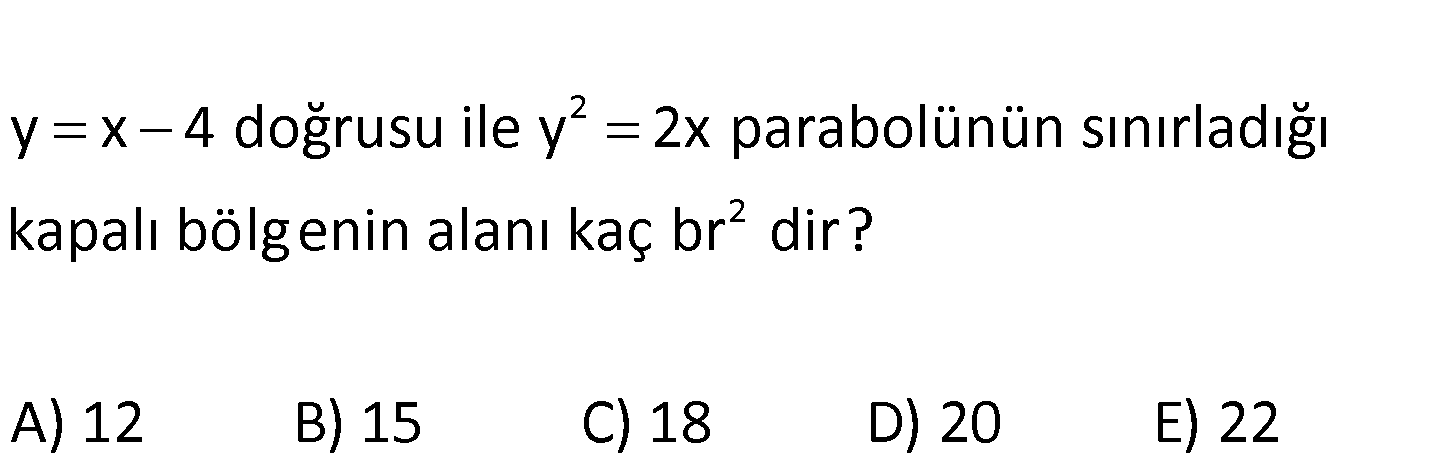
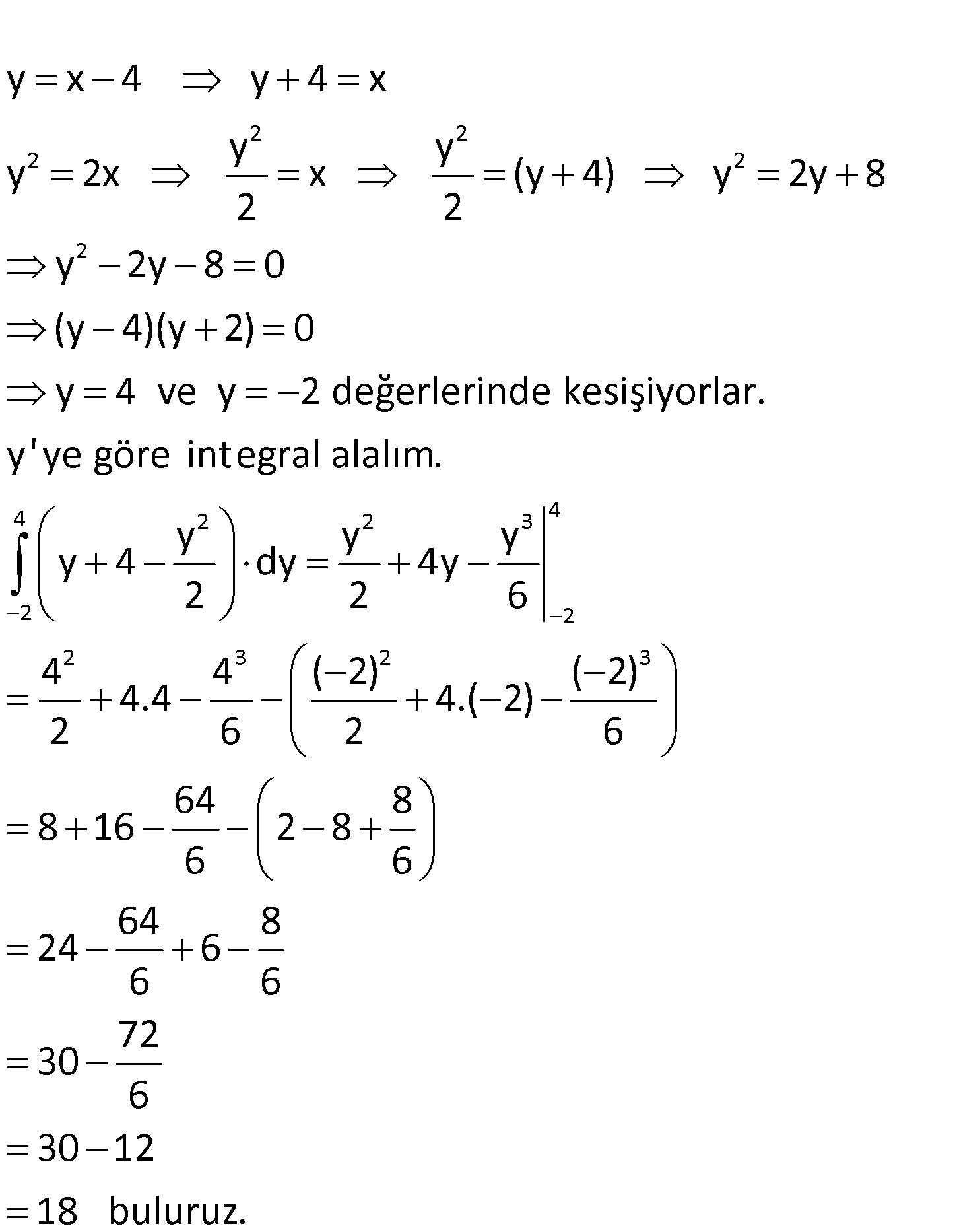
2.SORU
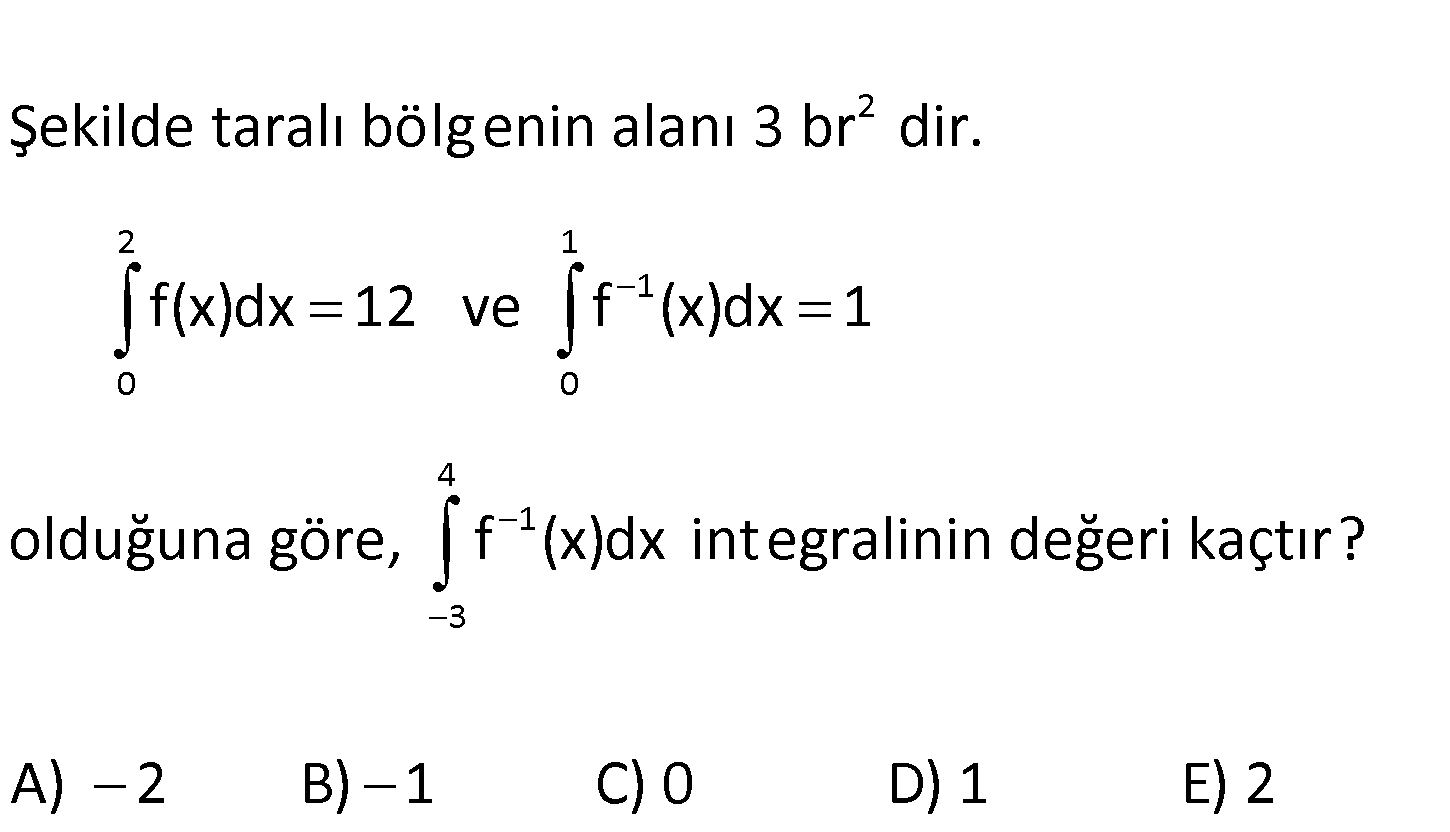

3.SORU


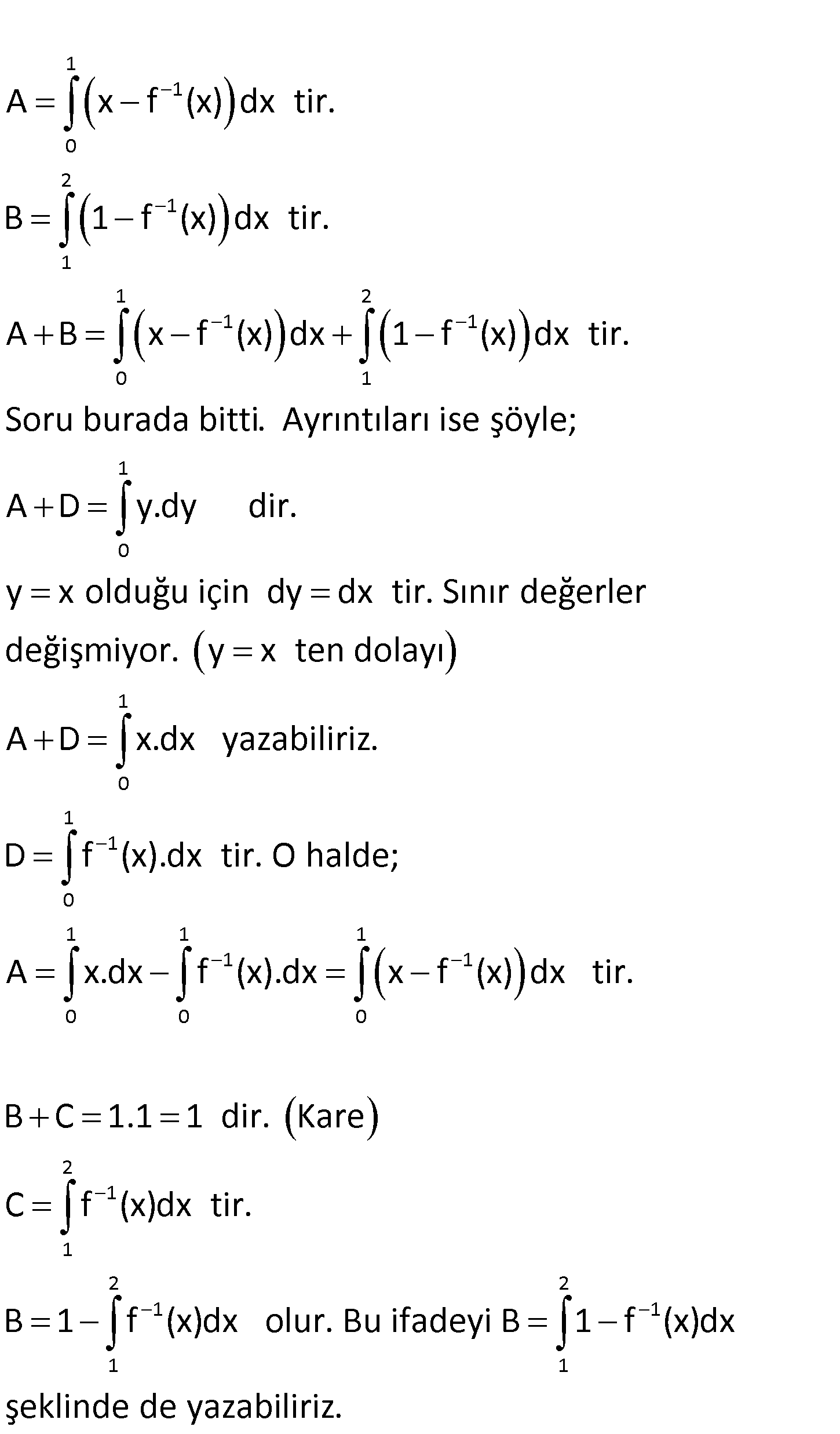
4.SORU
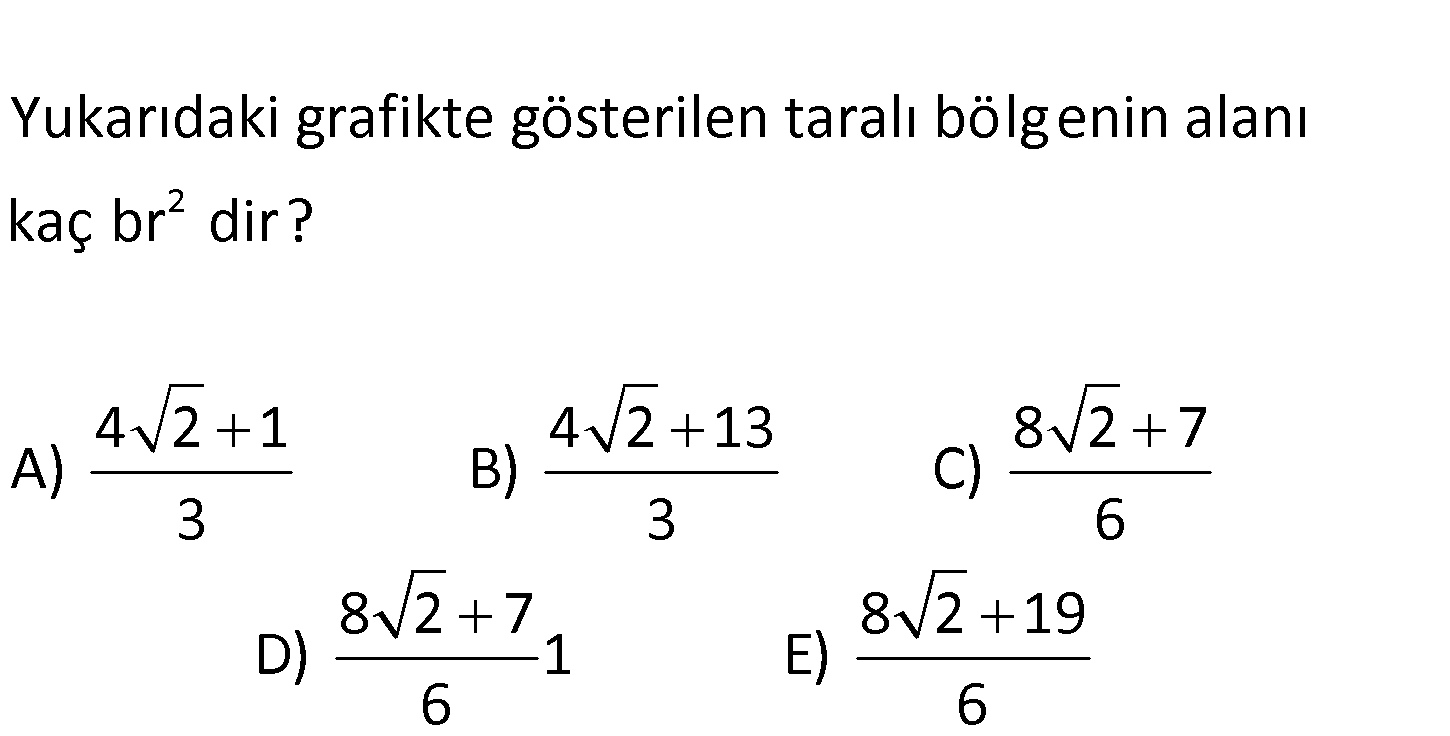

5.SORU
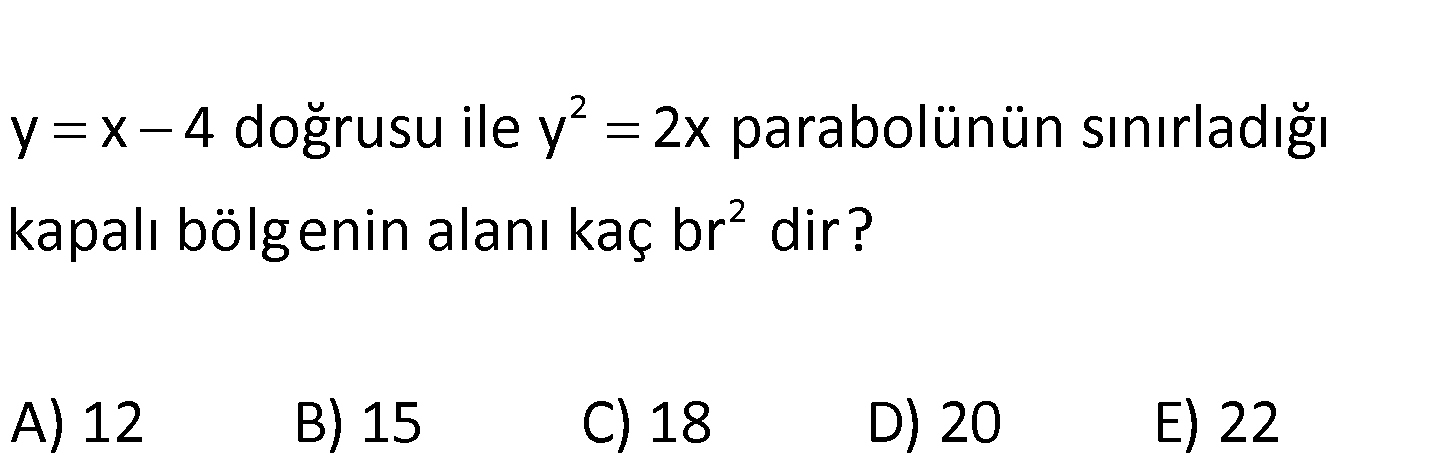
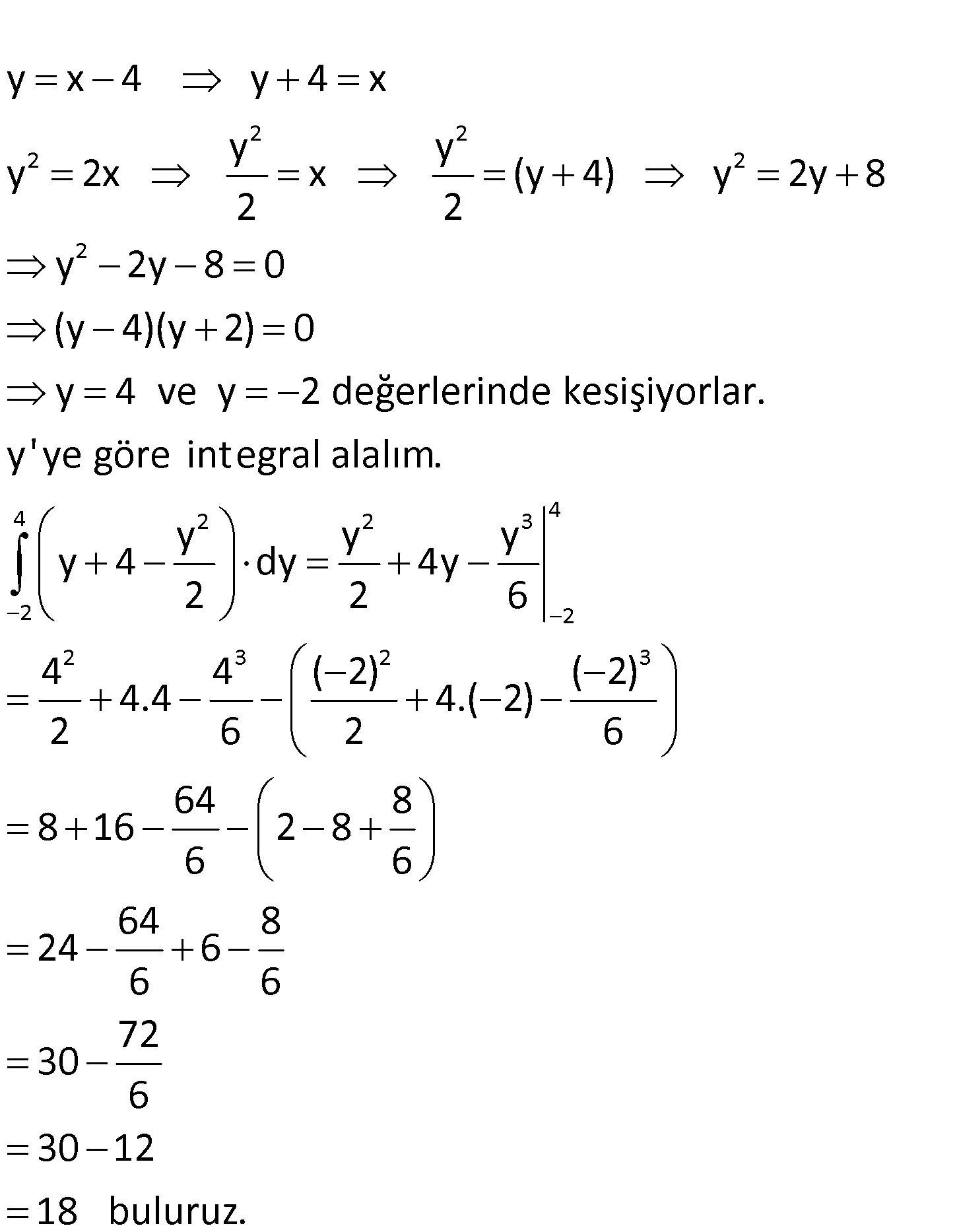
Diğer Soru Tipleri için Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
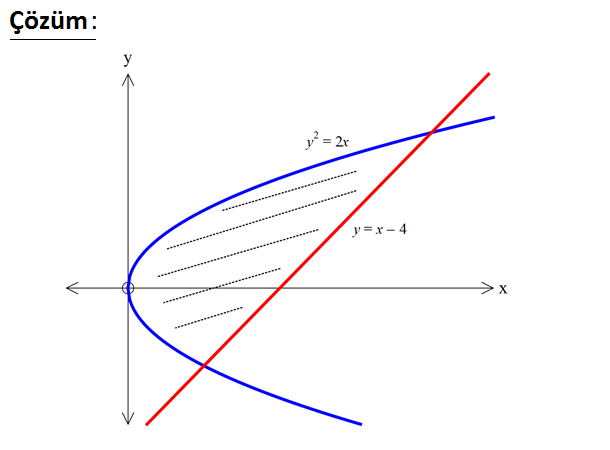
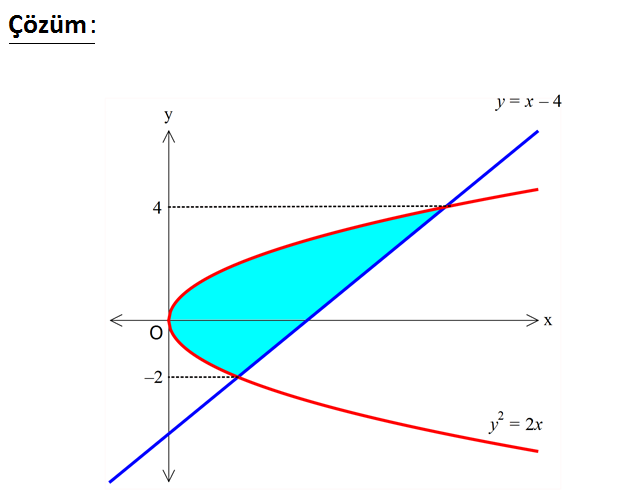
2 2 y x 4 doğrusu ile y 2x parabolünün sınırladığı kapalı bölg enin alanı kaç br dir? A) 12 B) 15 C) 18 D) 20 E) 22 www.matematikkolay.net 2 2 2 2 2 y x 4 y 4 x y y y 2x x (y 4) y 2y 8 2 2 y 2y 8 0 (y 4)(y 2) 0 y 4 ve y 2 değ 4 2 2 3 4 2 2 2 3 2 3 erlerinde kesişiyorlar. y’ye göre integral alalım. y y y y 4 dy 4y 2 2 6 4 4 ( 2) ( 2) 4.4 4.( 2) 2 6 2 6 64 8 8 16 2 8 6 6 64 8 24 6 6 6 72 30 6 30 12 18 buluruz. 7
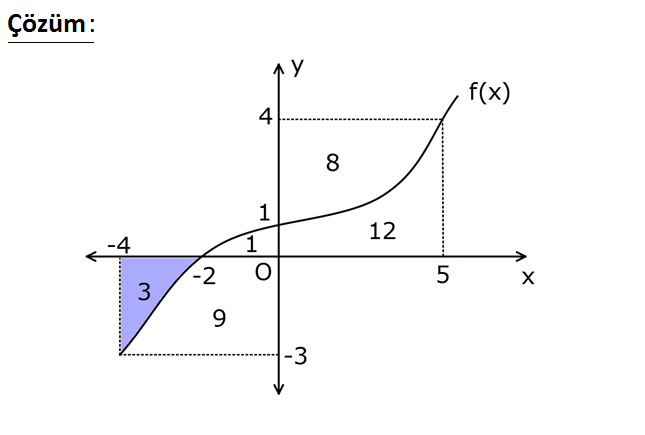
www.matematikkolay.net 2 2 1 1 0 0 Şekilde taralı bölg enin alanı 3 br dir. f(x)dx 12 ve f (x)dx 1 olduğuna göre, 4 1 3 f (x)dx integralinin değeri kaçtır? A) 2 B) 1 C) 0 D) 1 E) 2 4 1 3 Verilen integrallere göre alanların ölçüleri şekilde – ki gibidir. f (x)dx Eğri ile y ekseni ara 4 1 3 sındaki bölg eye bakılır. y ekseninin sağındaki alan , solundaki alan ( ) alınır. f (x)dx 8 1 9 2 buluruz. 31
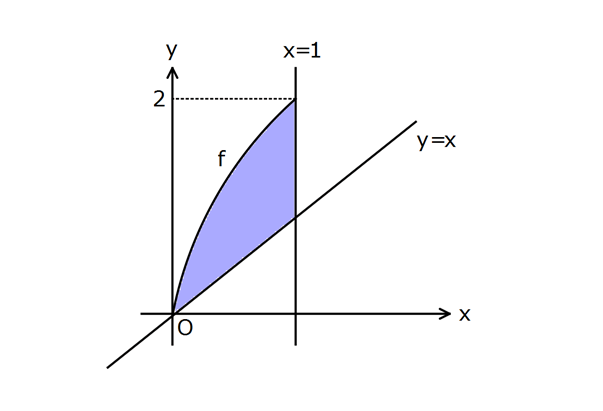
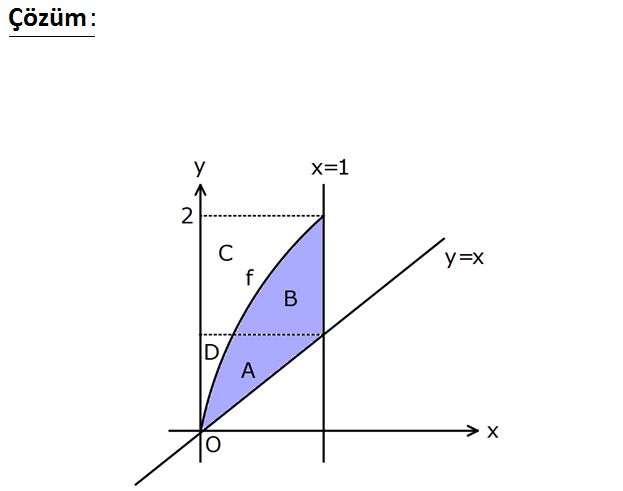
www.matematikkolay.net f fonksiyonu bire bir olmak üzere, birinci bölgede y x ve x 1 doğruları ile y f(x) eğrisi arasında kalan taralı bölg e aşağıda verilmiştir. 1 2 1 0 Taralı bölg enin alanının f (x) türünden ifadesi aşağıdakilerden hangisine eşittir? A) f (x)dx B) 2 1 0 1 1 0 1 2 1 1 0 1 1 2 1 1 0 1 2 f (x) dx C) x f (x) dx D) 2 f (x) dx f (x)dx E) x f (x) dx 1 f (x) dx LYS 2013 www.matematikkolay.net www.matematikkolay.net 1 1 0 2 1 1 1 2 1 1 0 1 A x f (x) dx tir. B 1 f (x) dx tir. A B x f (x) dx 1 f (x) dx tir. Soru burada bitti. 1 0 1 0 1 1 0 1 1 1 1 0 0 Ayrıntıları ise şöyle; A D y.dy dir. y x olduğu için dy dx tir. Sınır değerler değişmiyor. y x ten dolayı A D x.dx yazabiliriz. D f (x).dx tir. O halde; A x.dx f (x).dx x f (x) 1 0 2 1 1 2 2 1 1 1 1 dx tir. B C 1.1 1 dir. Kare C f (x)dx tir. B 1 f (x)dx olur. Bu ifadeyi B 1 f (x)dx şeklinde de yazabiliriz. www.matematikkolay.net 32
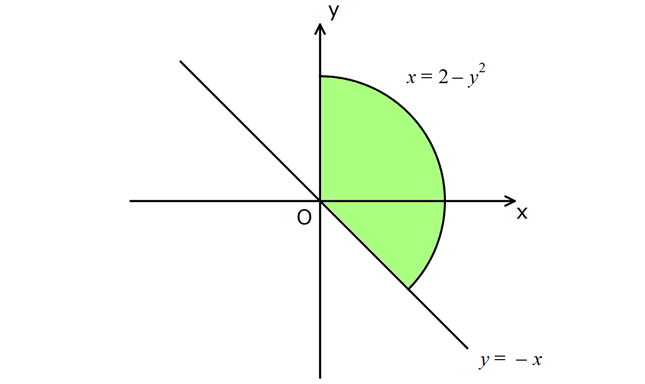
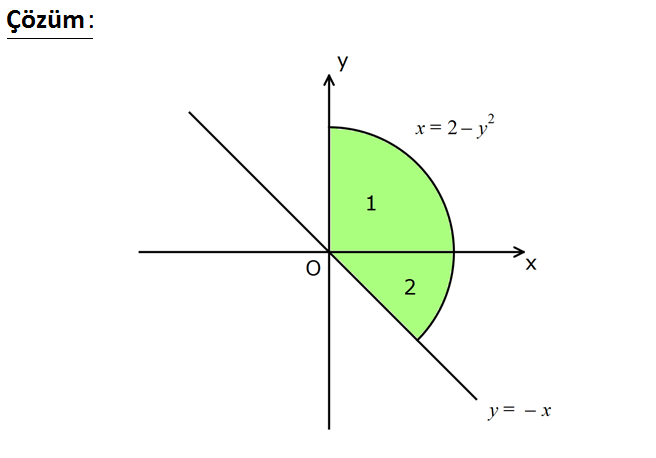
www.matematikkolay.net 2 Yukarıdaki grafikte gösterilen taralı bölgenin alanı kaç br dir? 4 2 1 4 2 13 8 2 7 A) B) C) 3 3 6 8 2 7 8 2 19 D) 1 E) 6 6 www.matematikkolay.net 2 y’ye göre integral alacağız. İki parçaya ayıralım. 1. parça x 2 y eğrisi ile x 0 arasındaki ala 2 3 2 2 0 0 2 ndır. x 0 için y 2 dir. O halde y sınır değerleri 2 ve 0 olacaktır. y 2 2 4 2 Alan 2 y dy 2y 2 2 3 3 3 2.parça x 2 y eğrisi ile x y arasındaki alandır. y 0 dan bunların kesiştiği yere kadar integral al 2 2 0 3 2 0 2 1 1 malıyız. Kesiştikleri yeri bulalım. 2 y y 0 y y 2 y 2 y 1 0 y 1 dir. y’nin negatif olduğu yerde keşisiyor y y Alan 2 y y dy 2y 3 2 1 1 1 1 7 0 2 2 dır. 3 2 3 2 6 Tüm alanlar topla 4 2 7 8 2 7 mı buluruz. 3 6 6 42
2 2 y x 4 doğrusu ile y 2x parabolünün sınırladığı kapalı bölg enin alanı kaç br dir? A) 12 B) 15 C) 18 D) 20 E) 22 www.matematikkolay.net 2 2 2 2 2 y x 4 y 4 x y y y 2x x (y 4) y 2y 8 2 2 y 2y 8 0 (y 4)(y 2) 0 y 4 ve y 2 değ 4 2 2 3 4 2 2 2 3 2 3 erlerinde kesişiyorlar. y’ye göre integral alalım. y y y y 4 dy 4y 2 2 6 4 4 ( 2) ( 2) 4.4 4.( 2) 2 6 2 6 64 8 8 16 2 8 6 6 64 8 24 6 6 6 72 30 6 30 12 18 buluruz. 55

