Soru Sor sayfası kullanılarak İntegral ile Alan konusu altında x ekseninin altında kalan, x eksenine göre integralin değeri ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
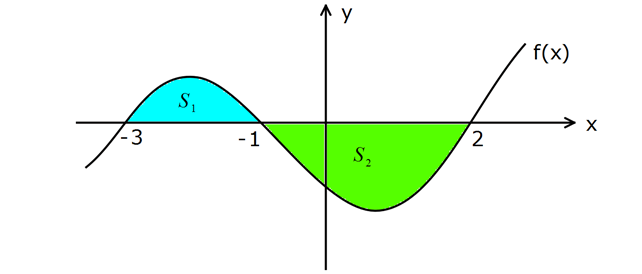
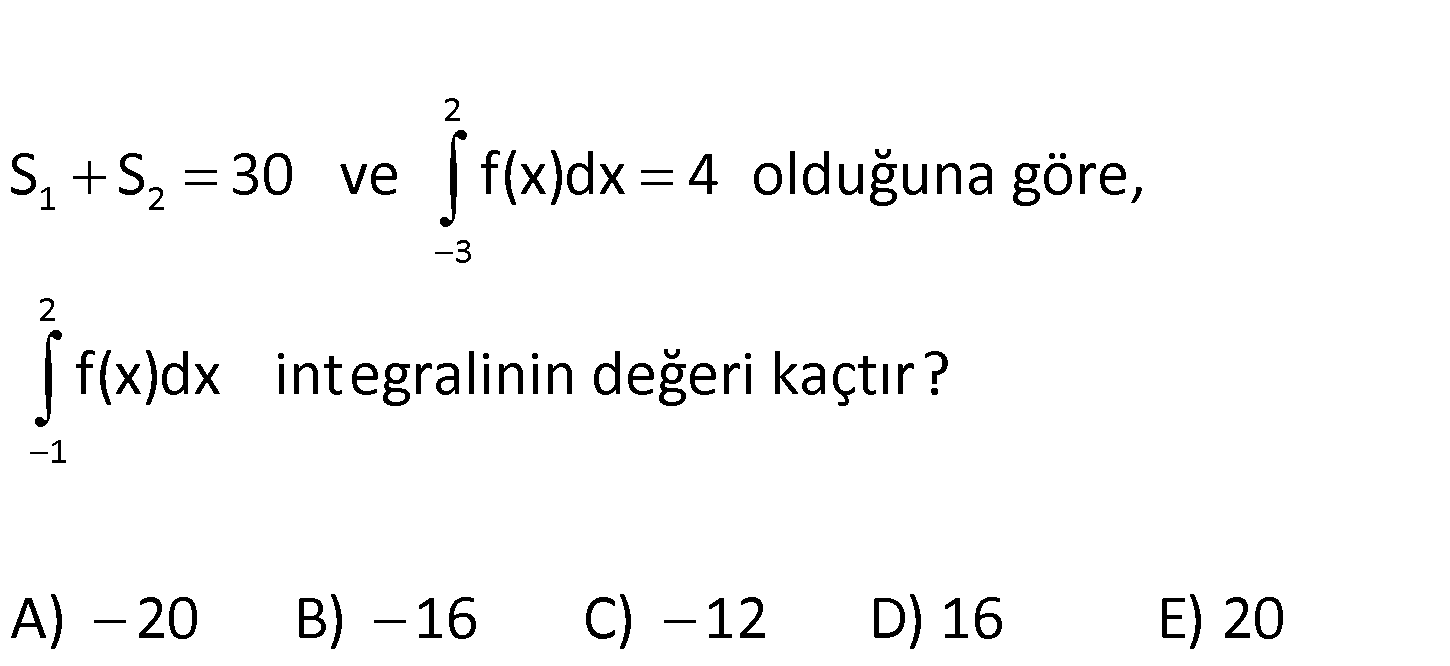

2.SORU
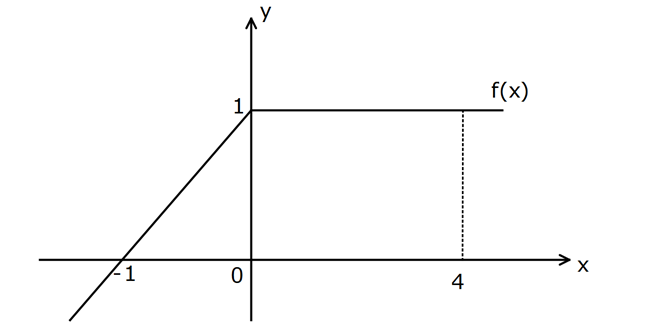

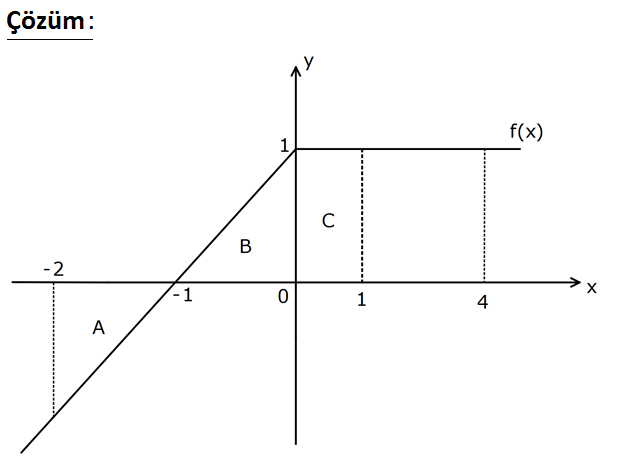
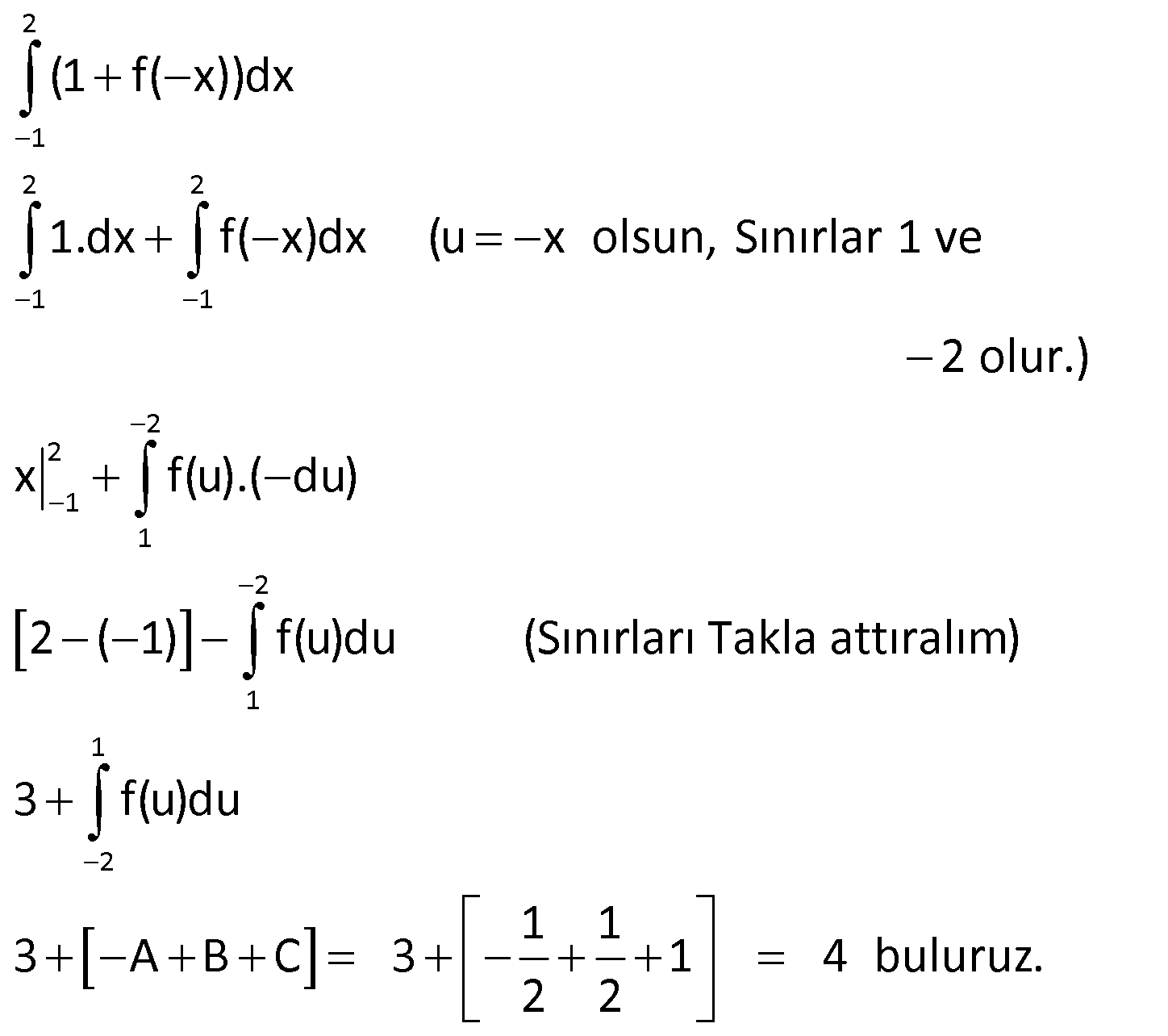
3.SORU
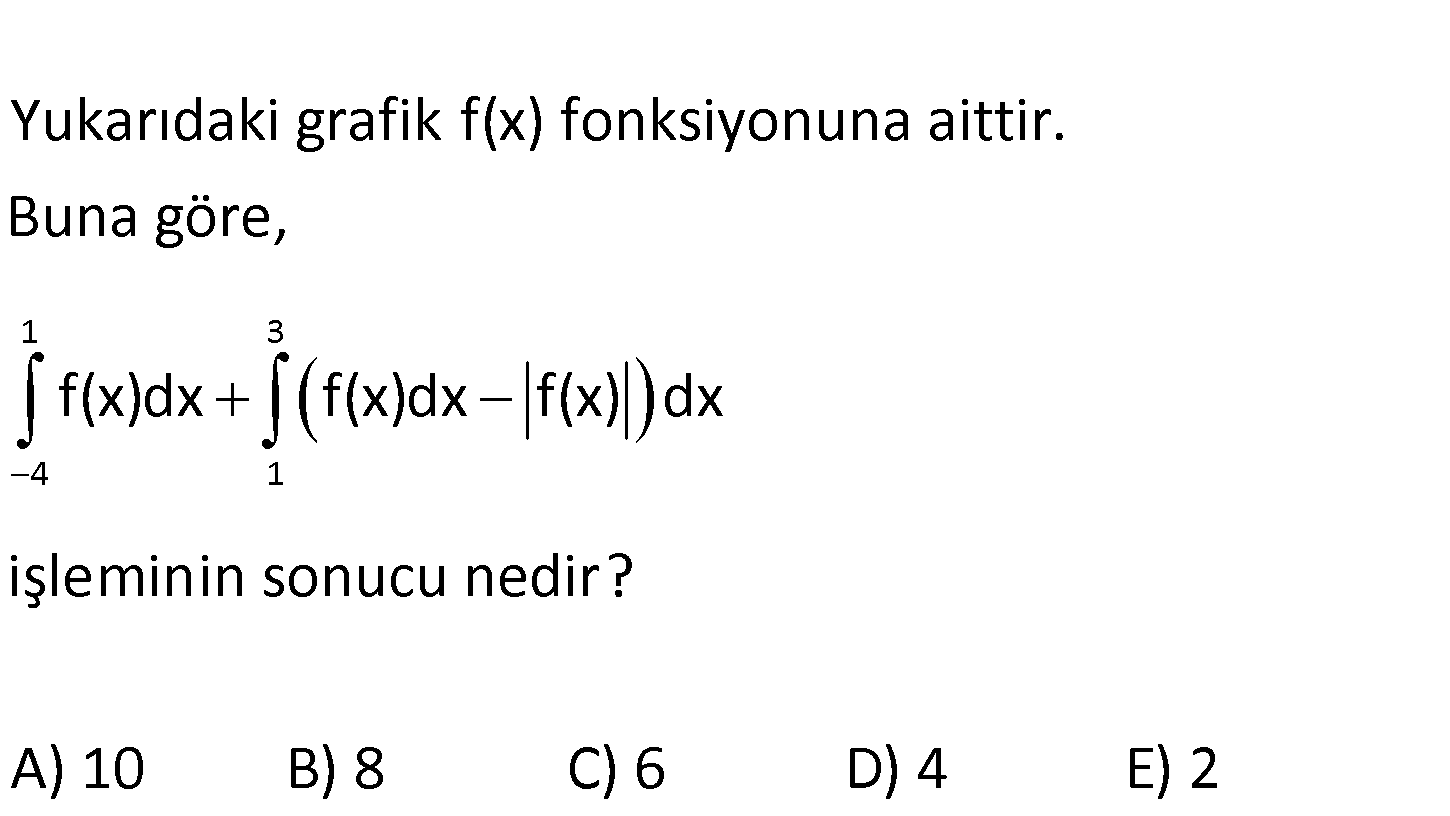

4.SORU
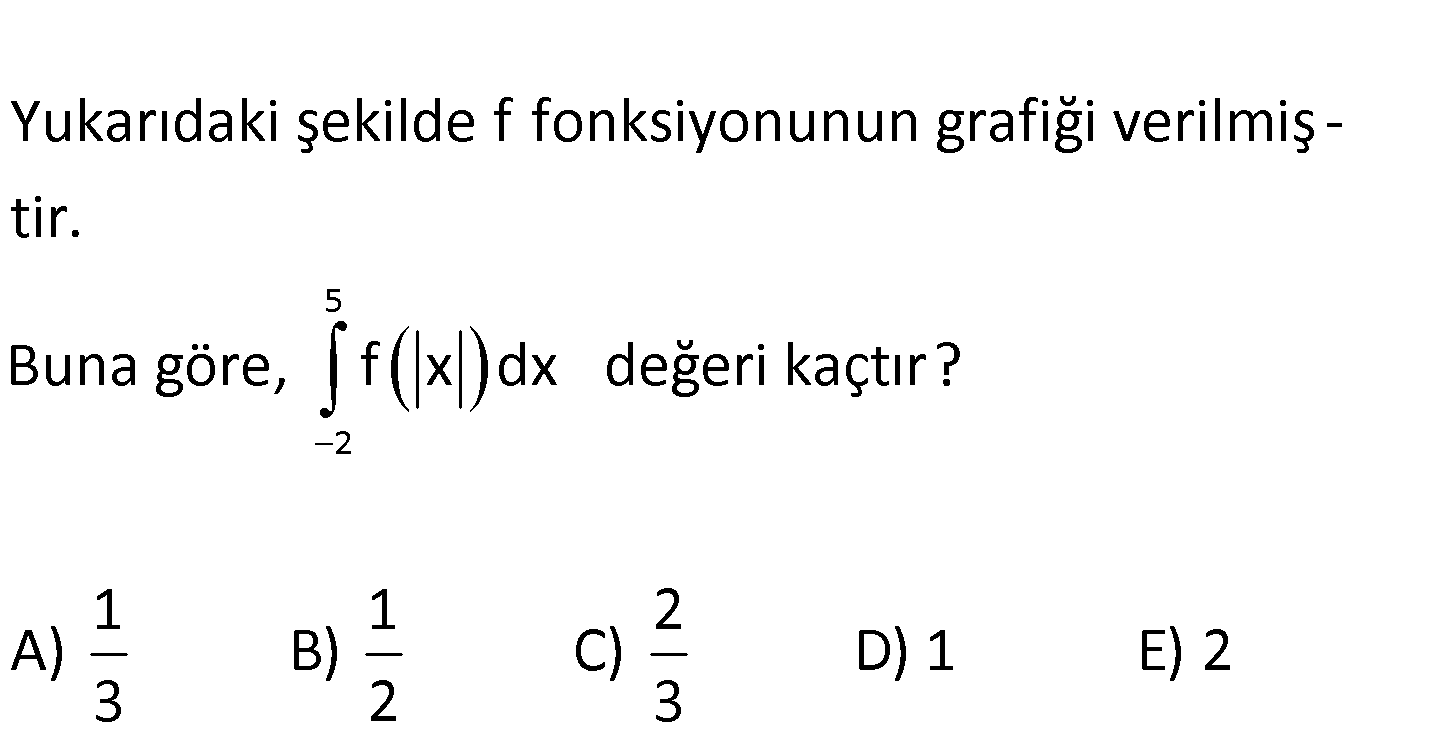
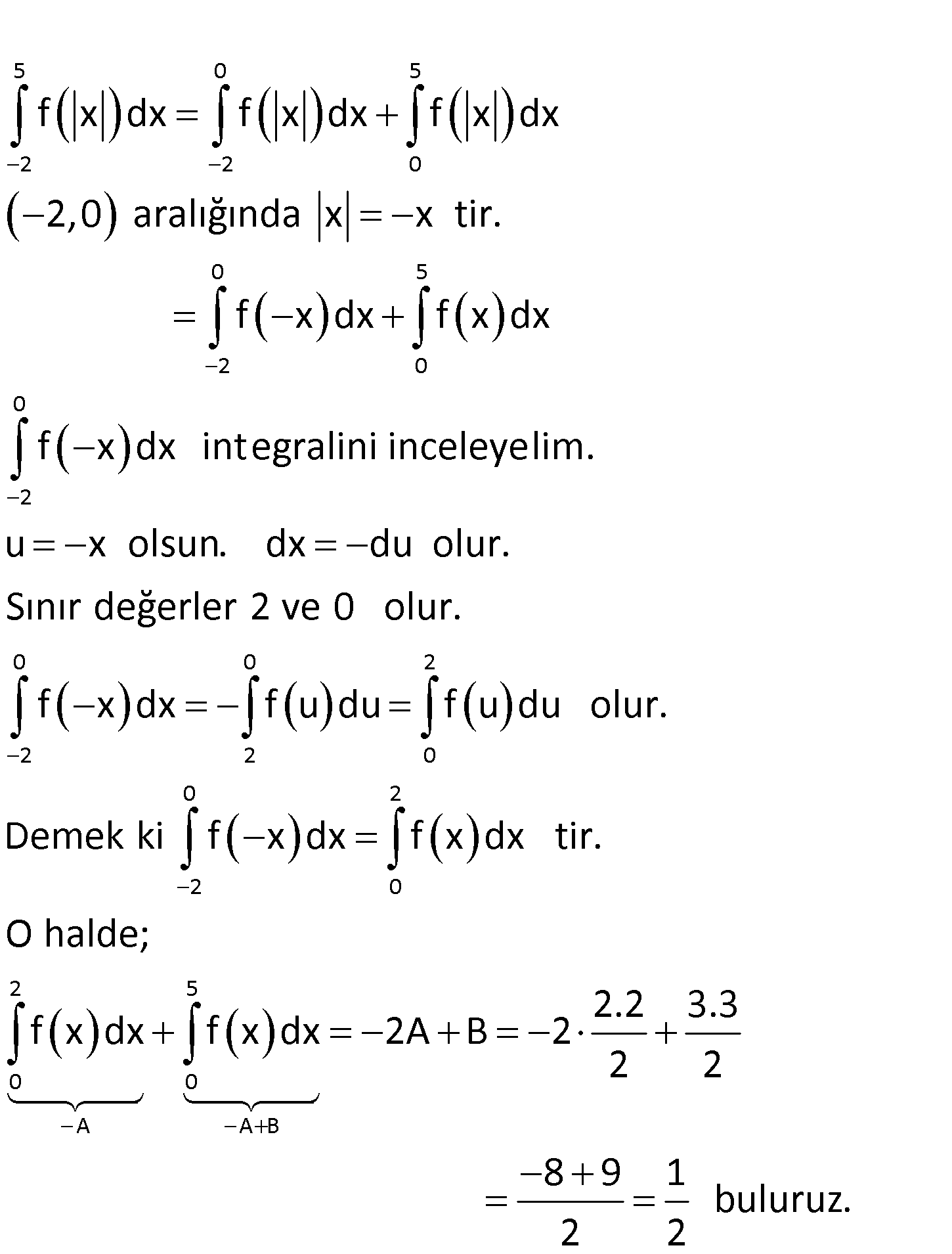
Diğer Soru Tipleri için Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
2 1 2 3 2 1 S S 30 ve f(x)dx 4 olduğuna göre, f(x)dx integralinin değeri kaçtır? A) 20 B) 16 C) 12 D) 16 E) 20 2 1 2 3 1 2 1 2 1 1 2 2 2 1 f(x)dx S S 4 S S 4 S S 36 2S 40 S 20 S 16 dır. f(x)dx S 16 : Çözüm buluruz. www.matematikkolay.net 58
www.matematikkolay.net 2 1 f : R R fonksiyonunun grafiği şekilde verilmiştir. Buna göre, (1 f( x))dx ifadesinin değeri k açtır? A) 2 B) 3 C) 4 D) 5 E) 6 2 1 2 2 1 1 (1 f( x))dx 1.dx f( x)dx (u x olsun, Sınırlar 1 ve : Çözüm 2 2 1 1 2 1 1 2 2 olur.) x f(u).( du) 2 ( 1) f(u)du (Sınırları Takla attıralım) 3 f(u)du 1 1 3 A B C 3 1 4 buluruz. 2 2 11
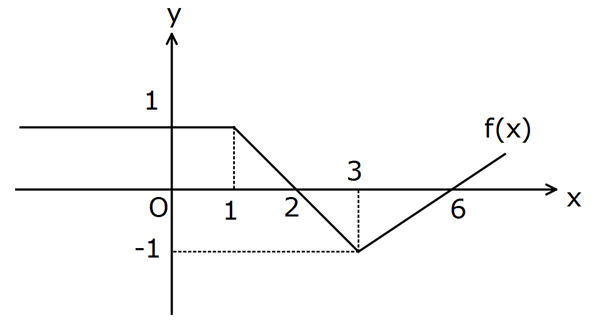
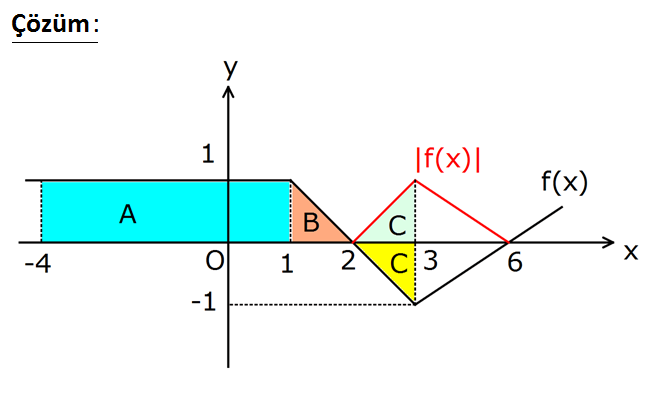
www.matematikkolay.net 1 3 4 1 Yukarıdaki grafik f(x) fonksiyonuna aittir. Buna göre, f(x)dx f(x)dx f(x) dx işleminin sonucu n edir? A) 10 B) 8 C) 6 D) 4 E) 2 İntegrallerin sonucu verilen aralıkta grafiğin altında kalan alanlar toplamına eşittir.x eksenini 1 3 4 1 1 3 3 4 1 1 A B C B C n üzerinde , x ekseninin altında kabul edilir. f(x)dx (f(x) f(x) )dx f(x)dx f(x)dx f(x) dx A B C B C A 2C 5.1 2 01.Oca . 2 51 4 bulunur. 18
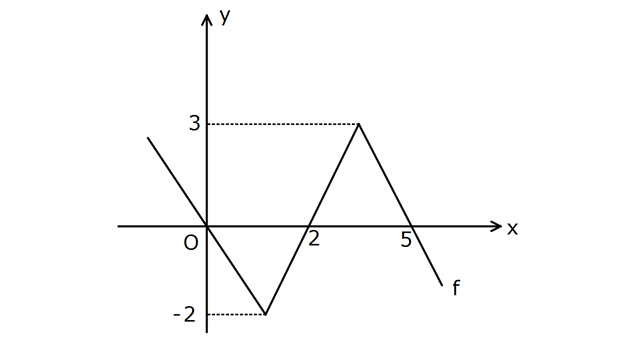
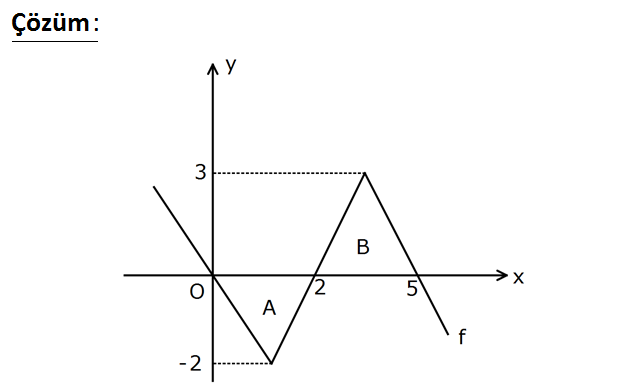
5 2 Yukarıdaki şekilde f fonksiyonunun grafiği verilmiş – tir. Buna göre, f x dx değeri kaçtır? 1 A) B 3 1 2 ) C) D) 1 E) 2 2 3 : Çözüm www.matematikkolay.net 5 0 5 2 2 0 0 5 2 0 0 2 f x dx f x dx f x dx 2,0 aralığında x x tir. f x dx f x dx f x dx i 0 0 2 2 2 0 0 2 2 0 2 5 0 0 A A B ntegralini inceleyelim. u x olsun. dx du olur. Sınır değerler 2 ve 0 olur. f x dx f u du f u du olur. Demek ki f x dx f x dx tir. O halde; 02.Şub f x dx f x dx 2A B 2 03.Mar 2 2 8 9 1 buluruz. 2 2 33

