Soru Sor sayfası kullanılarak Belirsiz İntegral konusu altında Üniversite Seviyesi İntegral Soruları ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU

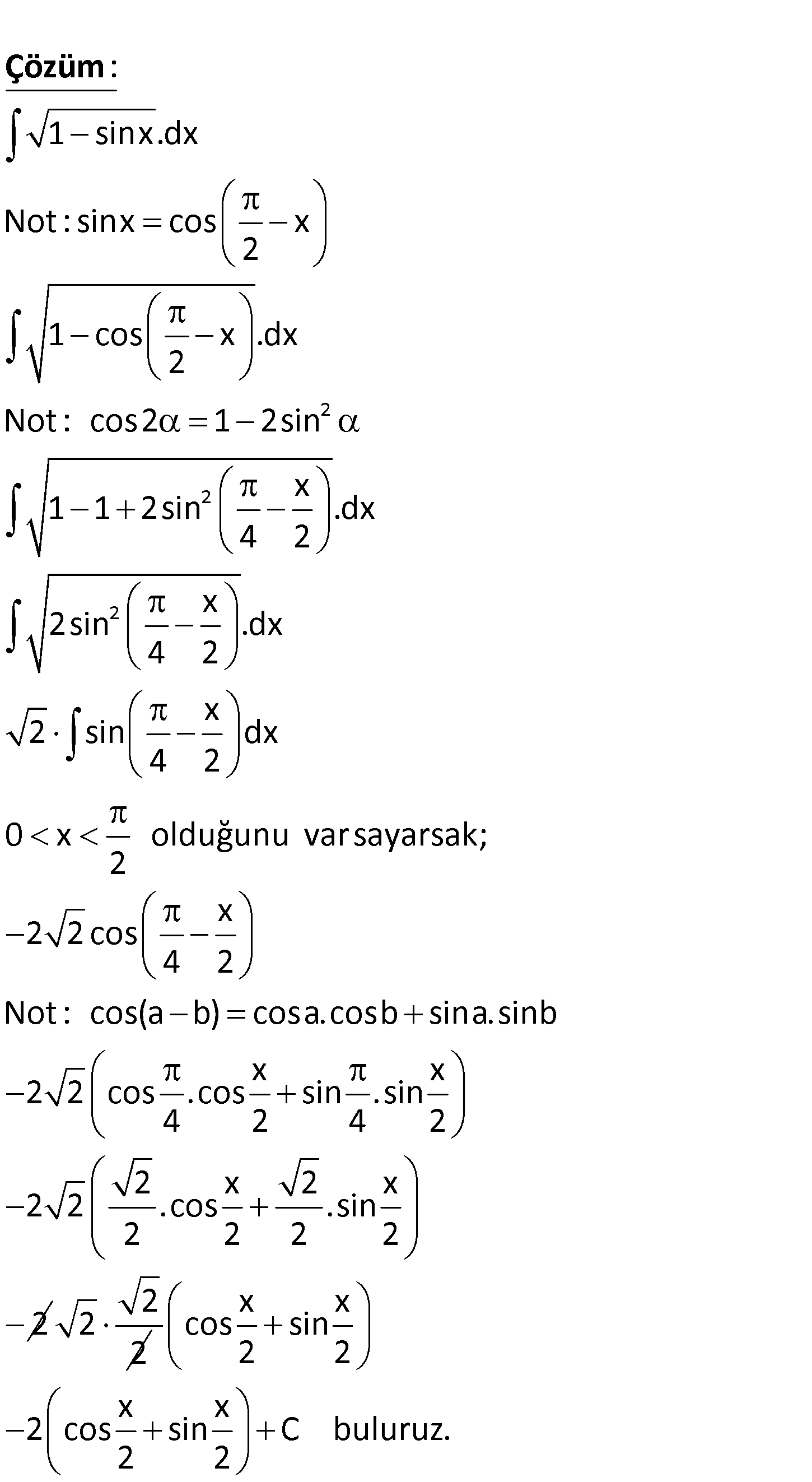
2.SORU


3.SORU
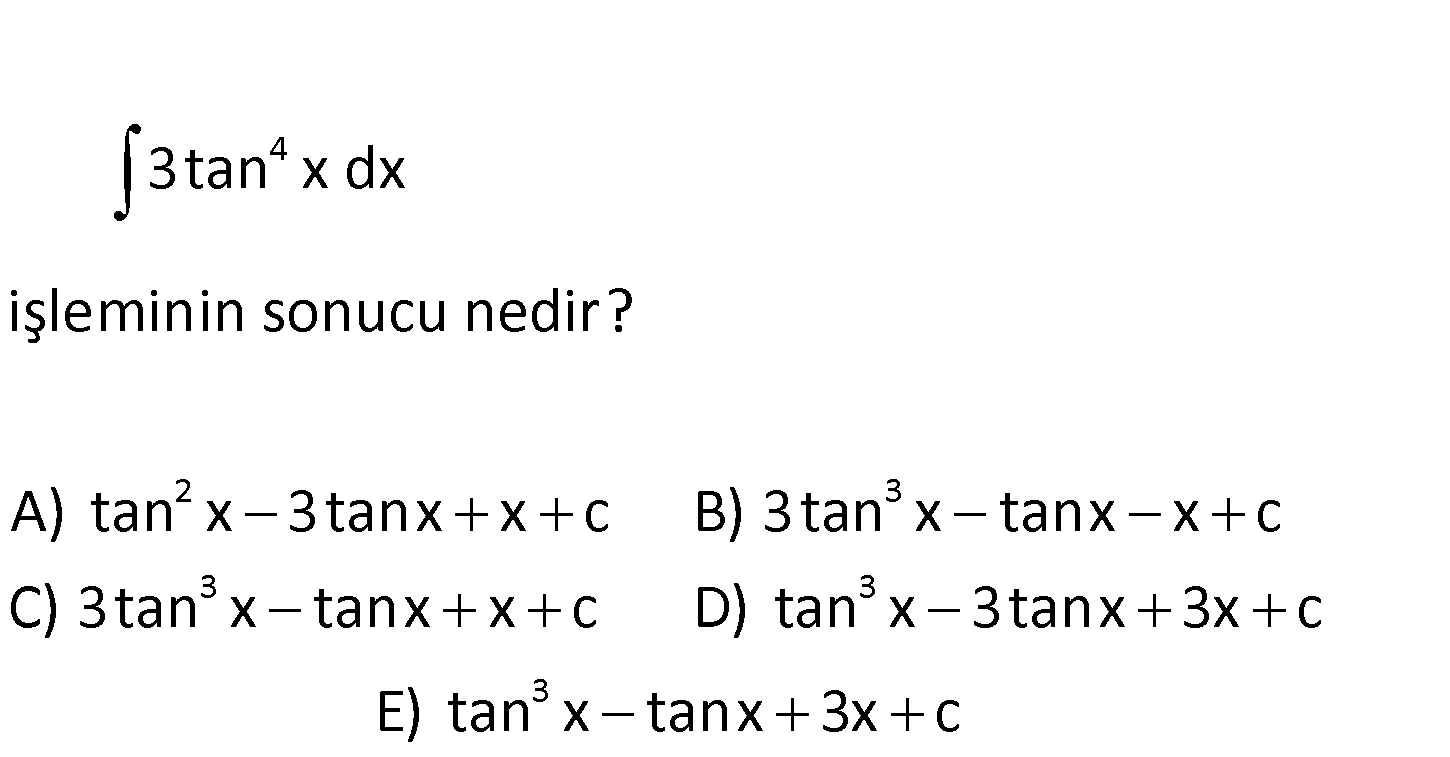
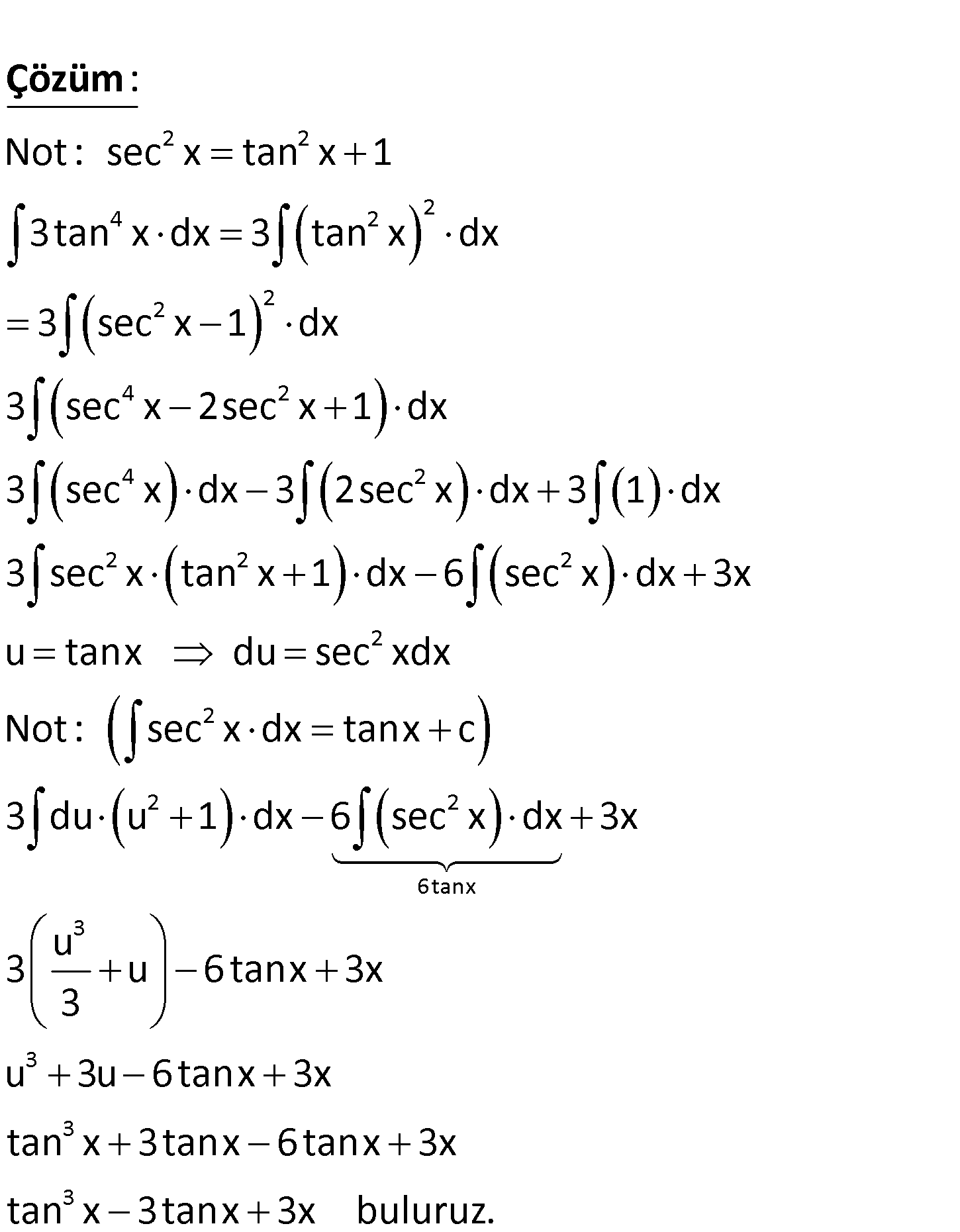
4.SORU

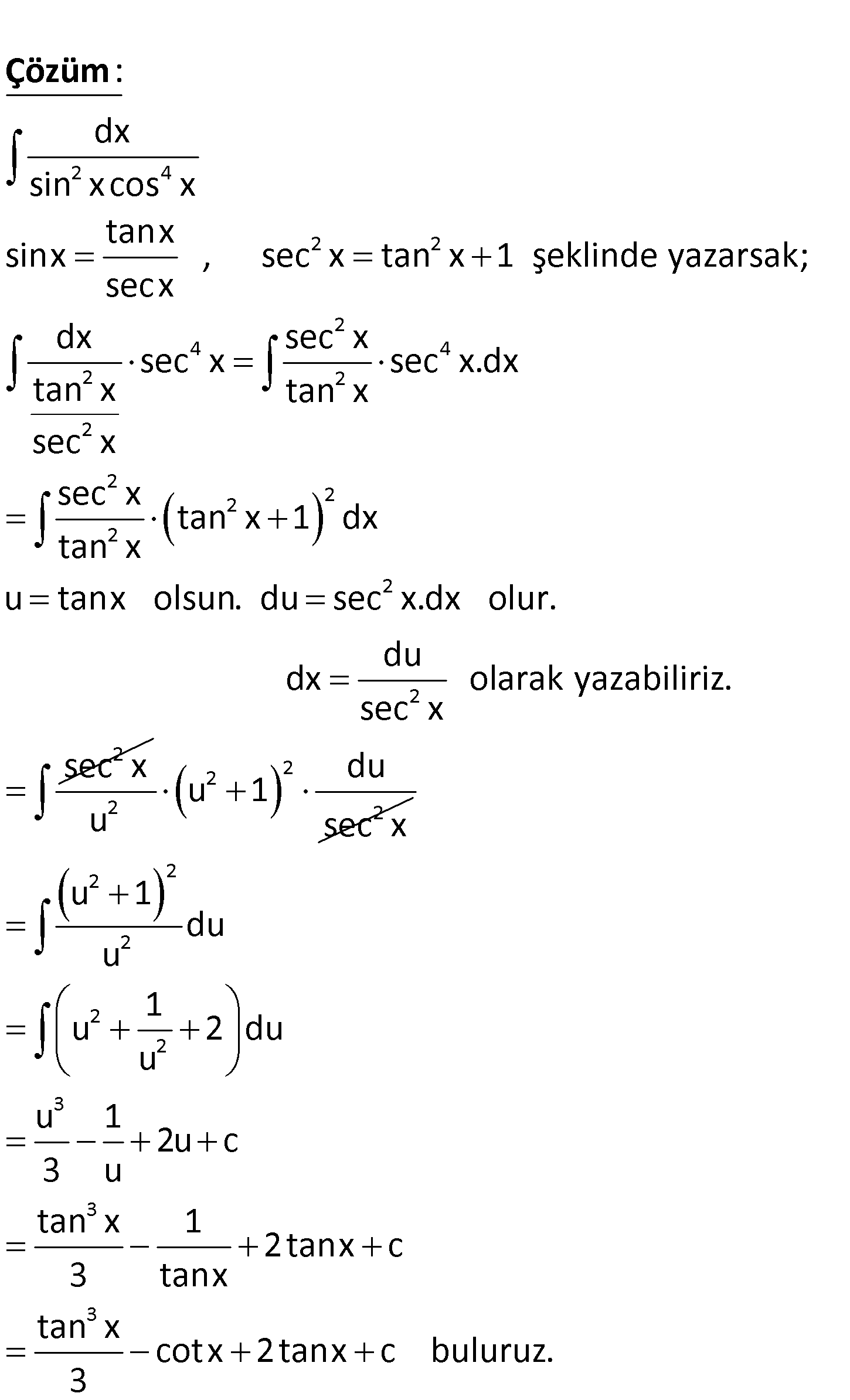
5.SORU
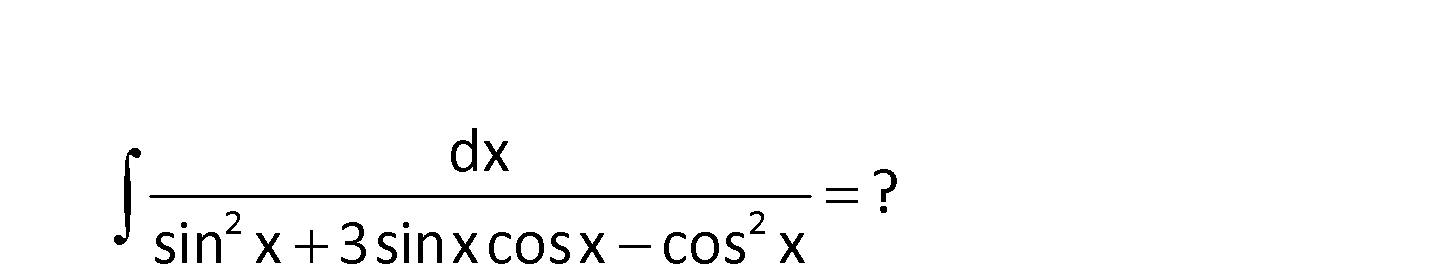
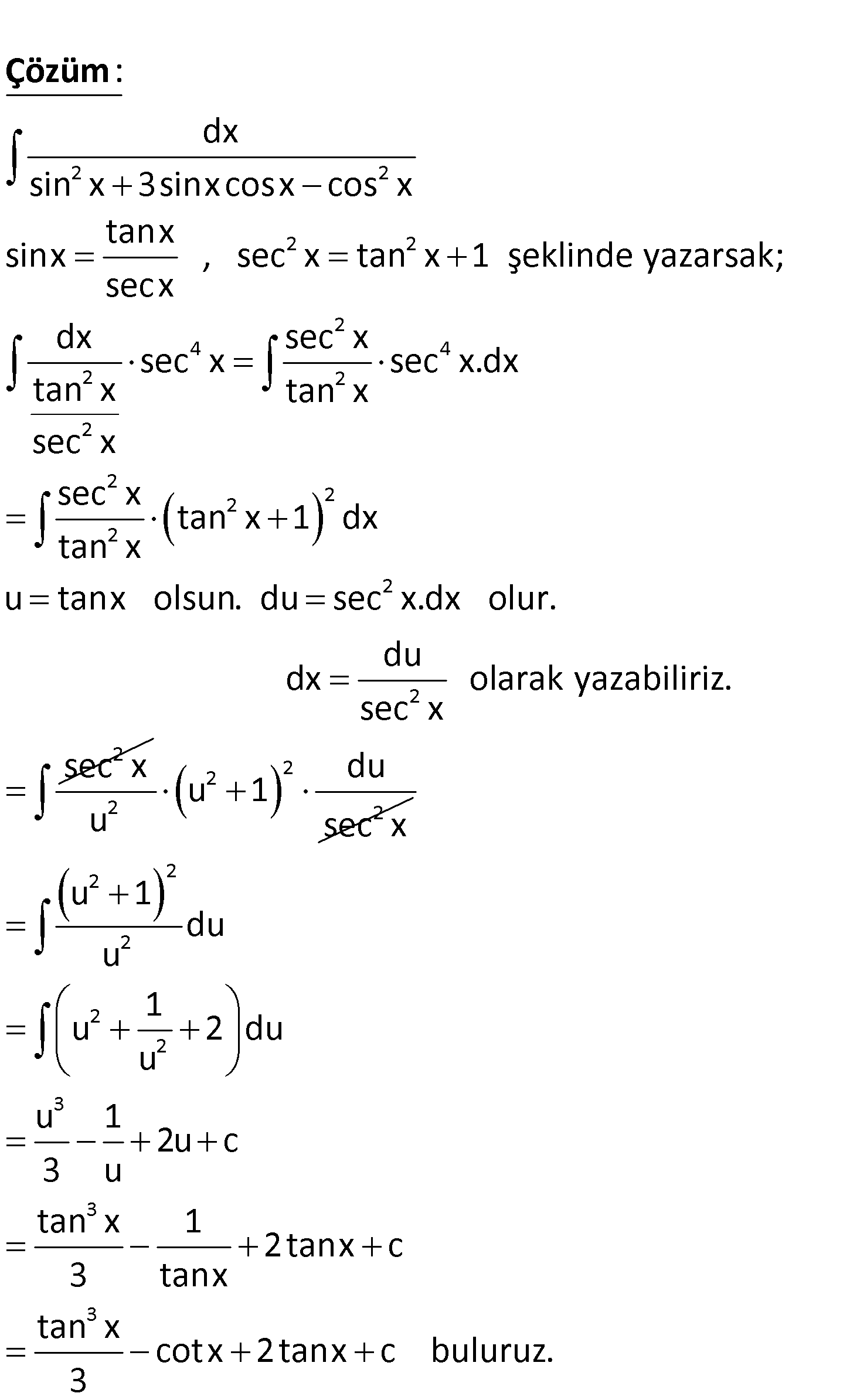
6.SORU
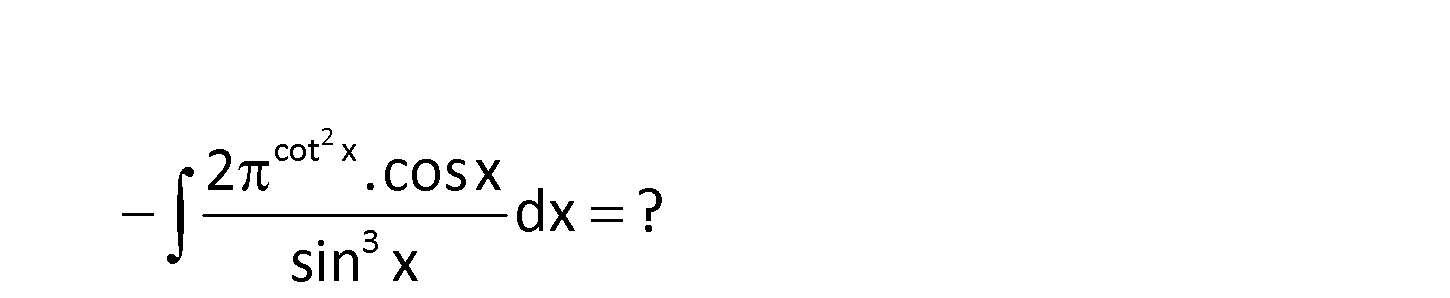

7.SORU
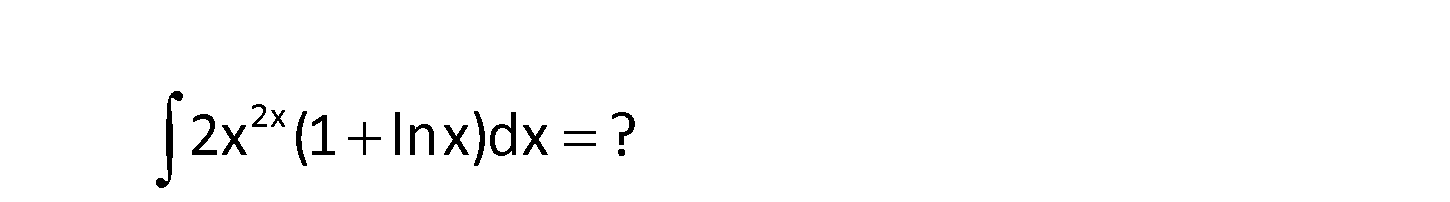

8.SORU


Diğer Soru Tipleri için Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
1sinx dx ? 2 2 1 sinx.dx Not : sinx cos x 2 1 cos x .dx 2 Not : cos2 1 2sin x 1 1 2si : n .d 4 2 Çözüm 2 x x 2sin .dx 4 2 x 2 sin dx 4 2 0 x olduğunu var sayarsak; 2 x 2 2 cos 4 2 Not : cos(a b) cosa.cosb sina.sinb x x 2 2 cos .cos sin .sin 4 2 4 2 2 x 2 x 2 2 .cos .sin 2 2 2 2 2 2 2 2 x x cos sin 2 2 x x 2 cos sin C buluruz. 2 2 www.matematikkolay.net 97
www.matematikkolay.net secx dx işleminin sonucu nedir? A) ln secx tanx c B) ln secx cotx c C) ln secx tanx c D) ln secx co tx c E) ln cosx tanx c 2 secx dx secx tanx Bu ifadeyi ile genişletelim. secx tanx secx tanx secx dx secx tanx sec x : Çözüm 2 2 secx tanx dx secx tanx u secx tanx olsun. du secx. tanx sec x olur. sec x secx tanx du dx secx tanx u lnu C ln secx tanx C 102
www.matematikkolay.net 4 2 3 3 3tan x dx işleminin sonucu nedir? A) tan x 3tanx x c B) 3tan x tanx x c C) 3tan x tanx x c D) t 3 3 an x 3tanx 3x c E) tan x tanx 3x c 2 2 4 2 2 2 2 4 2 4 2 Not : sec x tan x 1 3tan x dx 3 tan x dx 3 sec x 1 dx 3 sec x 2sec x 1 dx 3 sec x dx 3 2sec x : Çözüm 2 2 2 2 2 2 2 6tanx 3 3 3 3 dx 3 1 dx 3 sec x tan x 1 dx 6 sec x dx 3x u tanx du sec xdx Not : sec x dx tanx c 3 du u 1 dx 6 sec x dx 3x u 3 u 6tanx 3x 3 u 3u 6tanx 3x tan x 3tanx 6tanx 3x tan x 3tanx 3x buluru z. www.matematikkolay.net 104
2 4 dx ? sin xcos x 2 4 2 2 2 4 2 2 dx sin xcos x tanx sinx , sec x tan x 1 şeklinde yazarsak; secx dx sec x sec x tan x s c : e x Çözüm 4 2 2 2 2 2 2 2 2 sec x.dx tan x sec x tan x 1 dx tan x u tanx olsun. du sec x.dx olur. du dx olarak yazabiliriz. sec x sec x 2 2 2 2 du u 1 u sec x 2 2 2 2 2 3 3 3 u 1 du u 1 u 2 du u u 1 2u c 3 u tan x 1 2tanx c 3 tanx tan x cotx 2tanx c buluruz. 3 www.matematikkolay.net 107
2 2 dx ? sin x 3sinxcosx cos x 2 2 2 2 4 2 2 dx sin x 3sinxcosx cos x tanx sinx , sec x tan x 1 şeklinde yazarsak; secx dx sec ta x : n sec x Çözüm 2 4 2 2 2 2 2 2 2 2 sec x x sec x.dx tan x sec x tan x 1 dx tan x u tanx olsun. du sec x.dx olur. du dx olarak yazabiliriz. sec x sec x 2 2 2 2 du u 1 u sec x 2 2 2 2 2 3 3 3 u 1 du u 1 u 2 du u u 1 2u c 3 u tan x 1 2tanx c 3 tanx tan x cotx 2tanx c buluruz. 3 108
2 cot x 3 2 .cosx dx ? sin x www.matematikkolay.net 2 2 2 2 cot x 2 cot x cot x cot x 2 u olsun. du cot x ‘ .ln 2cotx. cotx ‘ .ln 1 2cotx. .l sin x : Çözüm 2 2 2 2 cot x 2 cot x 3 cot x cot x 3 n cosx 1 2 . .ln sinx sin x 2cosx . .ln dir. sin x Buna göre; 2 .cosx du u c c buluruz. sin x ln ln ln 127
2x 2x (1lnx)dx ? 2x 2x 2x 2x (1 lnx)dx değişken değişitirelim. du u x olsun. x (2lnx 2) dir.(*) dx : Çözüm 2x 2x 2x 2x 2x 2x Buna göre; 2x (1 lnx)dx 1.du u x C buluruz. Cevap: x C (*) x in türevinin x (2lnx 2) olduğunun detayı: u x lnu 2xlnx dur. Türev alalım. du 2lnx 2x u 2x 1 x du u.(2lnx 2) x (2lnx 2) www.matematikkolay.net 9
4 x dx ? x www.matematikkolay.net 2 4xdx xx4sint dönüşümü kullanalım.dx8.sint.cost.dt Buna gör:Çözüm2222e;4x44sintdx8.sint.cost.dtx4sint4(1sint)8.sint.cost.dt4sint42cost428.sint.cost.dtsintcostsint8.sintn1n22n22.cost.dt8.cost 1cost.sint8.cost 81dt 22tcost.cosvsint8 224t4.cost.sintx4sint dönüşümünü kullanmsinvn1ıştıkcosvdvcosvdvnnBuna göre;.sin22xxxt sint tarcsin422xcost1sint1 dir. Bunları yerleştirelim.44t4.cost.sintxxx4arcsin4.1242x4arcsin4xxC buluruz.2 www.matematikkolay.net 3

