Soru Sor sayfası kullanılarak Belirsiz İntegral konusu altında İntegralli fonksiyon soruları, İntegraldeki sabit değeri bulma, Türev denkleminden asıl fonksiyonu bulma ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU


2.SORU
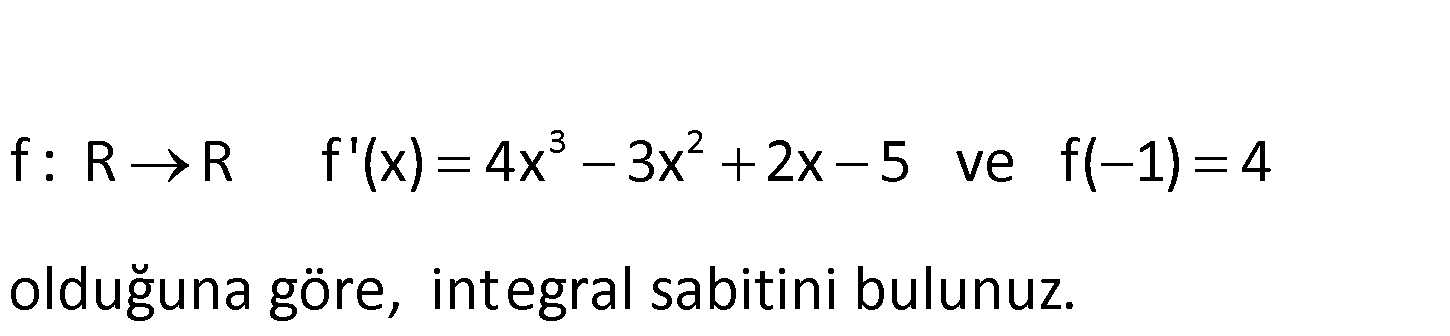
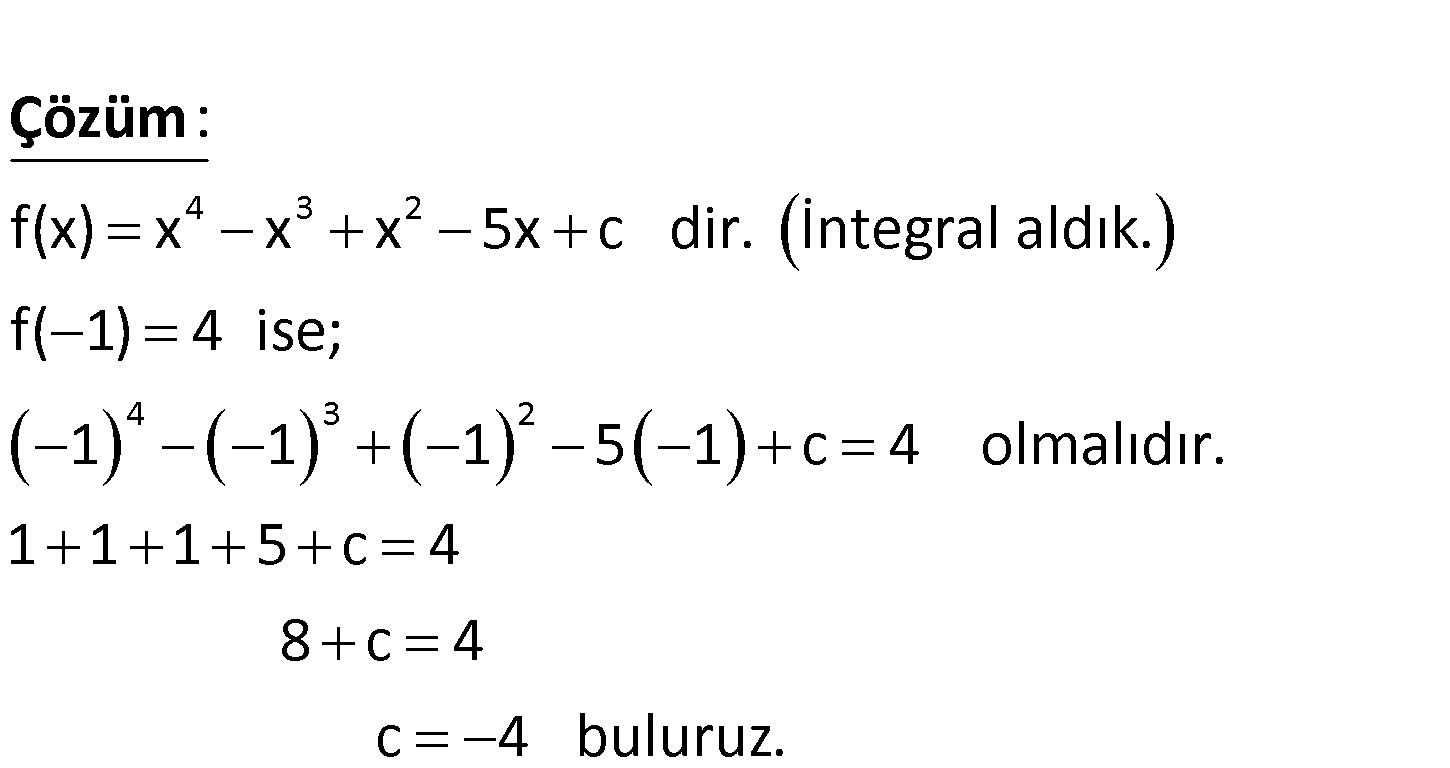
3.SORU


4.SORU
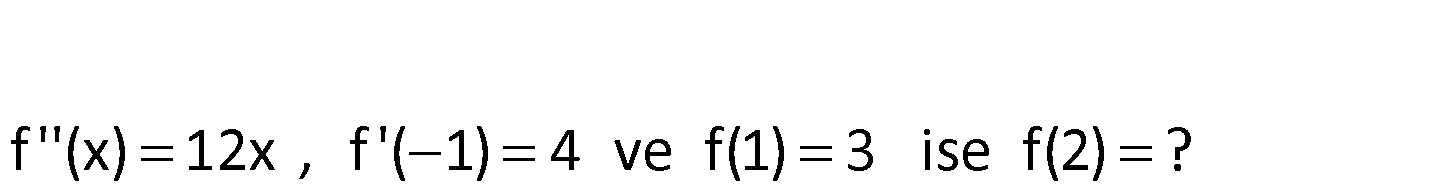

5.SORU
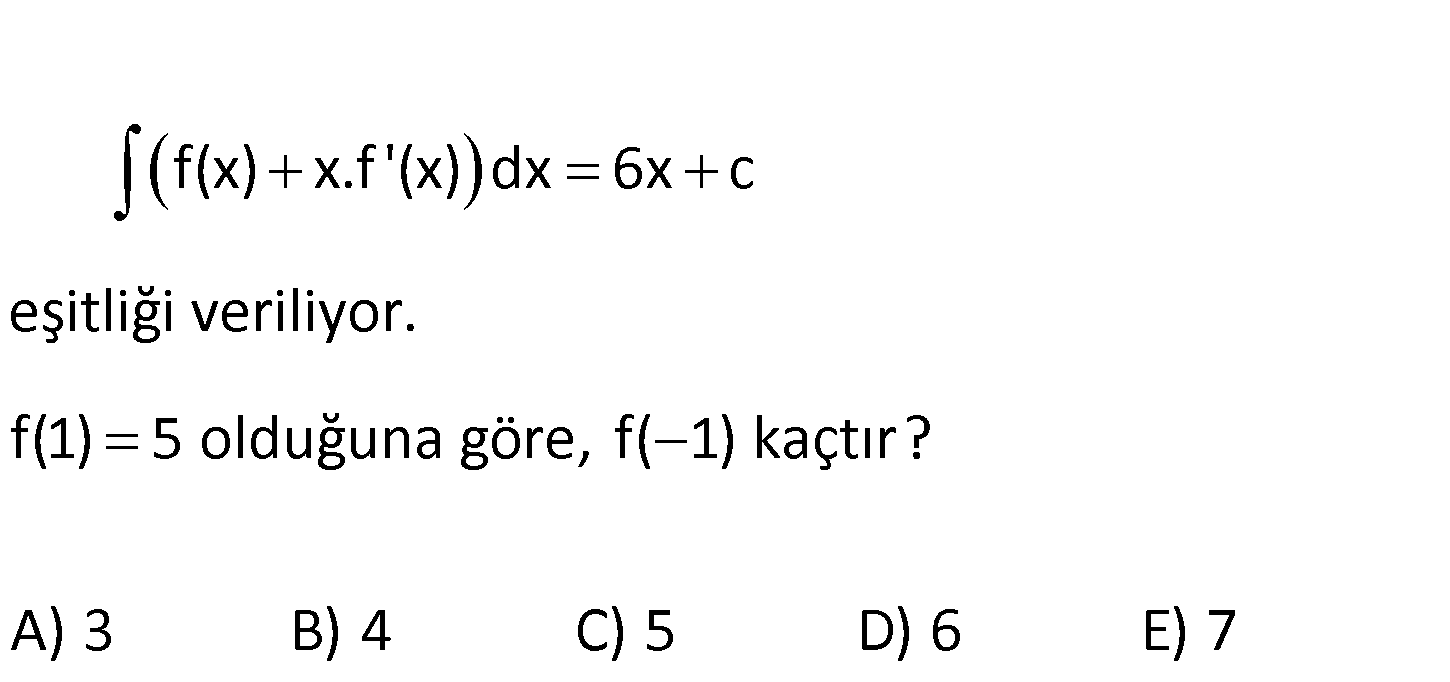
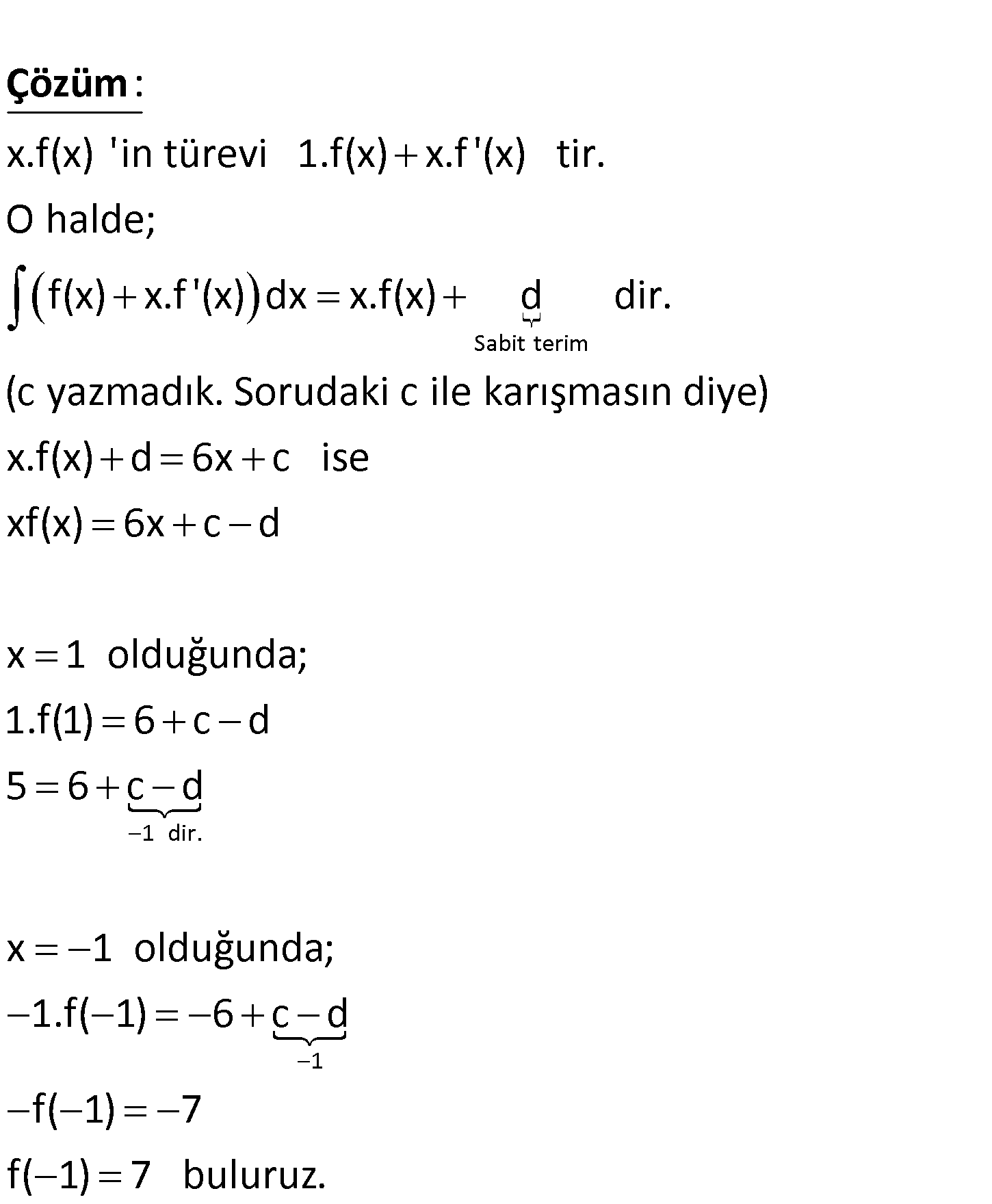
6.SORU


7.SORU

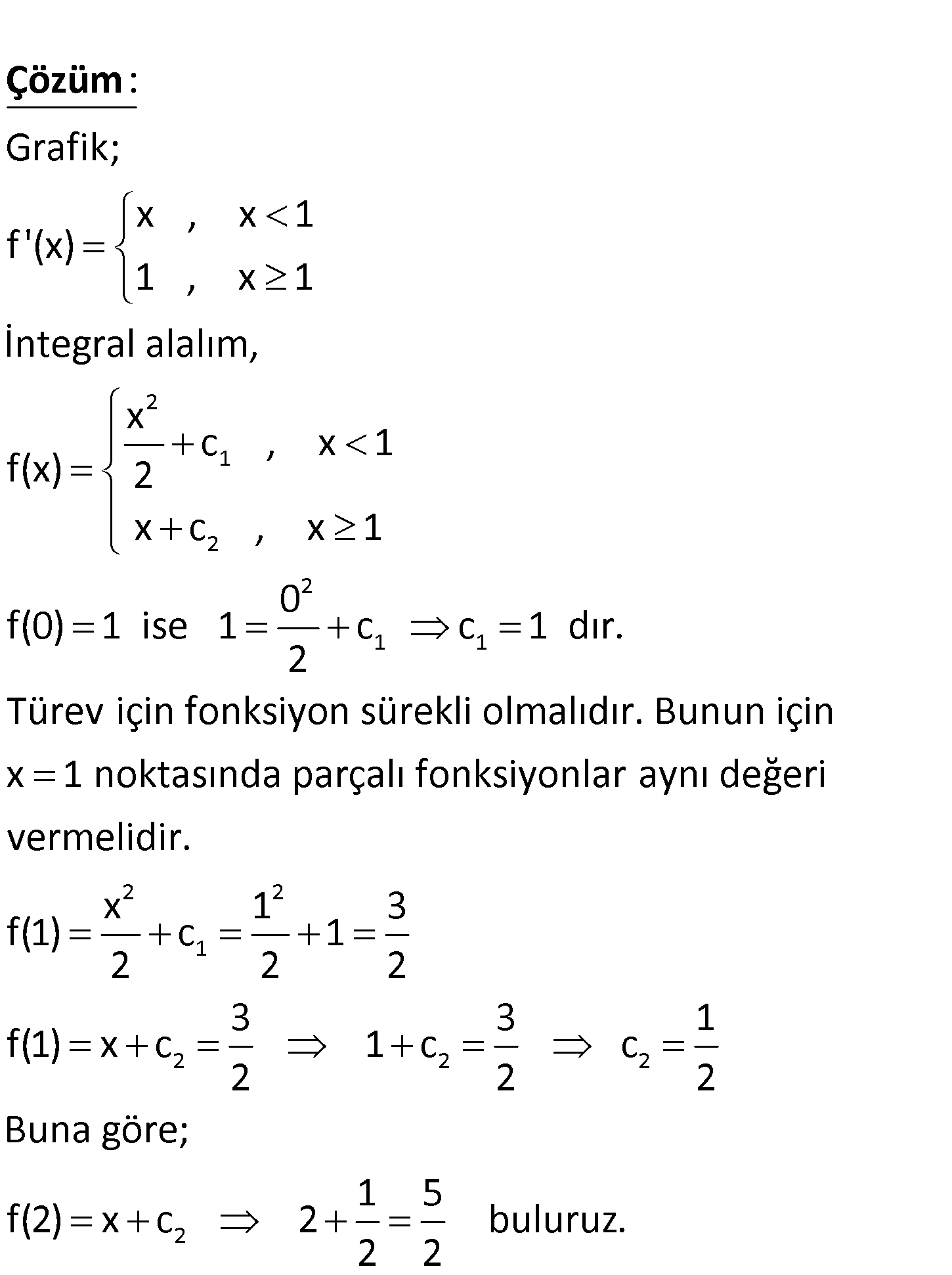
8.SORU

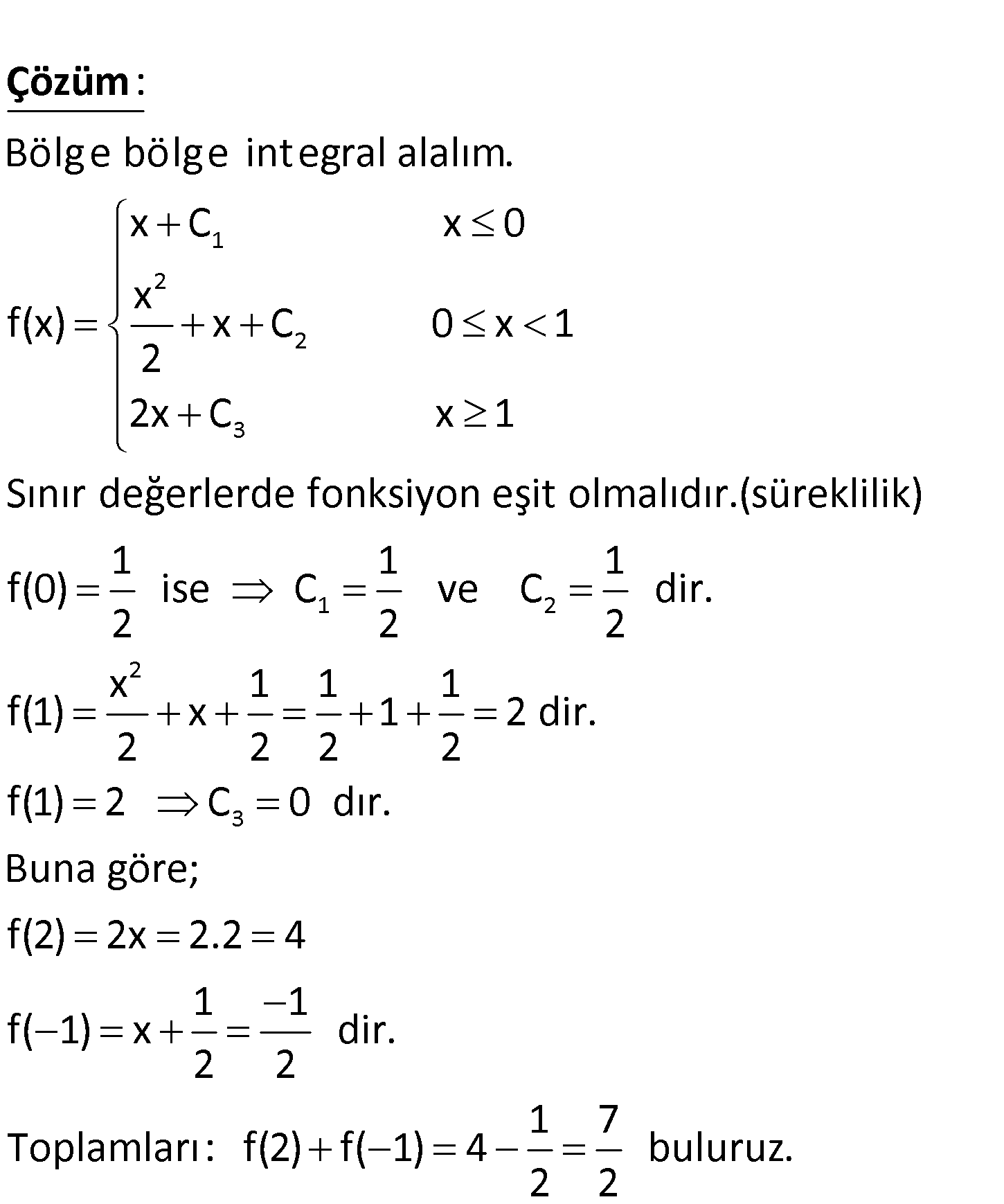
9.SORU
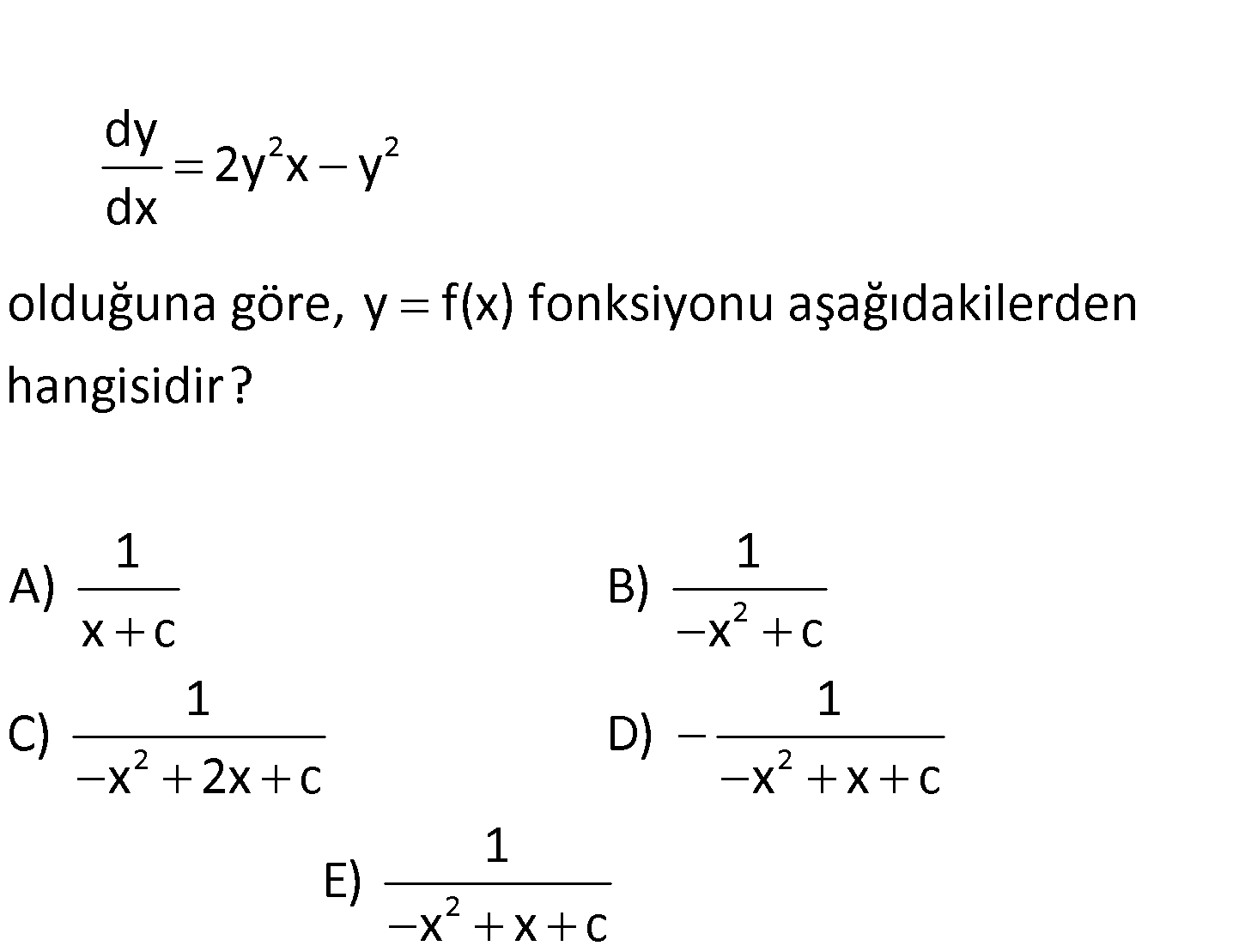

Burdan sonraki sorular, Fen Lisesi Müfredatı için geçerlidir.
10.SORU

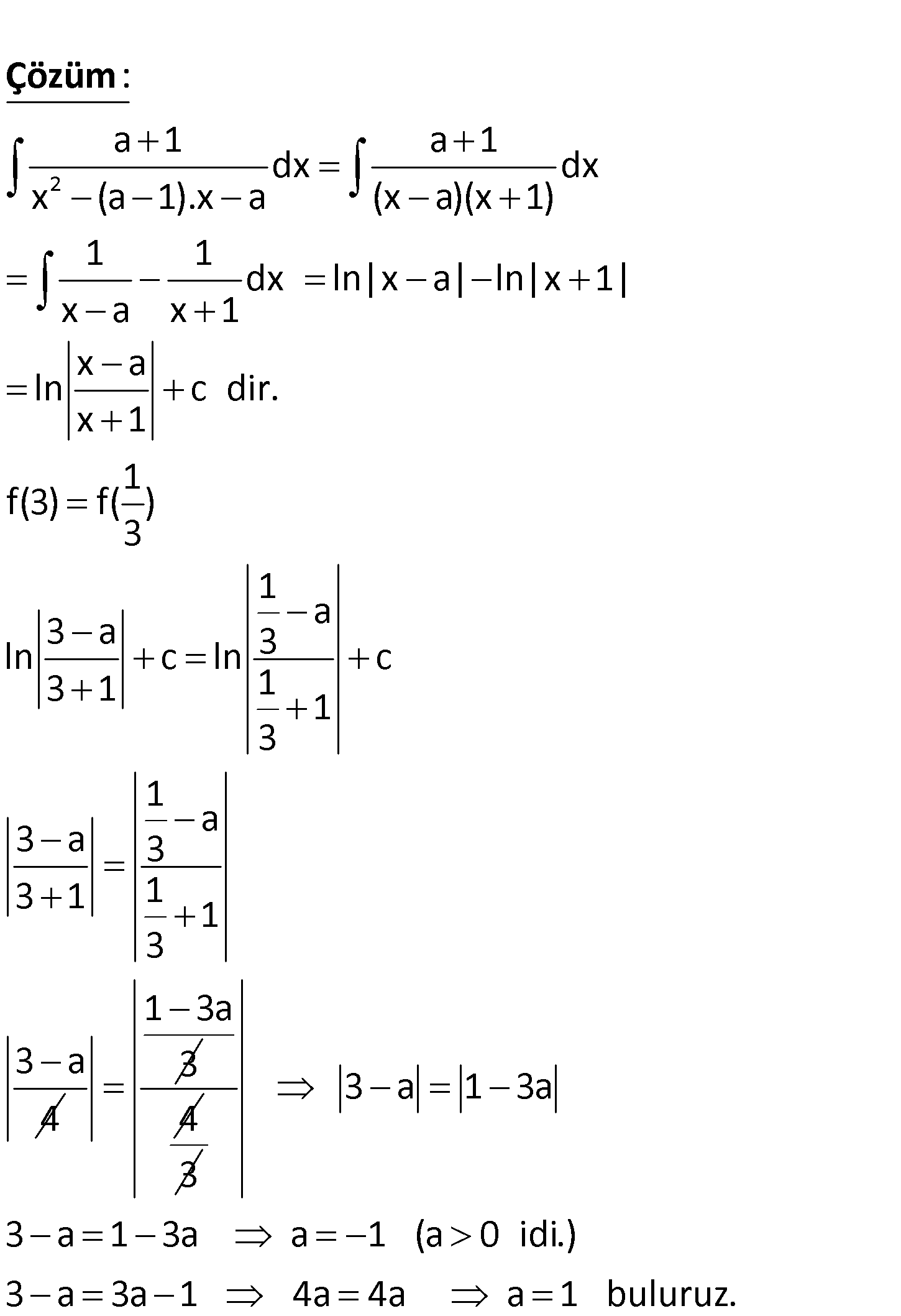
11.SORU
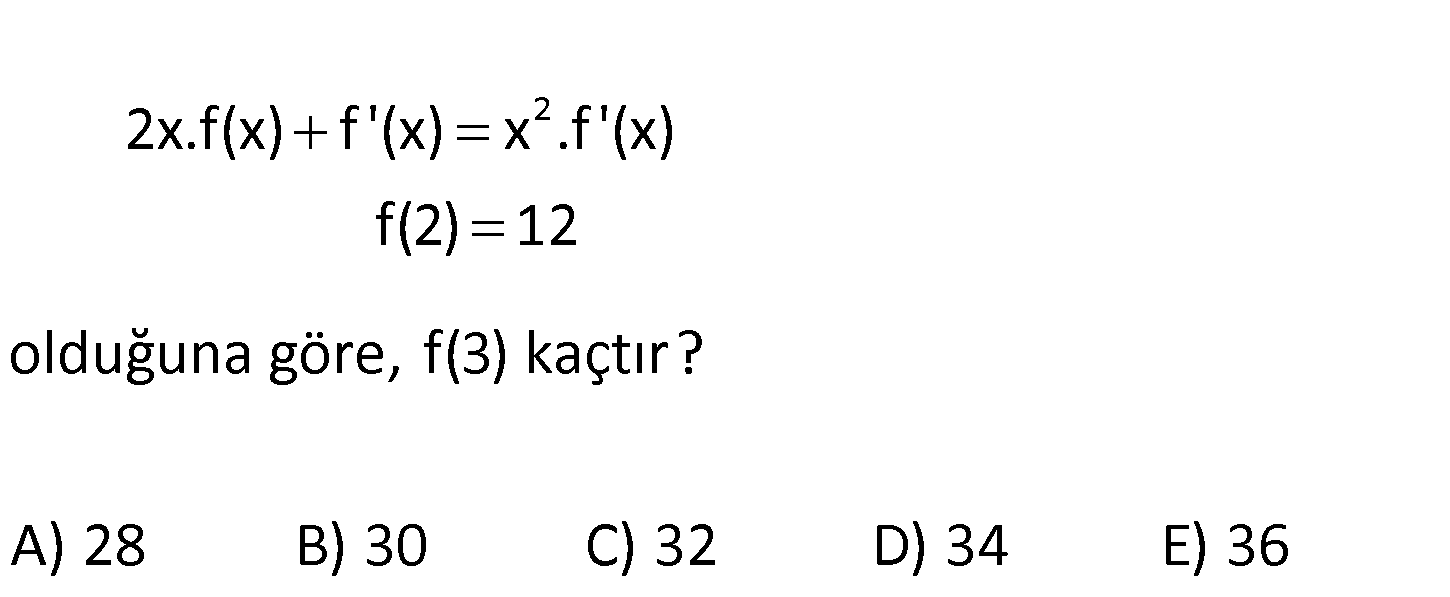
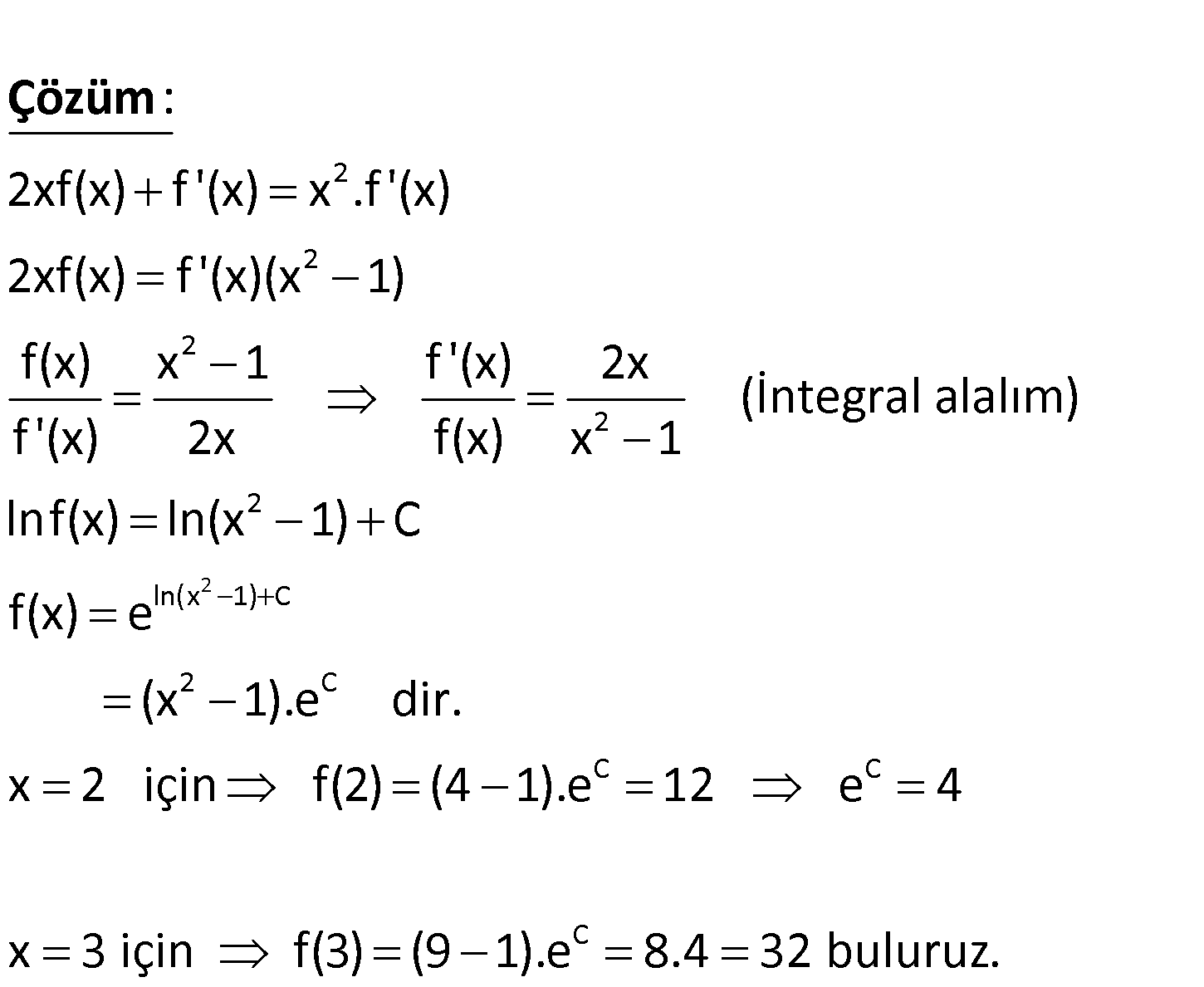
12.SORU
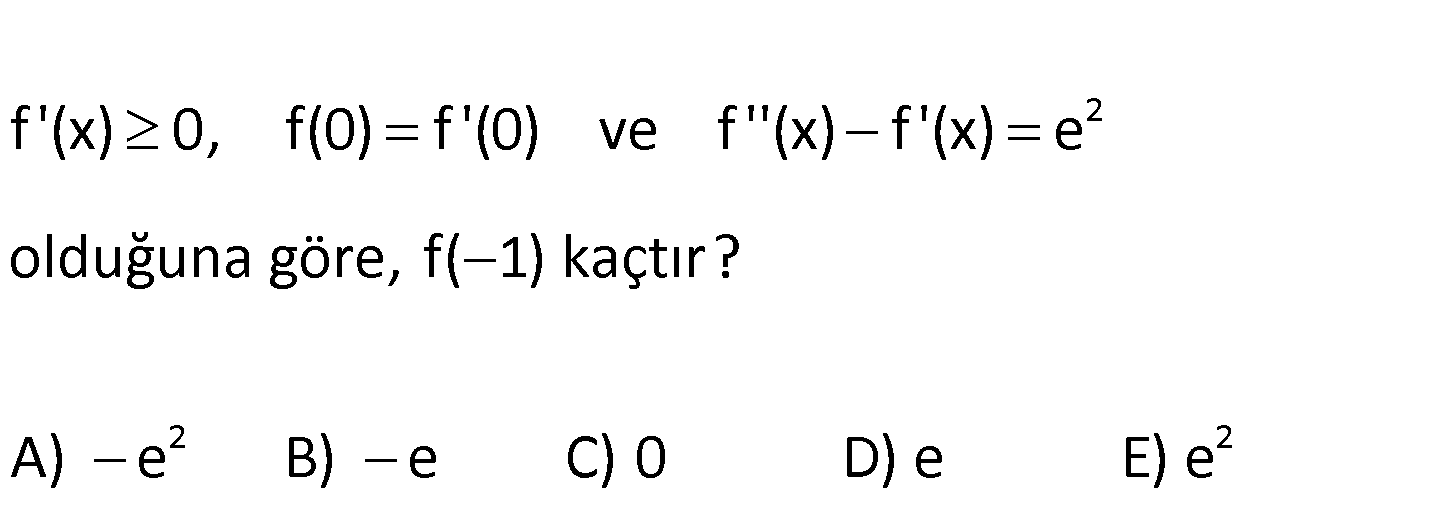

13.SORU
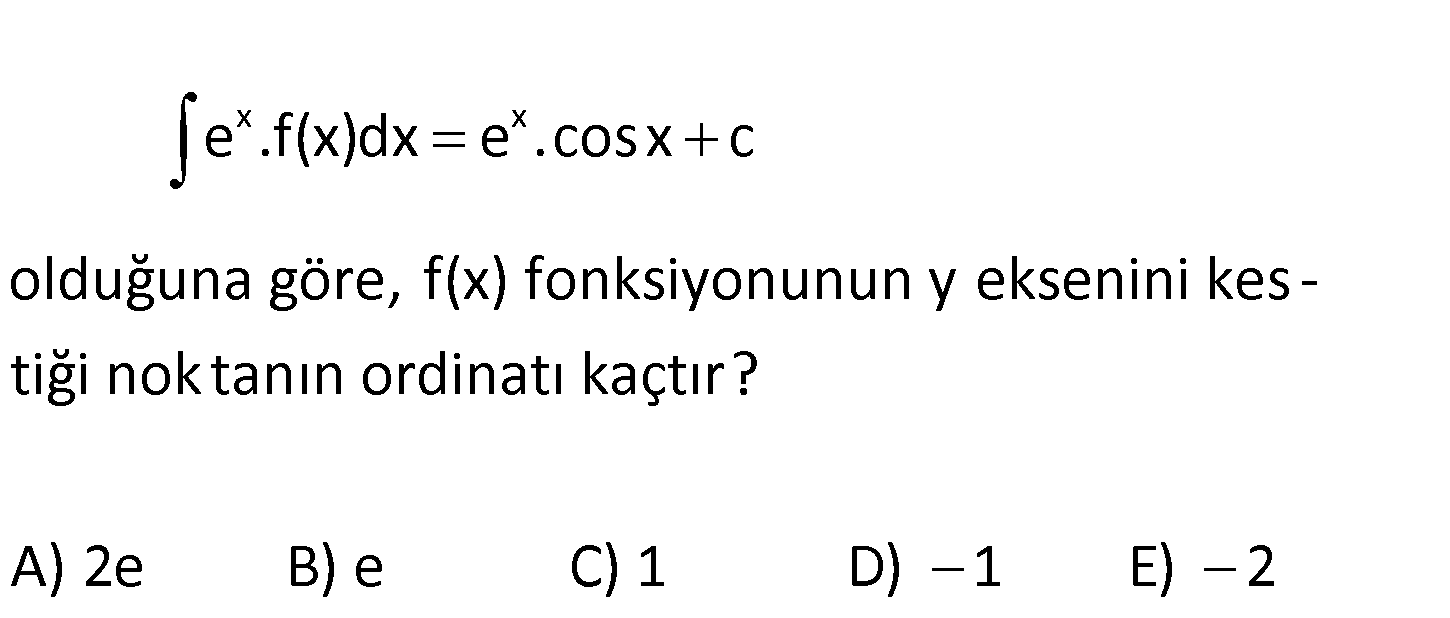
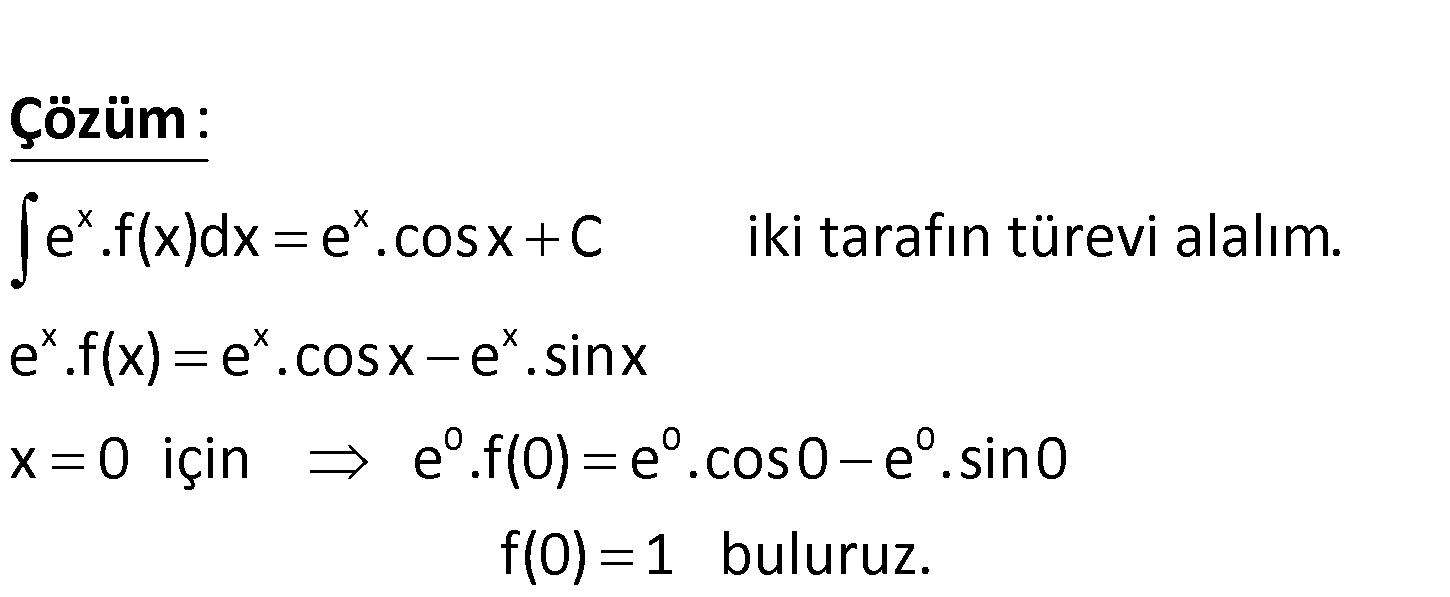
14.SORU
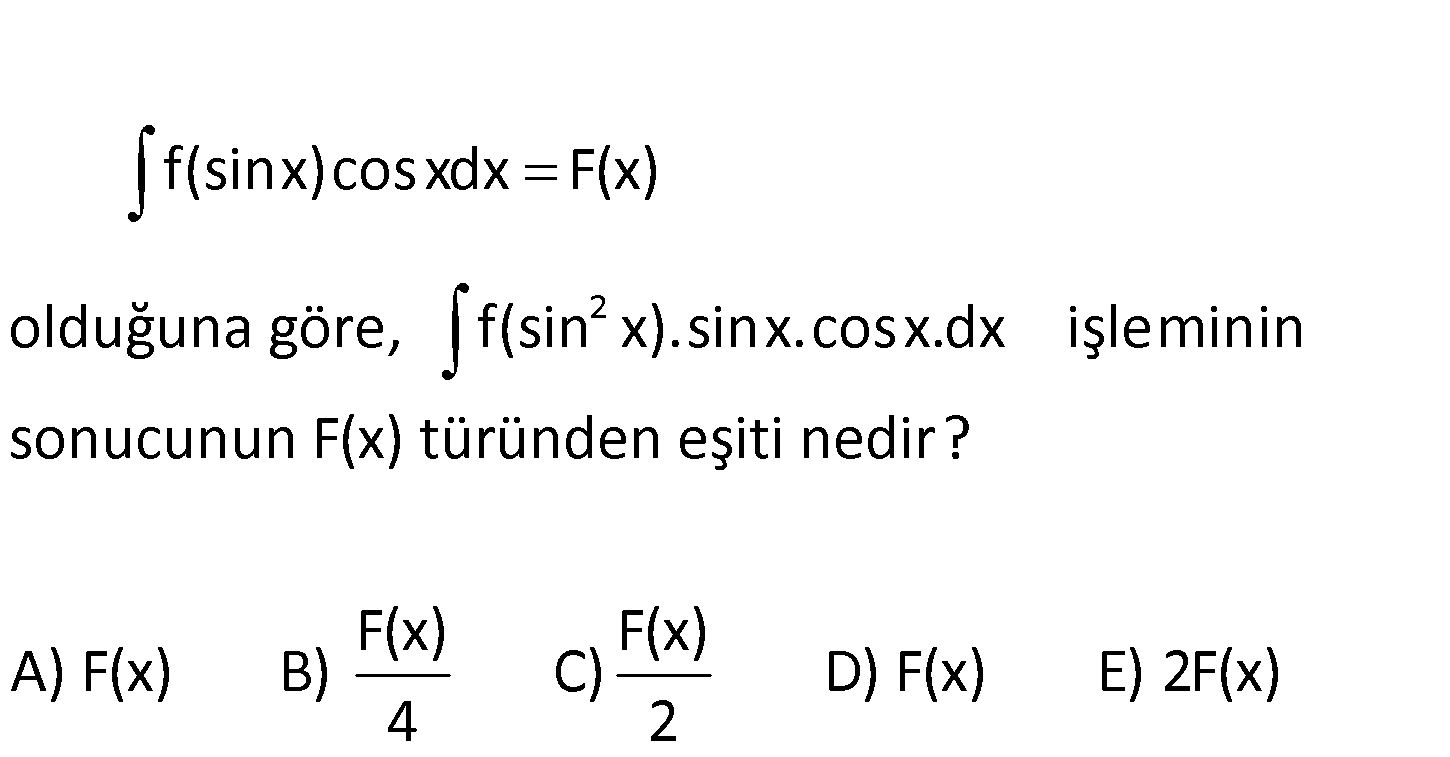
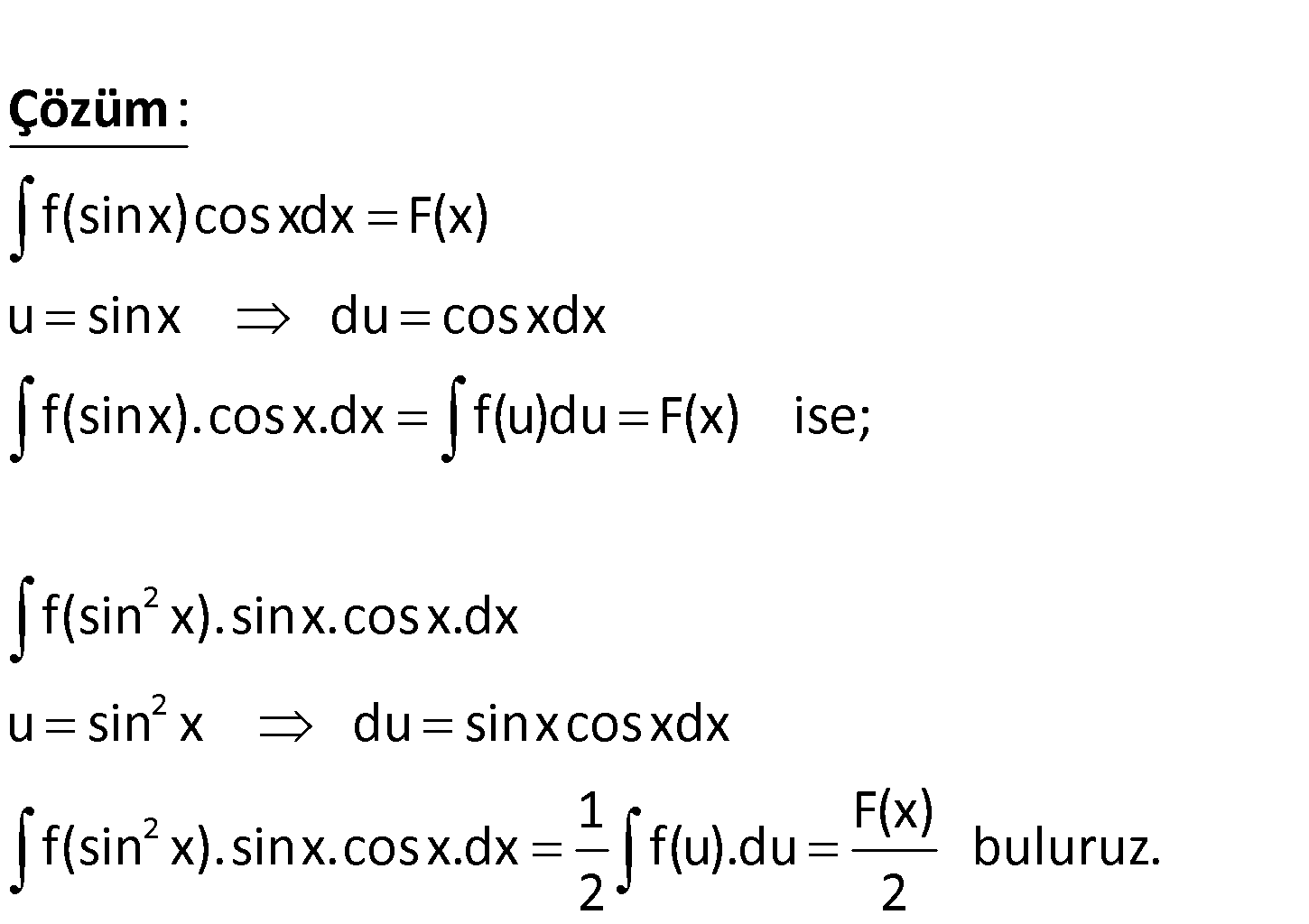
15.SORU
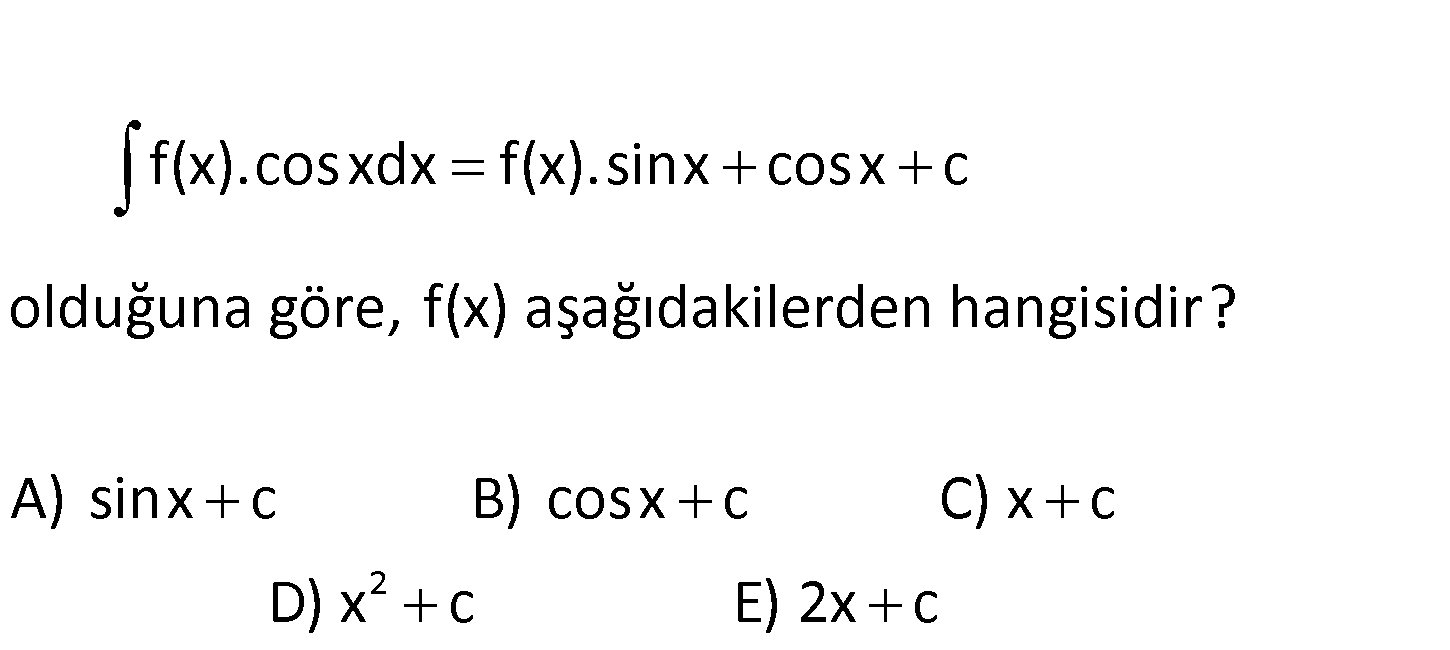

16.SORU
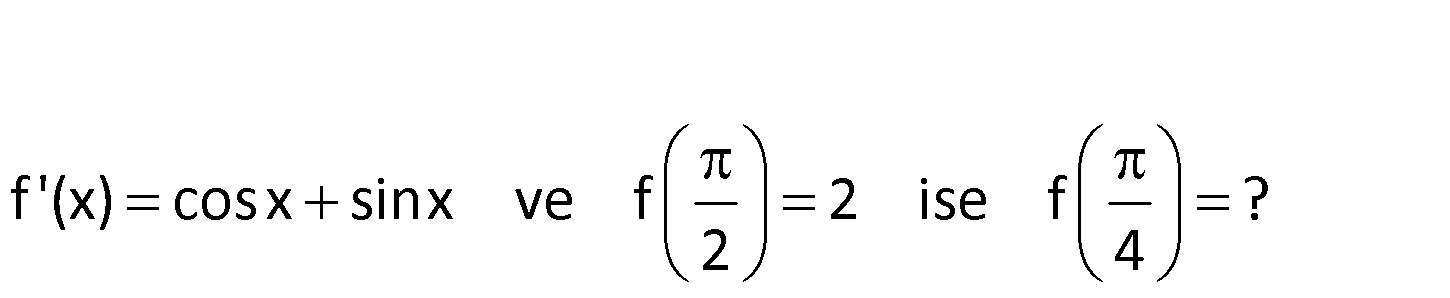
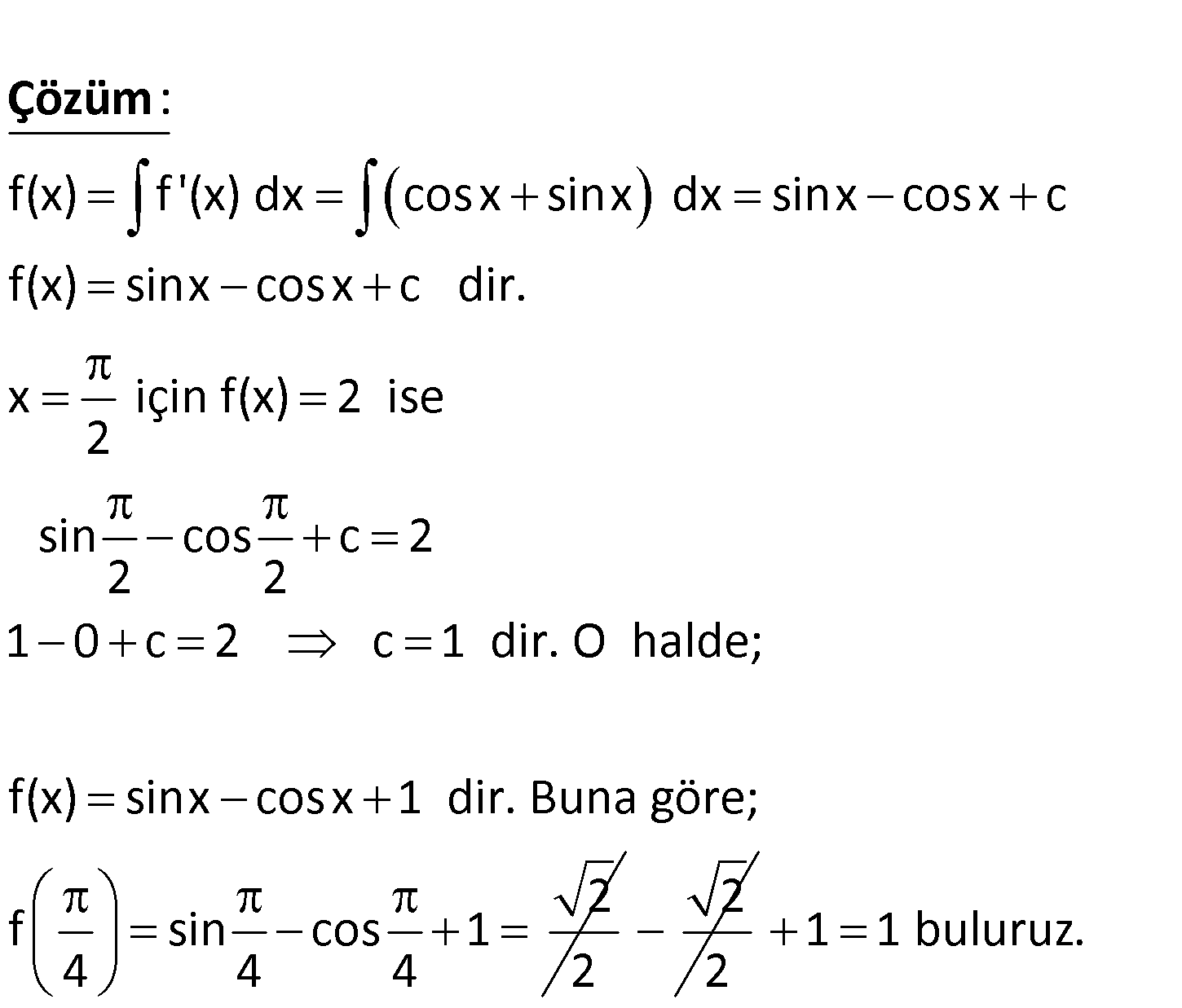
17.SORU
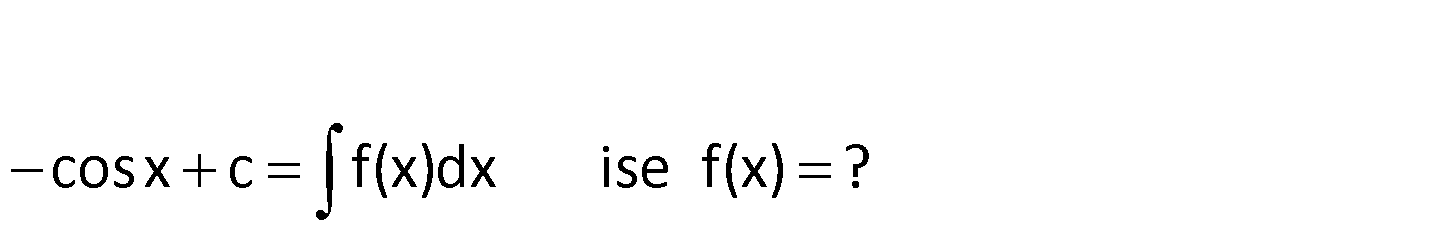
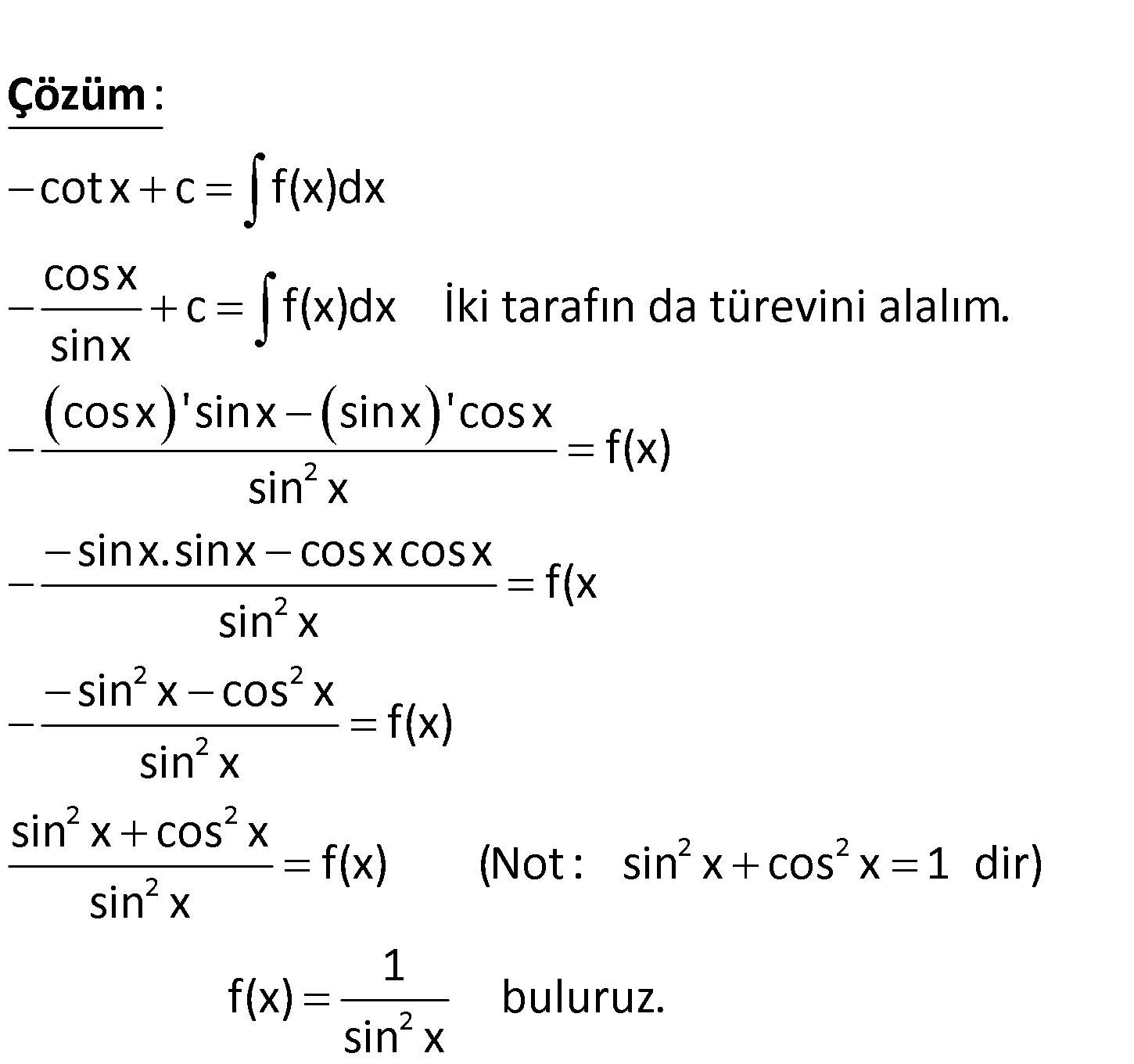
18.SORU
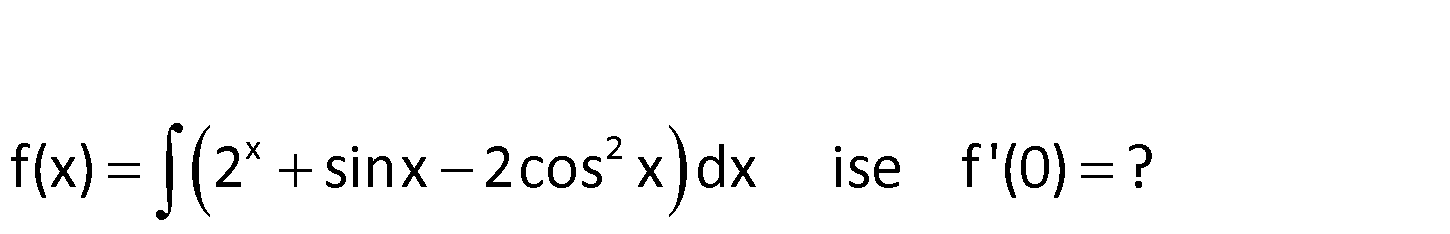

19.SORU
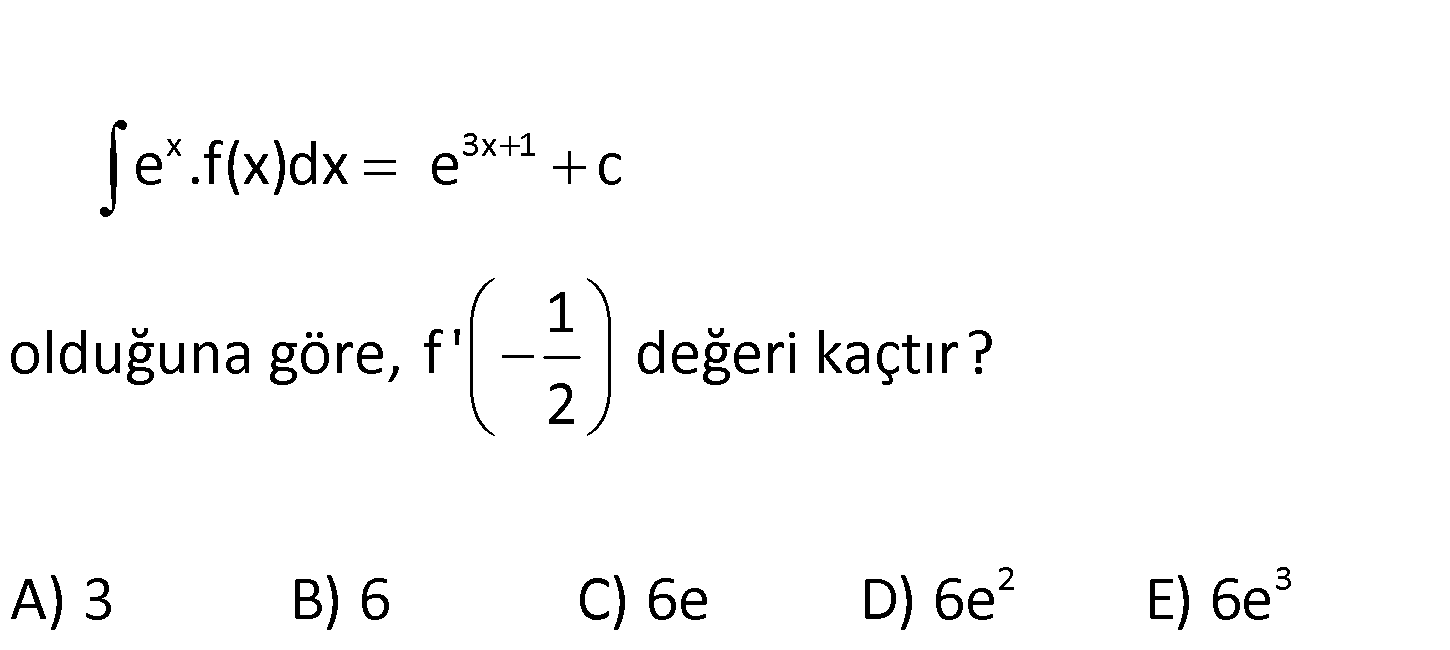

Diğer Soru Tipleri için Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
2 f(x) fonksiyonunun (1, 4) noktasındaki teğetinin eğimi 6 dır. f ”(x) 12x 4 olduğuna g öre, f( 1) kaçtır? A) 4 B) 6 C) 8 D) 10 E) 12 www.matematikkolay.net 2 2 3 f ”(x) 12x 4 f ”(x)dx (12x 4)dx f ‘(x) 4x 4x c (1,4) nokta : s Çözüm 3 3 3 3 4 2 4 2 4 2 ındaki eğim 6 ise f ‘(1) 6 dır. f ‘(x) 4x 4x c f ‘(1) 4.1 4.1 c 6 c 8 6 c 2 dir. f ‘(x) 4x 4x 2 dir. f ‘(x)dx (4x 4x 2)dx f(x) x 2x 2x d f(1) 4 f(1) 1 2.1 2.1 d 4 d 1 4 d 3 tür. f(x) x 2x 2x 3 f( 4 2 1) ( 1) 2( 1) 2( 1) 3 f( 1) 1 2 2 3 8 buluruz. 30
3 2 f : R R f ‘(x) 4x 3x 2x 5 ve f( 1) 4 olduğuna göre, integral sabitini bulunuz. www.matematikkolay.net 4 3 2 4 3 2 f(x) x x x 5x c dir. İntegral aldık. f( 1) 4 ise; 1 1 1 5 1 c 4 olmalıdır. 1 1 1 : Çözüm 5 c 4 8 c 4 c 4 buluruz. 71
f(x) fonksiyonunun grafiğinin üzerindeki (1, 3) nok – tasındaki teğetinin eğimi 3 ve f ‘(x) 2x a olduğuna göre, f(2) kaçtır? f ‘(1) 3 tür. Teğetin eğimi f ‘(x) 2x a denkleminde x 1 yazarsak; f ‘(1) 2 a 3 a 1 buluru : Çözüm 2 2 2 2 z. f ‘(x) 2x 1 ise; f(x) x x c dir. İntegral aldık. 1,3 noktası fonkisyonun bir noktası olduğundan; f(1) 3 olmalıdır. f(1) 1 1 c 3 c 1 buluruz. f(x) x x 1 ise f( 2) 2 2 1 4 2 1 2 1 3 buluruz. C evap: 3 73
f ”(x) 12x , f ‘( 1) 4 ve f(1) 3 ise f(2) ? 2 2 f ”(x) 12x ise f ‘(x) 6x c dir. f ‘( 1) 4 ise f ‘( 1) 6 1 c 4 olmalıdır. : Çözüm 2 3 3 3 6 c 4 c 2 dir. f ‘(x) 6x 2 ise; f(x) 2x 2x c dir. f(1) 3 ise 2. 1 2. 1 c 3 2 2 c 3 c 3 tür. f(x) 2x 2x 3 olur. Buna göre; f(2) 2.8 2.2 3 16 4 3 15 b uluruz. 78
f(x) x.f ‘(x) dx 6x c eşitliği veriliyor. f(1) 5 olduğuna göre, f( 1) kaçtır? A) 3 B) 4 C) 5 D) 6 E ) 7 Sabit terim x.f(x) ‘in türevi 1.f(x) x.f ‘(x) tir. O halde; f(x) x.f ‘(x) dx x.f(x) d dir. (c : Çözüm 1 dir. 1 yazmadık Sorudaki c ile karışmasın diye) x.f(x) d 6x c ise xf(x) 6x c d x 1 olduğunda; 1.f(1) 6 c d 5 6 c d x 1 olduğunda; 1.f( 1) 6 c d f( 1) 7 f( 1) 7 buluruz. www.matematikkolay.net 98
www.matematikkolay.net 2 2 f(x) fonksiyonu için, d f(x) 2x 1 olup f(x)’in eğrisi x 1 noktasında dx x eksenine teğet ise f( 1) in değeri kaçtır? 1 1 5 7 10 A) B) C) D) E) 3 3 3 3 3 f ‘ 1 0 dır. x 1 de teğetin eğimi 0 olduğundan f 1 0 dır. x 1 için y 0 olduğu için x : f ” x 2 Çözüm 2 2 2 3 2 1 ise 1 basamak integral alalım. f ‘ x x x c dir. f ‘ 1 0 idi. 0 1 1 c c 2 dir. O halde; f ‘ x x x 2 dir. 1 basamak integral alalım. x x f x 2x d dir. f 1 0 idi. 3 2 1 1 0 2 d d 3 2 3 2 7 dır. 6 x x 7 f x 2x ise 3 2 6 1 1 7 10 f 1 2 buluruz. 3 2 6 3 141
Aşağıda, bir f fonksiyonunun türevinin grafiği verilmiştir. f(0) 1 olduğuna göre, f(2) değeri kaçtır? 3 5 4 1 1 A) B) C) D) E) 2 2 3 2 3 www.matematikkolay.net 2 1 2 Grafik; x , x 1 f ‘(x) 1 , x 1 İntegral alalım, x c , x 1 f(x) 2 x c , x : Çözüm 2 1 1 2 2 1 2 2 1 0 f(0) 1 ise 1 c c 1 dır. 2 Türev için fonksiyon sürekli olmalıdır. Bunun için x 1 noktasında parçalı fonksiyonlar aynı değeri vermelidir. x 1 3 f(1) c 1 2 2 2 3 3 f(1) x c 1 c c 2 2 2 2 1 2 Buna göre; 1 5 f(2) x c 2 buluruz. 2 2 www.matematikkolay.net 146
f fonksiyonunun birinci türevi 1 x 0 f ‘(x) x 1 0 x 1 2 x 1 biçiminde tanımlanıyor. 1 f(0) olduğuna göre, f(2) f( 1) toplamı kaçtır? 2 11 7 5 1 3 A) B) C) D) E) 2 2 2 2 2 1 2 2 Bölge bölge integral alalım. x C x 0 x f(x) x C 0 x 1 2 2 : Çözüm 3 1 2 2 3 x C x 1 Sınır değerlerde fonksiyon eşit olmalıdır.(süreklilik) 1 1 1 f(0) ise C ve C dir. 2 2 2 x 1 1 1 f(1) x 1 2 dir. 2 2 2 2 f(1) 2 C 0 dır. Buna göre; f(2) 2x 2.2 4 f 1 1 ( 1) x dir. 2 2 1 7 Toplamları: f(2) f( 1) 4 buluruz. 2 2
2 2 2 dy 2y x y dx olduğuna göre, y f(x) fonksiyonu aşağıdakilerden hangisidir? 1 1 A) B) x c x c C) 2 2 2 1 1 D) x 2x c x x c 1 E) x x c 2 2 2 2 2 2 y’ 2y x y y’ y 2x 1 y’ 2x 1 iki tarafın da integralini alalım. y 1 x x y 1 x x c : y Çözüm 2 şeklinde yazabiliriz. 1 y buluruz. x x c www.matematikkolay.net 106
2 a 0 olmak üzere, a 1 dx fonksiyonu veriliyor. x (a 1).x a 1 f 3 f olduğuna göre, a kaçtır 3 ? 1 1 A) 4 B) 2 C) 1 D) E) 2 4 2 a 1 a 1 dx dx x (a 1).x a (x a)(x 1) 1 1 dx ln|x a| ln|x 1| x a x 1 x a ln c dir. x 1 1 f(3) f( ) 3 : Çözüm 1 a 3 a ln c ln 3 c 3 1 1 1 3 1 a 3 a 3 3 1 1 1 3 3:00 AM 4 1 3a 3 4 3 3 a 1 3a 3 a 1 3a a 1 (a 0 idi.) 3 a 3a 1 4a 4a a 1 buluruz. www.matematikkolay.net 22
2 2x.f(x) f ‘(x) x .f ‘(x) f(2) 12 olduğuna göre, f(3) kaçtır? A) 28 B) 30 C) 32 D) 34 E) 36 www.matematikkolay.net 2 2 2 2 2xf(x) f ‘(x) x .f ‘(x) 2xf(x) f ‘(x)(x 1) f(x) x 1 f ‘(x) 2x (İ f ‘(x) 2x f(x) : x 1 Çözüm 2 2 ln(x 1) C 2 C C C C ntegral alalım) lnf(x) ln(x 1) C f(x) e (x 1).e dir. x 2 için f(2) (4 1).e 12 e 4 x 3 için f(3) (9 1).e 8.4 32 buluruz. 26
2 2 f ‘(x) 0, f(0) f ‘(0) ve f ”(x) f ‘(x) e olduğuna göre, f( 1) kaçtır? A) e B) e C) 0 D) e E) e 2 www.matematikkolay.net 2 f ”(x) f ‘(x) e iki tarafın da türevini alalım. f ”'(x) f ”(x) 0 f ”'(x) f ”(x) : f ”'( Çözüm x C x C 2 C c 2 2 x C c x) 1 iki tarafın da integralini alalım. f ”(x) lnf ”(x) x C f ”(x) e tekrar integral alalım. f ‘(x) e C x 0 için e C 0 C e dir. f ‘(x) e e tekrar inte x C c 3 C C 3 3 x C c C 2 x C x C c 2 c 2 x 2 2 2 2 2 gral alalım. f(x) e e x C x 0 için e C 0 C e f(x) e e x e olur. f ”(x) f ‘(x) e idi. e (e e ) e e e c 2 dir. f(x) e e x e dir. f( 1) e e e e buluruz . 27
www.matematikkolay.net x x e .f(x)dx e .cosx c olduğuna göre, f(x) fonksiyonunun y eksenini kes – tiği nok tanın ordi natı kaçtır? A) 2e B) e C) 1 D) 1 E) 2 x x x x x e .f(x)dx e .cosx C iki tarafın türevi alalım. e .f(x) e .cosx e .sinx x 0 için : Çözüm 0 0 0 e .f(0) e .cos0 e .sin0 f(0) 1 buluruz. 29
2 f(sinx)cosxdx F(x) olduğuna göre, f(sin x).sinx.cos x.dx işleminin sonucunun F(x) türün den eşiti nedir? F(x) F(x) A) F(x) B) C) D) F(x) E) 2F(x) 4 2 2 f(sinx)cosxdx F(x) u sinx du cosxdx f(sinx).cosx.dx f(u)du F(x) ise; f(sin x). : si Çözüm 2 2 nx.cosx.dx u sin x du sinxcosxdx 1 F(x) f(sin x).sinx.cosx.dx f(u).du buluruz. 2 2 48
f(x).cosxdx f(x).sinx cosx c olduğuna göre, f(x) aşağıdakilerden hangisidir? A) sinx c B) 2 cosx c C) x c D) x c E) 2x c f(x).cosxdx f(x).sinx cosx c Direkt iki tarafın türevini alarak çözebiliriz f(x).cosx : Çözüm f ‘(x)sinx f(x).cosx sinx f ‘(x)sinx sinx f ‘(x) sinx sinx f ‘(x) 1 İki tarafın da integralini alalım. f(x) x c buluruz. www.matematikkolay.net 64
f ‘(x) cosx sinx ve f 2 ise f ? 2 4 www.matematikkolay.net f(x) f ‘(x) dx cosx sinx dx sinx cosx c f(x) sinx cosx c dir. x için : f(x) 2 ise 2 sin 2 Çözüm cos c 2 2 1 0 c 2 c 1 dir. O halde; f(x) sinx cosx 1 dir. Buna göre; 2 f sin cos 1 4 4 4 2 2 2 1 1 buluruz. 67
cosx c f( x)dx ise f(x) ? cotx c f(x)dx cosx c f(x)dx İki tarafın da türevini alalım. sinx cosx ‘sinx sinx ‘ : cos Çözüm 2 2 2 2 2 2 2 2 2 2 2 x f(x) sin x sinx.sinx cosxcosx f(x sin x sin x cos x f(x) sin x sin x cos x f(x) (Not : sin x cos x 1 dir) sin x 1 f(x) buluruz. sin x www.matematikkolay.net 72
x 2 f(x) 2 sinx 2cos x dx ise f ‘(0) ? x 2 f ‘(x) x 2 0 2 f(x) 2 sinx 2cos x dx ise; f ‘(x) 2 sinx 2cos x tir. f ‘(0) 2 sin0 2 : cos Çözüm 0 1 0 2 1 buluruz. 75
www.matematikkolay.net x 3x 1 2 3 e .f(x)dx e c 1 olduğuna göre, f ‘ değeri kaçtır? 2 A) 3 B) 6 C) 6e D) 6e E) 6e x 3x 1 ı ı x 3x 1 x e .f(x)dx e c Eşitliğin iki tarafının da türevini alalım. e .f(x)dx e : c e . Çözüm 3x 1 3x 1 2x 1 x ı 2x 1 1 02.Oca ı 2 1 1 0 1 3e f(x) 3.e f(x) 3e dir. e f (x) 6e dir. 1 f 6e 6e 6e 6 bulunur. 2 83

