Soru Sor sayfası kullanılarak Türevin Anlamı konusu altında İki değişkenli fonksiyonda teğetin eğimi ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
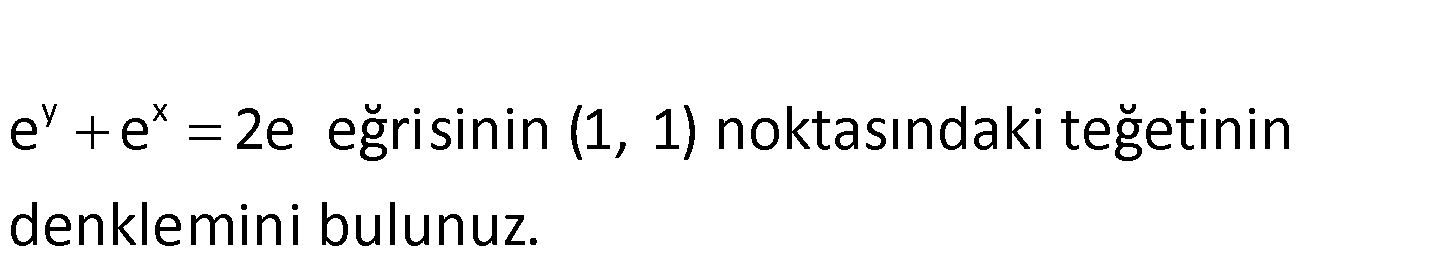

2.SORU


3.SORU
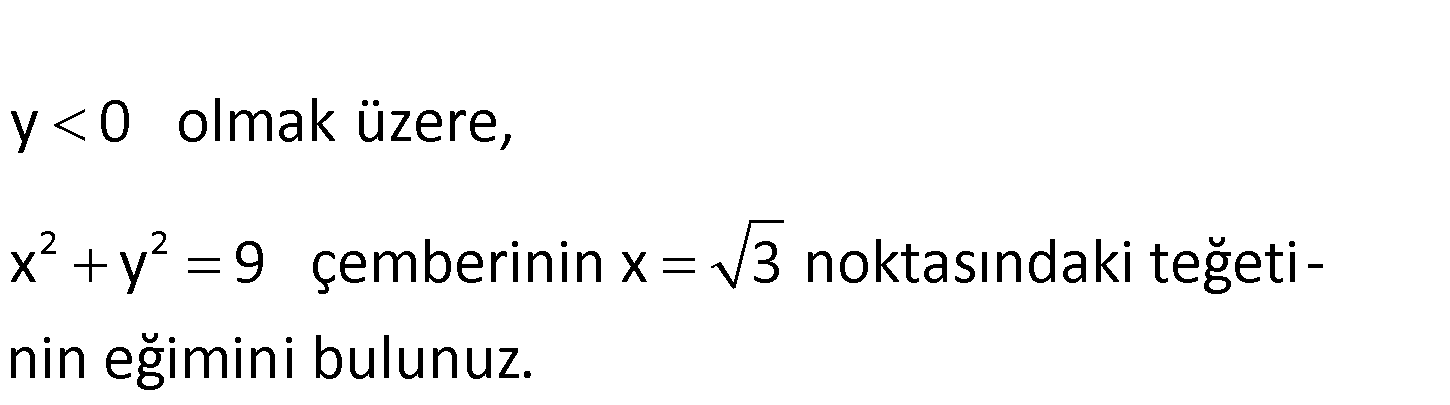

4.SORU

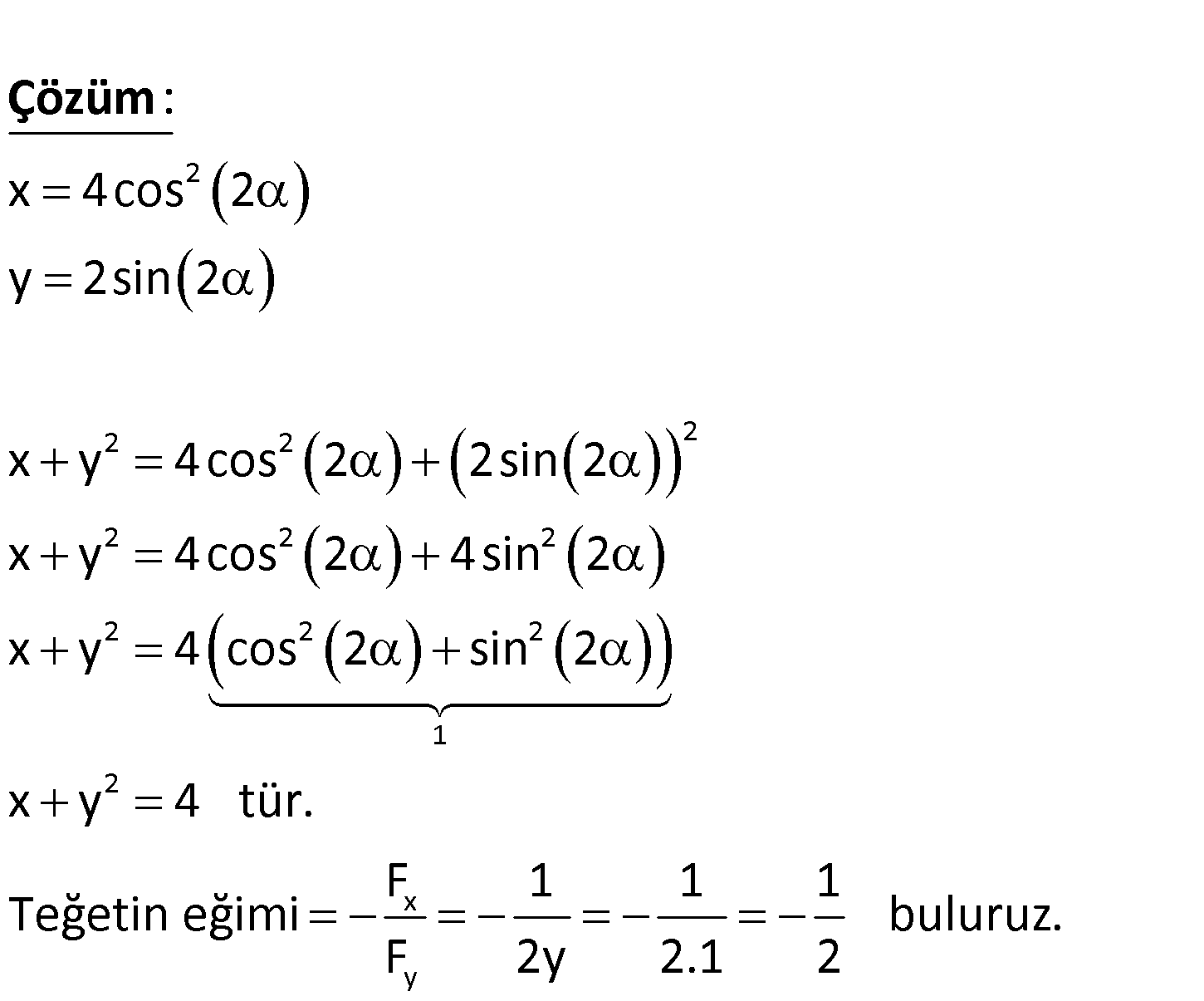
5.SORU

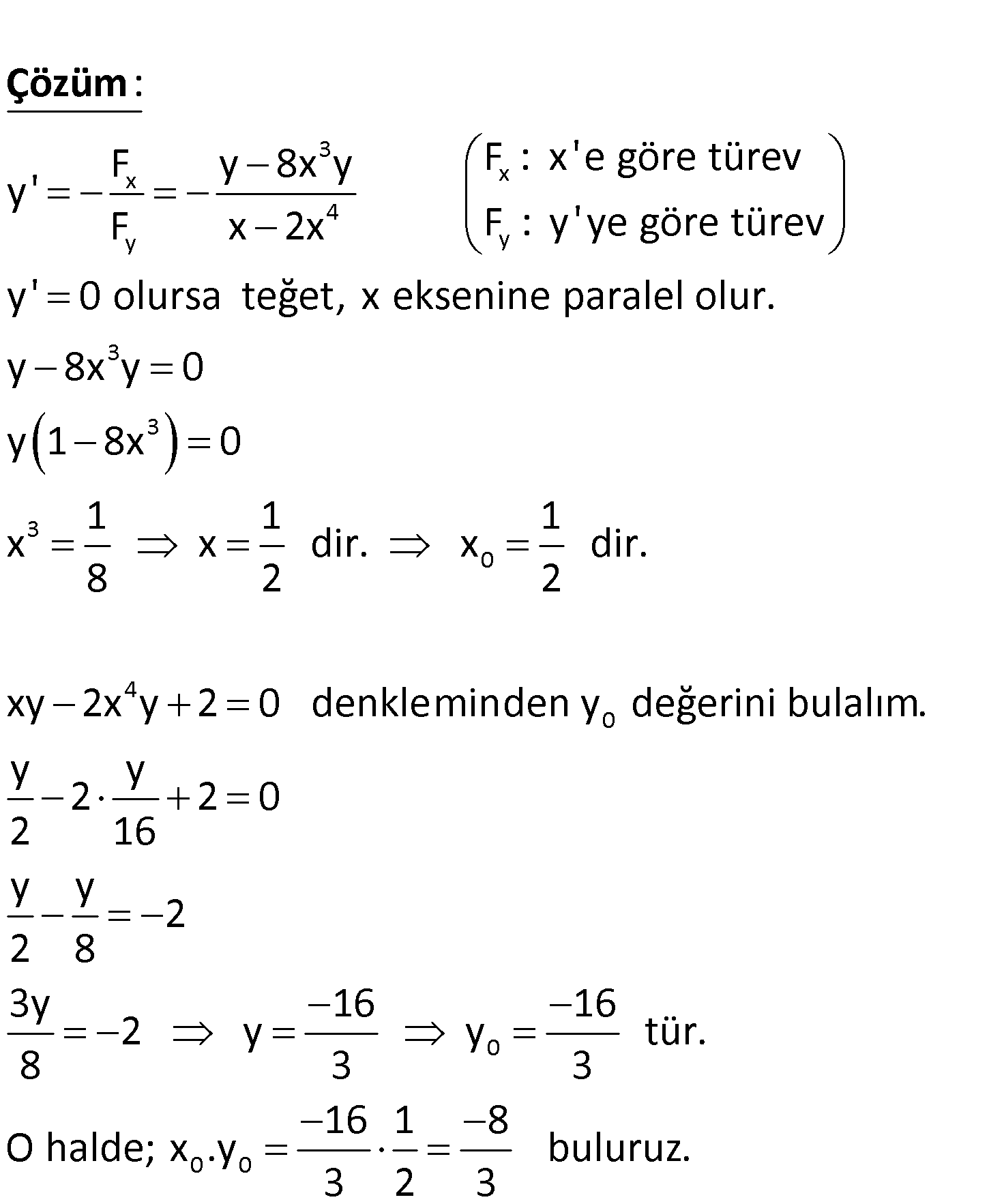
Diğer Soru Tipleri için Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
www.matematikkolay.net y x e e 2e eğrisinin (1, 1) noktasındaki teğetinin denklemini bulunuz. y x x 1 x y 1 y e e 2e 0 Teğetin eğimi; F e e 1 buluruz. F e e (1,1) noktasından geçen ve eğimi 1 : Çözüm olan doğru; y 1 1(x 1) y 1 x 1 x y 2 0 buluruz. 76
2 2 (x 2) (y 3) 2 çemberine üzerindeki A(3, 2) noktasından çizilen normalin denklemini bulunuz. 2 2 x y (x 2) (y 3) 2 0 Teğetin eğimi; F 2(x 2) 2(3 2) 2 1 buluruz. F 2(y 3) 2(2 3) 2 normalin e : Çözüm N N T N N ğimi ise m ; m .m 1 m .1 1 m 1 dir. (3,2) noktasından geçen ve eğimi 1 olan doğru; y 2 1(x 3) y 2 x 3 x y 5 0 buluruz. 77
2 2 y 0 olmak üzere, x y 9 çemberinin x 3 noktasındaki teğeti – nin eğimini bulunuz. www.matematikkolay.net 2 2 2 2 x y x 3 için y’nin değerini bulalım. x y 9 3 y 9 y 6 y 0 dendiği için y 6 dır. F m F : Çözüm 2x x 3 1 2 buluruz. 2y y 6 2 2 86
2 x 4cos (2 ) y 2sin(2 ) Denklemleriyle verilen f(x) fonksiyonunun y 1 ordinatlı noktasındaki teğe n ti in eğimi nedir? 2 2 2 2 2 2 2 2 2 2 1 2 x 4cos 2 y 2sin 2 x y 4cos 2 2sin 2 x y 4cos : 2 4sin 2 x y 4 cos 2 sin 2 x y 4 Çözüm x y tür. F 1 1 1 Teğetin eğimi buluruz. F 2y 2.1 2 www.matematikkolay.net 123
www.matematikkolay.net 4 0 0 Analitik düzlemde xy 2x y 2 0 denklemiyle verilen y f(x) fonksiyonuna üzerinde – ki A(x , y ) no 0 0 ktasından çizilen teğet doğrusu x eksenine paralel olduğuna göre, x .y çarpımı kaç – tır? 8 4 1 1 1 A) B) C) D) E) 3 3 2 4 6 3 x x 4 y y F y 8x y F : x’e göre türev y’ F x 2x F : y’ye göre türev y’ 0 olursa t : eğet Çözüm 3 3 3 0 4 0 0 0 0 , x eksenine paralel olur. y 8x y 0 y 1 8x 0 1 1 1 x x dir. x dir. 8 2 2 xy 2x y 2 0 denkleminden y değerini bulalım. y y 2 2 0 2 16 y y 2 2 8 3y 16 16 2 y y tür. 8 3 3 16 1 8 O halde; x .y 3 2 buluruz. 3 140

