Soru Sor sayfası kullanılarak Türevin Anlamı konusu altında Yatay Asimptot, Düşey Asimptot, Asimptotların Kesim Noktası ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
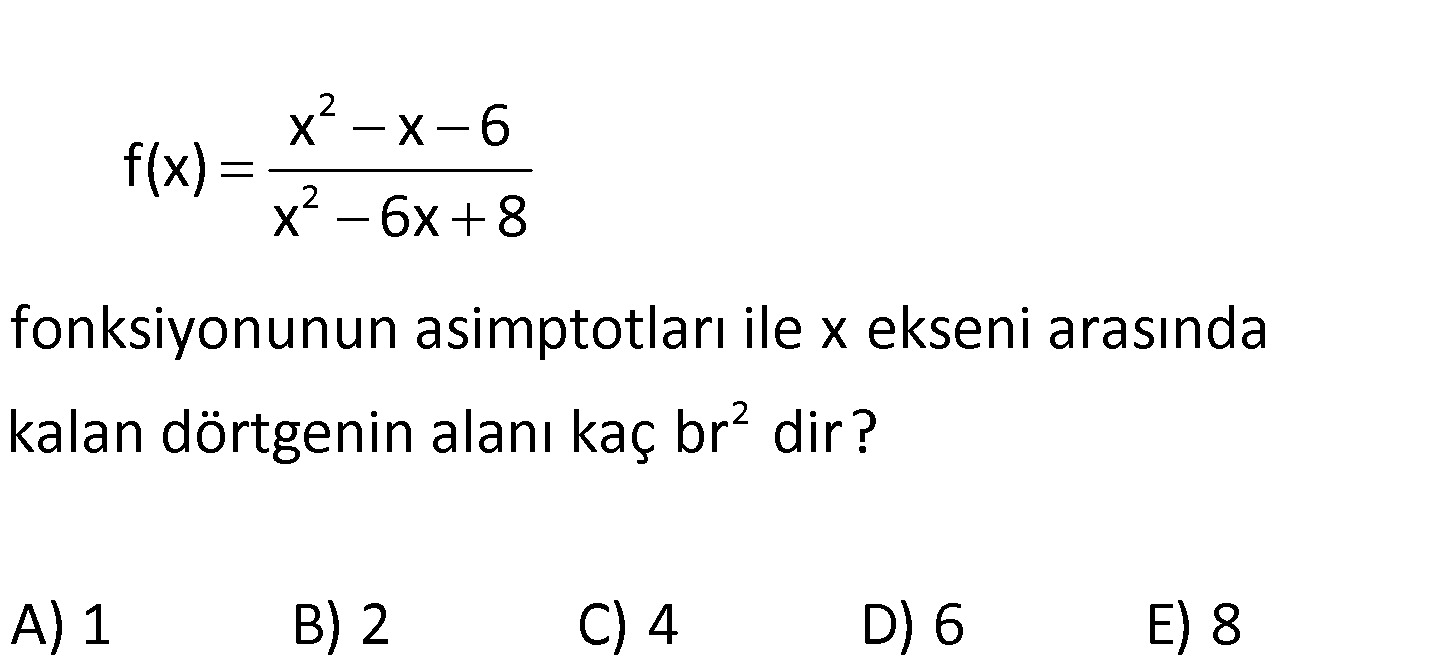

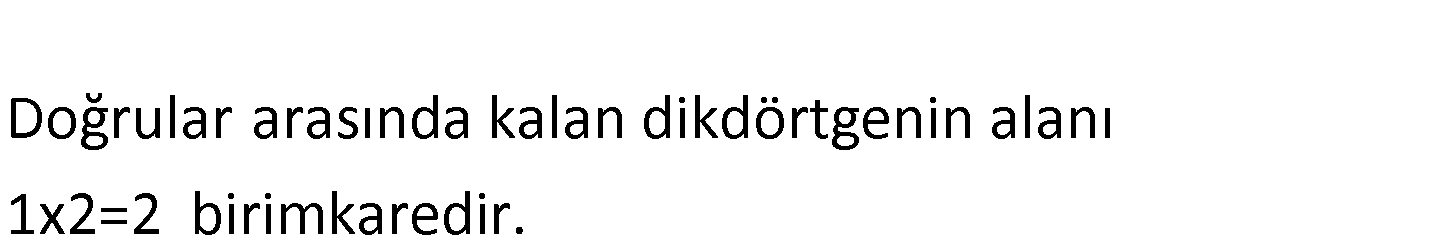
2.SORU


3.SORU
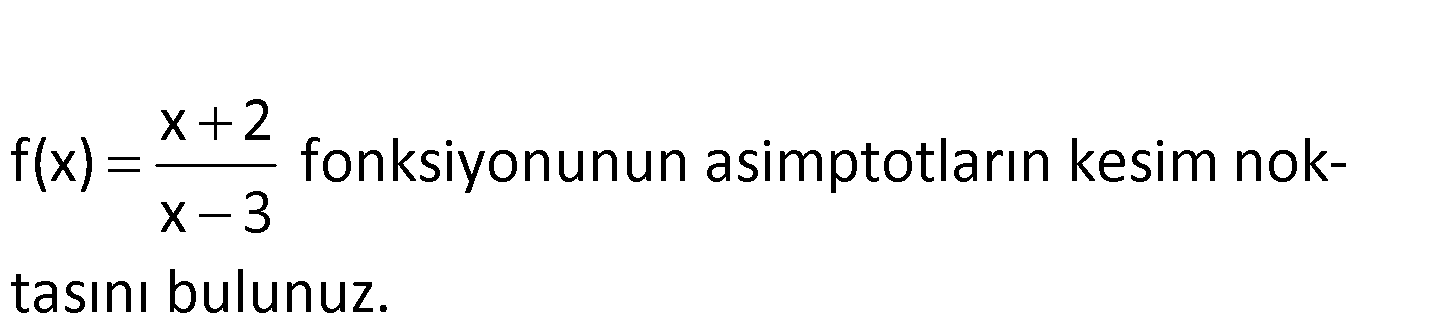

4.SORU


5.SORU


6.SORU


7.SORU


8.SORU


9.SORU


10.SORU
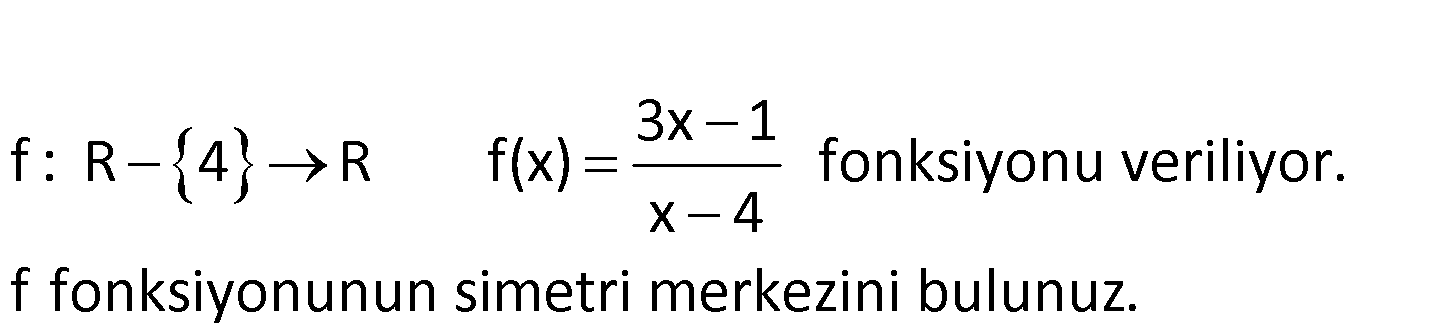

11.SORU
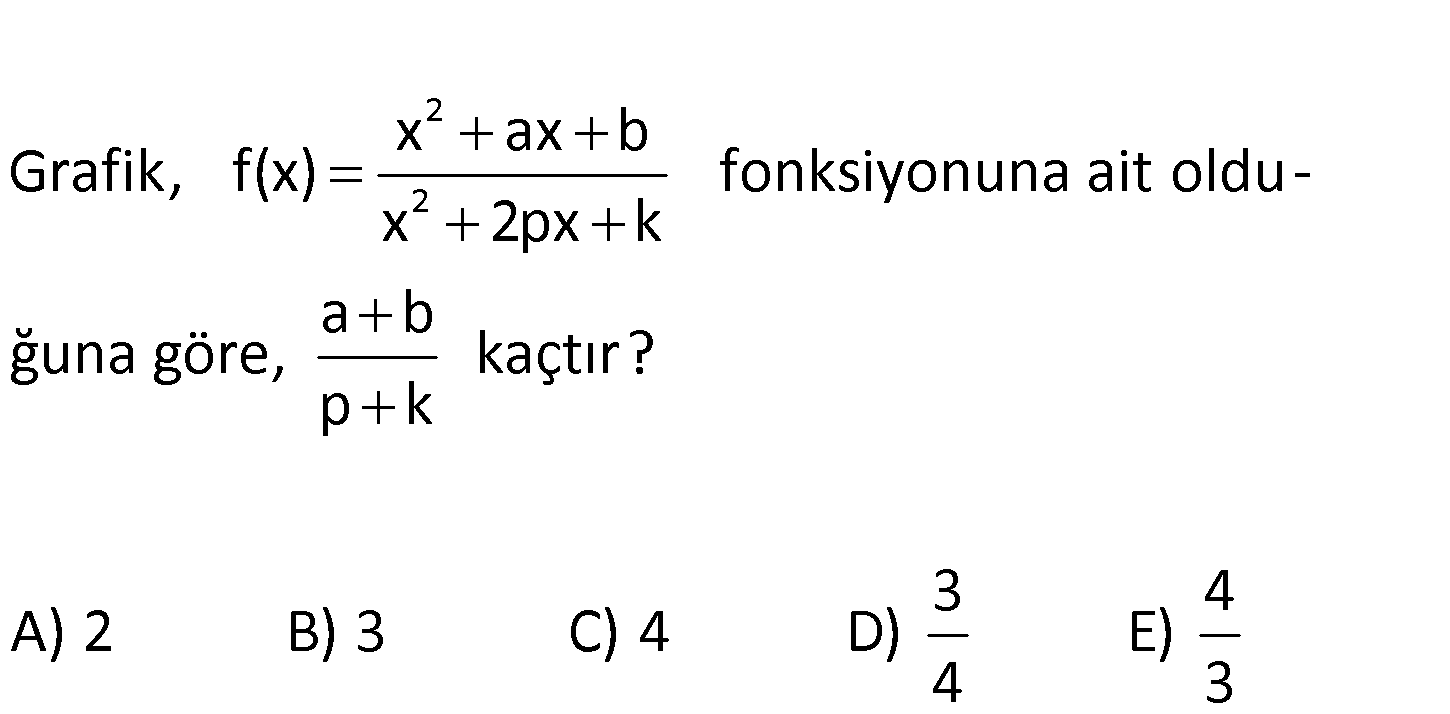

12.SORU
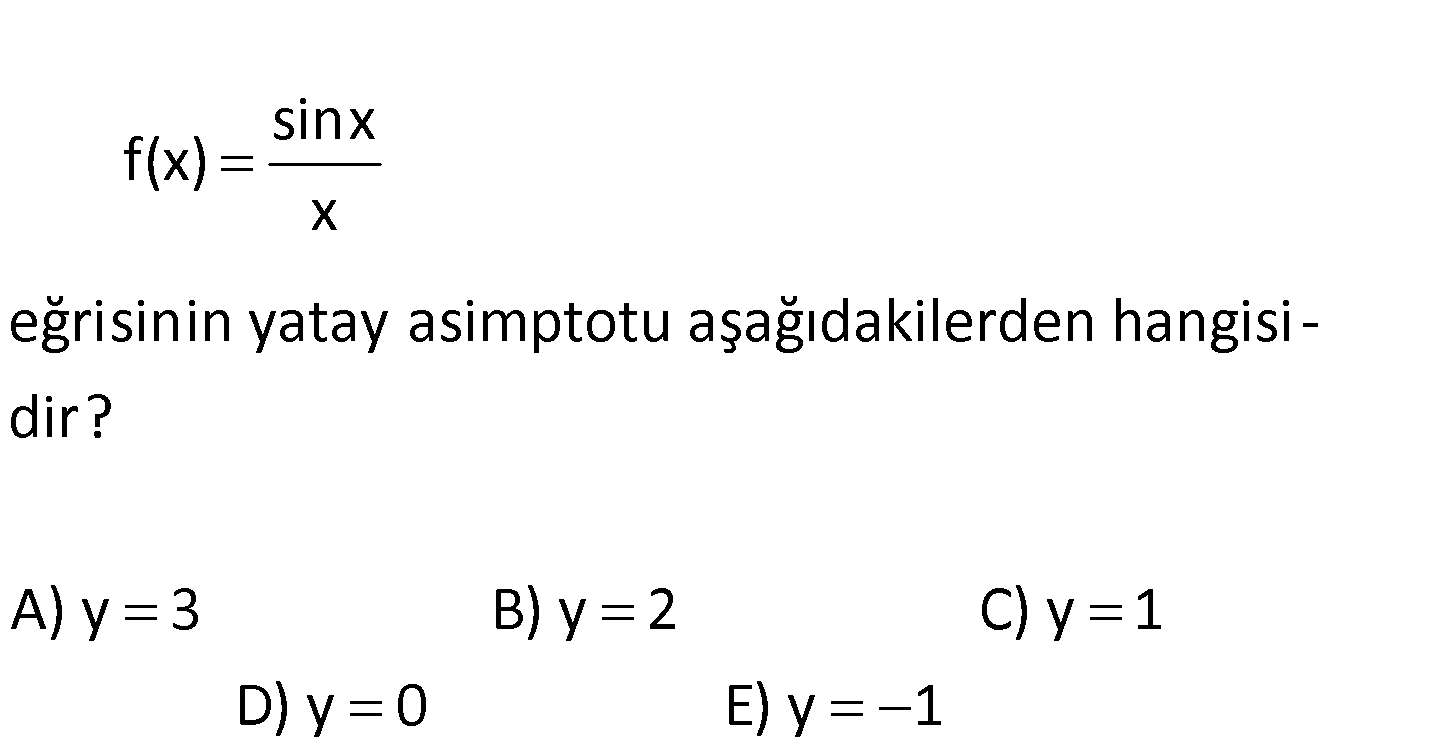

13.SORU


Diğer Soru Tipleri için Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
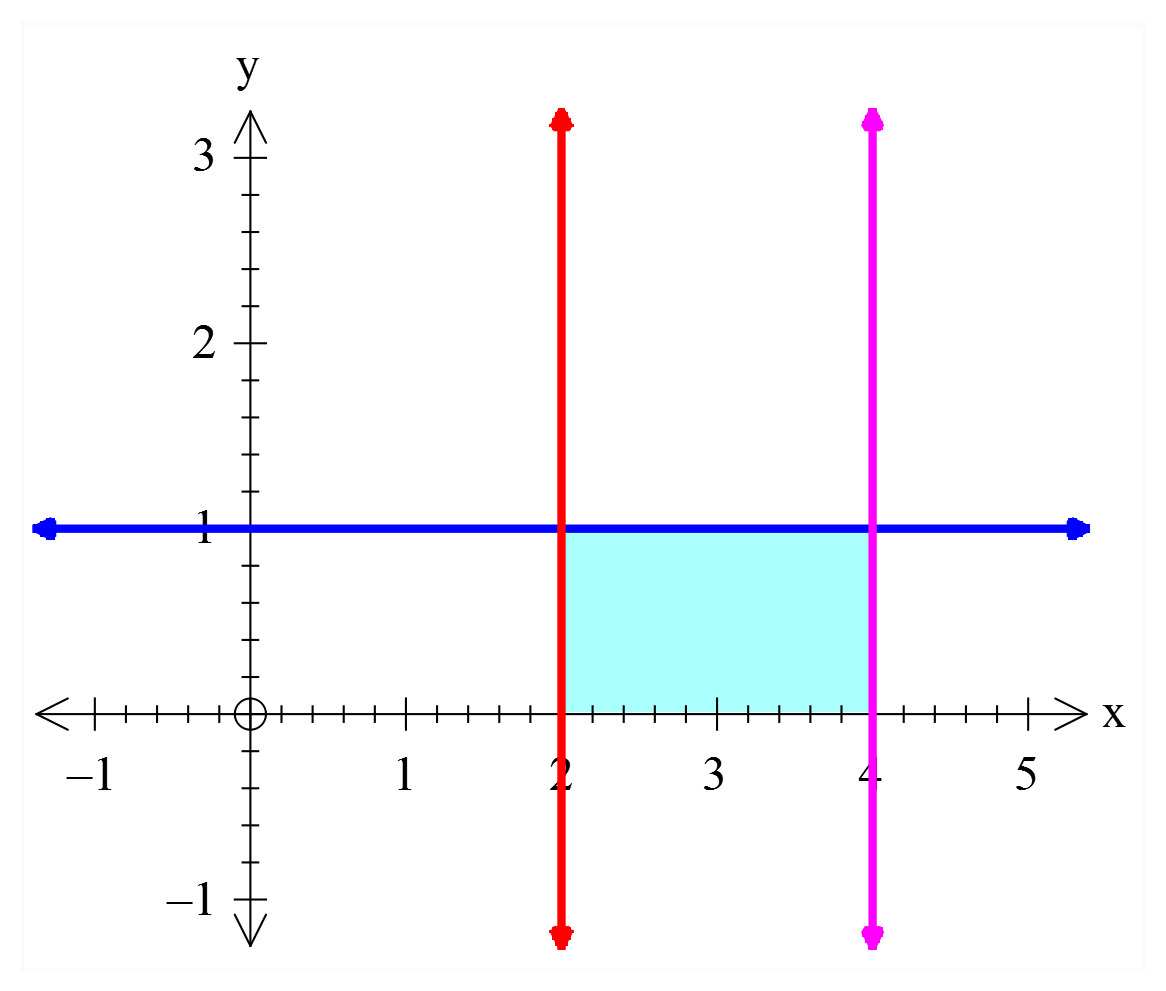
2 2 x x 6 f(x) x 6x 8 fonksiyonunun asimptotları ile x ekseni arasında kalan dörtgenin alanı k 2 aç br dir? A) 1 B) 2 C) 4 D) 6 E) 8 www.matematikkolay.net 2 2 2 x x 2 : x x 6 f(x) x 6x 8 Yatay asimptot x x 6 lim f(x) lim 1 y 1 doğrusu x 6x 8 Düşey asim Çözüm 2 ptotlar Paydayı 0 yapan x değerleridir. x 6x 8 0 (x 2)(x 4) 0 x 2 ve x 4 doğrularıdır. Doğrular arasında kalan dikdörtgenin alanı 1×2=2 birimkaredir. 5
2 3x g(x) fonksiy onunun yatay asi mptotu n edir? x 2 www.matematikkolay.net x x 2 x 2 : Yatay asimptot 3x lim f(x) lim belirsizliği var. Türev alalım. x 2 3x lim x l 2 Çözüm x 3 im 0 buluruz. 2x Buna göre yatay asimptot : y 0 doğrusudur. 13
x 2 f(x) fonksiyonunun asimptotların kes im no kx 3 tasını bul u u n z. www.matematikkolay.net x x : x 2 f(x) x 3 Yatay asimptot x 2 lim f(x) lim 1 y 1 doğrusudur. x 3 Düşey asimpto t Payday Çözüm ı 0 yapan x değeridir. x 3 0 x 3 doğrusudur. Bu iki doğrunun kesim noktasını (3,1) noktası buluruz. 17
www.matematikkolay.net 2 2 ax b f(x) x cx 16 eğrisinin asimptotları sadece bir noktada kesişmek – tedir. a c 10 oldu ğuna göre, a nın alabileceği değerler çarpımı kaçtır? A) 12 B) 16 C) 24 D) 36 E) 42 Bir tane yatay asimptotu, bir tane de düşey asimptotu olmalıdır. Düşey asimptotun bir t : ane o Çözüm 2 2 8 18 8 lması için, Paydayı 0 yapan tek bir x değeri olmalıdır. Yani payda tam kare olmalıdır. x cx 16 Bu da ancak c 8 veya c 8 iken mümkündür. 0 ı kullanarak da c değerlerini bulabiliriz. a c 10 a 2 veya 18 dir. a’nın değerleri çarpımı 2.18 36 buluruz. 65
www.matematikkolay.net 2 2 3x 12 f(x) x x eğrisinin asimptotlarından biri eğriyi A noktasında kesiyor. Buna göre, A nokta sının orjine uzaklığı kaç birim – dir? A) 7 B) 6 C) 5 D) 5 E) 3 2 x 2 2 3x 12 lim 3 (y 3 yatay asimptot) x x y 3 asimtotu ile f(x) eğrisini ortak çözelim. 3x 1 x : 2 Çözüm 2 2 3 3x x 2 12 3x 2 2 3x x 4 noktasında kesişirler. ( 4,3) noktasının orjine uzaklığı; ( 4) 3 5 br bulunur. 100
4x 3 f(x) fonksiyonunun grafiği ile bu fonksiyo – x 2 nun yatay asimptotu, (a, b) noktasında kesişi yor. Buna göre, a b toplamı kaçtır? 47 23 45 11 43 A) B) C) D) E) 8 4 8 2 8 www.matematikkolay.net x 4x 3 limf(x) 4 tür. y 4 (yatay asimptot) x 2 y 4 doğrusu ile kesişen x noktasını bula : Çözüm lım. 4x 3 4 pay ve payda zıt işaretli olmalı ki x 2 bir x değeri bulunabilsin. 4x 3 4 4x 3 8 4x 8x 11 2 x 11 x 8 11 43 Buna göre, a b 4 buluruz. 8 8 108
4 2 2 f(x) x 6x ax b fonksiyonunun yatay asimptotu Ox eksenidir. a ve b birer gerçel sayı olduğ una göre, a b kaçtır? A) 6 B) 3 C) 3 D) 6 E) 9 www.matematikkolay.net x 4 2 2 x 4 2 2 x x x O ekseni y 0 doğrusudur. lim x 6x ax b 0 olmalıdır. lim x 6x lim a : x b 0 lim Çözüm 4 2 2 x 2 2 2 2 x x 2 2 2 x 2 x 6x lim ax b lim (x 3) 6x lim ax b (x 3) 6x lim 1 ax b a 1 ve b 3 olmalıdır. a.b 1.( 3) 3 buluruz. 109
2 2 3x 12 f(x) x x eğrisinin asimptotlarından biri eğriyi A noktasında kesiyor. Buna göre, A noktasının orjine uzaklığı kaç birim – dir? A) 7 B) 6 C) 5 D) 4 E) 3 2 x 2 Yatay asimptotu bulalım. 3x 12 lim 3 tür. y 3 asimptotu x x Bu eğri , 3 değ : erini başka Çözüm 2 2 2 bir noktada veriyorsa bu noktayı bulalım. 3x 12 3 x x 3x 2 12 3x 2 2 3x 12 3x x 4 buluruz. Demek ki y 3 asimptotu bu eğriyi ( 4,3) noktasında kesiyor. Orjine uzaklığı ( 4) 3 5 tir. www.matematikkolay.net 115
: 5x 2 fonksiyonunun yatay ve düşey as imptot ları – x 6 nı bulu nuz. x x x – x : Yatay asimptotlara bakalım. 5x 2 5x 2 lim lim 5 y 5 x 6 x 6 5x 2 5 lim lim x 6 Çözüm x 2 5 tir. y 5 x 6 Düşey asimptotlara bakalım; 5x 2 x 6 ve x 6 asimptotlarıdır. x 6 Paydayı 0 yapan değerler 118
3x 1 f : R 4 R f(x) fonksiyonu veriliyor. x 4 f fonksiyonunun simetri merkezini bulunuz. 3x 1 fonksiyonunun simetri merkezi asipmtotların x 4 kesişim noktasıdır. Düşey asimpto : t, payd Çözüm x ayı 0 yapan x değeridir. x 4 0 x 4 tür. Yatay asimptot, x için limitidir. 3x 1 lim 3 tür. y 3 yatay asimptottur. x 4 Bu iki asimptot 4,3 noktasında kesişirler. Buna göre; Simetri merkezi 4,3 noktasıdır. 134
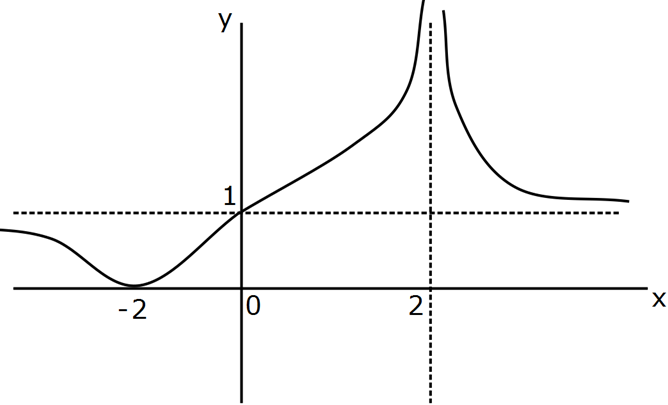
www.matematikkolay.net 2 2 x ax b Grafik, f(x) fonksiyonuna ait oldux 2px k a b ğuna göre, kaçtır? p k 3 A) 2 B) 3 C) 4 D) 4 4 E) 3 www.matematikkolay.net x 2 noktasında düşey asimptot var. Demek ki x 2 için fonksiyonun paydası 0 oluyor. Ayrıca : x 2 Çözüm 2 2 değeri, çift katlı kök olmalıdır. Çünkü f(x), x 2’den önce ve sonra pozitiftir. İşaret değiş – tirmemiştir. O halde; payda x 2 x 4x 4 tür. Buna göre; p 2 , k 4 olmalıdır. x 0 için f(x) 1 ise grafi 2 2 2 kten görüyoruz. x ax b b 1 1 b k dir. x 2px k k b 4 tür. x 2 için f(x) 0 ise grafikten görüyoruz. x 2 için kesrin payı 0 dır. x ax b 4 0 4 2a b 0 4 b 2a a 4 tür. O halde; a b 4 4 8 4 buluruz. p k 2 4 2 143
sinx f(x) x eğrisinin yatay asimptotu aşağıdakilerden hangisi – dir? A) y 3 B) y 2 C) y 1 D) y 0 E) y 1 www.matematikkolay.net x Yatay asimptot için x ‘da limit değerine bakılır. sinx lim x sinx en fazla 1 veya 1 : ola Çözüm x x 0 bilirken yani sınırlı iken paydadaki x, sonsuza gidiyor. Sayı 0 olduğundan bu limit değeri de 0’a eşittir. sonsuz sinx lim 0 buluruz. Cevap: y 0 x sinx Not : x 0’a giderken lim 1 ‘e eşittir. x 146
2 2 ax 4 y x bx c fonksiyonuna ait asimptotların denklemleri x 1, x 2 ve y 2 doğruları olduğun a göre, a b c kaçtır? A) 3 B) 2 C) 1 D) 2 E) 7 www.matematikkolay.net 2 2 ax 4 y x bx c Düşey asimptotlar, paydayı 0 yapan x değerleridir. Düşey asimptotlar, x 1 v : e Çözüm 2 b c 2 2 2 x 2 x 2 ise payda x 1 x 2 x 3x 2 dir. ax 4 y olur. x 3x 2 Yatay asimptot ise sonsuzdaki limit değeridir. ax 4 a lim a dır. y a doğrusudur. x 3x 2 1 Buna göre; a 2 dir. O halde; a b c 2 3 2 52 7 buluruz. 147

