Soru Sor sayfası kullanılarak Türevin Anlamı konusu altında En Kısa Mesafe, En Kısa Uzunluk, En Kısa Yol Soruları ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU


2.SORU


3.SORU


4.SORU


5.SORU


6.SORU

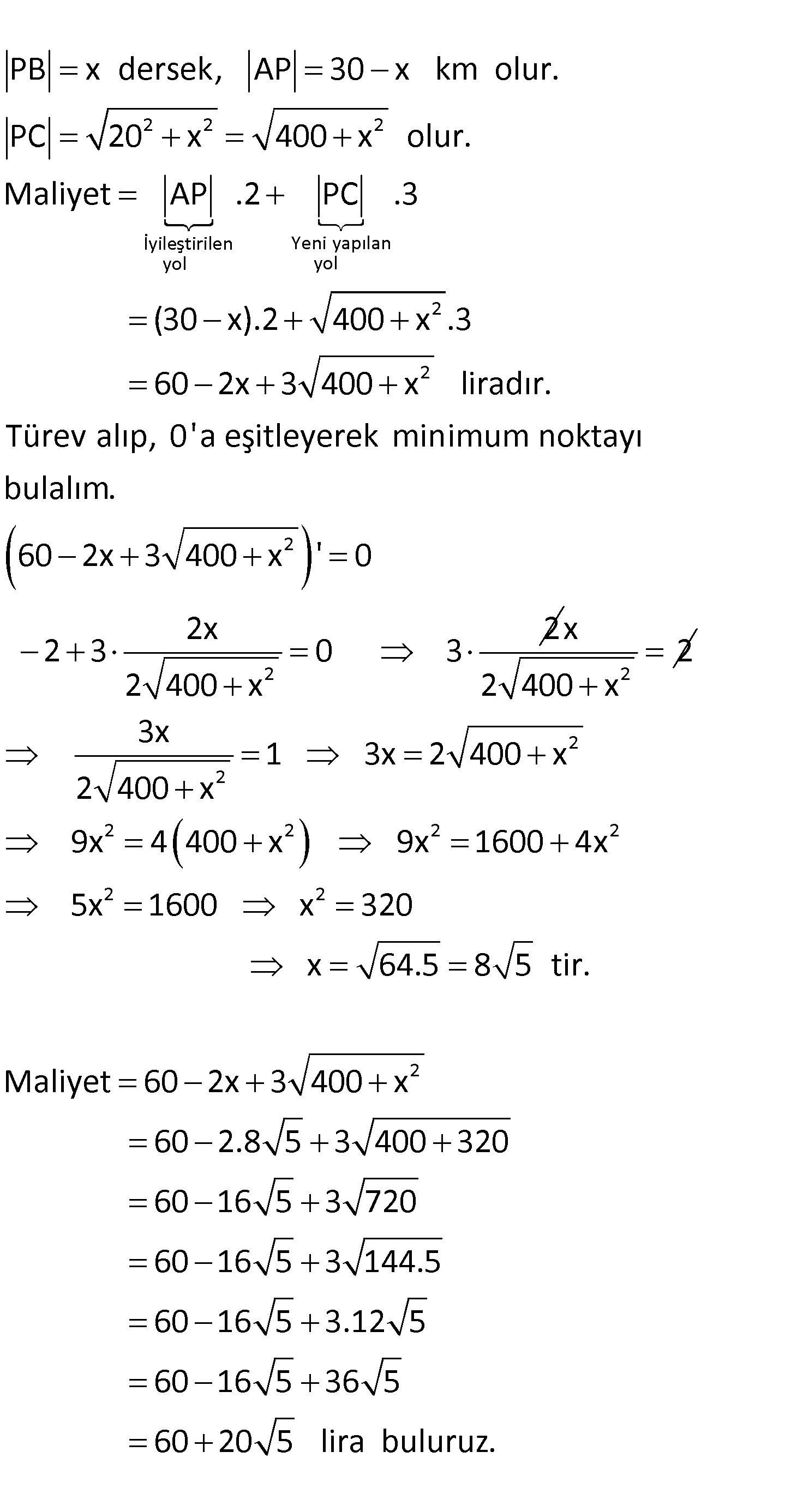
7.SORU

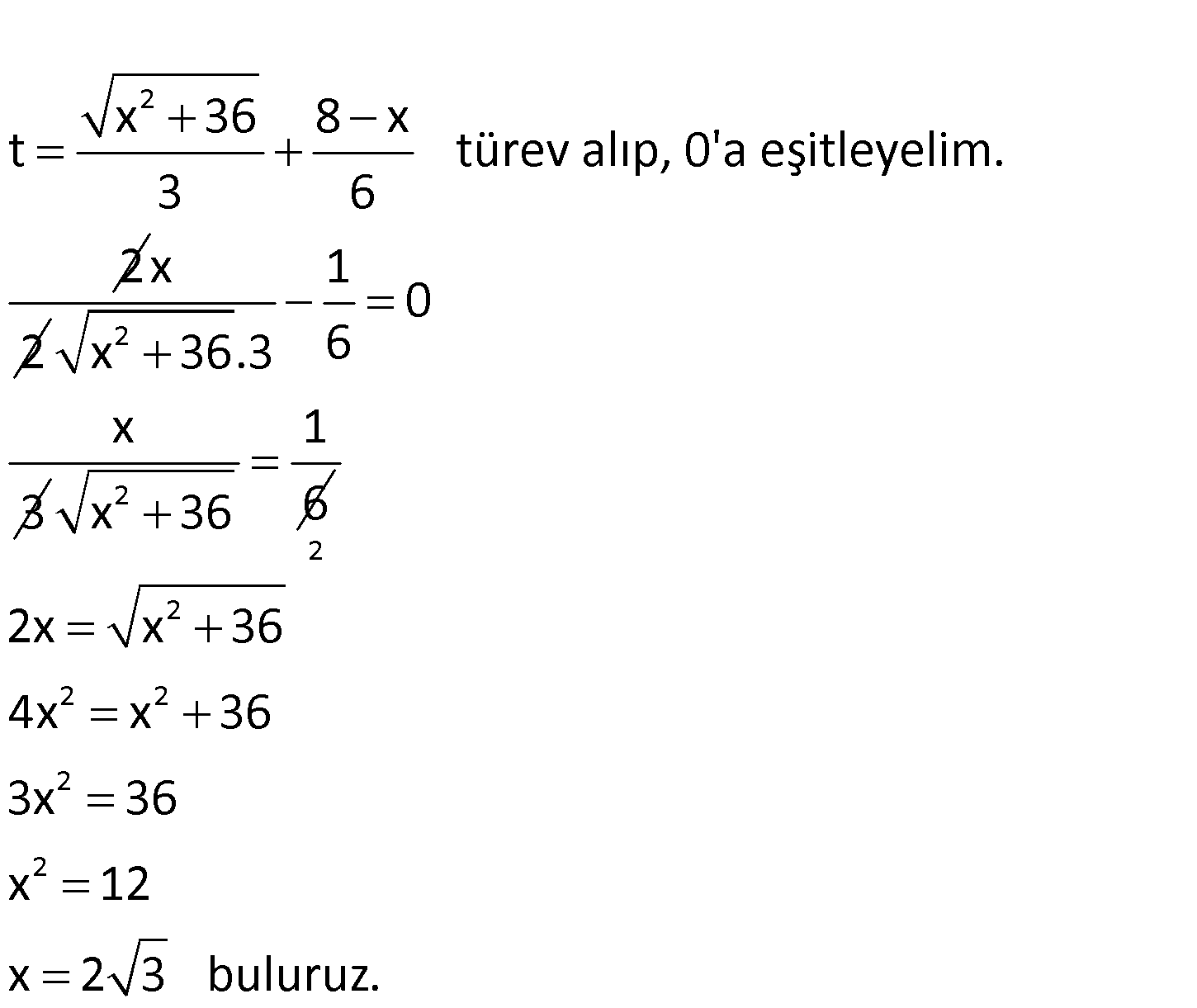
8.SORU

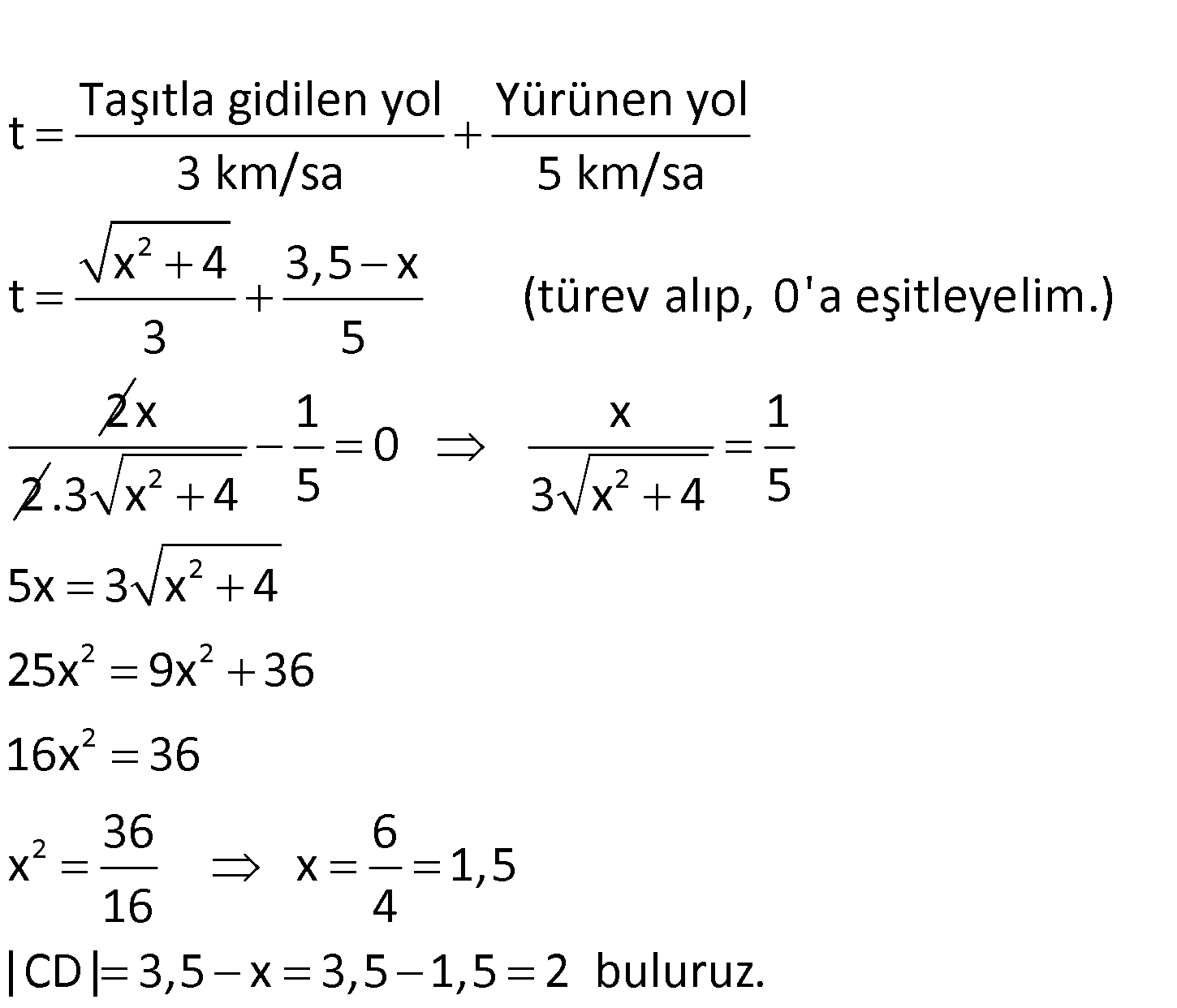
9.SORU

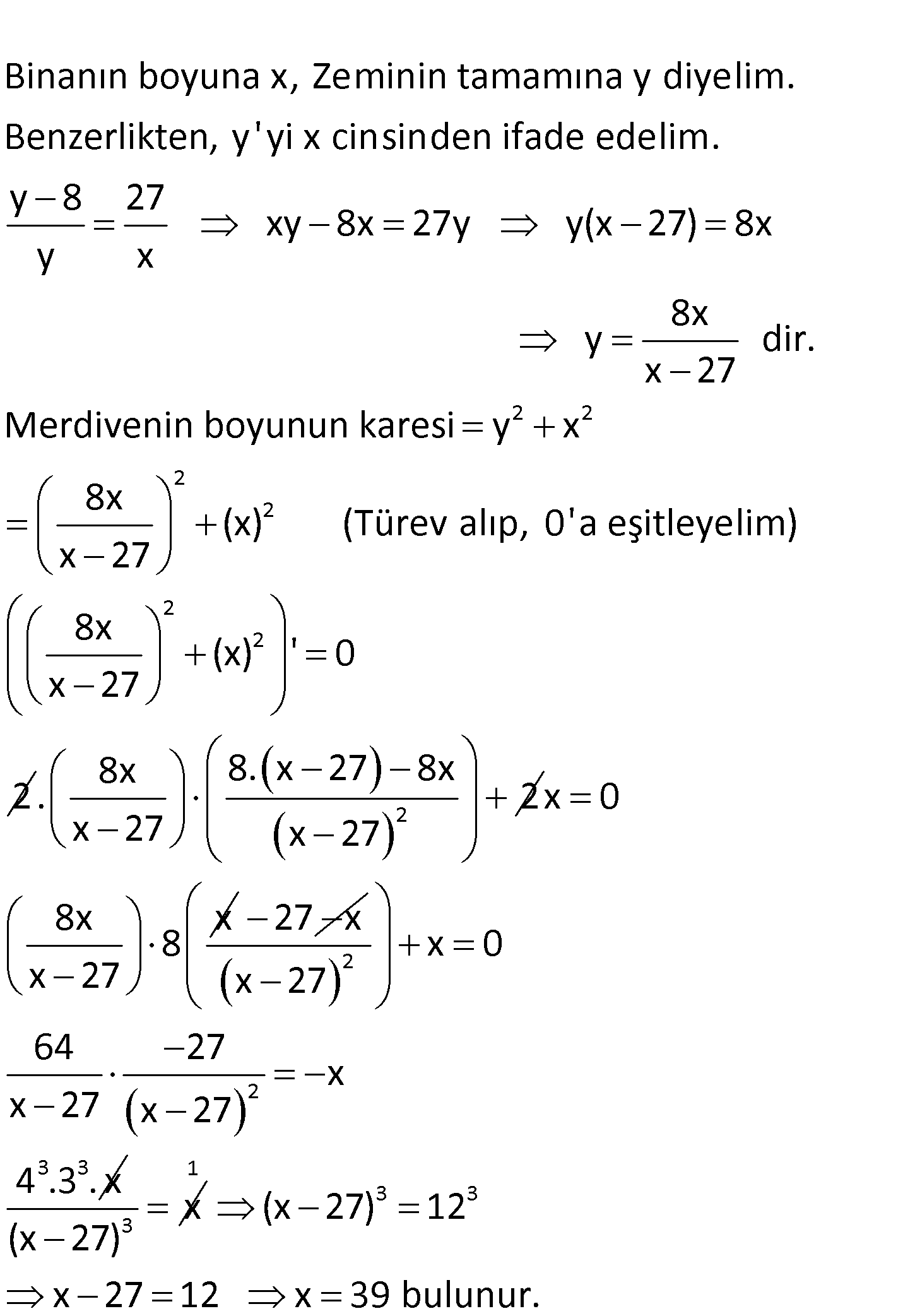
10.SORU


Burdan sonraki sorular, Fen Lisesi Müfredatı için geçerlidir.
11.SORU

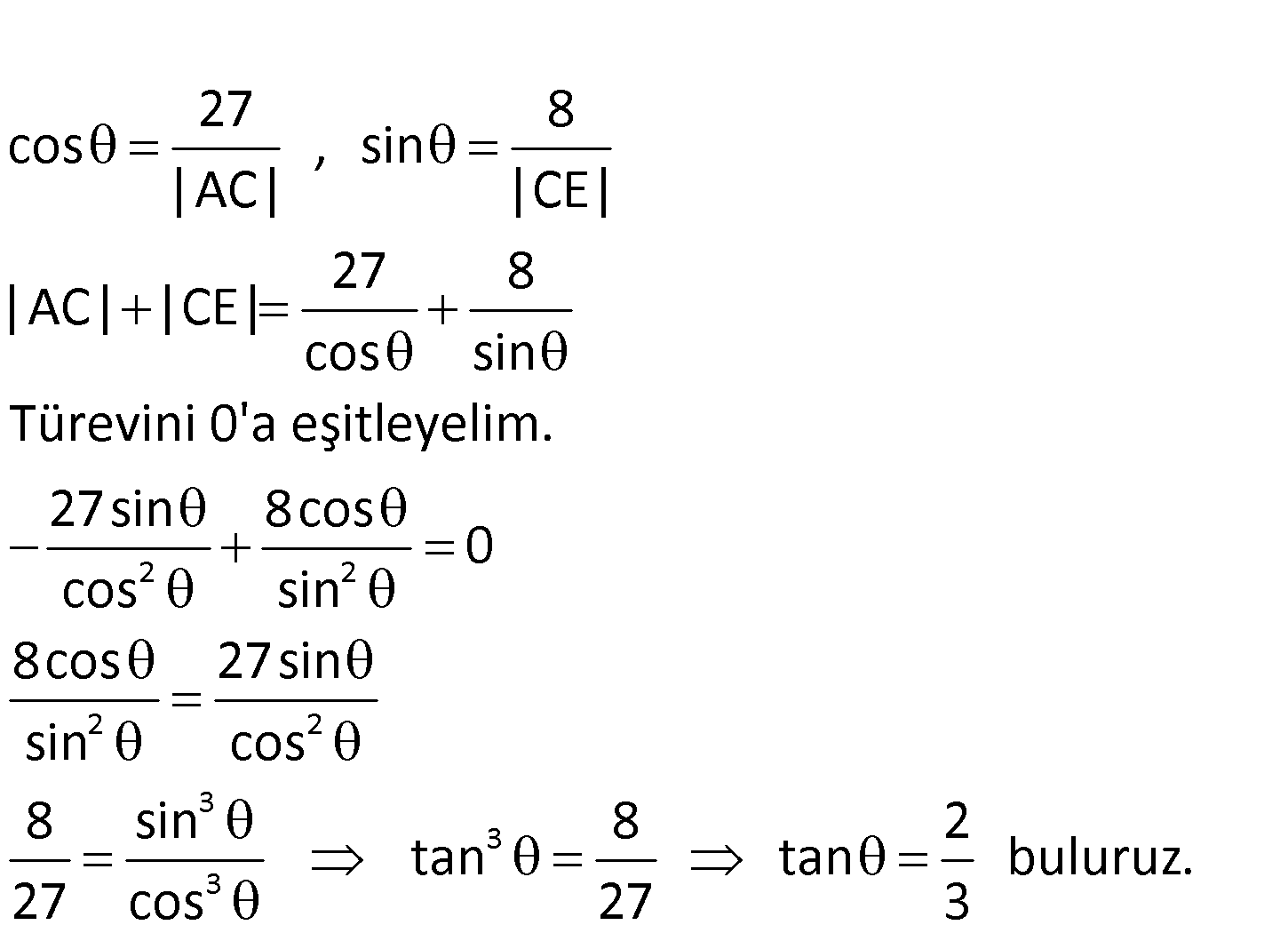
Diğer Soru Tipleri için Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
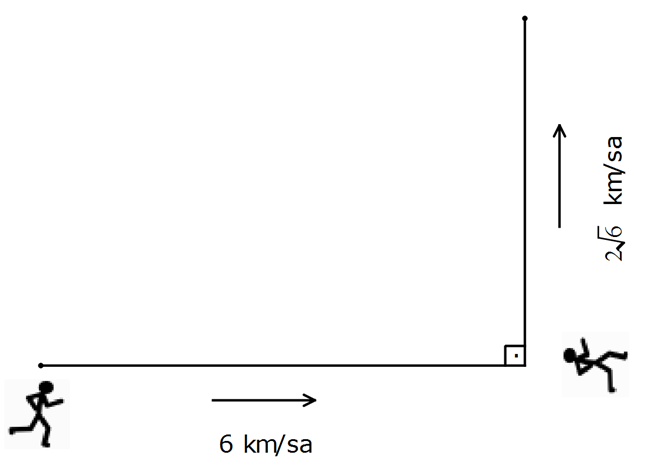
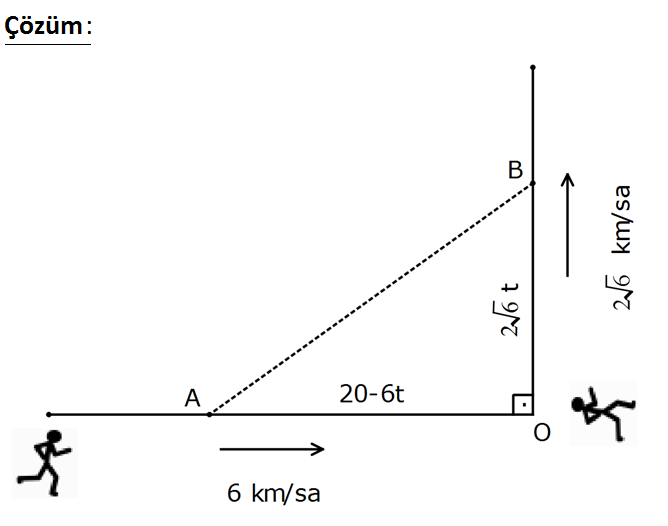
www.matematikkolay.net Aralarında 20 km bulunan iki kişi ok yönlerinde sırasıyla 6 km / sa ve 2 6 km / sa hızlarıyla hareket ediyorlar. Buna göre, kaç saat sonra aralarındaki uzaklık en az olur? A) 1 B) 2 C) 3 D) 4 E) 5 www.matematikkolay.net |AB| uzunluğu şekildeki gibi AOB üçgeninin hipote – nüsüdür. t süre sonra; |AO| 20 6t |OB| 2 6t dir. 2 2 2 2 2 2 2 2 2 |AB| |AO| |OB| |AB| (20 6t) (2 6t) 400 120t 36t 24t 400 120t 60t dir. Türev alıp, 0’a eşitleyelim. ( 400 120t 60t )’ 0 120 120t 0 120 120t 0 2 400 120t 60t t 1 dir. 40
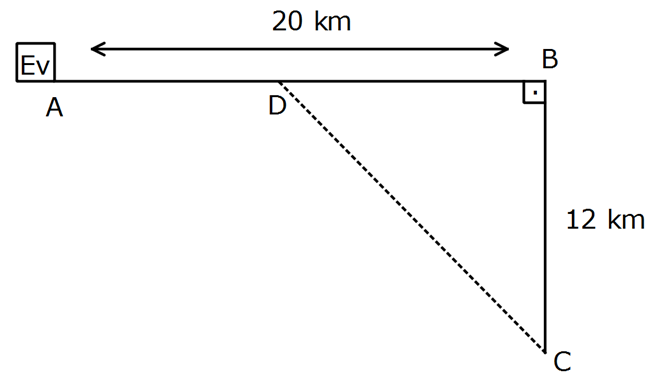
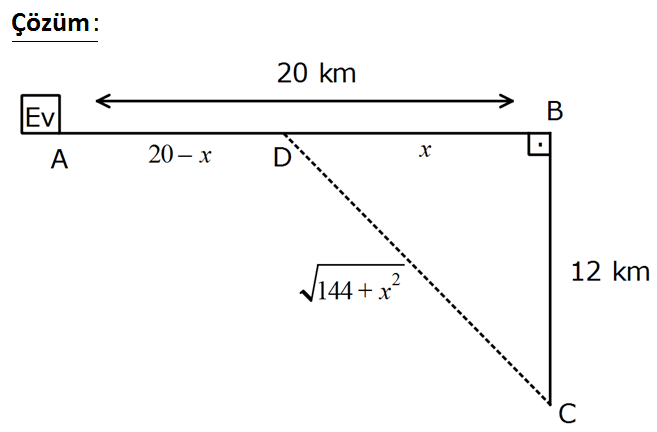
www.matematikkolay.net Sahilde B noktasına 12 km uzaklıktaki bir kişi deniz motoruyla 3 km/ dk hızla önce sahile, daha sonra B noktasına 20 km uzaklıktaki evine arabayla 5 km/ dk hızla gitmek istiyor. En kısa sürede eve ulaşmak için sahile çıktığı D nok – tasının eve uzaklığı olan AD kaç km olabilir? A) 6 B) 9 C) 11 D) 12 E) 15 : Çözüm www.matematikkolay.net 2 2 2 2 2 144 x 20 x Süre 3 5 Türev alıp, 0’a eşitleyelim. 2x 1 0 3.2. 144 x 5 x 1 5x 3 144 x 3. 144 x 5 25x 9.(1 2 2 2 2 2 44 x ) 25x 1296 9x 16x 1296 x 81 x 9 dur. |AD| 20 x 20 9 11 km buluruz. 51
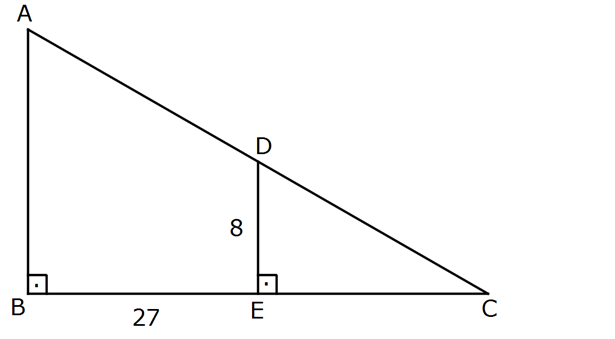
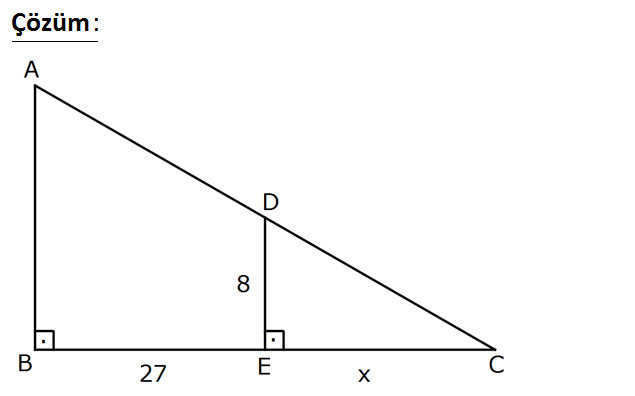
AB BC , DE // AB , BE 27 br ve ED 8 br olduğuna göre, AC nin alabileceği en küçük değer kaç birimdi r? A) 21 B) 13 13 C) 6 7 D) 5 10 E) 4 7 www.matematikkolay.net : Çözüm www.matematikkolay.net 2 2 2 |DC| x 64 pisagor x 64 |AC| (27 x) benzerlikten x x 64.(27 x) |AC| tir. Türevini 0’a x 2 2 2 2 eşitleyelim. 2x (27 x) x 64 x 1 x 64.(27 x) 2 x 64 0 x Pay kısmına bakalım. 2 x 2 2 2 2 2 2 2 2 2 2 2 3 2 3 2 (27 x) x 64 x 1 x 64.(27 x) 0 x 64 x 64 ile genişletelim. (27x x x 64)x (x 64)(27 x) 0 (27x 2x 64)x (x 64)(27 x) 0 27x 2x 64x (27x x 64.27 64x) 0 27x 3 2x 64x 2 27x 3 x 64.27 64x 3 2 x 64.27 x 4.3 12 dir. 12 64.(27 12) 208.39 4 13.39 |AC| 13 13 12 12 12 buluruz. 81
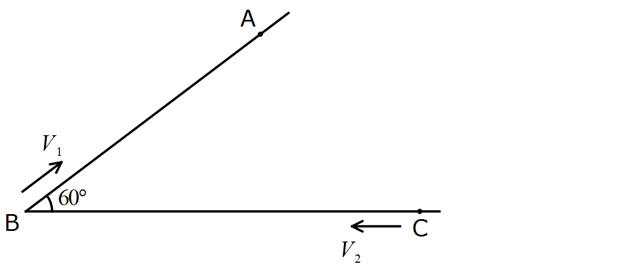
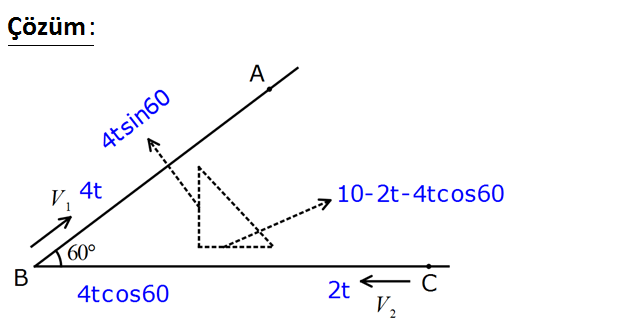
www.matematikkolay.net 1 2 1 Hızları V ve V olan araçlar şekildeki yönlerde aynı anda harekete başlıyor. V 4 km/ sa 2 V 2 km/ sa BC 10 km olduğuna göre, kaç saat sonra aralarındaki uzaklık minimum olur? 10 9 8 6 A) B) C) D) E) 1 7 7 7 7 : Çözüm 2 2 2 2 2 2 2 2 Aradaki uzaklık d ise; d (4tsin60) (10 2t 4tcos60) (2t 3) (10 4t) 12t 100 80t 16t 28t 80t 10 0 Türevini alıp, 0’a eşitleyelim. 56t 80 0 80 10 t buluruz. 56 7 www.matematikkolay.net 82
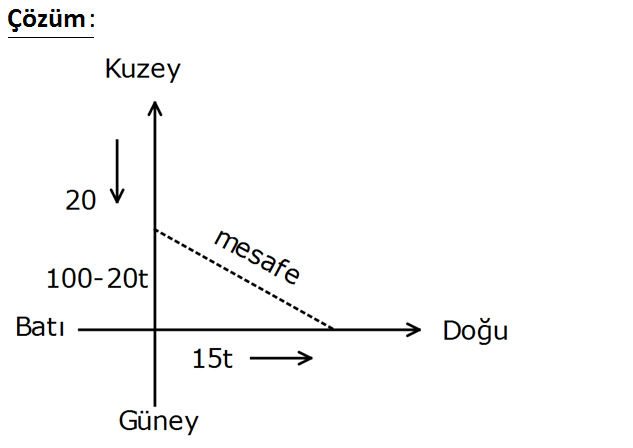
İki gemiden Birincisi koordinat düzleminde saatte 20 km hızla güneye İkincisi koordinat düzleminde saatte 15 km hızla doğuya doğru seyir halindedir. Belli bir anda ikinci gemi, birinci geminin y ekseni üzerinde 100 km güneyinde kalıyor. Bu andan itibaren kaç saat sonra gemilerin arasın – daki mesafe en az olur? 18 14 16 19 17 A) B) C) D) E) 5 5 5 5 5 www.matematikkolay.net : Çözüm Aradaki mesafe bir üçgenin hipotenüsüdür. 20 ile güneye inen araç 100 km’lik güney farkını kapatmay 2 2 a çalışacaktır. Hızı 15 olan araç, doğuya doğru her saat 15t’lik bir yol gidecektir. Bunu denkleme dökersek; Mesafe 100 20t 15t dir. Minimum değer için türev alıp, 0’a eşitleyelim. 2 100 20t 20 2 15t 15 0 40100 20t 3015t 0 4000 800t 450t 0 4000 1250t 0 1250t 4000 4000 t 16 1250 5 16 buluruz. 5 129
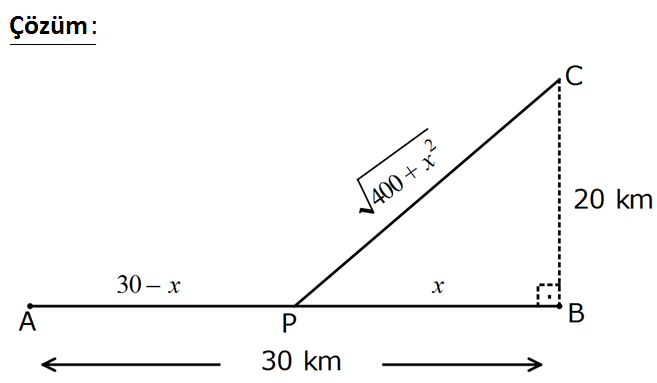
www.matematikkolay.net A kenti, doğu batı yönündeki bir karayolu üzerin – dedir. C beldesi, A nın 30 km doğusunda bulunan B beldesinin 20 km kuzeyindedir. C beldesinin bu karayoluna bağlayacak olan CP karayolu yapılacak, bu yolun bağlantı noktası ile A kenti arasındaki eski yolda da iyileştirme çalışması yapılacaktır. Yeni yapılacak yolu kilometresi 3 TL ‘ ye, iyileştirme çalışmasının kilometresi 2 TL ‘ ye mâl olmaktadır. Buna göre, yolun en düşük maliyeti kaç TL olur? A) 120 4 5 B) 100 16 5 C) 100 20 5 D) 60 16 5 E) 60 20 5 : Çözüm www.matematikkolay.net 2 2 2 İyileştirilen Yeni y yol PB x dersek, AP 30 x km olur. PC 20 x 400 x olur. Maliyet AP .2 PC apılan yol 2 2 2 2 .3 (30 x).2 400 x .3 60 2x 3 400 x liradır. Türev alıp, 0’a eşitleyerek minimum noktayı bulalım. 60 2x 3 400 x ‘ 0 2x 2 2 3 0 3 2 400 x 2 x 2 2 400 x 2 2 2 2 2 2 2 2 2 3x 1 3x 2 400 x 2 400 x 9x 4 400 x 9x 1600 4x 5x 1600 x 320 x 64.5 8 5 tir. Maliyet 60 2x 3 400 x 60 2.8 5 3 400 320 60 16 5 3 720 60 16 5 3 144.5 60 16 5 3.12 5 60 16 5 36 5 60 20 5 lira buluruz. 130
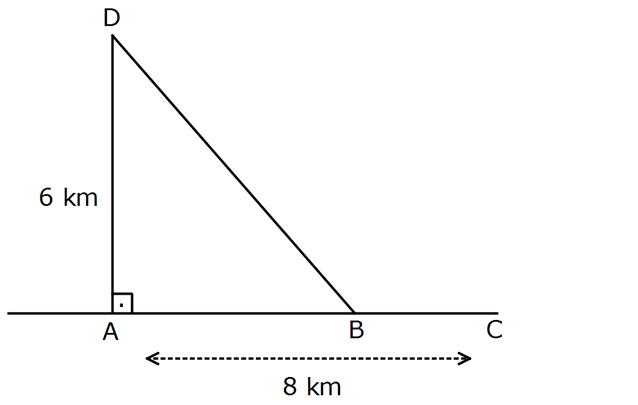
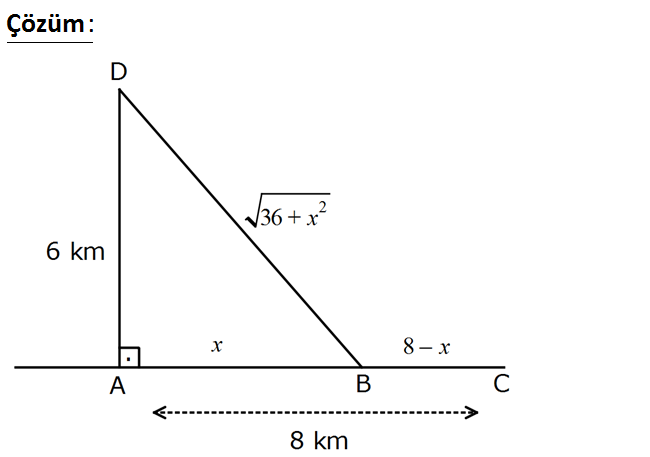
www.matematikkolay.net Yukarıdaki şekilde D noktasında kayıkta bulunan bir kişi sahildeki A noktasından 8 km uzaklıktaki C noktasına en kısa sürede ulaşmak istiyor. AC 8 km, AD AC , AD 6 km, kayığın hızı 3 km/ sa, adamın sahildeki hızı 6 km / sa olduğuna göre, kayık sahildeki A noktasından kaç km uzağa yanaştırılmalıdır? A) 7 B) 4 3 C) 6 D) 3 3 E) 2 3 : Çözüm www.matematikkolay.net 2 x 36 8 x t türev alıp, 0’a eşitleyelim. 3 6 2 x 2 2 1 0 x 36.3 6 x 3 2 1 x 36 6 2 2 2 2 2 2 2x x 36 4x x 36 3x 36 x 12 x 2 3 buluruz. 44
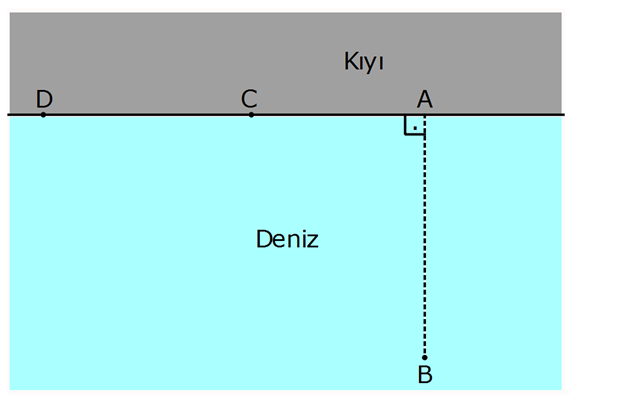
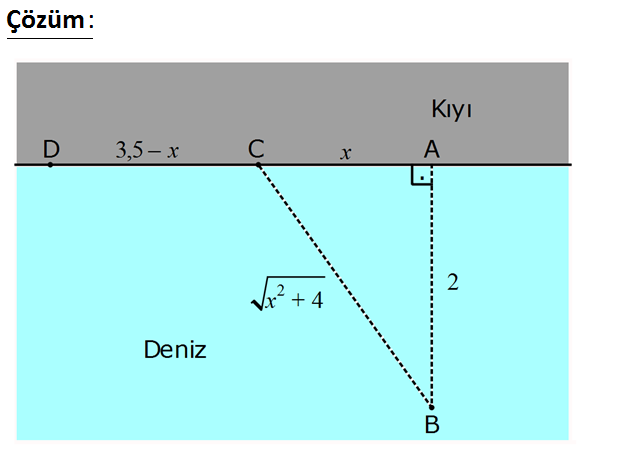
www.matematikkolay.net AB AD , AB 2 km ve AD 3,5 km dir. Şekildeki A noktasından 2 km uzakta olan B noktasındaki deniz taş ıtında bulunan Ömer Beyi A nok – tasından 3,5 km uzaktaki D noktasına deniz taşıtı ile ulaştık tan sonra C noktasından D noktasına yürüyerek gidiyor. Deniz taşıtının saatteki hızı 3 km, Ömer Bey’in kıyıdaki yürüme hızı da saatte 5 km dir. Buna göre, B noktasından D noktasına en kısa sürede ulaşan Ömer Bey ‘in C noktasından D nok – tasına kadar yürüdüğü mesafe kaç km dir? A) 3,5 B) 3 C) 2,5 D) 2 E) 1,5 : Çözüm www.matematikkolay.net 2 Taşıtla gidilen yol Yürünen yol t 3 km/sa 5 km/sa x 4 3,5 x t (türev alıp, 0’a eşitleyelim. 3 5 ) 2x 2 2 2 2 2 2 2 2 1 x 1 0 .3 x 4 5 3 x 4 5 5x 3 x 4 25x 9x 36 16x 36 36 6 x x 1,5 16 4 |CD| 3,5 x 3,5 1,5 2 buluruz. 46
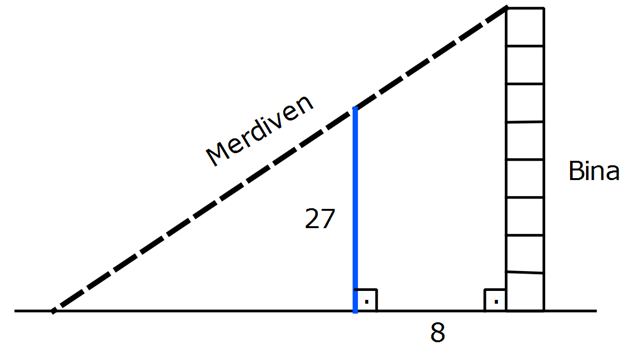
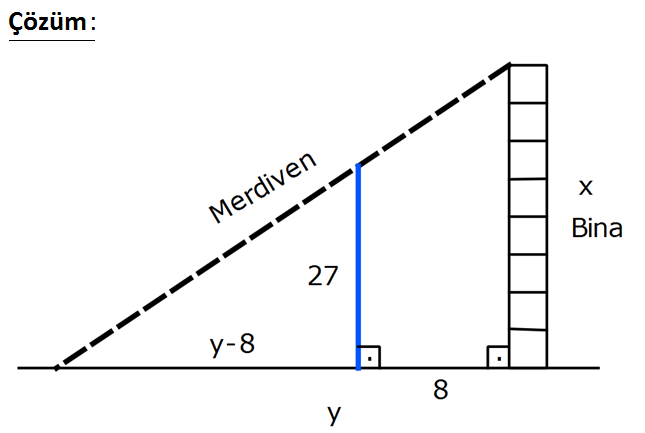
Bir binanın en üst katındaki eşyaları taşımak için binanın 8 metre gerisinde bulunan 27 metrelik desteğe dayalı en kısa merdiven koyuluyor. Buna göre, binanın yüksekliği kaç metredir? A) 30 B) 36 C) 39 D) 42 E) 45 www.matematikkolay.net : Çözüm www.matematikkolay.net Binanın boyuna x, Zeminin tamamına y diyelim. Benzerlikten, y’ yi x cinsinden ifade edelim. y 8 27 y x 2 2 2 2 xy 8x 27y y(x 27) 8x 8x y dir. x 27 Merdivenin boyunun karesi y x 8x (x) (Türev alıp, 0’a eşitleyelim) x 27 8x x 27 2 2 (x) ‘ 0 2 2 8x 8. x 27 8x . 2 x 27 x 27 x 0 8x x 8 x 27 27 x 2 2 3 3 x 0 x 27 64 27 x x 27 x 27 4 .3 . x 3 x (x 27) 1 3 3 (x 27) 12 x 27 12 x 39 bulunur. 52
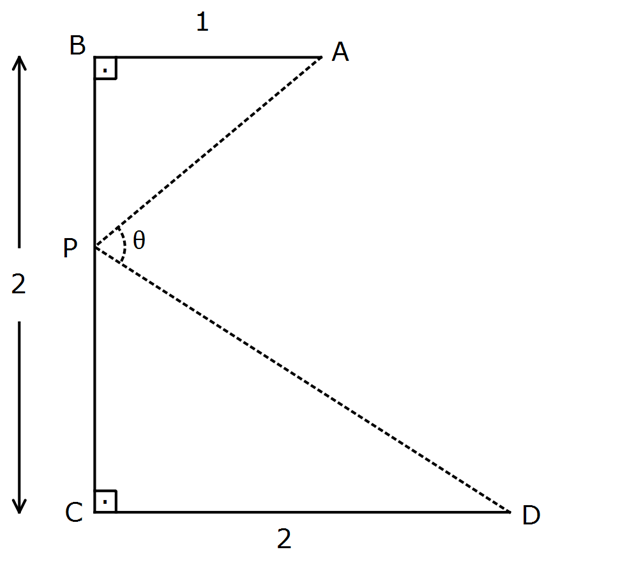
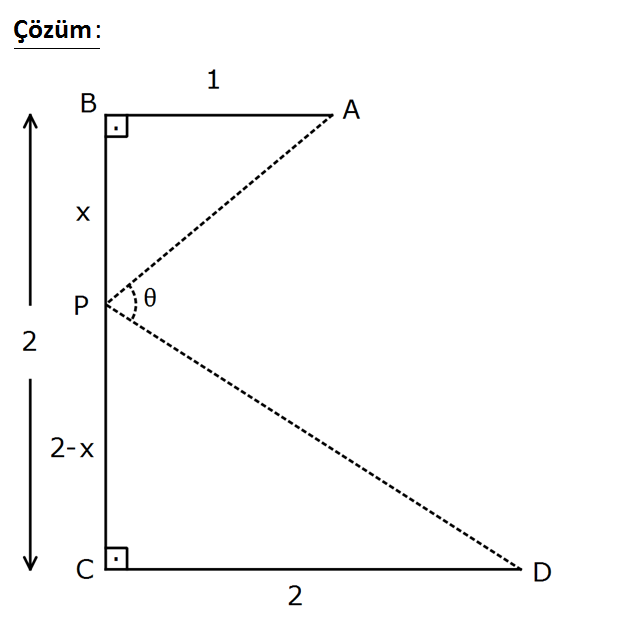
www.matematikkolay.net Yukarıdaki verilere göre, açısının en büyük değeri için P noktası B den kaç birim uzakta seçilmel idir? A) 5 2 B) 2 C) 5 1 D) 10 2 E) 10 1 : Çözüm www.matematikkolay.net www.matematikkolay.net x tana 1 1 2 x tanb dir. 2 a b olduğundan, tana tanb tan tan a b 1 tana. tanb 2 x 2x 2 x x 2 2 2 x 1 x 1 2 2 x 2 2 2x x 2 2 2 2x x 2 2 2 2 2 2 2 x 2 x 2x 2 x 2 tan x 2x 2 en büyük olduğunda tan değeri de en büyük olur. tan nin en büyük değeri için türev alıp, 0’a eşitleyelim. x 2 1. x 2x 2 2x 2 x 2 ‘ x 2x 2 x 2x 2 0’a eşitleyeceğimiz 2 2 2 2 2 2 2 2 2 2 için paydaya bakmaya gerek yok. 1. x 2x 2 2x 2 x 2 0 x 2x 2 2x 2x 4x 4 0 x 2x 2 2x 2x 4x 4 0 x 4x 6 0 x 4x 6 0 x 4x 4 10 0 x 2 10 0 x 2 10 x 2 10 x 10 2 buluruz. 68
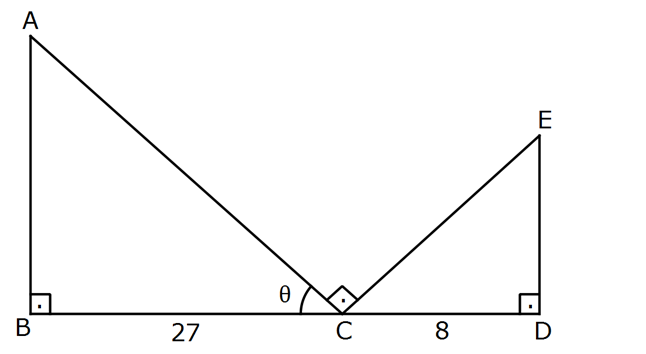
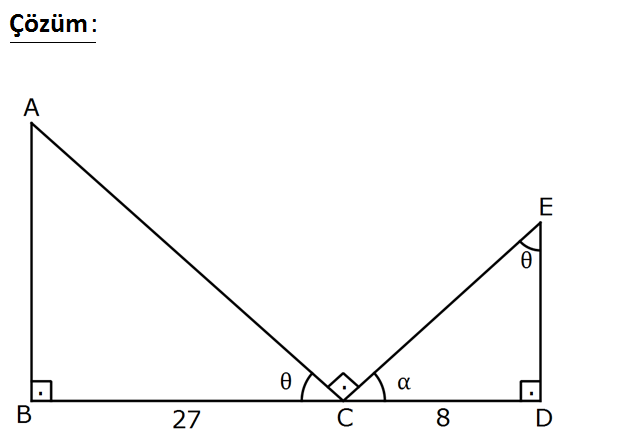
AB BD , AC CE , ED CD CD 8 cm, BC 27 cm olduğuna göre, tan nın hangi değeri için AC EC toplamı en küçü k olur? 1 1 1 2 3 A) B) C) D) E) 4 3 2 3 4 www.matematikkolay.net : Çözüm 2 2 27 8 cos , sin |AC| |CE| 27 8 |AC| |CE| cos sin Türevini 0’a eşitleyelim. 27sin 8cos 0 cos sin 2 2 3 3 3 8cos 27sin sin cos 8 sin 8 2 tan tan buluruz. 27 cos 27 3 43

