Soru Sor sayfası kullanılarak Türevin Anlamı konusu altında Prizma Maksimum Minimum ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU

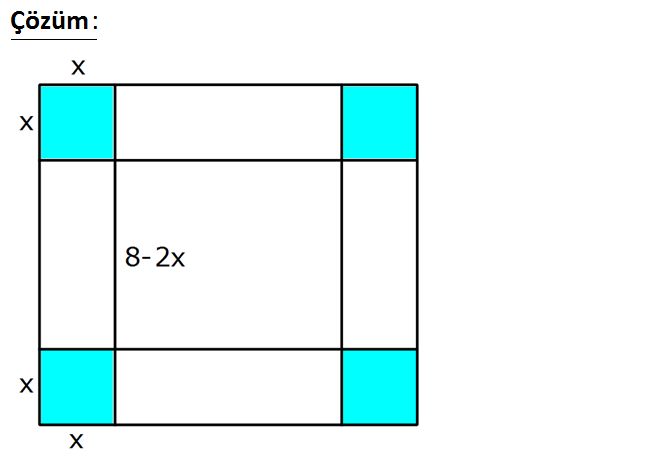

2.SORU

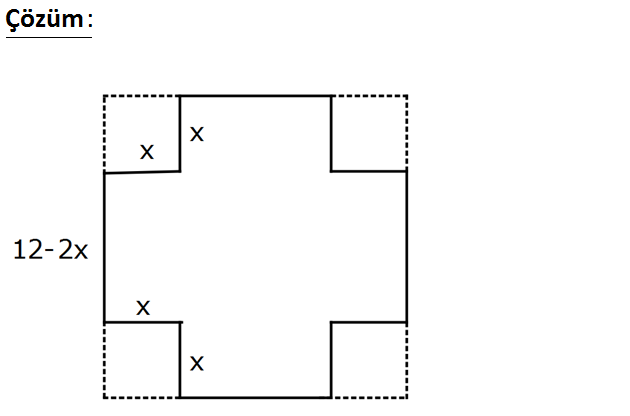

3.SORU


Diğer Soru Tipleri için Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
Kenar uzunluğu 8 cm olan kare biçimindeki bir kar – tonun dört köşesinden eş kareler çıkarılıyor. Ge 3 riye kalan karton katlanarak üstü açık bir kutu elde ediliyor. Elde edilen en büyük hacimli kutunun hacmi kaç cm olur? 1024 953 721 A) B) C) D) 13 E) 12 27 27 27 www.matematikkolay.net : Çözüm Çıkarılan karelerin bir kenarı x cm olsun. Kutunun taban alanını oluşturan karenin bir kenarı 8 2x c 2 2 2 2 2 m olur. Kutunun yüksekliği de x cm olur. O zaman bu kutunun hacmi; Hacim 8 2x x ile hesaplanır. Türev alıp, 0’a eşitleyelim. Maksimum nokta için 8 2x x ‘ 0 2 8 2x 2 x 8 2x 0 4x 8 2x 8 2x 0 8 2x 4x 8 2x 2 2 2 2 8 2x 4x 8 4 8 6x x ‘ te maksimumdur. 6 3 4 4 8 4 Hacim 8 2x x 8 2 8 3 3 3 3 16 4 256 4 1024 buluruz. 3 3 9 3 27 www.matematikkolay.net 128
Bir kenarı 12 cm olan kare şeklindeki bir karton, köşelerinden eşit kareler kesilip katlanarak üst 3 ü açık bir kutu yapılacaktır. Buna göre, kutunun hacmi en çok kaç cm tür? A) 64 B) 128 C) 160 D) 256 E) 512 www.matematikkolay.net : Çözüm 2 2 Kare dik prizmanın taban alanı 12 2x Yüksekliği de x birim olacaktır. Buna göre; Hacmi 12 2x x tir 2 2 2 2 . Maksimum değeri bulmak için türev alıp, 0’a eşitleyelim. 12 2x x ‘ 0 2 12 2x 2 x 12 2x .1 0 4 12 2x x 12 2x .1 0 12 2x 4 12 x 2 2 3 x 12 2x 4x 12 6x x 2 dir. Hacim 12 2.2 .2 8 .2 128 cm buluruz. 148
3 2 4 br hacimli st aç k bir kare dik prizma yapmak i in kullan lan bir levha en az ü ü ı ç ı kaç br olabilir? 2 2 : Kare dik prizmanın taban ayrıtlarına x diyelim. 4 Hacim x .h 4 h dir. x Bu kare dik prizm Çözüm 2 2 2 2 2 2 3 3 2 anın yüzey alanı; 4 16 Taban Yanal Alan x 4x x tir. x x Türev alıp, 0’a eşitleyelim. 16 16 16 x ‘ 0 2x 0 2x x x x 2x 16 x 8 x 2 dir. 16 16 x 2 için x 4 x 4 8 12 buluruz. 2 www.matematikkolay.net 54

