Soru Sor sayfası kullanılarak Türevin Anlamı konusu altında Grafikte Teğetin Eğimi ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU


2.SORU


3.SORU


4.SORU
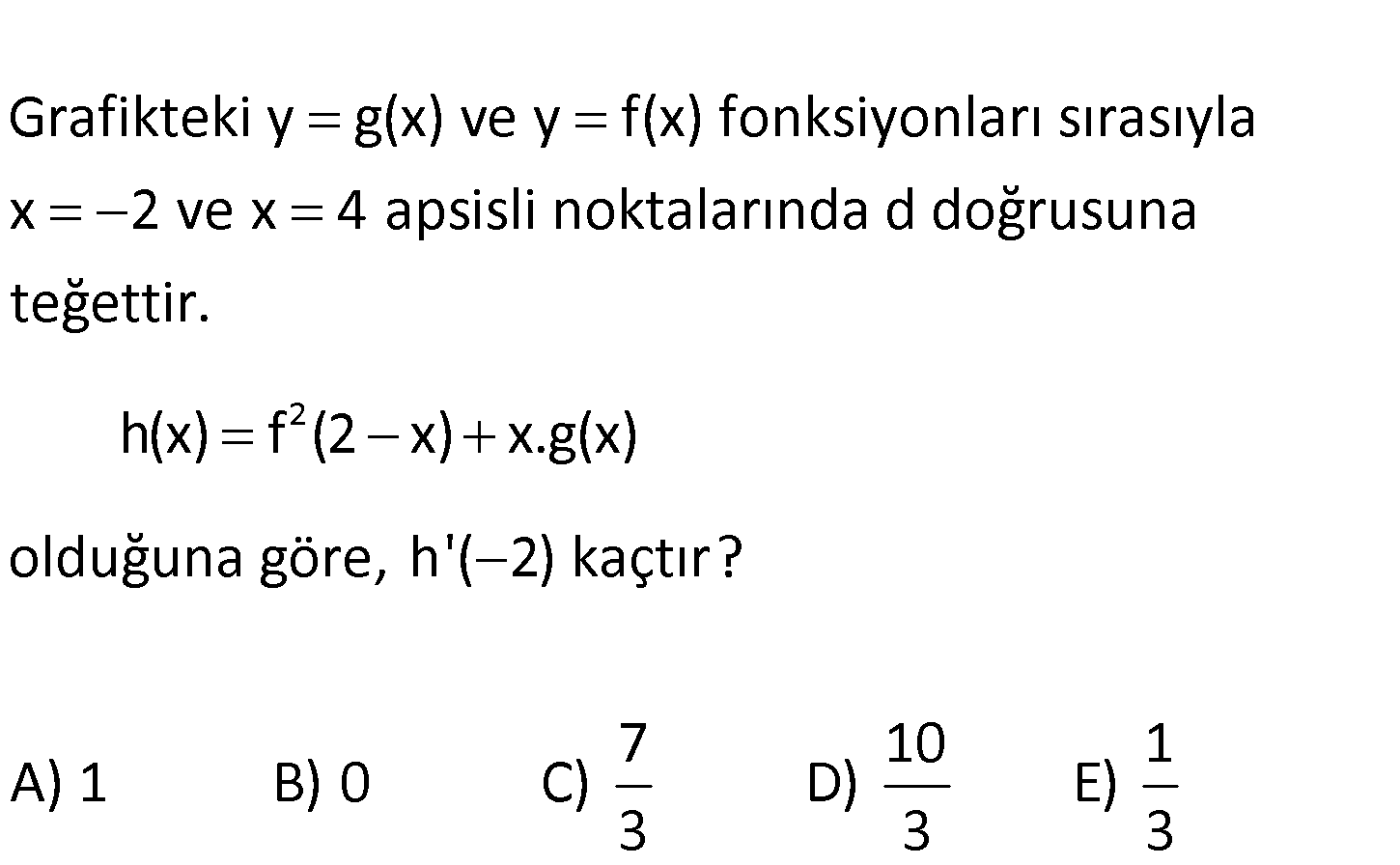
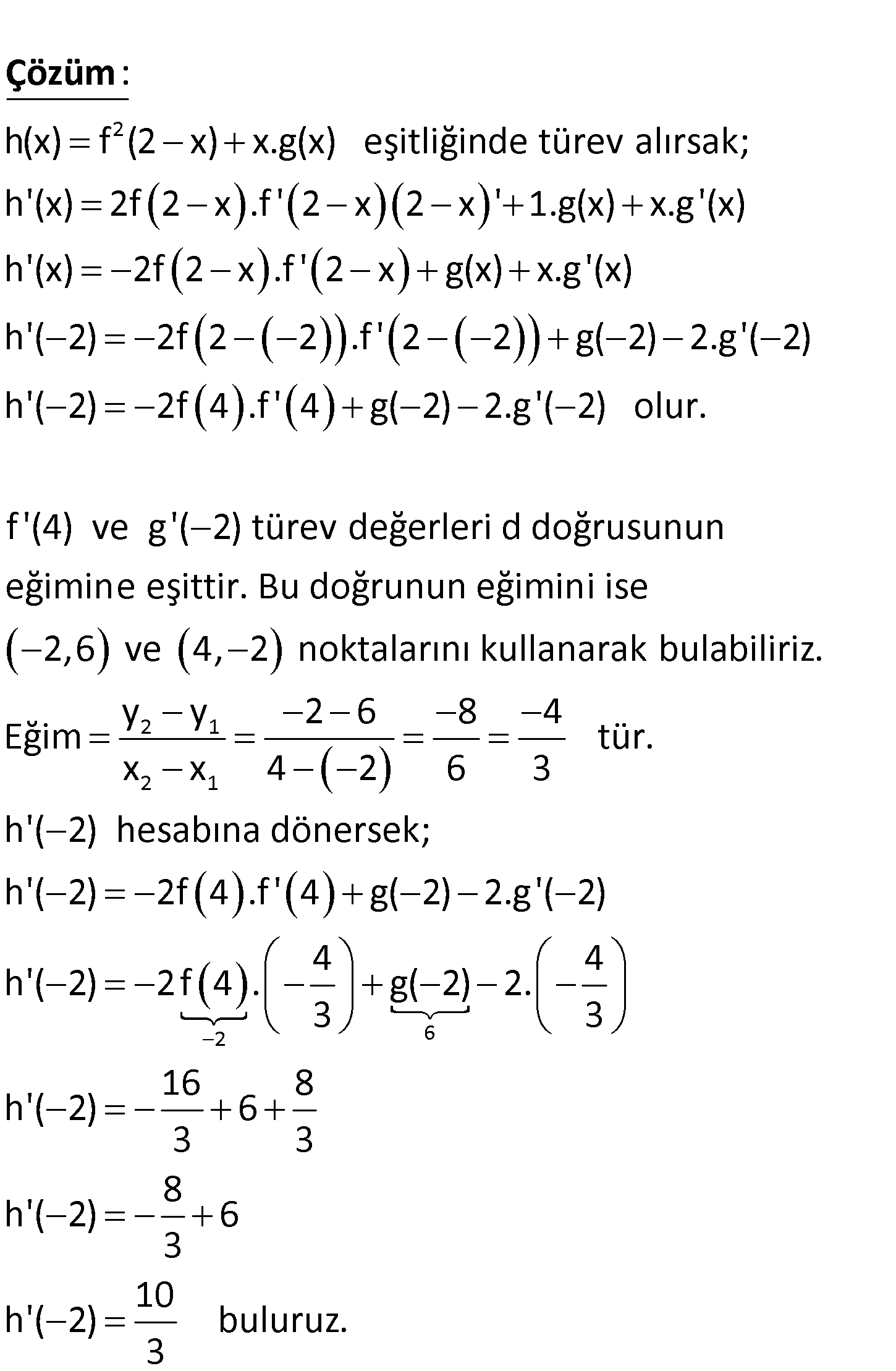
5.SORU
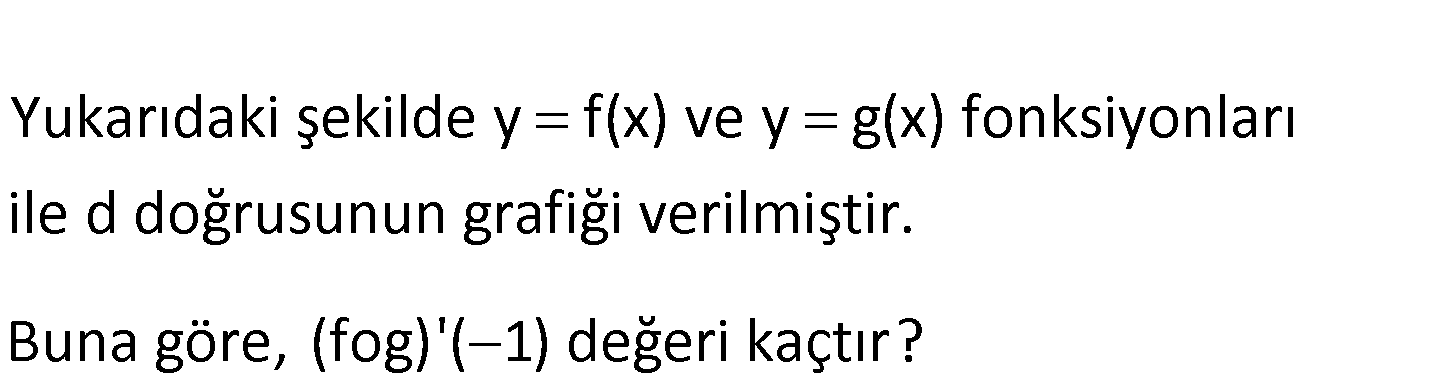

6.SORU
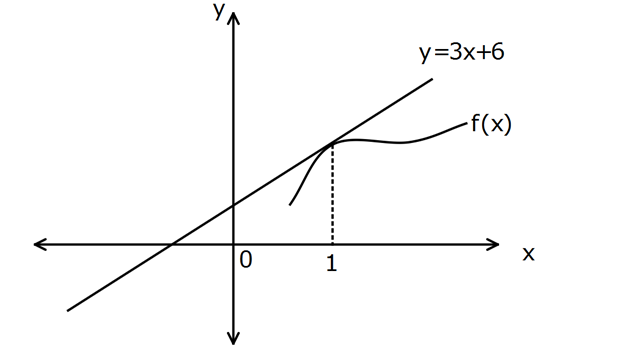
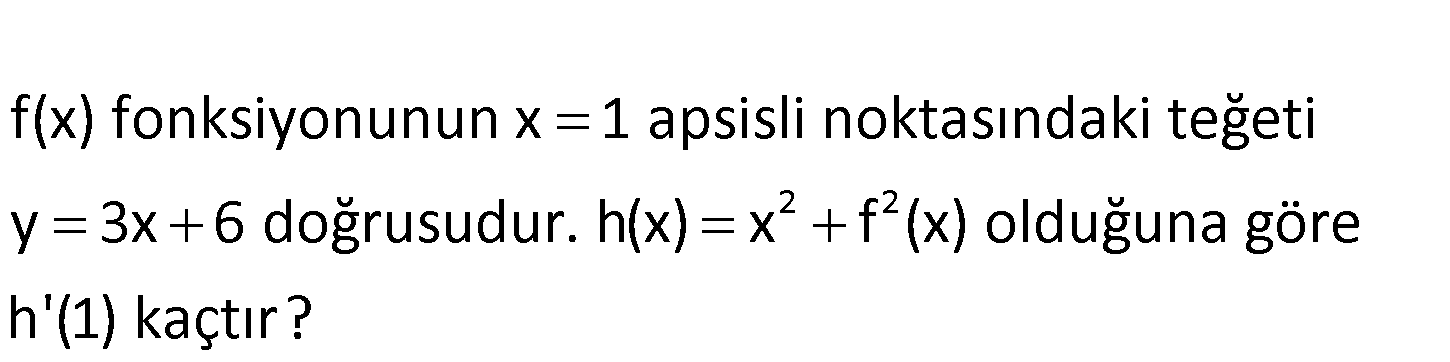

7.SORU
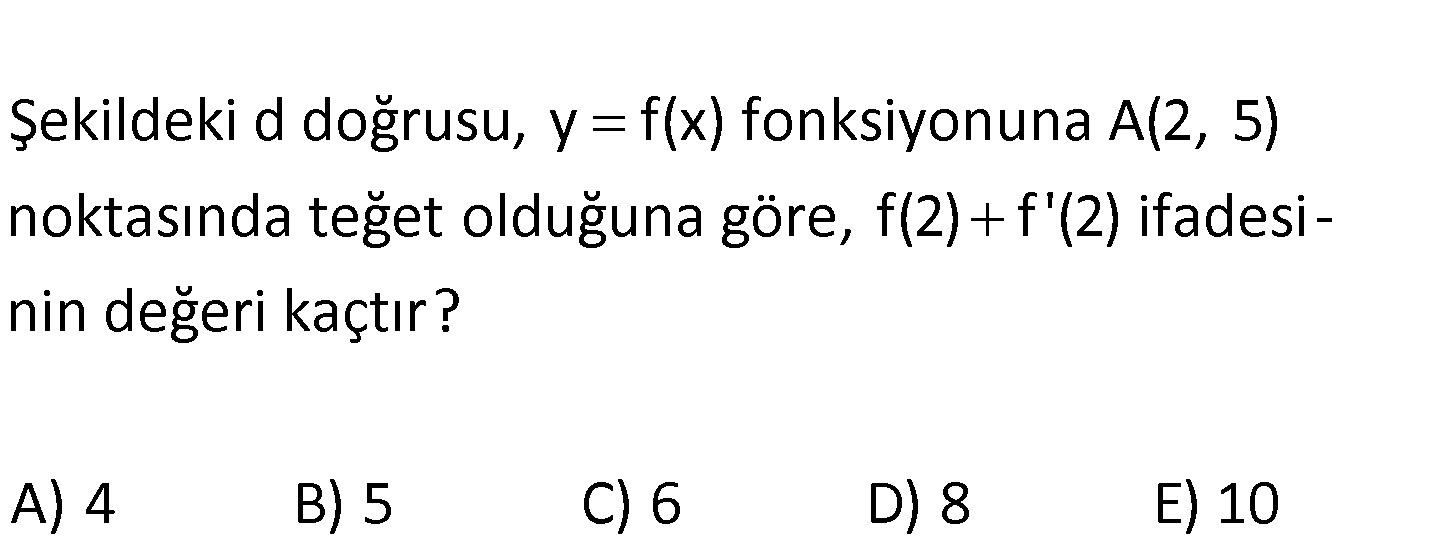

8.SORU
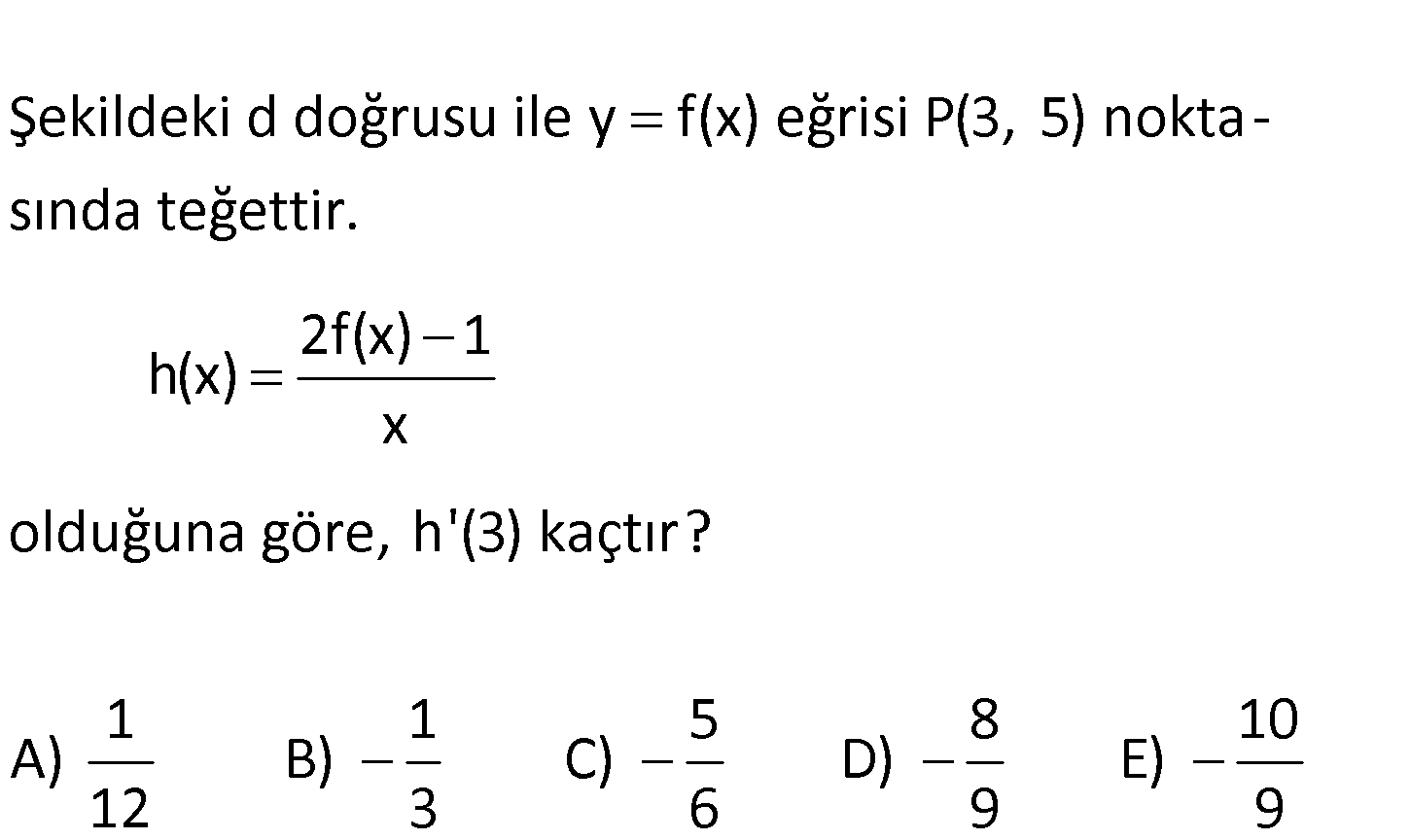

9.SORU


Diğer Soru Tipleri için Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
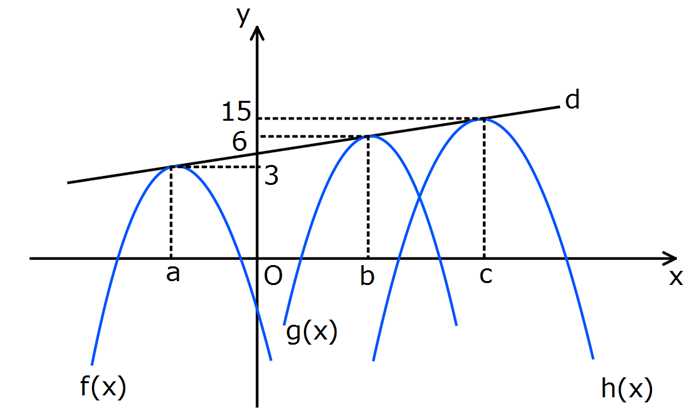
www.matematikkolay.net Şekilde f, g ve h fonksiyonlarının d doğrusuna hangi noktada teğet oldukları gösterilmiştir. Buna gö f ‘(a) h'(c) re, kaçtır? g'(b) Verilen noktalardaki teğet doğrusu, hep aynı doğru olduğundan eğimler eşittir. Dolayısıy : la da Çözüm türevleri eşittir. f ‘(a) h'(c) m m 2m 2 buluruz. g'(b) m m 49
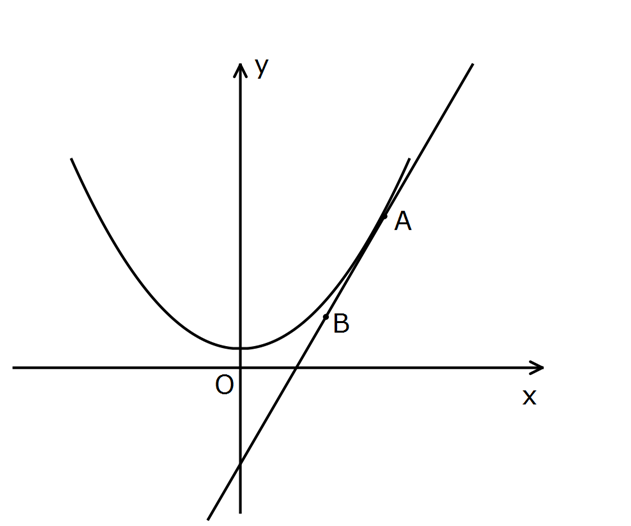
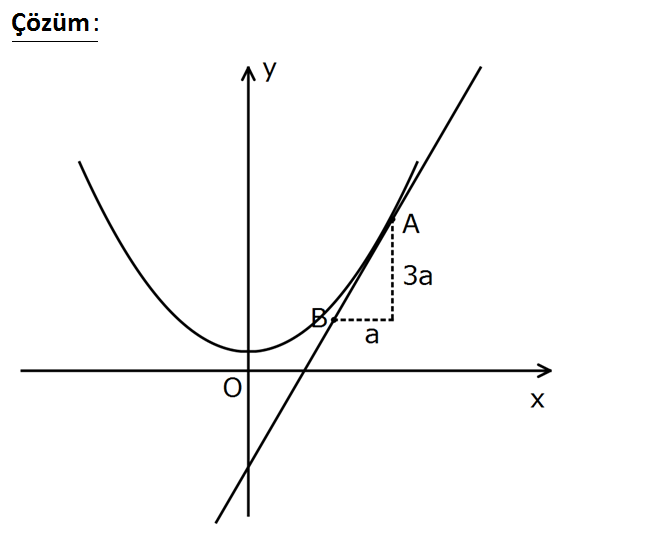
2 Yukarıdaki şekilde y x 1 parabolünün üzerindeki 3 13 A , noktasından çizilen teğetin üzerind 2 4 e değme noktasından itibaren AB 1 br olacak şekil – de bir B noktası alınmıştır. Buna göre, A noktasının apsisi B noktasının apsisinden kaç fazladır? 1 2 5 3 10 A) B) C) D) E) 5 5 5 10 10 : Çözüm www.matematikkolay.net 2 y x 1 y’ 2x 3 y’ 2 3 eğim 3 tür. 2 AB kenarı bir dik üçgenin hipotenüsü olsa; x eksenine paralel 2 2 2 2 2 kenar a birim, y eksenine paralel olan kenar 3a birim olurdu. a (3a) 1 a 9a 1 1 10 10a 1 a dur. 10 10 x eksenine paralel uzunluk a birim kabul etmiştir. 10 Bu zaten apsisler arasındaki farktır. 10 55
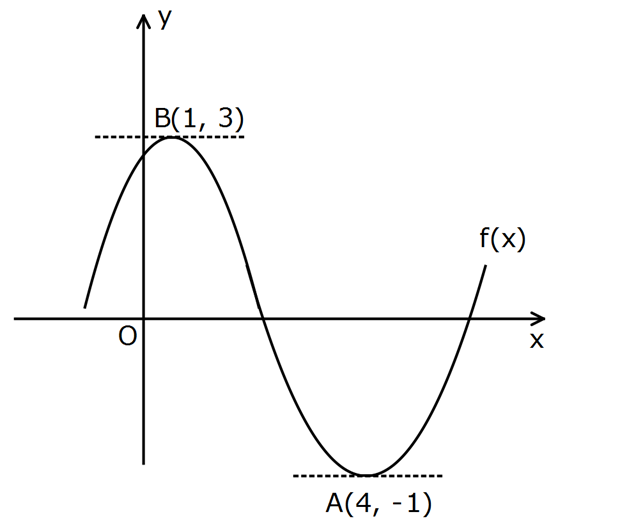
www.matematikkolay.net Şekilde y f(x) fonksiyonunun grafiği ile A(4, 1) ve B(1, 3) noktalarındaki teğetleri verilmişt . g ir 2 (x) x .f(x) olduğuna göre, g'(1) kaçtır? 2 2 g(x) x .f(x) türev alalım. g'(x) 2x.f(x) x .f ‘(x) x 1 yazalım. g'(1) 2.1.f(1) 1.f ‘(x) g'(1 : Çözüm grafikte eğim 0 ) 2f(1) f ‘(1) g'(1) 2.3 0 g'(1) 6 buluruz. 60
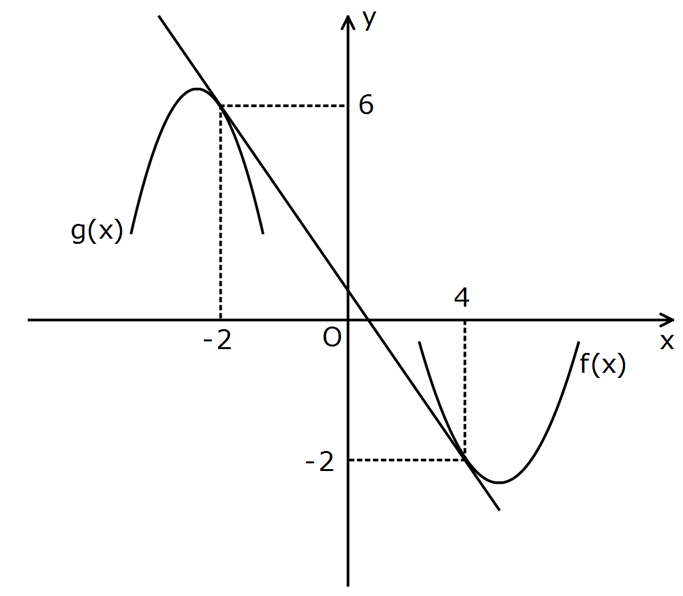
www.matematikkolay.net Grafikteki y g(x) ve y f(x) fonksiyonları sırasıyla x 2 ve x 4 apsisli noktalarında d doğrusuna teğ 2 ettir. h(x) f (2 x) x.g(x) olduğuna göre, h'( 2) kaçtır? 7 10 1 A) 1 B) 0 C) D) E) 3 3 3 www.matematikkolay.net 2 h(x) f (2 x) x.g(x) eşitliğinde türev alırsak; h'(x) 2f 2 x .f ‘ 2 x 2 x ‘ 1.g(x) x.g'(x) h : ‘(x) 2 Çözüm f 2 x .f ‘ 2 x g(x) x.g'(x) h'( 2) 2f 2 2 .f ‘ 2 2 g( 2) 2.g'( 2) h'( 2) 2f 4 .f ‘ 4 g( 2) 2.g'( 2) olur. f ‘(4) ve g'( 2) türev değerleri d doğrusunun eğimine eşittir. Bu doğrunun eğimini ise 2,6 ve 4, 2 n 2 1 2 1 2 6 oktalarını kullanarak bulabiliriz. y y 2 6 8 4 Eğim tür. x x 4 2 6 3 h'( 2) hesabına dönersek; h'( 2) 2f 4 .f ‘ 4 g( 2) 2.g'( 2) 4 4 h'( 2) 2f 4 . g( 2) 2. 3 3 16 8 h'( 2) 6 3 3 8 h'( 2) 6 3 h 10 ‘( 2) buluruz. 3 67
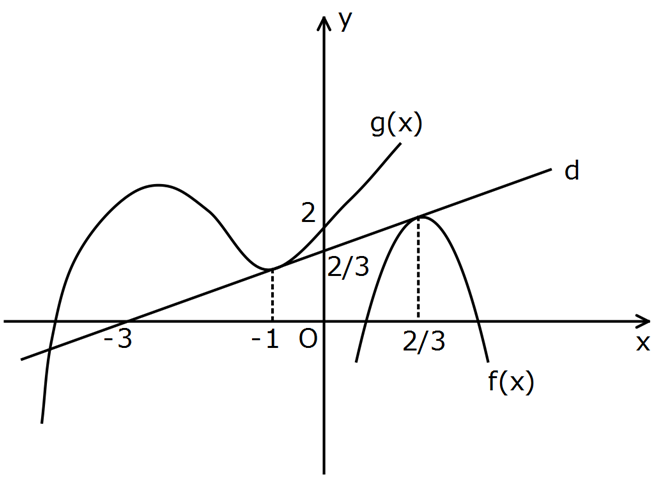
www.matematikkolay.net Yukarıdaki şekilde y f(x) ve y g(x) fonksiyonları ile d doğrusunun grafiği verilmiştir. Buna göre, (fog)'(1) değeri kaçtır? 2 1 2 1 2 2 0 y y 3 3 1 d doğrusunun eğimi x x 1 ( 3) 2 3 (fog)'( 1) g'( 1).f ‘(g( 1)) : Çözüm 2 g'( 1).f ‘ 3 2 g'( 1).f ‘ 3 d doğrusunun d doğrusunun eğimi eğimi 1 1 1 buluruz. 3 3 9 www.matematikkolay.net 69
www.matematikkolay.net 2 2 f(x) fonksiyonunun x 1 apsisli noktasındaki teğeti y 3x 6 doğrusudur. h(x) x f (x) olduğuna göre h’ (1) kaçtır? 1 eğim f(1) 3x 6 3 6 9 dur. y 3 x 6 doğrusunun eğimi 3 tür. f(x)’in x 1’deki türevi, teğe n : ti Çözüm 2 2 eğimini verir. O halde; f ‘(1) 3 tür. h(x) x f x Türev alalım. h'(x) 2x 2f(x)f ‘(x) olur. x 1 yazalım. h'(1) 2.1 2f(1)f ‘(1) h'(1) 2 2.9.3 h'(1) 2 54 h'(1) 56 buluruz. 144
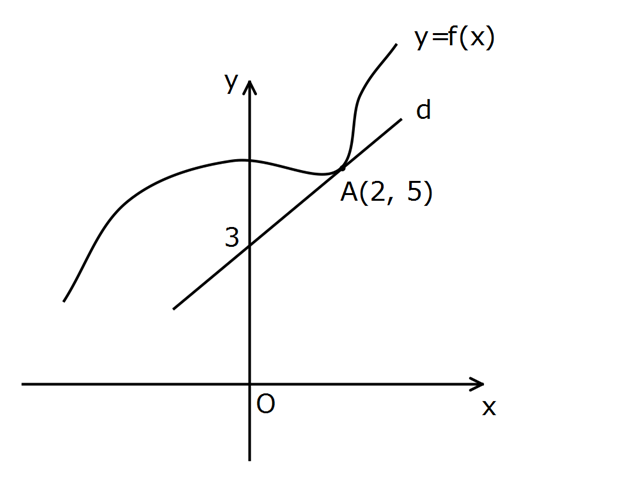
www.matematikkolay.net Şekildeki d doğrusu, y f(x) fonksiyonuna A(2, 5) noktasında teğet olduğuna göre, f(2) f ‘(2) ifades i – nin değeri kaçtır? A) 4 B) 5 C) 6 D) 8 E) 10 2 1 2 1 f ‘(2) 2 noktasındaki teğetin eğimidir. y y 5 3 2 Teğetin eğimi ise 1 dir. x x 2 0 2 : Bun Çözüm a göre; f(2) f ‘(2) 51 6 buluruz. www.matematikkolay.net 28
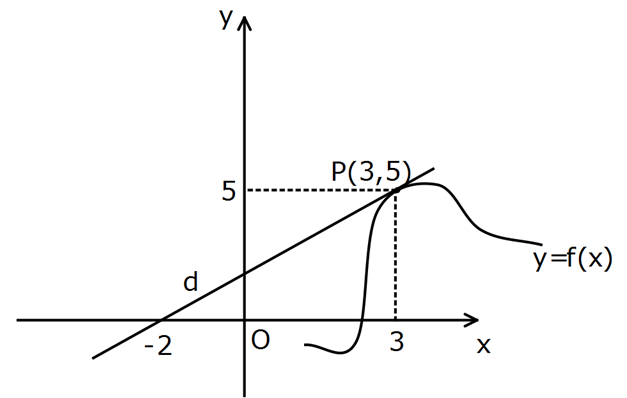
Şekildeki d doğrusu ile y f(x) eğrisi P(3, 5) noktasında teğettir. 2f(x) 1 h(x) x olduğun a göre, h'(3) kaçtır? 1 1 5 8 10 A) B) C) D) E) 12 3 6 9 9 2 5 0 5 f ‘(3) 3 noktasındaki eğim 1 dir. 3 ( 2) 5 2f ‘(x).x 1.(2f(x) 1) h'(x) dir. (Bölmen x : Çözüm 2 in türevi) Buna göre; 2f ‘(3).3 1.(2f(3) 1) 2.1.3 1.(2.5 1) h'(3) 3 9 6 9 3 1 buluruz. 9 9 3 www.matematikkolay.net 29
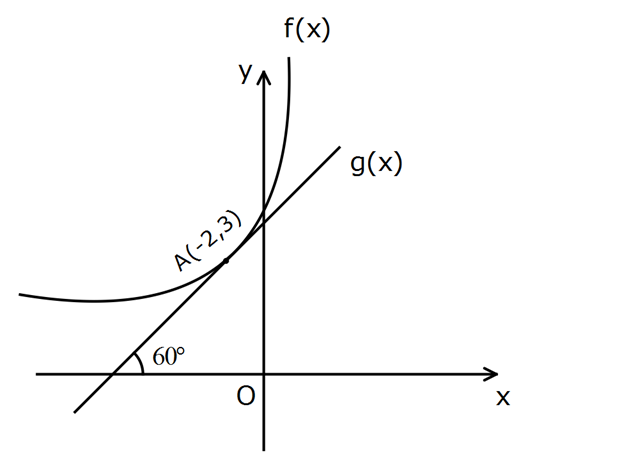
f(x) ile g(x) A noktasında teğettir. f(x) h(x) olduğuna göre, h'( 2) ifadesinin eşiti g(x) aşa a ğıd k ilerden hangisidir? A) 3 B) 0 C) 3 D) 1 E) 3 www.matematikkolay.net x 2 noktasında; f(x)’in teğetinin eğimi tan60 3 olduğu için; f ‘( 2) 3 tür. g(x)’in ise her z : Çözüm 2 2 2 aman eğimi 3 tür. g'(x) 3 tür. f(x) f ‘(x)g(x) g'(x)h(x) h(x) h'(x) dir. g(x) g (x) f ‘( 2)g( 2) g'( 2)f( 2) 3.3 3.3 h'( 2) g ( 2) 3 0 buluruz. 22

