Soru Sor sayfası kullanılarak Türevin Anlamı konusu altında x eksenini kaç noktada keser, kaç kökü vardır, 3 noktada kesiyorsa ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU


2.SORU


3.SORU


4.SORU
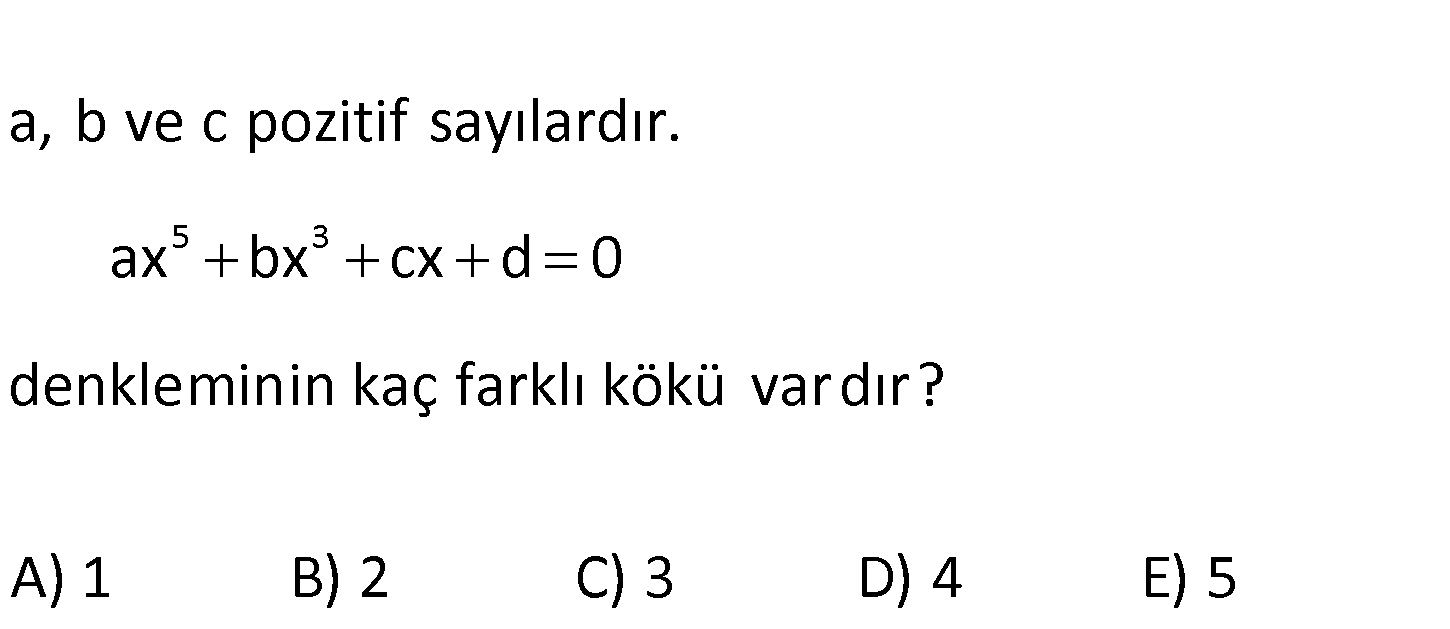

5.SORU


6.SORU


Diğer Soru Tipleri için Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
3 f(x) x 6x 4 fonksiyonu x eksenini kaç farklı noktada keser? A) 0 B) 1 C) 2 D) 3 E) 4 www.matematikkolay.net 3 2 f(x) x 6x 4 türev alınca; f ‘(x) 3x 6 olur. Bu değer sürekli pozitiftir. Demek ki f : Çözüm 3 (x) fonksiyonu sürekli ar tan bir fonksiyondur. Bu da f(x)’in , x eksenini en fazla 1 kere kese – bileceğini gösteriyor. f(x) x 6x 4 fonksiyonu negatif değerler alabili – yor. Örneğin, x 0 için f(x) 4 tür. Bu fonksiyon, daha sonraki değerler için artışa geçeceği için, x eksenini 1 kere kesecektir. 42
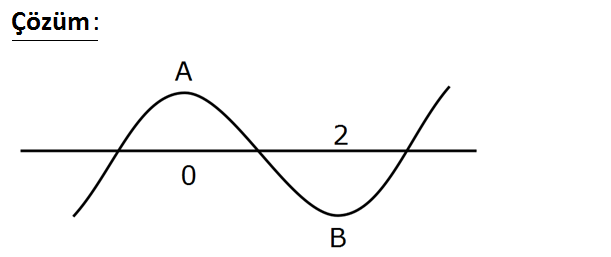
www.matematikkolay.net 3 2 f(x) x 3x 3m 18 fonksiyonu yatay ekseni üç farklı noktada kestiğine göre, m tam sayı olarak h angi değeri alınmalıdır? A) 8 B) 7 C) 6 D) 5 E) 3 : Çözüm www.matematikkolay.net Bu eğri x eksenini 3 farklı noktada kesiyorsa, yukarı – daki gibi bir grafiğe sahiptir. İki tane ext 3 2 2 3 2 remum noktası var dır. (A ve B noktası) Bunları bulmak için türev alalım. (Bu noktalarda türev 0’a eşittir.) y x 3x 3m 18 y’ 3x 6x 0 3x(x 2) x 0 veya x 2 dir. A noktasının ordinatını bulalım. y (0) 3 0 3 2 3m 18 3m 18 dir. A noktasının ordinatı 0’dan büyük olduğuna göre; 3m 18 0 m 6 dır. B noktasının ordinatını bulalım. y (2) 3 2 3m 18 8 12 3m 18 4 3m 18 3m 22 B noktasının ordinatı 0’dan küçü k olduğuna göre; 22 3m 22 0 m tür. O halde m değeri 3 22 6, aralığında olmalıdır. 3 Tam sayı olarak sadece 7 değerini alabilir. Cevap: B 112
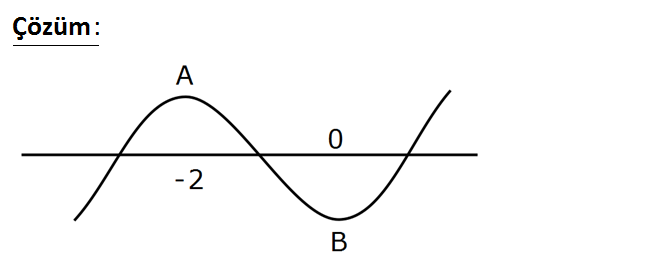
www.matematikkolay.net 3 2 y x 3x k eğrisi x eksenini 3 farklı noktada kestiğine göre, k’nin değer aldığı en geniş aral ık aşağıdakilerden hangisidir? A) (4, 8) B) (0, 4) C) (-4,-1) D) (-4, 0) E) (-4,4) : Çözüm www.matematikkolay.net Bu eğri x eksenini 3 farklı noktada kesiyorsa, yukarı – daki gibi bir grafiğe sahiptir. İki tane ext 3 2 2 3 2 remum noktası var dır. (A ve B noktası) Bunları bulmak için türev alalım. (Bu noktalarda türev 0’a eşittir.) y x 3x k y’ 3x 6x 0 3x(x 2) x 2 veya x 0 dır. A noktasının ordinatını bulalım. y ( 2) 3 2 3 2 k 8 12 k k 4 tür. A noktasının ordinatı 0’dan büyük olduğuna göre; k 4 0 k 4 tür. B noktasının ordinatını bulalım. y (0) 3 0 k k dır. B noktasının ordinatı 0’dan küçük olduğuna göre; k 0 dır . O halde k değeri 4,0 aralığında olmalıdır. 113
5 3 a, b ve c pozitif sayılardır. ax bx cx d 0 denkleminin kaç farklı kökü var dır? A) 1 B) 2 C) 3 D) 4 E) 5 www.matematikkolay.net 5 3 4 2 Pozitif Pozitif Poz. Poz Poz f(x) ax bx cx d 1.türeve bakalım. f ‘(x) 5a x 3bx c Bu ifade da : i Çözüm ma pozi – tiftir. Yani ar tan bir grafiğe sahiptir. Bu sebeple x eksenini sadece bir reel değerde kesebilir. O halde 1 tane reel kökü vardır. Diğer 4 kök, karmaşık sayıdır. 122
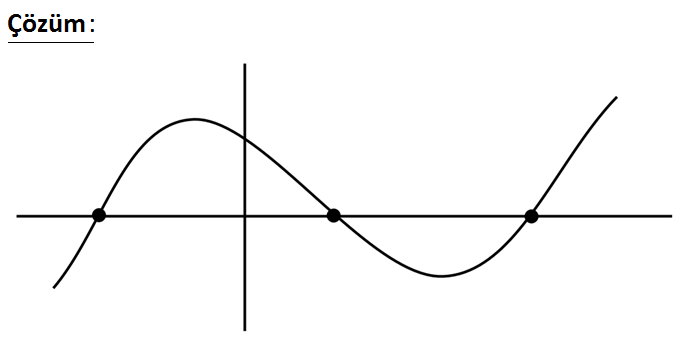
3 2 denkleminin üç farklı gerçek kökünün olmasını sağlayan ka 2 x ç farklı p 2x p ta 0 3 m sayıs ı var dır? A) 1 B) 2 C) 5 D) 8 E) 13 : Çözüm www.matematikkolay.net 3 farklı kökünün olabilmesi için yukarıdaki gibi bir grafiğe sahip olmalıdır. Bu grafikte; Bir adet yerel maksimum, bir adet yerel minimum noktası var dır. Bu noktada fonksiyonun değeri birinde pozitif, diğerinde negatiftir. Yani x a ve x b noktası ekstremum noktalar ise; f(a).f(b) 0 olmalıdır. f ‘(x) 0 2 2 x 4x 0 x 0 ve x 2 (Ekstremum) f(0).f(2) 0 olmalıdır. 16 p 8 p 0 3 8 p p 0 3 8 0, aralığında olmalıdır. 3 p 1,2 2 farklı p tam sayısı var dır. 124
2 f : ( , 3] [ 5, ) f(x) x ax b biçiminde tanımlanan bir f fonksiyonu bire bir ve örtendir. Buna gör e, a b toplamının alabileceği en büyük değer kaçtır? A) 13 B) 12 C) 11 D) 10 E) 9 www.matematikkolay.net Normalde bir parabol, birebir fonksiyon değildir. Tepe noktasına göre simetriktir. Soruda : veri Çözüm len, fonksiyonun birebir olabilmesi için fonksiyonun tanım kümesi parabolün bir tarafına ait olmalıdır. Bu soruda; Parabolün x değerlerini dan başlatarak vermeye başlıyoruz. Bu yüzden parabolün sağ ta 2 rafı olmamalıdır. Yani pozitif eğim olmamalı. f ‘ x 0 2x a 0 a’nın en büyük değerini elde etmek için Tanım kümesinin en büyük x 3 seçmeliyiz. elemanı 6 a 0 a en fazla 6 olabilir. a 6 olursa; x 6x b 2 polinomunun en küçük değeri 5 ise x 3 için bu polinom 5’i vermelidir. 3 6 3 b 5 9 18 b 5 b 4 olur. a b 6 4 10 buluruz. www.matematikkolay.net 167

