Soru Sor sayfası kullanılarak Türev konusu altında n.mertebeden türev, yüksek mertebeden türev ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
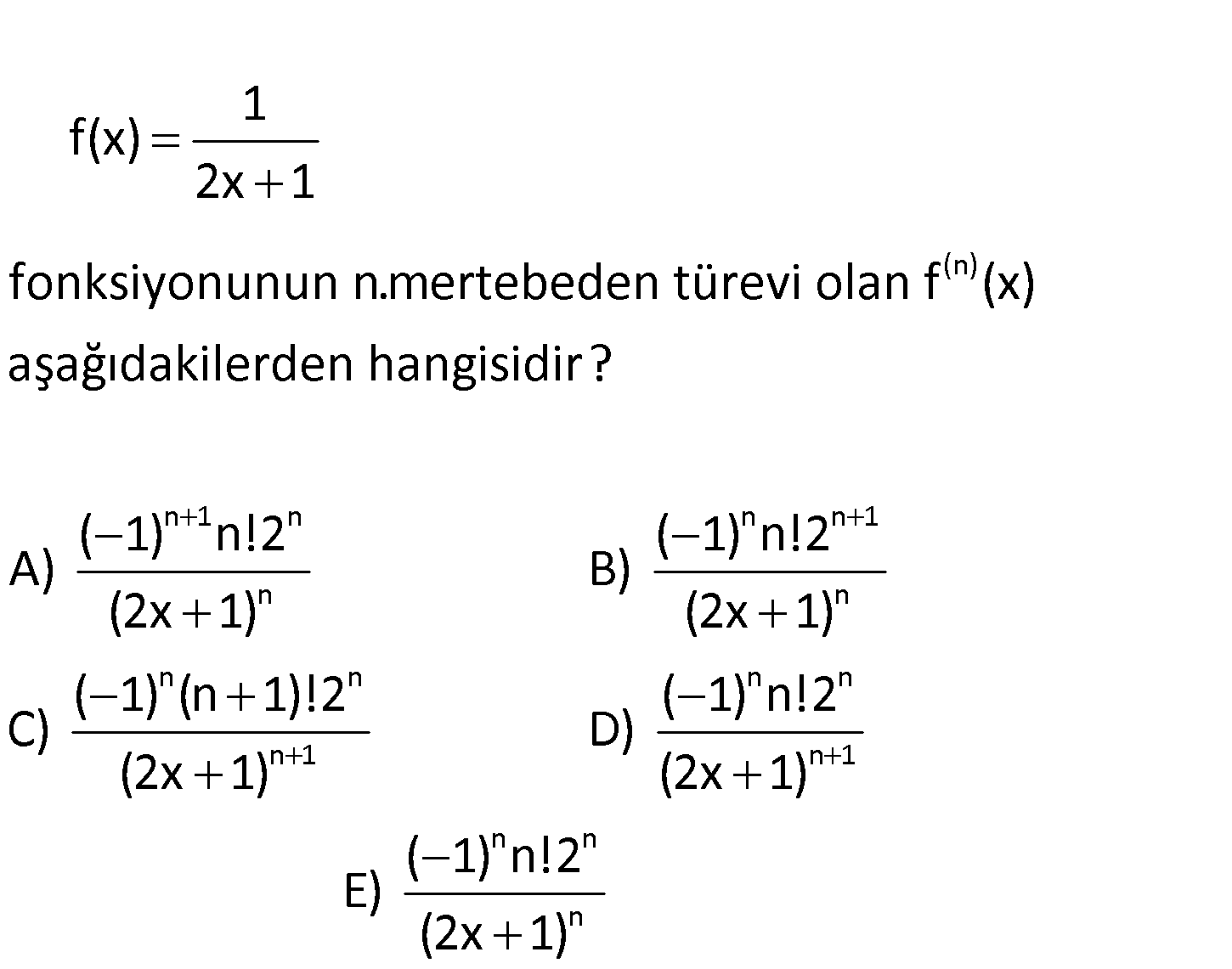

2.SORU

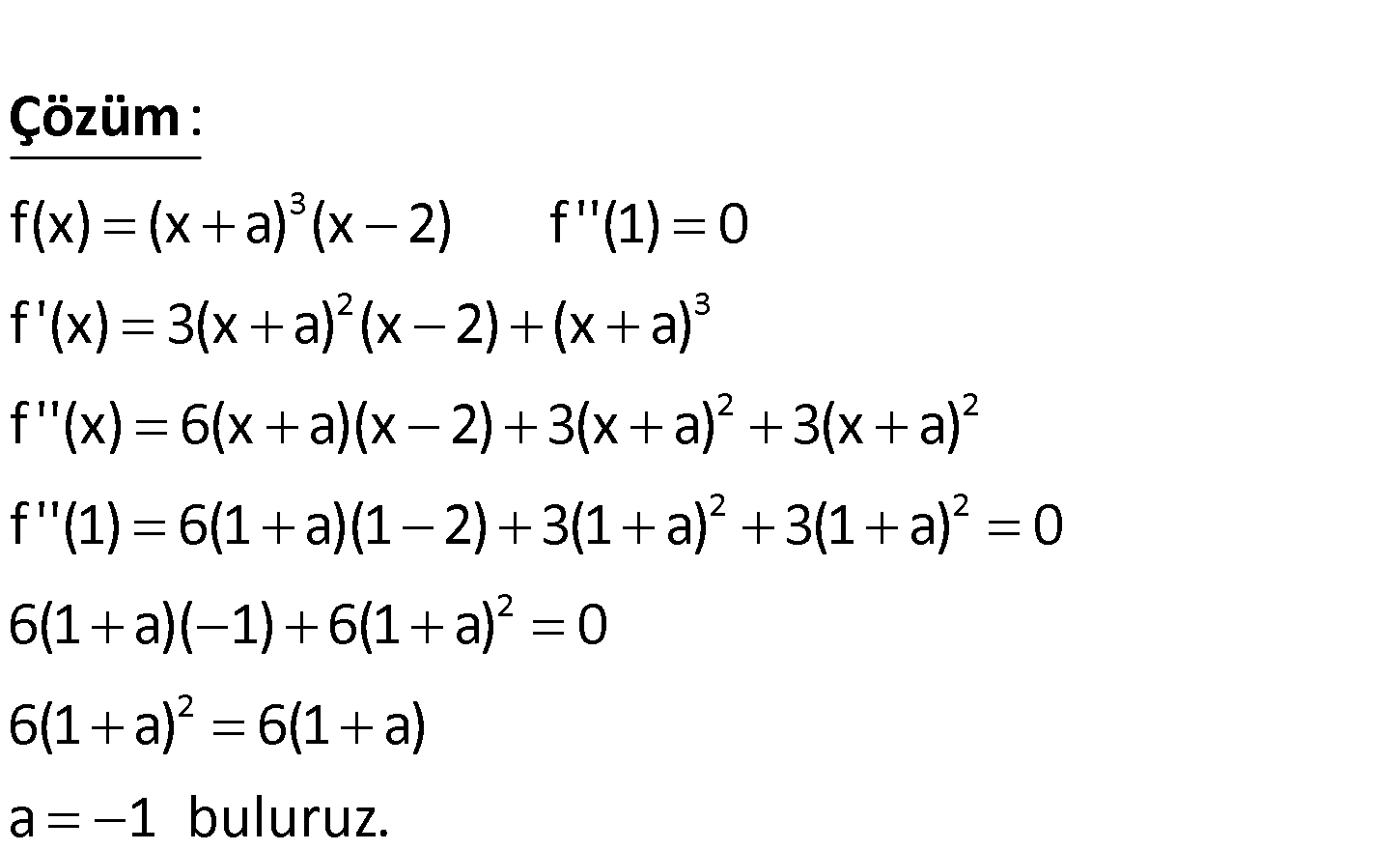
3.SORU


4.SORU
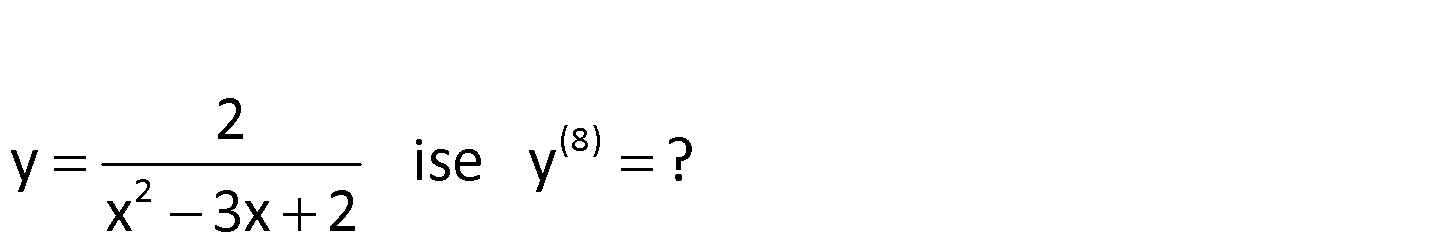
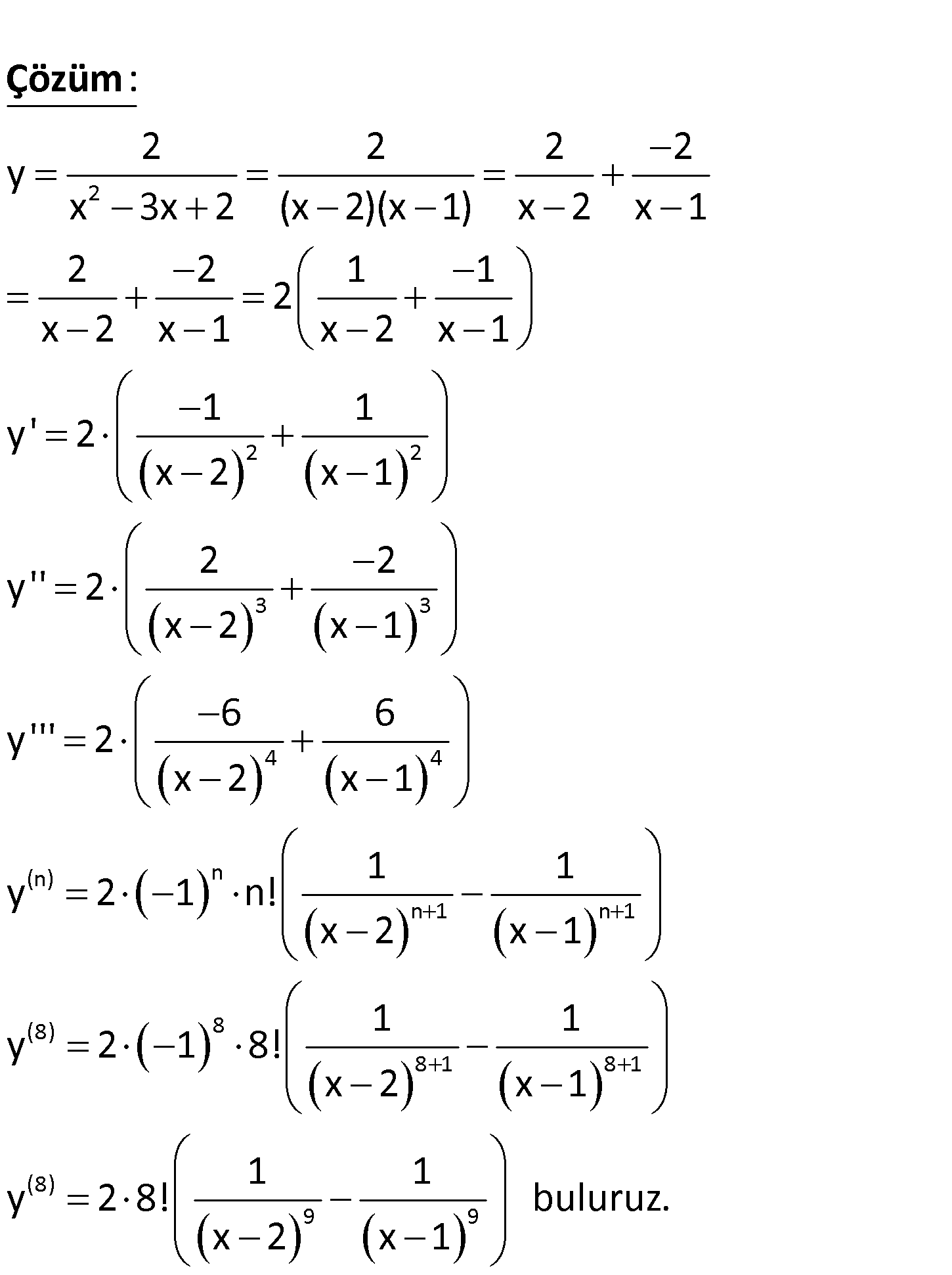
Burdan sonraki sorular, Fen Lisesi Müfredatı için geçerlidir.
5.SORU
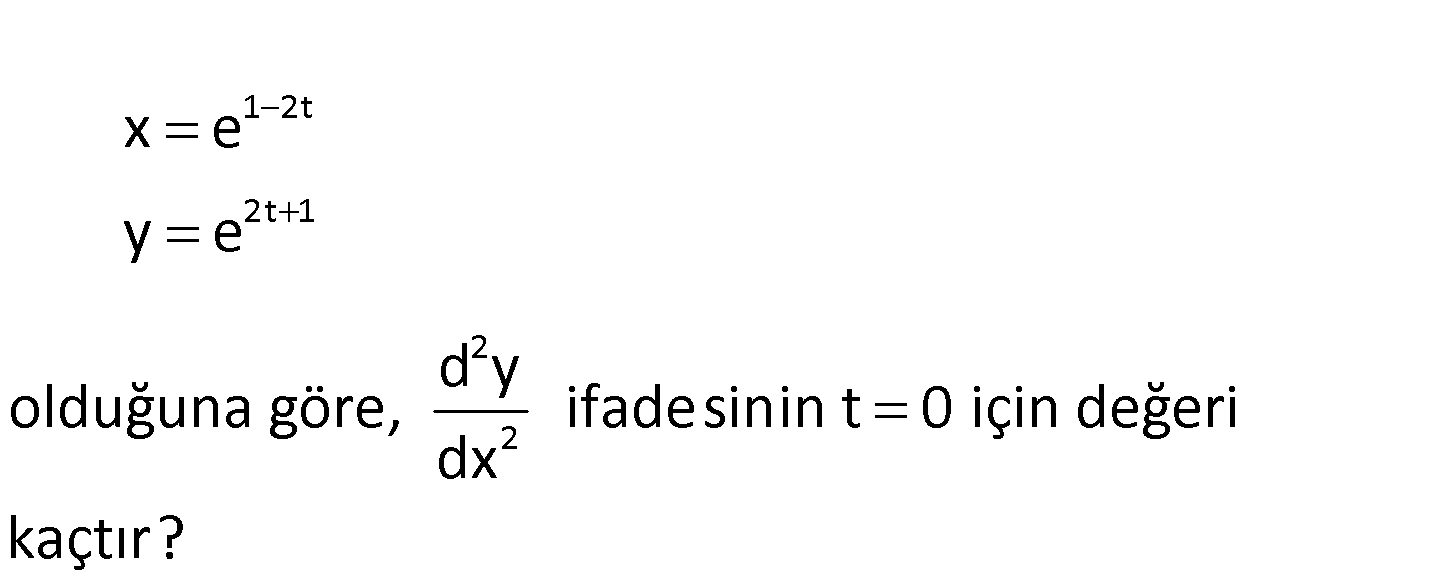
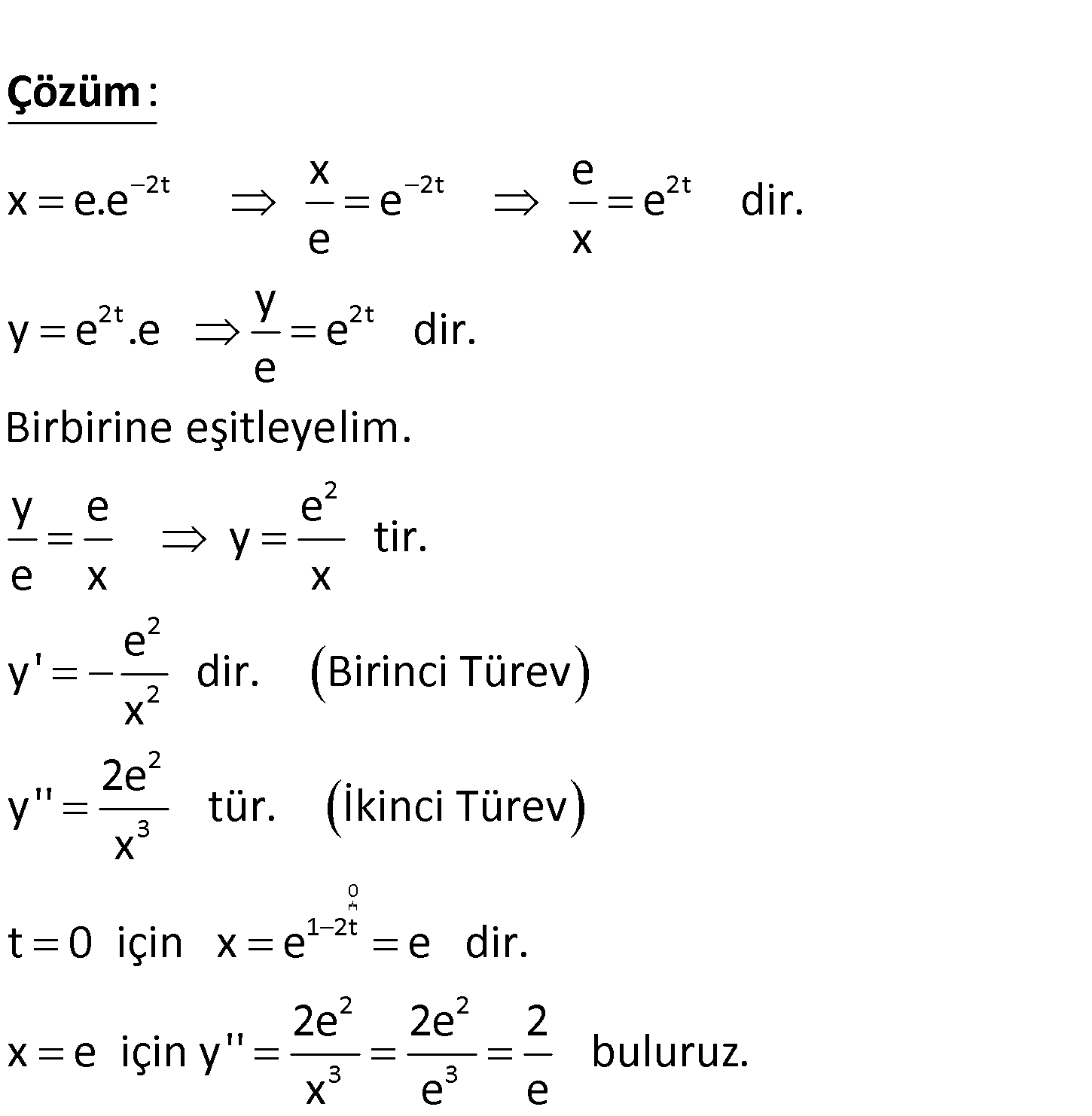
6.SORU

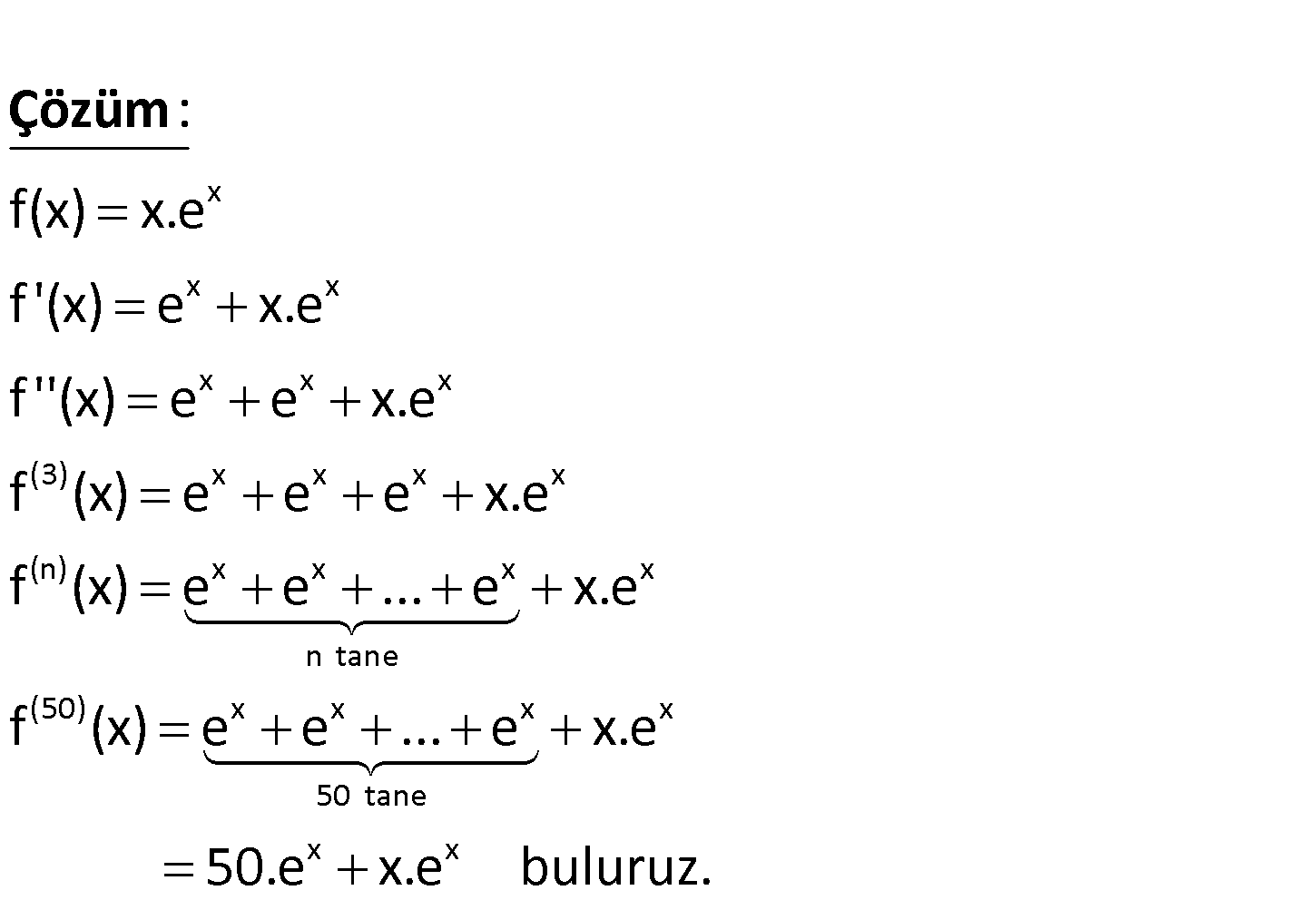
7.SORU


8.SORU
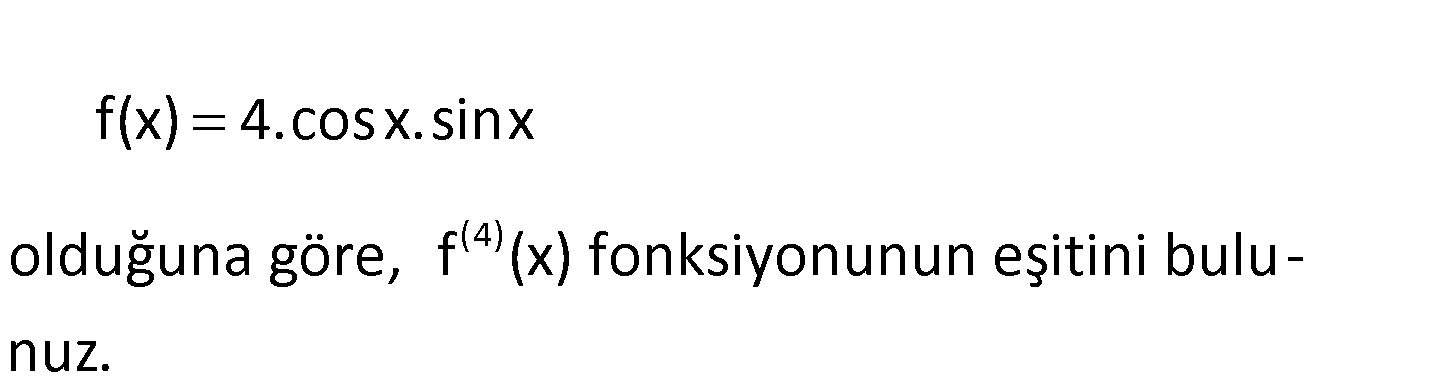

9.SORU
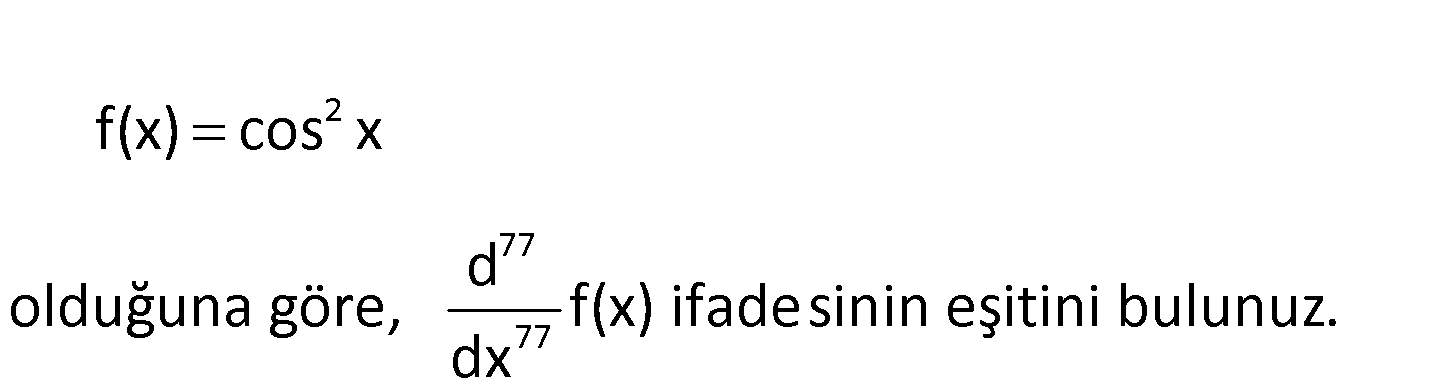

10.SORU
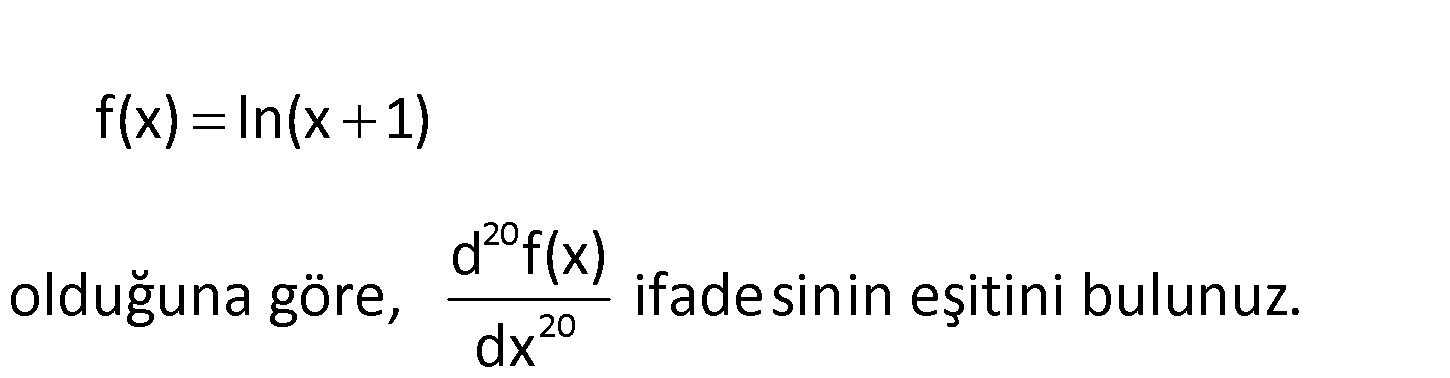
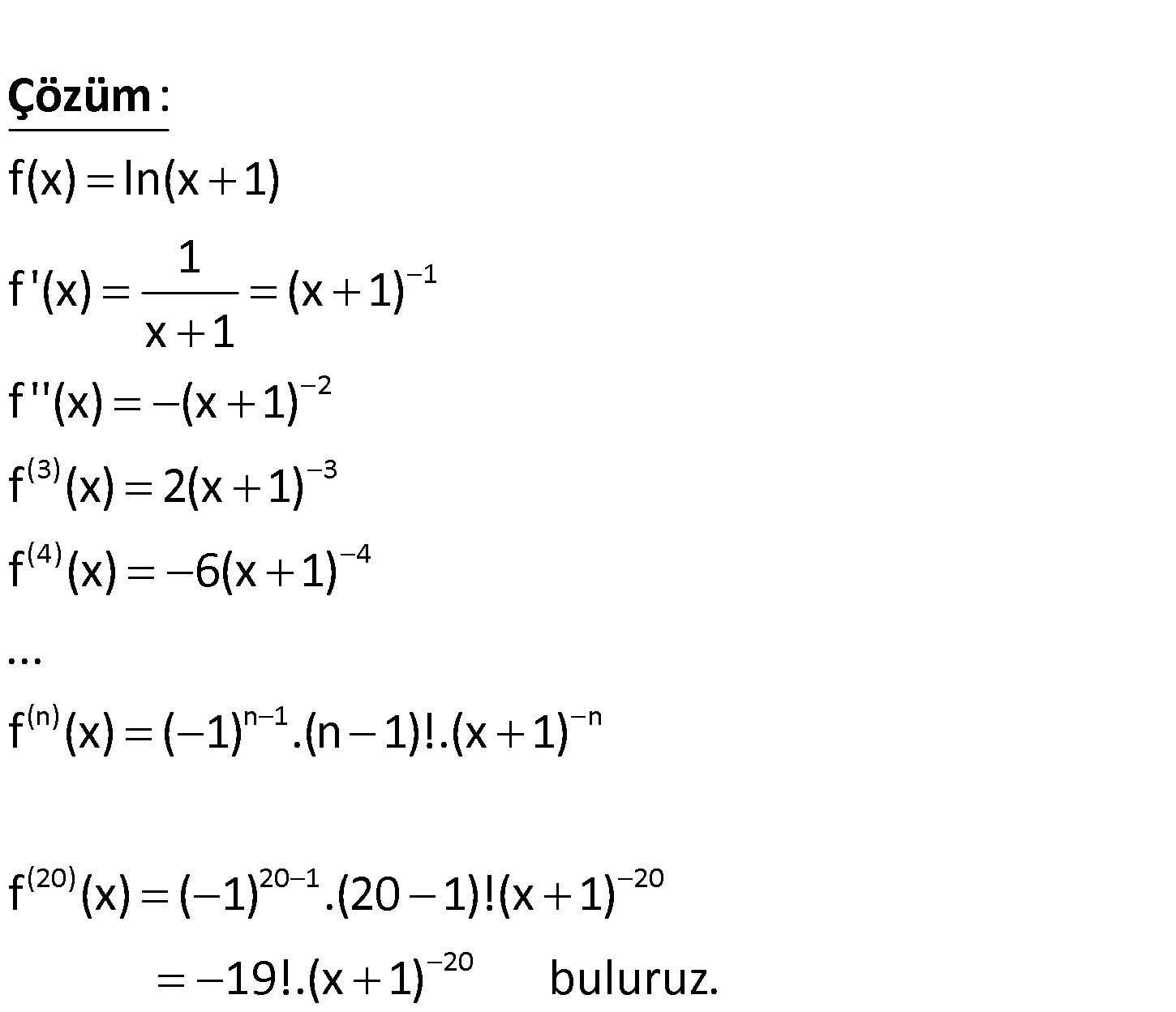
11.SORU
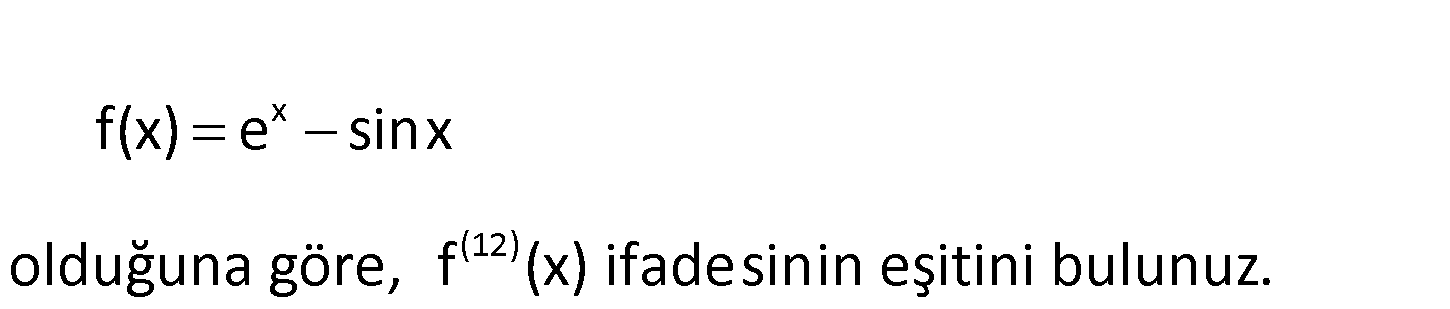

12.SORU

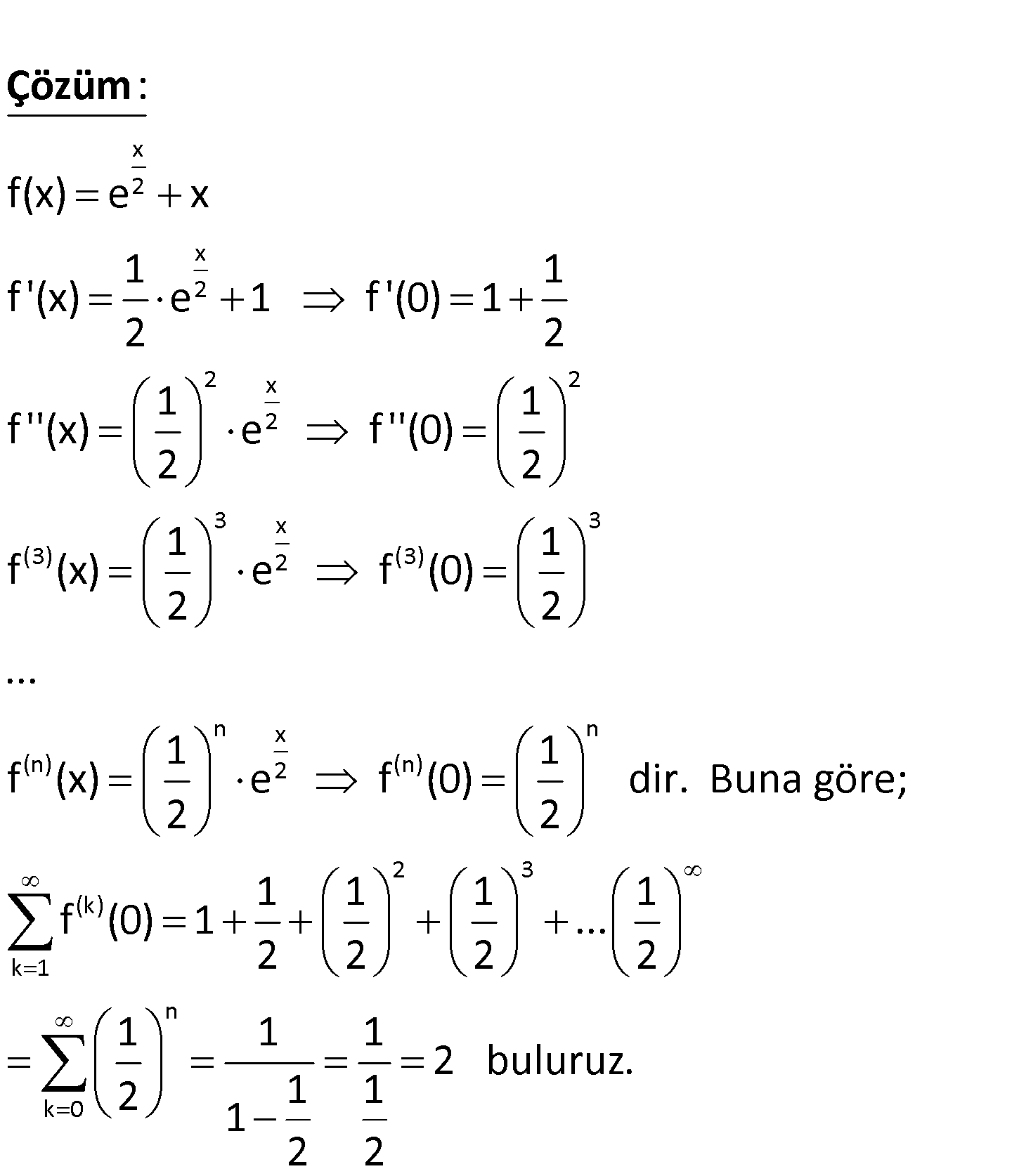
13.SORU
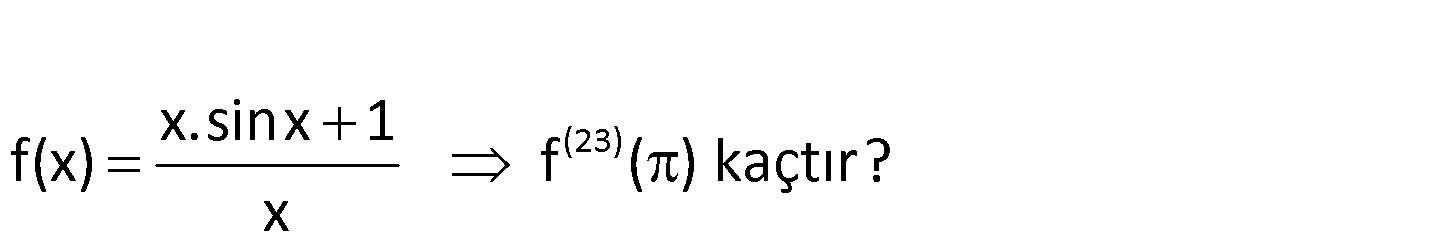

14.SORU
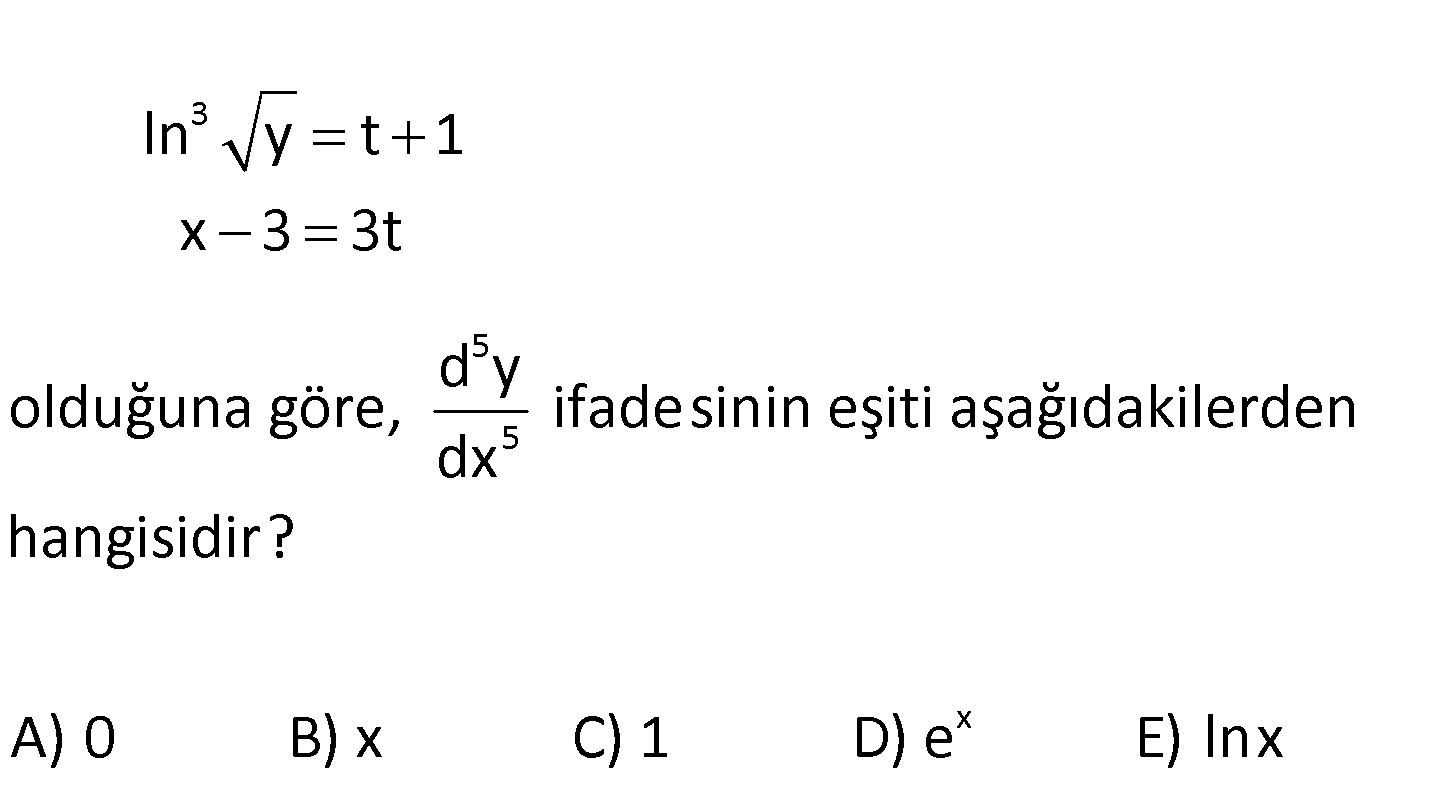

15.SORU

16.SORU
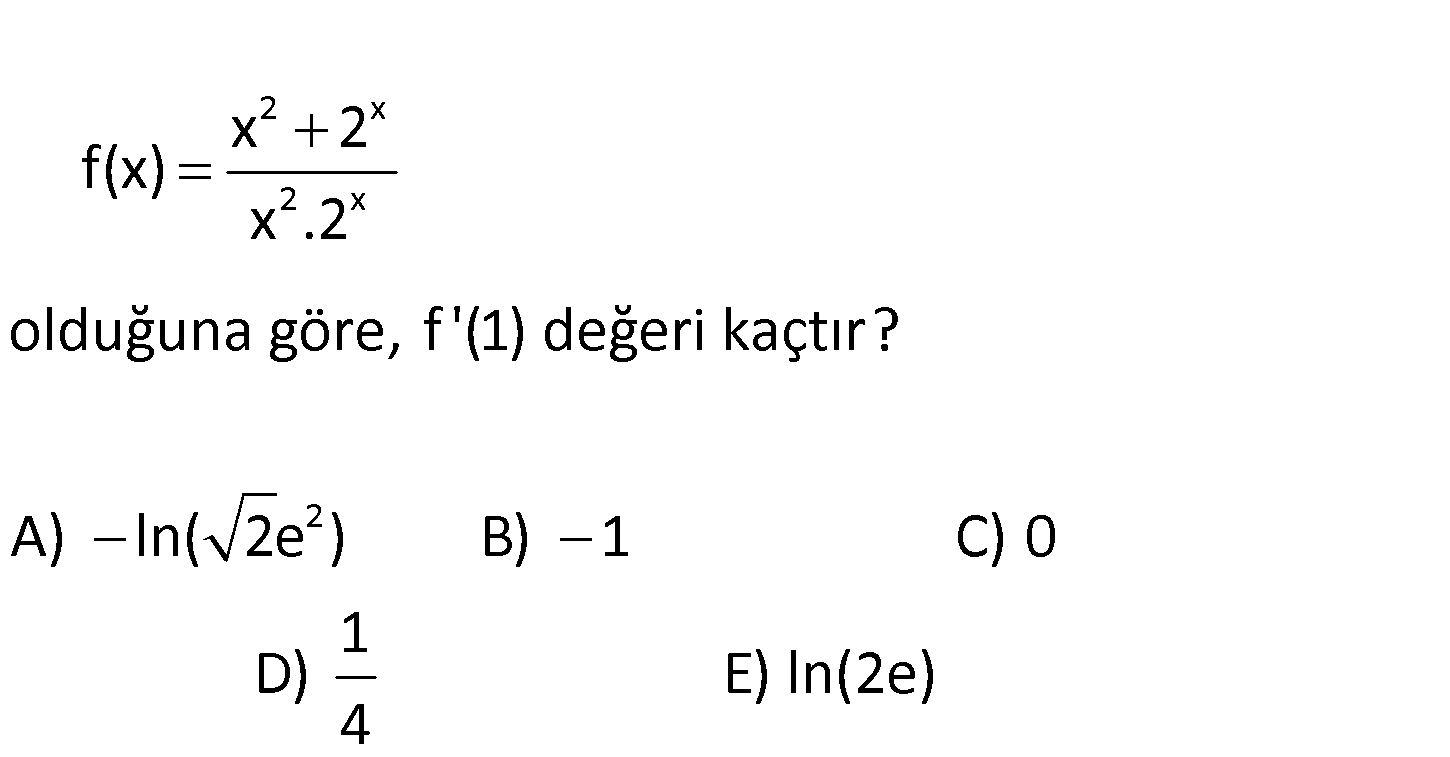
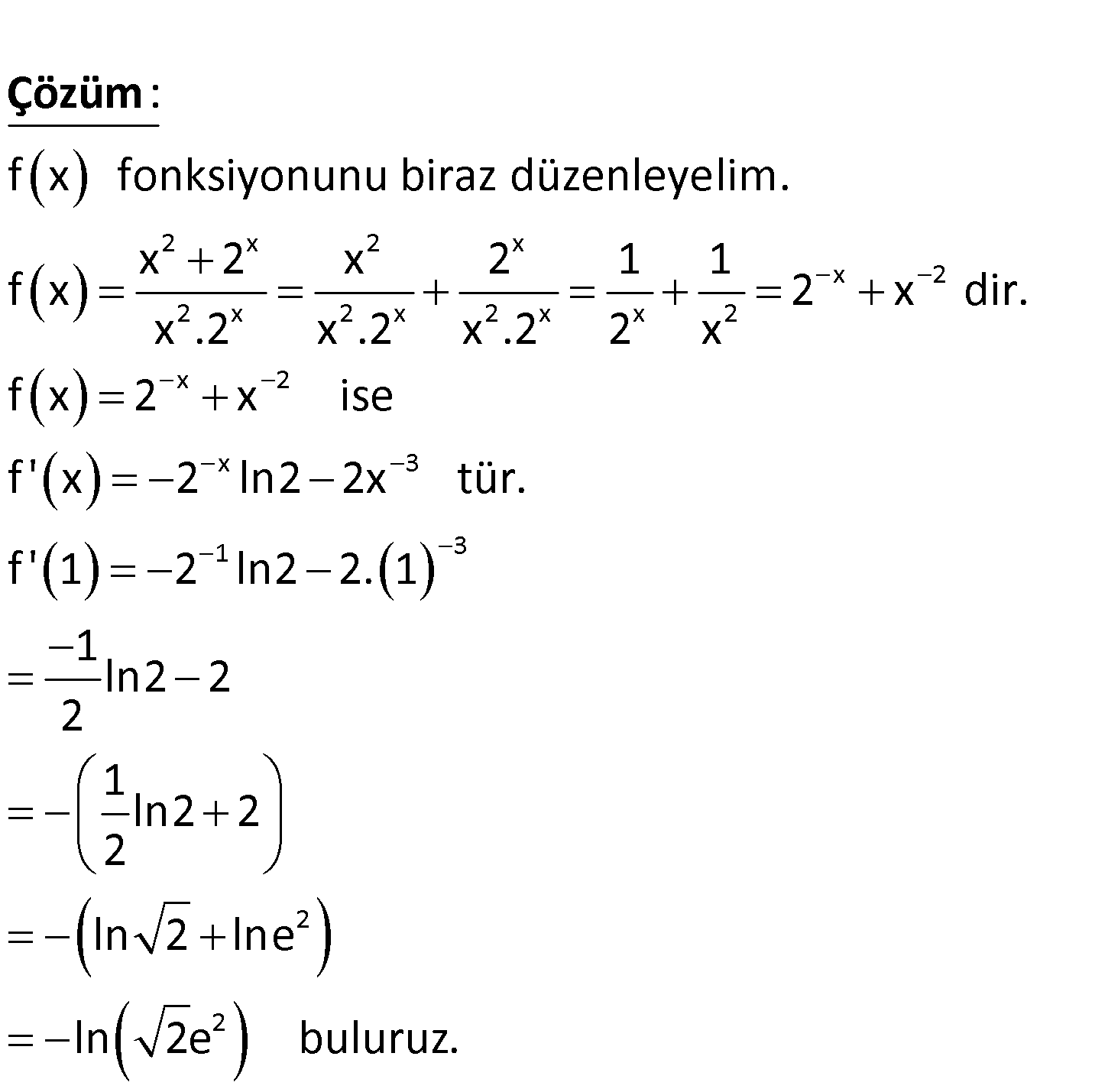
Diğer Soru Tipleri için Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
(n) n 1 f(x) 2x 1 fonksiyonunun n.mertebeden türevi olan f (x) aşağıdakilerden hangisidir? -1 A) 1 n n n 1 n n n n n n n 1 n 1 n n n n!2 ( 1) n!2 B) (2x 1) (2x 1) ( 1) (n 1)!2 ( 1) n!2 C) D) (2x 1) (2x 1) ( 1) n!2 E) (2x 1) www.matematikkolay.net 2 2 3 3 1 f(x) 2x 1 1.(2x 1)’ 1.2 1.türev (2x 1) (2x 1) 1.2.2.(2x 1)’ 1.2.2.2 1 2.türev (2x 1 x 1 : ) (2 ) Çözüm 2 3 2 3 4 4 4 5 n .2.2 (2x 1) 1.2.3.2 .(2x 1)’ 3!.2 3.türev (2x 1) (2x 1) 4!.2 4.türev (2x 1) …. Tek sayılı türevlerde negatif, çift sayılı türevlerde pozitif oluyor ( 1) olarak belirtebiliriz. Pay kısmında, kaçınc n n n 1 ı mertebeden türevdeysek, onun faktöriyeli ve 2 üzeri şeklinde o sayı var. Paydada ise mertebenin 1 fazlasının kuvveti şeklinde yazılıyor. Buna göre; ( 1) n! 2 n.türev şeklinde ifade edebili (2x 1) riz. 78
3 a sıfırdan farklı bir gerçek sayı olmak üzere, f(x) (x a) .(x 2) ve f ”(1) 0 olduğuna göre, a kaçtır? A) 2 B) 1 C) 1 D) 2 E) 3 www.matematikkolay.net 3 2 3 2 2 f(x) (x a) (x 2) f ”(1) 0 f ‘(x) 3(x a) (x 2) (x a) f ”(x) 6(x a)(x 2) 3(x a) 3 : (x a) f ‘ Çözüm 2 2 2 2 ‘(1) 6(1 a)(1 2) 3(1 a) 3(1 a) 0 6(1 a)( 1) 6(1 a) 0 6(1 a) 6(1 a) a 1 buluruz. 57
3 4 f(x) 3x(x 2) (x 2) fonksiyonunun ikinci mertebeden türevinin x 1 için değeri kaçtır? A) 12 B) 10 C) 9 D) 8 E) 7 3 4 3 3 ı 2 3 ı f(x) 3x(x 2) (x 2) f(x) (x 2) (3x x 2) f(x) (x 2) .(4x 2) f (x) 3.(x 2) .(4x 2) 4.(x 2) f : (x) Çözüm 2 ı 2 2 ıı 2 ıı 2 ıı (x 2) 3.(4x 2) 4.(x 2) f (x) (x 2) 12x 6 4x 8 (x 2) .(16x 14) f (x) 2.(x 2).(16x 14) 16.(x 2) f (1) 2.(1 2).(16.1 14) 16.(1 2) f (1) 2.2 16 12 bulunur. www.matematikkolay.net 81
-8 2 2 y ise y ? x 3x 2 www.matematikkolay.net 2 2 2 2 2 2 2 y x 3x 2 (x 2)(x 1) x 2 x 1 2 2 1 1 2 x 2 x 1 x 2 x 1 1 1 y’ 2 x 2 x 1 y” 2 : Çözüm 3 3 4 4 (n) n n 1 n 1 (8) 8 8 1 8 1 -8 9 9 2 2 x 2 x 1 6 6 y”’ 2 x 2 x 1 1 1 y 2 1 n! x 2 x 1 1 1 y 2
www.matematikkolay.net 1 2t 2t 1 2 2 d y olduğuna göre, if x e adesinin t 0 için değeri dx y e kaçtır? 2t 2t 2t 2t 2t x e x e.e e e dir. e x y y e .e e dir. e Birbirine eşitleyelim. y e e : x Çözüm 0 2 2 2 2 3 1 2t 2 2 3 3 e y tir. x e y’ dir. Birinci Türev x 2e y” tür. İkinci Türev x t 0 için x e e dir. 2e 2e 2 x e için y” buluruz. x e e 128
x -50 f(x) x.e olduğuna göre, f (x) ifadesinin eşitini bulunuz. www.matematikkolay.net x x x x x x (3) x x x x (n) x x x n tane f(x) x.e f ‘(x) e x.e f ”(x) e e x.e f (x) e e e x.e f (x) e e … e : Çözüm x (50) x x x x 50 tane x x x.e f (x) e e … e x.e 50.e x.e buluruz. 24
www.matematikkolay.net 2 f(x) 2sin x fonksiyonunun n.mertebe den türevi n edir? 2 3 -4 : f ‘(x) 4sinx.cosx 2sin2x f ”(x) 2.2cos2x 2 .cos2x f ”'(x) 4.2sin2x 2 sin2x f (x) 8.2cos2 x Çözüm (5) 5 n n n n n 16cos2x f (x) ( 16)( 2).sin2x 2 sin2x …. Türev her 4 adımda tekrarlanmaktadır. Buna göre; k bir sayma sayısı olmak üzere; n 4k ise f (x) 2 cos2x n 4k 1 ise f (x) 2 sin2x n 4k 2 ise f (x) n n n 2 cos2x n 4k 3 ise f (x) 2 sin2x 10
-4 f(x) 4.cosx.sinx olduğuna göre, f (x) fonksiyonunun eşitini bulunuz. f(x) 4.cosx.sinx f(x) 2.2cosx.sinx f(x) 2.sin2x f ‘(x) (2.sin2x)’ 2.2.cos2x 4cos2 : x Çözüm 2 3 4 f (x)= 8.sin2x f (x) 16cos2x f (x) 32sin2x buluruz. 23
2 77 77 f(x) cos x d olduğuna göre, f(x) ifadesinin eşitini bulunuz. dx 2 -3 -4 -5 f(x) cos x f ‘(x) 2cosx.sinx sin2x f ”(x) (sin2x)’ 2cos2x f (x) 4sin2x f (x) 8cos2x f (x) : Çözüm (77) 76 16sin2x … Her 4 türevde bir tekrarlanacaktır. 77. türevde 77 / 4 kalan 1 dir. Buna göre; f (x) 2 sin2x olacaktır. www.matematikkolay.net 25
20 20 f(x) ln(x 1) d f(x) olduğuna göre, ifadesinin eşitini bulunuz. dx 1 2 (3) 3 (4) 4 (n) f(x) ln(x 1) 1 f ‘(x) (x 1) x 1 f ”(x) (x 1) f (x) 2(x 1) f (x) 6(x 1) … f (x ( 1 : ) Çözüm n 1 n (20) 20 1 20 20 ) .(n 1)!.(x 1) f (x) ( 1) .(20 1)!(x 1) 19!.(x 1) buluruz. 26
x -12 f(x) e sinx olduğuna göre, f (x) ifadesinin eşitini bulunuz. www.matematikkolay.net x x x (3) x (4) x (5) x f(x) e sinx f ‘(x) e cosx f ”(x) e sinx f (x) e cosx f (x) e sinx f (x) e cosx : Çözüm (12) (4) x (tekrar ediyor) 4 türevde bir tekrar ediyor. 12 de 4’ün katı olduğundan; f (x) f (x) e sinx tir. 27
x 2 (n) (k) k 1 f(x) e x fonksiyonunun n.mertebeden türevi f (x) olmak üzere, f (0) i 2 fadesinin değeri kaçtır? A) 0 B) 1 C) 2 D) e E) e x 2 x 2 2 x 2 2 -3 f(x) e x 1 1 f ‘(x) e 1 f ‘(0) 1 2 2 1 1 f ”(x) e f ”(0) 2 2 1 f (x) 2 : Çözüm 3 x 3 2 (3) n x n (n) 2 (n) 2 3 (k) k 1 n k 0 1 e f (0) 2 … 1 1 f (x) e f (0) dir. Buna göre; 2 2 1 1 1 1 f (0) 1 … 2 2 2 2 1 1 1 2 buluruz. 2 1 1 1 2 2 www.matematikkolay.net 36
-23 x.sinx 1 f(x) f ( ) kaçtır? x 1 2 3 (3) 4 -4 x.sinx 1 1 f(x) sinx sinx x x x f ‘(x) cosx x f ”(x) sinx 2x f (x) cosx 6x f (x) sin : x Çözüm 4 1 n (n 1) (23) 23 (23 1) (23) 24 -23 24x Her 4 türevde bir, trigonometrik kısım tekrarlanıyor. x in türev
3 5 5 ln y t 1 x 3 3t d y olduğuna göre, ifadesinin eşiti aşağıdakilerden dx hangisidi x r? A) 0 B) x C) 1 D) e E) lnx 3 3 3 ln y t 1 t ln y 1 x 3 3t x 3 3(ln y 1) x 3 : Çözüm 3ln 3 y 3 3 3 x x 5 x 5 x ln y x lny y e dir. e ‘in tüm mertebelerden türevi kendisine eşittir. d y e bulunur. x 60
10 10 10 10 9 10 d (lnx) dx ifadesinin eşiti aşağıdakilerden hangisidir? 10! 9! 9! 9! A) B) C) D) E) x x x x 10 10! x www.matematikkolay.net 10 10 2 3 d (lnx) 10 kere türev almamız isteniyor. dx 1 1.türev x 1 2.türev x 01.Şub 3.türev x 4.tür : Çözüm 4 n 1 n 9 10 10 01.02.2003 ev x … (n 1)! n.türev ( 1) şeklinde yazabiliriz. x Buna göre; 9! 9! 10.türev ( 1) buluruz. x x 77
www.matematikkolay.net 2 2 x 2 x olduğuna göre, f ‘(1) değeri kaçtır? A) ln( 2e ) B) 1 C) 0 x 2 f(x) x .2 1 D) E) ln(2e) 4 2 x 2 x x 2 2 x 2 x 2 x x 2 x f x fonksiyonunu biraz düzenleyelim. x 2 x 2 1 1 f x 2 x dir. x .2 x .2 x .2 2 x f x : 2 Çözüm 2 x 3 1 3 2 2 x ise f ‘ x 2 ln2 2x tür. f ‘ 1 2 ln2 2. 1 1 ln2 2 2 1 ln2 2 2 ln 2 lne ln 2e buluruz. 136

