 Bu bölümde Köklü Sayılar (2.Bölüm) konusu ile ilgili 19 adet soru ve çözümleri bulunmaktadır. Sorular Latex formatında hazırlanarak görünüm iyileştirilmiştir. İyi Çalışmalar…
Bu bölümde Köklü Sayılar (2.Bölüm) konusu ile ilgili 19 adet soru ve çözümleri bulunmaktadır. Sorular Latex formatında hazırlanarak görünüm iyileştirilmiştir. İyi Çalışmalar…
Köklü Sayılar Test 2 Çözümlü Soruları pdf indir
Kitap Formatında Görmek için Tıkla
KÖKLÜ SAYILAR ÇÖZÜMLÜ SORULAR 2
SORU:1)
![]()
işleminin sonucu kaçtır?
![]()
ÇÖZÜM:
Toplama işlemini yapabilmek için ilk önce kesirlerin paydasını rasyonel yapalım. Bunun için köklü sayıları, kökten çıkaracak şekilde kendileri ile çarparak genişletelim;
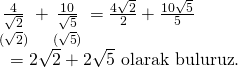
Doğru Cevap : A şıkkı
SORU:2)
![]()
işleminin sonucu kaçtır?
![]()
ÇÖZÜM:
Paydaların rasyonel hale getirilmesi gerekiyor. Bunun için paydadaki köklü sayılar eşlenikleri ile genişletilmelidir
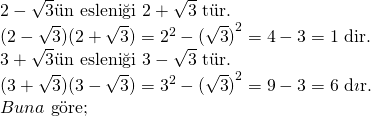
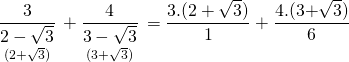
![]()
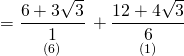
![]()
![]()
![]()
![]()
![]()
Doğru Cevap : C şıkkı
SORU:3)
![]()
işleminin sonucu kaçtır?
A) 1 B) 2 C) 3 D) 4 E) 5
ÇÖZÜM:
Kesirleri, köklü ifadelerin eşlenikleri ile genişleterek çözüme başlayalım;
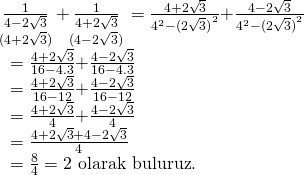
Doğru Cevap: B şıkkı
SORU:4)
![]()
ifadesinin eşiti aşağıdakilerden hangisidir?
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{l}\begin{array}{*{20}{l}} {A)\text{ }(\sqrt[4]{2}-1).(\sqrt{2}-1)\text{ }} & {B)\text{ }(\sqrt[4]{2}-1).(\sqrt{2}+1)} \\ {C)\text{ }(\sqrt[4]{2}+1).(\sqrt{2}+1)} & {D)\text{ }\frac{{(\sqrt[4]{2}+1).(\sqrt{2}-1)}}{8}} \end{array}\\\text{ E) }\frac{{(\sqrt[4]{2}+1).(\sqrt{2}-1)}}{2}\end{array}](https://www.matematikkolay.net/wp-content/ql-cache/quicklatex.com-c5d6126fade691d77da8ebbd73024f90_l3.png)
ÇÖZÜM:
Kesrin paydasını eşleniği ile genişleterek çözüme başlayalım,
![Rendered by QuickLaTeX.com \displaystyle \underset{{(\sqrt[4]{{32}}+2)}}{\mathop{{\frac{1}{{\sqrt[4]{{32}}-2}}}}}\,=\frac{{(\sqrt[4]{{32}}+2)}}{{{{{\left( {\sqrt[4]{{32}}} \right)}}^{2}}-{{2}^{2}}}}=\frac{{\sqrt[4]{{32}}+2}}{{\sqrt{{32}}-4}}\text{ }](https://www.matematikkolay.net/wp-content/ql-cache/quicklatex.com-69be5ee833445f81d3645e9b50d830fe_l3.png)
Kesri tekrar paydanın eşleniği ile genişletelim,
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{l}=\frac{{(\sqrt[4]{{{{2}^{4}}.2}}+2)(\sqrt{{{{4}^{2}}.2}}-4)}}{{16}}\text{ }\\\text{ }=\frac{{(2.\sqrt[4]{2}+2)(4.\sqrt{2}-4)}}{{16}}\text{ (Ortak parantez)}\\\text{ }=\frac{{2.(\sqrt[4]{2}+1).4(\sqrt{2}-1)}}{{16}}\\\text{ }=\frac{{8.(\sqrt[4]{2}+1).(\sqrt{2}-1)}}{{16}}\\\text{ }=\frac{{(\sqrt[4]{2}+1).(\sqrt{2}-1)}}{2}\end{array}](https://www.matematikkolay.net/wp-content/ql-cache/quicklatex.com-258f0fb88579b7afc9fffecad543f247_l3.png)
Köklü ifadelerin içerisinden değerleri dışarıya çıkarmaya çalışalım,
Doğru Cevap : E şıkkı
SORU:5)
![]()
işleminin sonucu kaçtır?
![]()
ÇÖZÜM:
![]()
ifadesinin payında yer alan köklü ifadeleri iki iki ortak paranteze alalım,
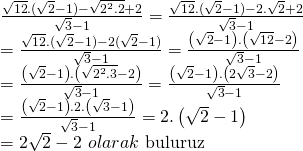
Doğru Cevap : D şıkkı
SORU:6)
![]()
işleminin sonucu kaçtır?
![]()
ÇÖZÜM:
Köklü ifadelerin dereceleri aynı olduğundan çarpma işlemini kök içerisinde yapabiliriz.
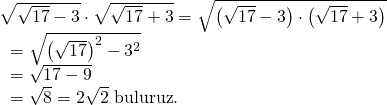
Doğru Cevap : E şıkkı
SORU:7)
![]()
ifadesinin eşiti aşagıdakilerden hangisidir?
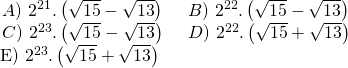
ÇÖZÜM:
Üssü 23 olan parantezden bir çarpan ayırarak diğer parantezle üssün aynı olmasını sağlayalım,
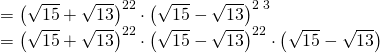
Üsleri aynı olan parantezlerin içini kendi aralarında çarpabiliriz.Buna göre;
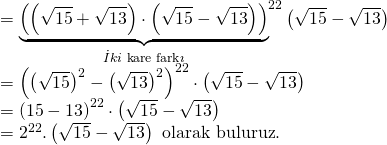
Doğru Cevap: B şıkkı
SORU:8)
![]()
işleminin sonucu kaçtır?
A) 1 B) 2 C) 3 D) 4 E) 5
ÇÖZÜM:
![]()
Bu eşitliği kullanabilmek için ![]() şeklinde yazalım,
şeklinde yazalım,
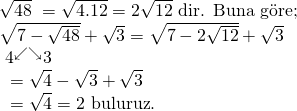
Doğru Cevap : B şıkkı
SORU:9)
![]()
işleminin sonucu kaçtır?
![]()
ÇÖZÜM:

Doğru Cevap: A şıkkı
SORU:10)
![]()
işleminin sonucu kaçtır?
![]()
ÇÖZÜM:
Sorunun çözümünde ![]() biçiminden yararlanmak için verilen ifadeyi
biçiminden yararlanmak için verilen ifadeyi ![]() ile çarpıp
ile çarpıp
![]() ye bölelim,
ye bölelim,
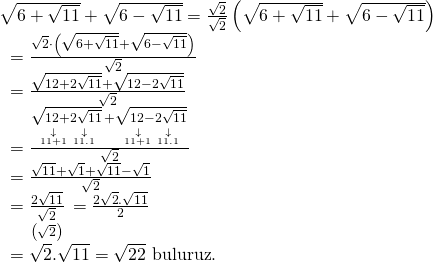
Doğru Cevap : E şıkkı
SORU:11)
![]()
ifadesi aşağıdakilerden hangisine eşittir?
![]()
ÇÖZÜM:
Köklü ifadede içerisindeki tüm değerleri en içteki kökün içerisine aktarmaya çalışalım.
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{l}\underset{{\downarrow {{3}^{3}}\nearrow \text{ }}}{\mathop{{\sqrt[4]{{3\sqrt[3]{{9\sqrt{{27}}}}}}}}}\,=\underset{{\text{ }\overset{\downarrow }{\mathop{{{{3}^{{3\ +\ 2}}}}}}\,\text{ }}}{\mathop{{\sqrt[4]{{\sqrt[3]{{{{3}^{3}}9\sqrt{{27}}}}}}}}}\,=\underset{{\text{ }\downarrow \ 3{{\ }^{{10}}}\nearrow \text{ }}}{\mathop{{\sqrt[4]{{\sqrt[3]{{{{3}^{5}}\sqrt{{27}}}}}}}}}\,\\\sqrt[4]{{\sqrt[3]{{\sqrt{{{{3}^{{10}}}27}}}}}}=\sqrt[4]{{\sqrt[3]{{\sqrt{{{{3}^{{10}}}{{3}^{3}}}}}}}}=\underset{\begin{smallmatrix} K\ddot{o}k\text{ derecelerini} \\ \text{carpal }\!\!\imath\!\!\text{ m}\text{.} \end{smallmatrix}}{\mathop{{\sqrt[4]{{\sqrt[3]{{\sqrt{{{{3}^{{1\ 3}}}}}}}}}}}}\,\\\text{ }=\sqrt[{4.3.2}]{{{{3}^{{1\ 3}}}}}=\sqrt[{2\ 4}]{{{{3}^{{1\ 3}}}}}\text{ buluruz}\end{array}](https://www.matematikkolay.net/wp-content/ql-cache/quicklatex.com-6de1a4731f10c44b4913c2092f711a52_l3.png)
Doğru Cevap : D şıkkı
SORU:12)
![]()
işleminin sonucu kaçtır?
A) 4 B) 6 C) 9 D) 12 E) 36
ÇÖZÜM:
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{l}\sqrt[3]{{36.\sqrt[3]{{36.\sqrt[3]{{36...}}}}}}\text{ }ifade\sin in\text{ }sonucuna\text{ }x\text{ }diye\lim ;\\\underset{{\overset{{\text{ }\Downarrow }}{\mathop{{\text{ }buraya\text{ }da\text{ }x\text{ }diyebiliriz}}}\,}}{\mathop{{\sqrt[3]{{36.\underline{{\sqrt[3]{{36.\sqrt[3]{{36...}}}}}}}}}}}\,=x\text{ }Buna\text{ }g\ddot{o}re\text{ }denklemi\text{ c}\ddot{o}ze\lim ,\\\text{ }\sqrt[3]{{36.x}}=x\\{{\left( {\sqrt[3]{{36.x}}} \right)}^{3}}={{x}^{3}}\\\text{ }36x={{x}^{3}}\\\text{ }36={{x}^{2}}\\\text{ }x=6\text{ }bulunur.\end{array}](https://www.matematikkolay.net/wp-content/ql-cache/quicklatex.com-6ea388055f8214547ceba464e4b501f0_l3.png)
(Not : Böyle iç içe sonsuz çarpımlarda kökün derecesi 1 azaltıp sonuca hemen gidebiliriz.
![]()
Doğru Cevap : B şıkkı
SORU:13)
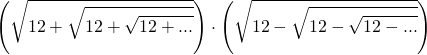
işleminin sonucu kaçtır?
A) 3 B) 4 C) 7 D) 12 E) 144
ÇÖZÜM:
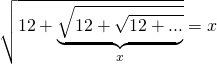
şeklinde denklemi yazıp çözüme gidebiliriz. Ancak bu tarz sonsuz toplam ve çıkarmalarda ezbersel kolay bir yöntem var. Eğer içerdeki sayı ardışık iki terimin çarpımı şeklinde yazılabiliyorsa toplamın sonucu büyük terime, çıkarmanın
sonucu küçük terime eşittir. Yani;
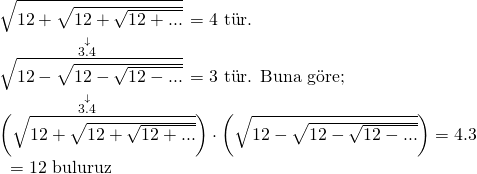
Doğru Cevap : D şıkkı
SORU:14)
![]()
işleminin sonucu kaçtır?
A) 1 B) 2 C) 3 D) 4 E) 5
ÇÖZÜM:
Kök içerisindeki ifadeyi tam kare şeklinde ifade edebiliriz.
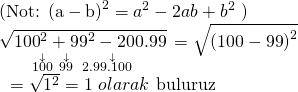
Doğru Cevap : A şıkkı
SORU:15)
![]()
işleminin sonucu kaçtır?
A) 100 B) 120 C) 125 D) 130 E) 150
ÇÖZÜM:
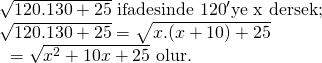
Bu ifadeye dikkatli bakarsak tam kare bir ifade olduğunu görebiliriz;
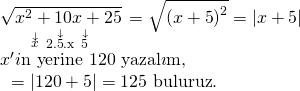
Doğru Cevap : C şıkkı
SORU:16)
![]()
işleminin sonucu kaçtır?
A) 2 B) 3 C) 4 D) 5 E) 6
ÇÖZÜM:
![]()
ifadesini rahat çözebilmek için çarpılan sayılardan birine x diyelim, Mesela 1997= x olsun. Buna göre;
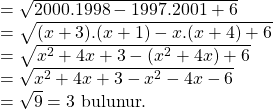
Doğru Cevap : B şıkkı
SORU:17)
Aşağıda verilen irrasyonel sayılardan hangisinin yaklaşık değeri bilinirse ![]() sayısının yaklaşık değeri bulunabilir?
sayısının yaklaşık değeri bulunabilir?
![]()
ÇÖZÜM:
![]() köklü ifadenin içindeki sayıyı olabildiğince kökün dışına çıkaralım. Bunun için sayıyı çarpanlarına ayıralım.
köklü ifadenin içindeki sayıyı olabildiğince kökün dışına çıkaralım. Bunun için sayıyı çarpanlarına ayıralım.
![]() tür. Eğeri
tür. Eğeri ![]() ‘ün yaklaşık değeri bilinirse köklü ifadenin değeri bulunabilir.
‘ün yaklaşık değeri bilinirse köklü ifadenin değeri bulunabilir.
Doğru Cevap : B şıkkı
SORU:18)
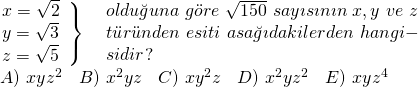
ÇÖZÜM:
![]() sayısını asal çarpanlarına ayıralım;
sayısını asal çarpanlarına ayıralım;
![]()
Şimdi x,y ve z değerlerini yazalım;
![]() olarak buluruz.
olarak buluruz.
Doğru Cevap : A şıkkı
SORU:19)
![]()
olduğuna göre ![]() ifadesinin değeri kaçtır?
ifadesinin değeri kaçtır?
A) 1 B) 2 C) 3 D) 4 E) 5
ÇÖZÜM:
Soruda istenen ifade, bir değere eşit olsun,
![]() olsun,
olsun,
Soruda bize ![]() ‘ in 5’ e eşit olduğu verilmiş. Bu iki denklemi taraf tarafa çarpalım;
‘ in 5’ e eşit olduğu verilmiş. Bu iki denklemi taraf tarafa çarpalım;
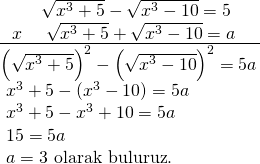
Doğru Cevap : C şıkkı
Köklü Sayılar Test 2 Çözümlü Soruları pdf indir
Kitap Formatında Görmek için Tıkla


Bir matematikci olarak tavsiye ederim. Gayet guzel bi site.
çok güzel sorular matematik projemde yardımcı oldun sayısalcıyım ve beğendim
16. sorunun cevabi dogru fakat cozumu yanlis.Duzeltilirse faydali sorular
Uyarınız için teşekkürler. Hata düzeltildi.