Ağırlık Merkezi ve Alan

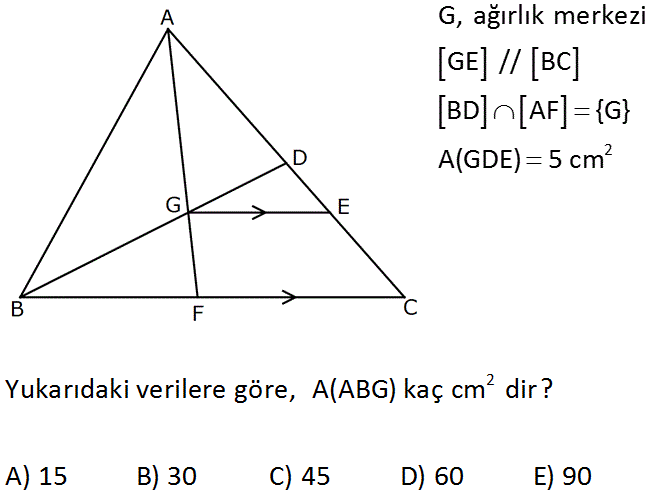
2 G, ağırlık merkezi GE // BC BD AF {G} A(GDE) 5 cm  www.matematikkolay.net 2 Yukarıdaki verilere göre, A(ABG) kaç cm dir? A) 15 B) 30 C) 45 D) 60 E) 90 : Çözüm Ağırlık merkezi, kenarortayı köşeden kenara 2’ye 1 oranında böler. Yani; GD k ise BG 2k olur. GE / /BC verilmiş. DGE üçgeni ile DBC üçgenleri arasındaki benzerlik vardır. GD k 1 Benzerlik oranı BD 3k 3 2 tür. 1 Alanları oranı da bu oranın karesidir. 9 5 1 A BDC 45 cm dir. A BDC 9 BD doğrusu kenarortay olduğundan AD DC dir. Bu sebeple A ABD A BDC 45 tir. ABG üçgeni ile AGD üçgeni 45’lik alanı tabanlar   2 ı oranında paylaşırlar. 2k ve k A ABG 30 , A AGD 15 olur. Cevap: A ABG 30 cm dir.  www.matematikkolay.net 67
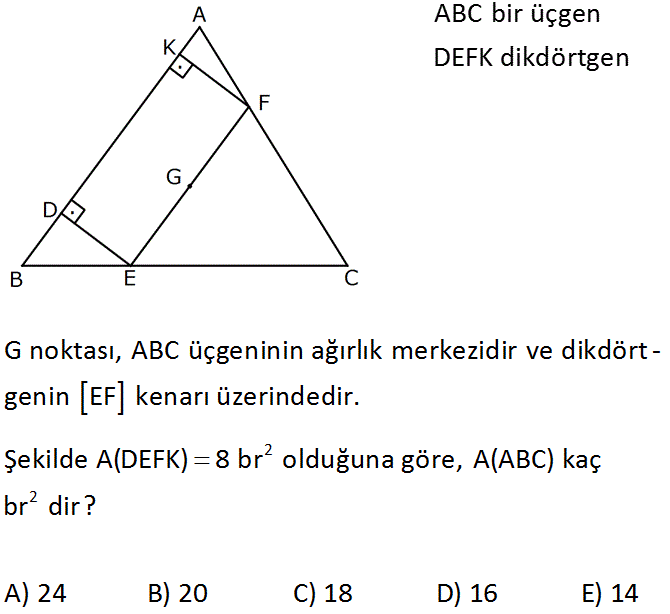
ABC bir üçgen DEFK dikdörtgen2 2 G noktası, ABC üçgeninin ağırlık merkezidir ve dikdört – genin EF kenarı üzerindedir. Şekilde A(DEFK) 8 br olduğuna göre, A(ABC) kaç br dir? A) 24 B) 20 C) 18 D) 16 E) 14 : Çözüm www.matematikkolay.net Ağırlık merkezi, bir kenarortayı köşeden kenara 2’ye 1 oranında böler. DEFK bir dikdörtgen olduğundan, C’den P’ye yükseklik indirisek, kenarortay gibi 2’ye 1 oranında parçalanır. PR k ise RC 2k olur. 2 A BDE A ise A ERC 4A olur. k 1 Benzerlik oranı dır. Alanları oranı olmalı. 2k 2 Aynı şekilde; A AKF B ise A FGC 4B dir. A FEC 4A 4B olur. 2k FEC üçgeni ile ABC üçgeni arasında oranı var 3k                . 4 Alanları oranı da olmalıdır. 9 A FEC 4A 4B ise A ABC 9A 9B olur. A DEFK A ABC A FEC A BDE A AKF 8 9A 9B 4A 4B A B 8 4A 4B 2 A B dir. A ABC 9A 9B 18 buluruz.              68