Soru Sor sayfası kullanılarak Üçgende Alan konusu altında Alanların eşitliği, Taban kaydırma, Yükseklik kaydırma ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
2.SORU
3.SORU
4.SORU
5.SORU
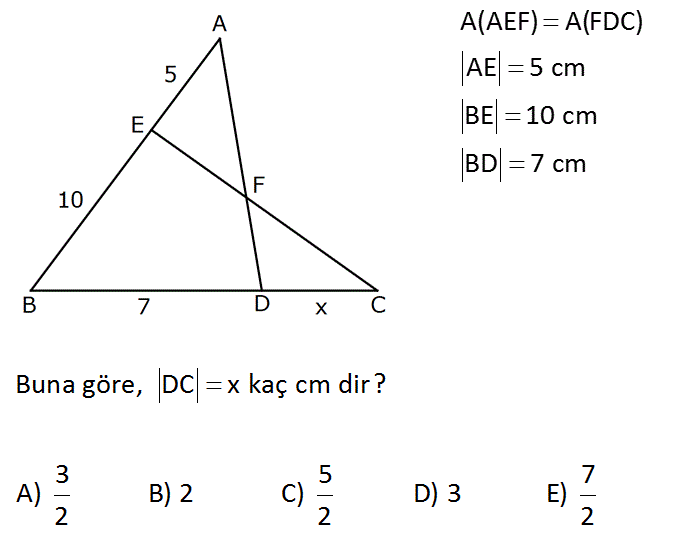

6.SORU


Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
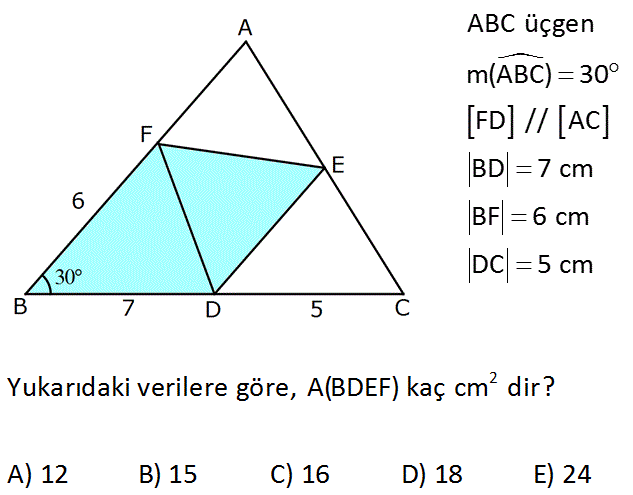
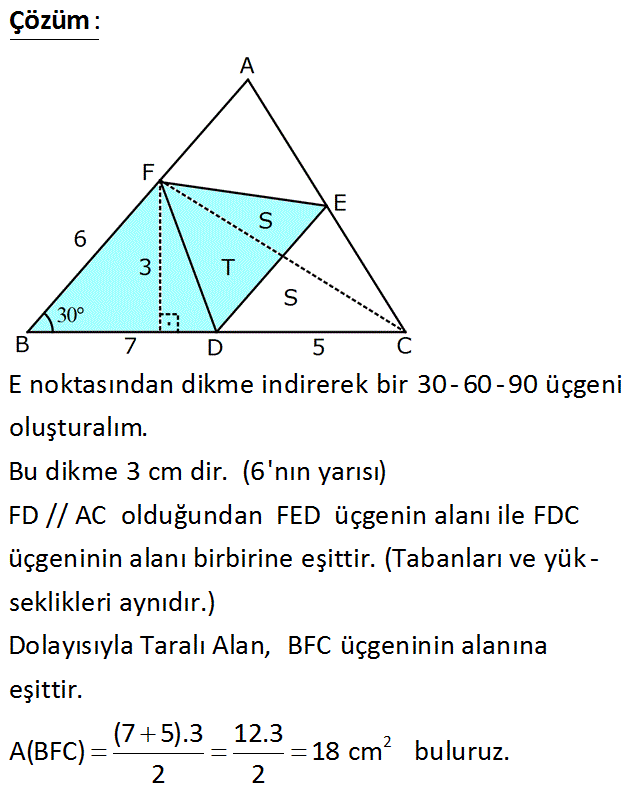
www.matematikkolay.net ABC ü çgen m(ABC) 30 FD // AC BD 7 cm BF 6 cm DC 5 cm 2 Yukarıdaki verilere göre, A(BDEF) kaç cm dir? A) 12 B) 15 C) 16 D) 18 E) 24 : Çözüm E noktasından dikme indirerek bir 30 – 60 – 90 üçgeni oluşturalım. Bu dikme 3 cm dir. (6’nın yarısı) FD // AC olduğundan FED üçgenin alanı ile FDC üçgeninin alanı birbirine eşittir. (Tabanları ve yük – sekl 2 ikleri aynıdır.) Dolayısıyla Taralı Alan, BFC üçgeninin alanına eşittir. (7 5).3 12.3 A(BFC) 18 cm buluruz. 2 2 www.matematikkolay.net 24
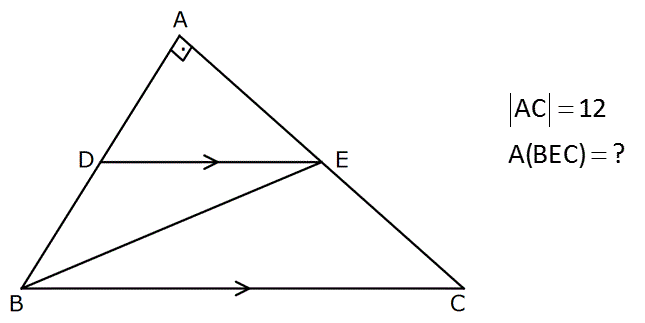
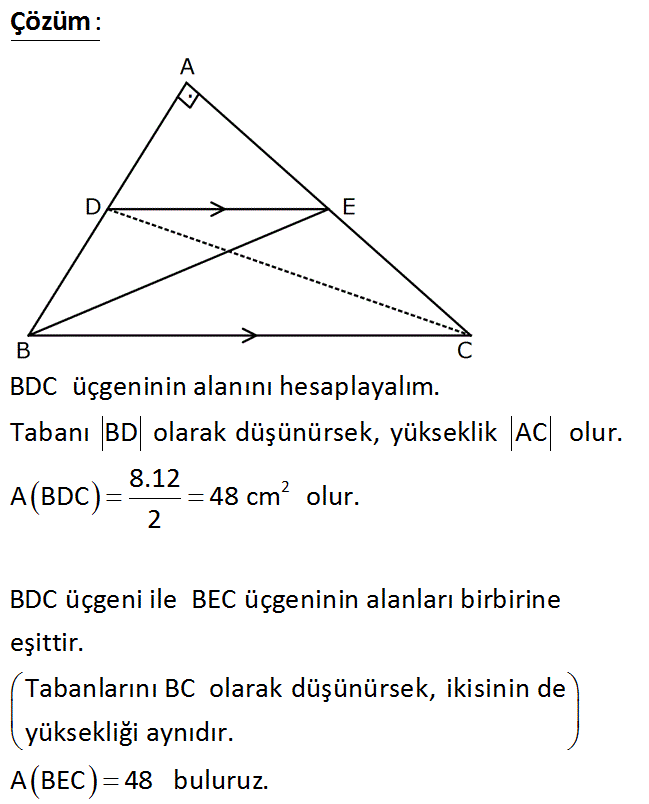
AC 12 A(BEC) ? Çözüm: www.matematikkolay.net 2 BDC üçgeninin alanını hesaplayalım. Tabanı BD olarak düşünürsek, yükseklik AC olur. 08.Ara A BDC 48 cm olur. 2 BDC üçgeni ile BEC üçgeninin alanları birbirine eşittir. Tabanlarını BC olarak düşünürsek, ikisinin de yüksekliği aynıdır. A BEC 48 buluruz. 55
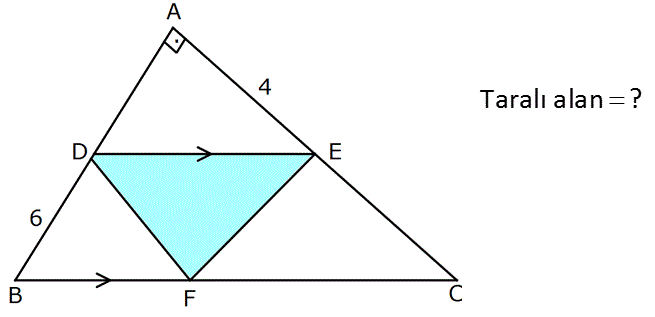
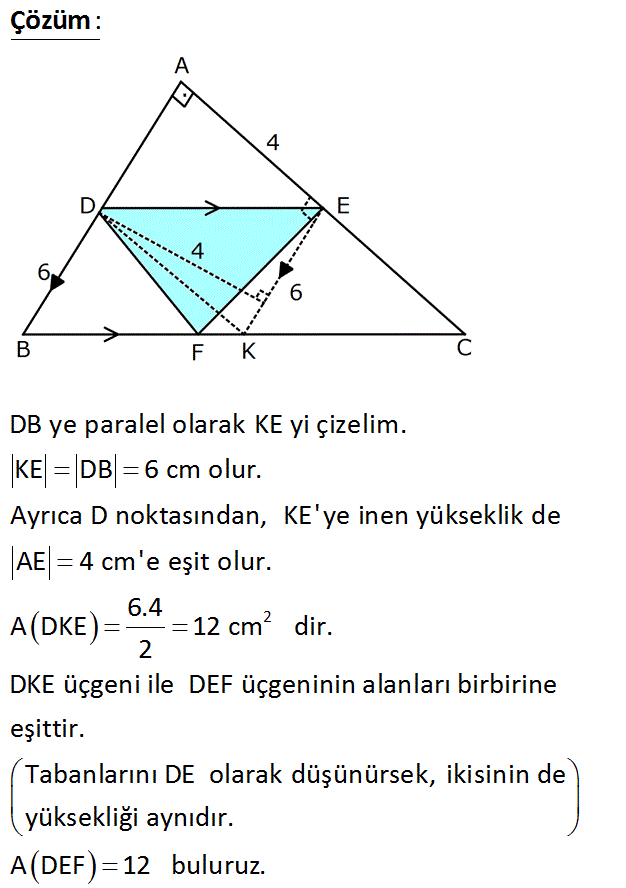
Taralı alan ? : Çözüm www.matematikkolay.net 2 DB ye paralel olarak KE yi çizelim. KE DB 6 cm olur. Ayrıca D noktasından, KE’ ye inen yükseklik de AE 4 cm’e eşit olur. 06.Nis A DKE 12 cm dir. 2 DKE üçgeni ile DEF üçgeninin alanları birbirine eşittir. Tab anlarını DE olarak düşünürsek, ikisinin de yüksekliği aynıdır. A DEF 12 buluruz. 56
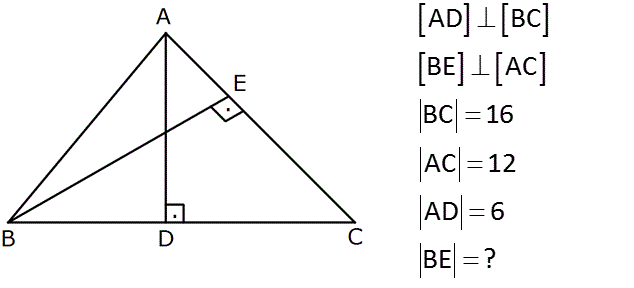
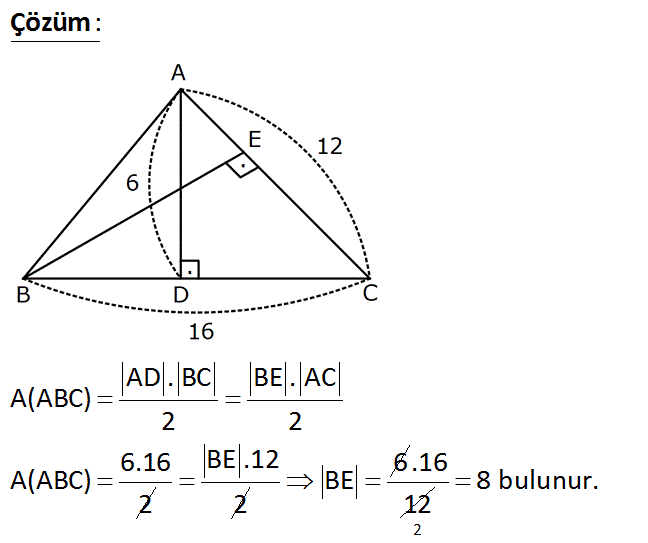
AD BC BE AC BC 16 AC 12 AD 6 BE ? Çözüm: www.matematikkolay.net AD . BC BE . AC A(ABC) 2 2 Haz.16 A(ABC) 2 BE .12 2 6 BE .16 12 2 8 bulunur. 9
www.matematikkolay.net A(AEF) A(FDC) AE 5 cm BE 10 cm BD 7 cm Buna göre, DC x kaç cm dir? 3 5 7 A) B) 2 C) D) 3 E) 2 2 2 : Çözüm www.matematikkolay.net Eşit alanlara S diyelim. A(AEF) A(FDC) S ABD üçgeninin alanı A S dir BEC üçgeninin alanı da A S dir. O halde; A(ABD) A(BEC) 1 2 AB BD sin 1 2 BE BC sin 15 3 7 10 2 (7 x) 21 14 2x 7 2x 7 x buluruz. 2 30
a b c a b c a, b ve c bir üçgenin kenar uzunluklarını; h , h ve h de kenarlara ait yükseklikleri göstermektedir. a b 9 1 1 1 h h h olduğuna göre, c kaçtır? A) 2 B) 3 C) 4 D) 6 E) 9 a a b c Bir üçgenin kenarı ile o kenara ait yükseklik çarpılıp, yarıya bölünürse o üçgenin alanı bulunur. a.h Örneğin; A dır. 2 a.h 2A diyebiliriz. Aynı şekilde; b.h 2A ve c.h 2A dır. : Buna göre Çözüm a b c a b c a b c ; 1 1 1 a b c h h h a.h b.h c.h a b c 2A 2A 2A a b 2A c 2A a b c 9 c buluruz. 46

