Soru Sor sayfası kullanılarak Üçgende Alan konusu altında Benzerlik ve Üçgende Alan, S-3S-5S ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
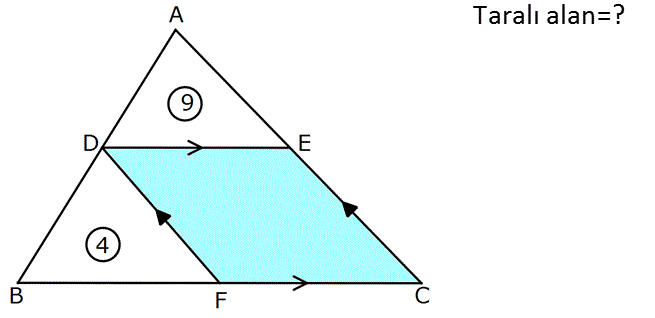
2.SORU
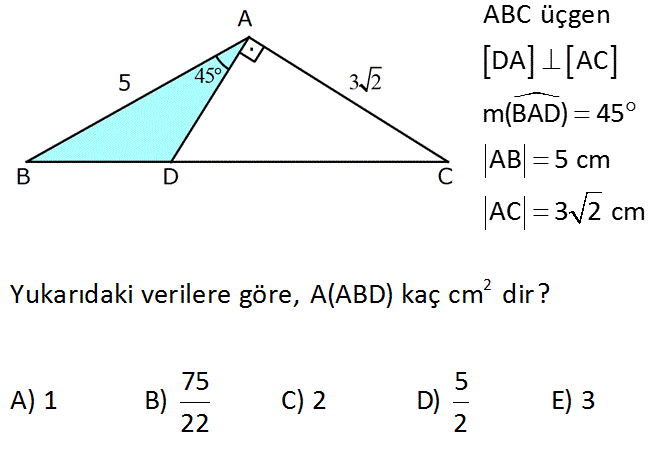
3.SORU
4.SORU
5.SORU

6.SORU
7.SORU
8.SORU
Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
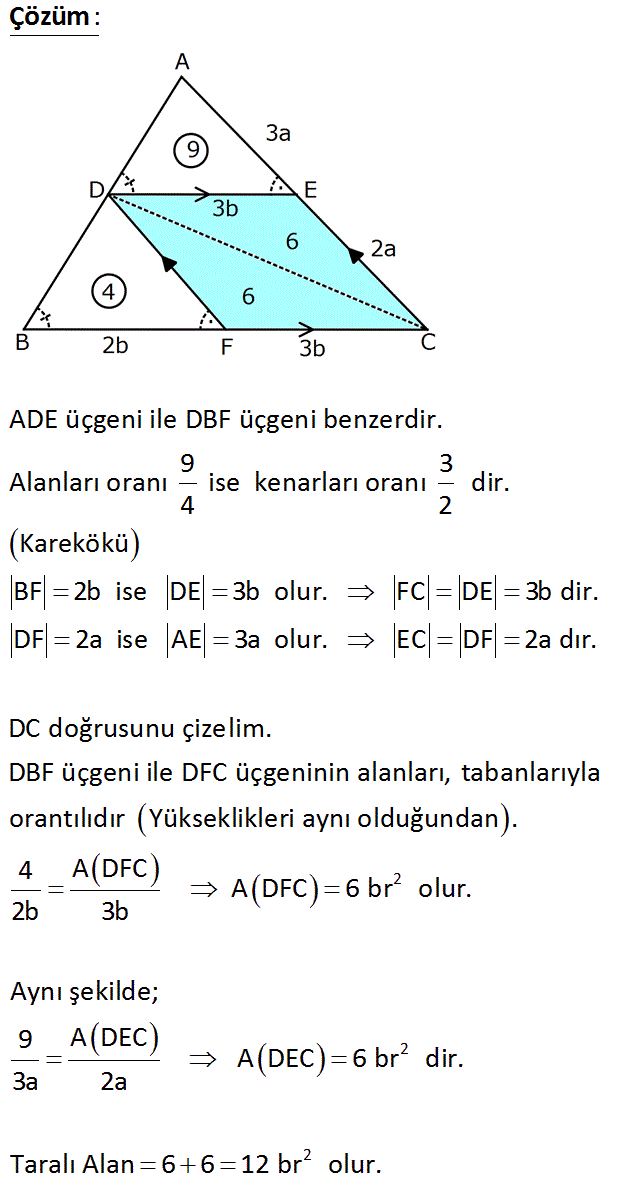
www.matematikkolay.net Taralı alan=? : Çözüm www.matematikkolay.netADE üçgeni ile DBF üçgeni benzerdir. 9 3 Alanları oranı ise kenarları oranı dir. 4 2 Karekökü BF 2b ise DE 3b olur. FC DE 3b dir. DF 2a ise AE 3a olur. EC DF 2a dır. DC doğrusunu çizelim. DBF üç 2 2 2 geni ile DFC üçgeninin alanları, tabanlarıyla orantılıdır Yükseklikleri aynı olduğundan . 4 A DFC A DFC 6 br olur. 2b 3b Aynı şekilde; 9 A DEC A DEC 6 br dir. 3a 2a Taralı Alan 6 6 12 br olur. 49
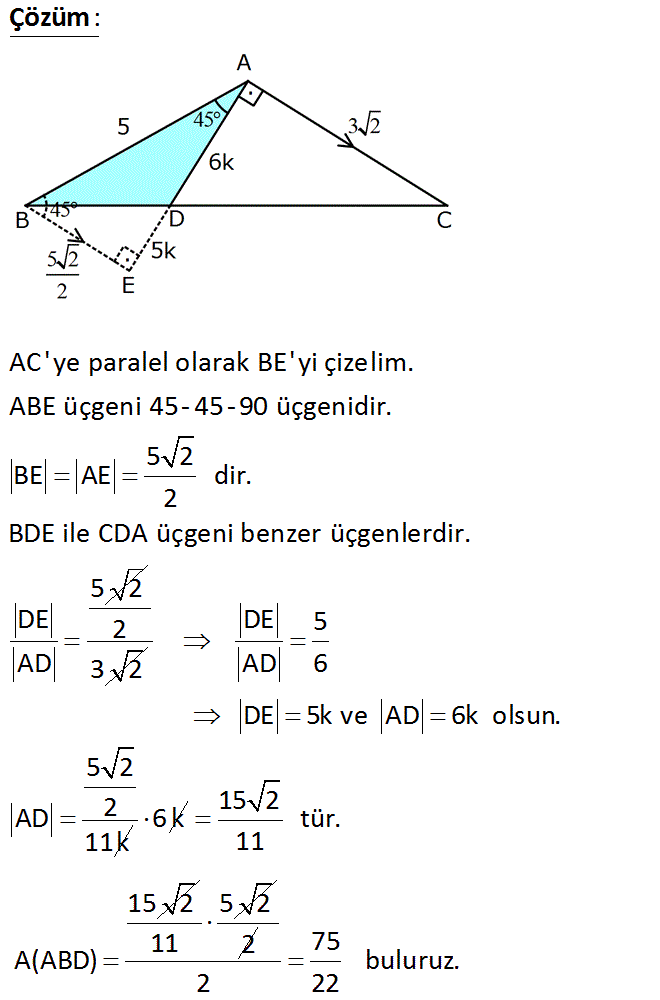
ABC üçgen DA AC m(BAD) 45 AB 5 cm AC 3 2 cm 2 Yukarıdaki verilere göre, A(ABD) kaç cm dir? 75 5 A) 1 B) C) 2 D) E) 3 22 2 : Çözüm www.matematikkolay.net AC’ye paralel olarak BE’yi çizelim. ABE üçgeni 45- 45-90 üçgenidir. 5 2 BE AE dir. 2 BDE ile CDA üçgeni benzer üçgenlerdir. 5 2 DE AD 2 3 2 DE 5 AD 6 DE 5k ve AD 6k olsun. 5 2 AD 2 11k 6 k 15 2 tür. 11 15 2 A(ABD) 5 2 11 2 75 buluruz. 2 22 27
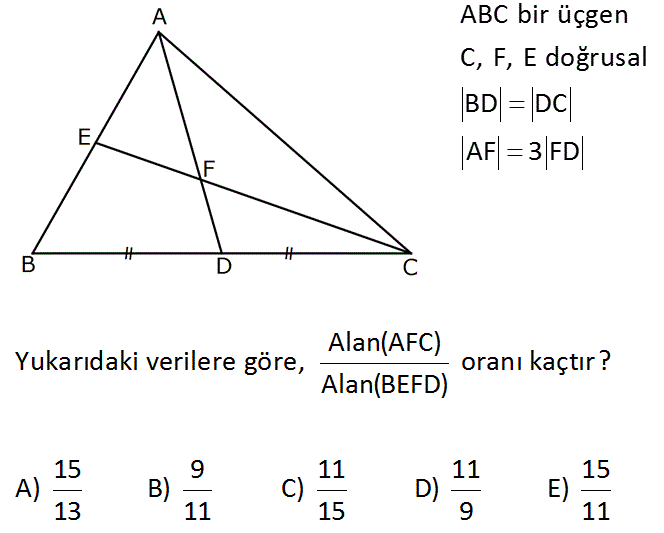
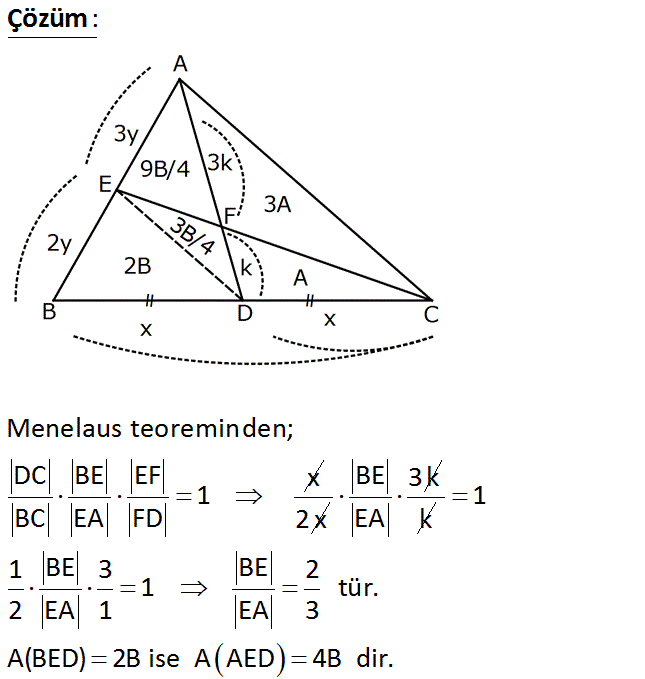
ABC bir üçgen C, F, E doğrusal BD DC AF 3 FD Alan(AFC) Yukarıdaki verilere göre, oranı kaçtır? Alan(BEFD) 15 9 11 11 15 A) B) C) D) E) 13 11 15 9 11 : Çözüm Menelaus teoreminden; DC BE EF x 1 BC EA FD 2 x BE 3k EA k1 1 BE 3 BE 2 1 tür. 2 EA 1 EA 3 A(BED) 2B ise A AED 4B dir. 44
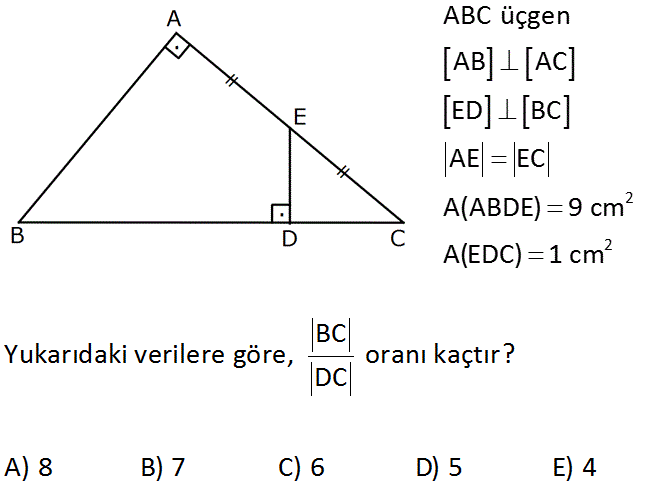
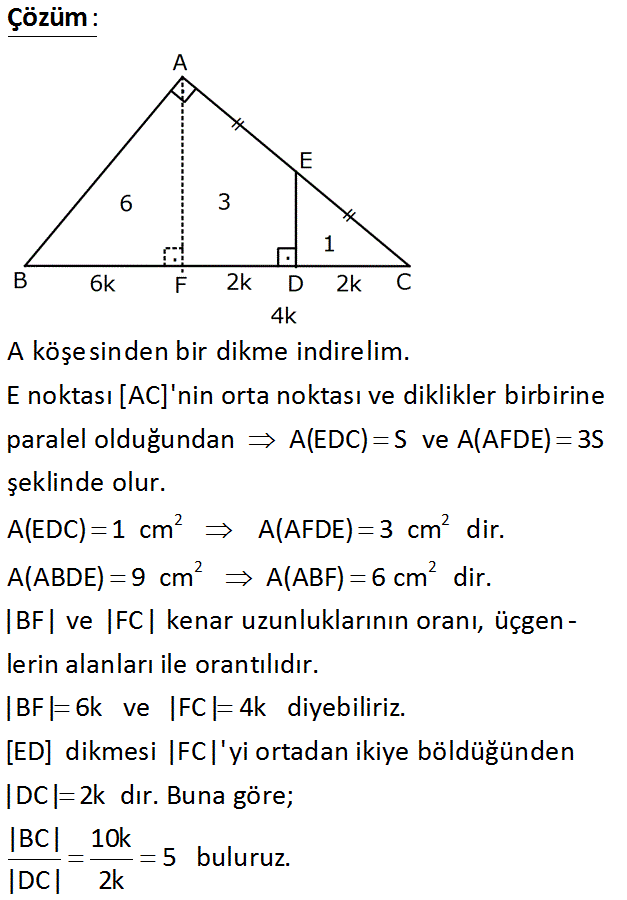
2 2 ABC üçgen AB AC ED BC AE EC A(ABDE) 9 cm A(EDC) 1 cm www.matematikkolay.net BC Yukarıdaki verilere göre, oranı kaçtır? DC A) 8 B) 7 C) 6 D) 5 E) 4 Çözüm: 2 2 2 A köşesinden bir dikme indirelim. E noktası [AC]’nin orta noktası ve diklikler birbirine paralel olduğundan A(EDC) S ve A(AFDE) 3S şeklinde olur. A(EDC) 1 cm A(AFDE) 3 cm dir. A(ABDE) 9 cm 2 A(ABF) 6 cm dir. |BF| ve |FC| kenar uzunluklarının oranı, üçgenlerin alanları ile orantılıdır. |BF| 6k ve |FC| 4k diyebiliriz. [ED] dikmesi |FC|’yi ortadan ikiye böldüğünden |DC| 2k dır. Buna göre; |BC| 10k 5 buluruz. |DC| 2k 14
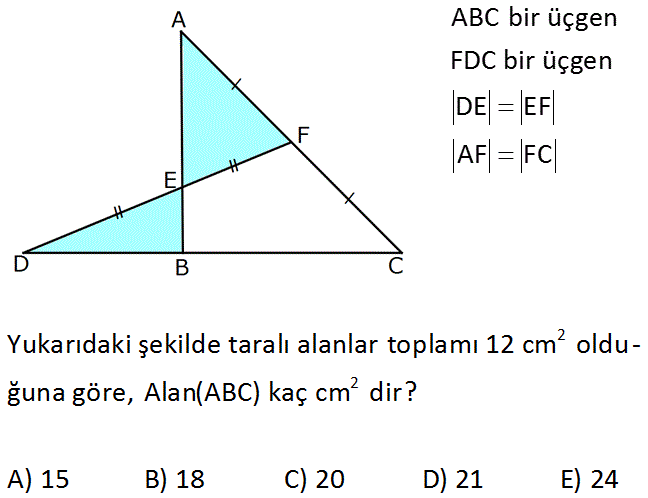
ABC bir üçgen FDC bir üçgen DE EF AF FC 2 2 Yukarıdaki şekilde taralı alanlar toplamı 12 cm oldu – ğuna göre, Alan(ABC) kaç cm dir? A) 15 B) 18 C) 20 D) 21 E) 24 www.matematikkolay.net : Çözüm BC Menelaus yöntemi ile oranını bulalım. BD AF BC DE 1 AC BD EF 1 BC 1 1 BC 2k ve BD k diyebiliriz. 2 BD 1 A BED A olsun. A BEC 2A olur. ED EF olduğundan A EFC A DEC A 2A 3A dır. AF FC olduğundan A AFE A FCE 3A dır. Taralı alanlar to plamı: A 3A 12 4A 12 A 3 tür. A ABC 2A 3A 3A 8A 8.3 24 buluruz. www.matematikkolay.net 50
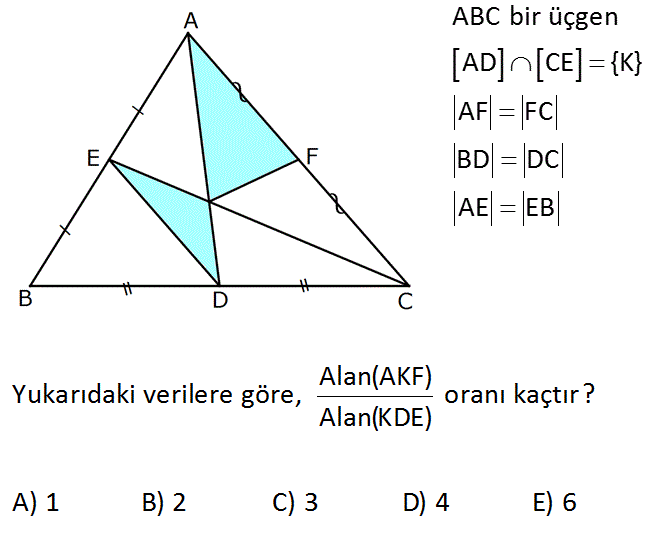
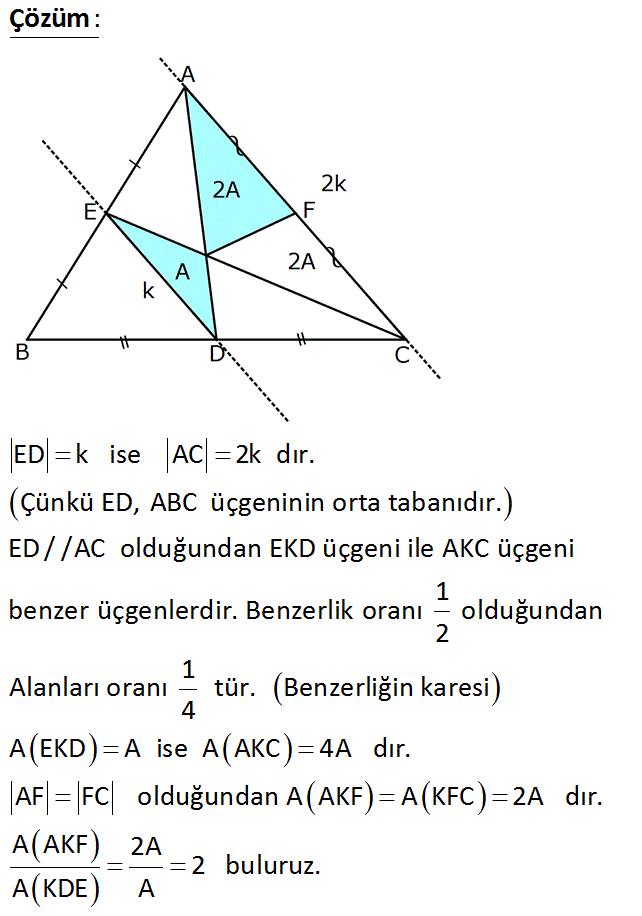
ABC bir üçgen AD CE {K} AF FC BD DC AE EB Alan(AKF) Yukarıdaki verilere göre, oranı kaçtır? Alan(KDE) A) 1 B) 2 C) 3 D) 4 E) 6 : Çözüm www.matematikkolay.net ED k ise AC 2k dır. Çünkü ED, ABC üçgeninin orta tabanıdır. ED / /AC olduğundan EKD üçgeni ile AKC üçgeni 1 benzer üçgenlerdir. Benzerlik oranı olduğundan 2 1 Alanları oranı tür. Benzerliğin karesi 4 A EKD A ise A AKC 4A dır. AF FC olduğundan A AKF A KFC 2A dır. A AKF 2A 2 buluruz. A KDE A 51
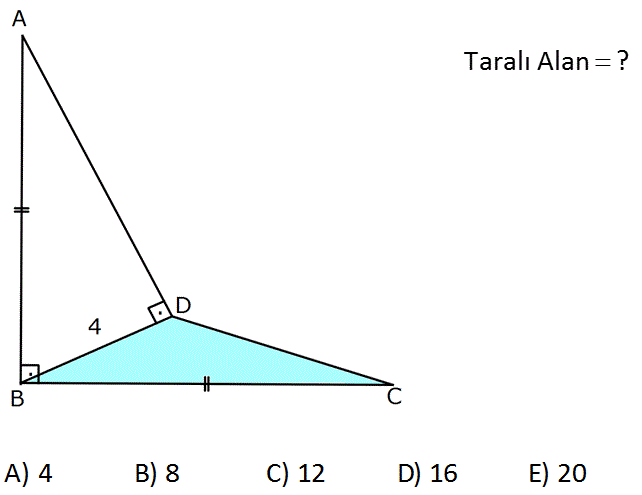
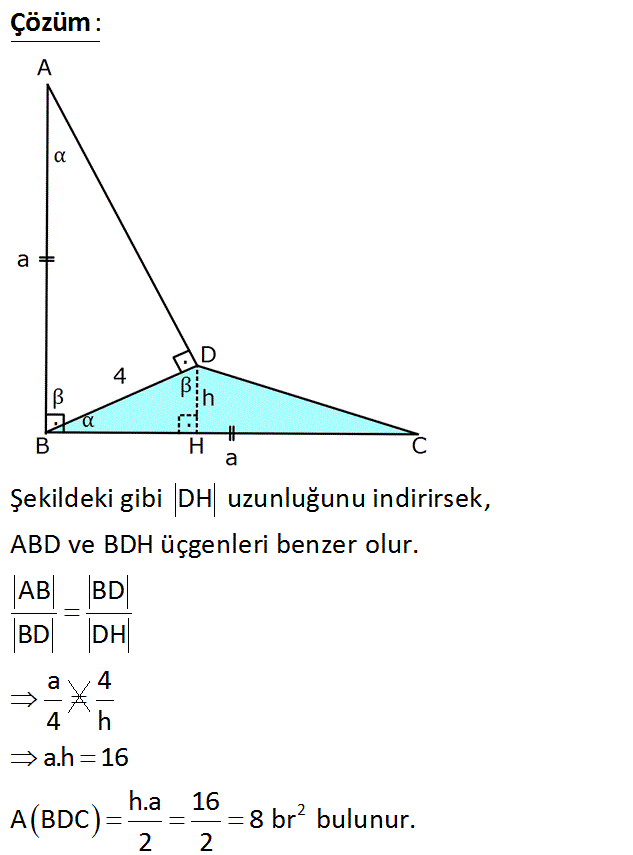
www.matematikkolay.net Taralı Alan ? A) 4 B) 8 C) 12 D) 16 E) 20 : Çözüm Şekildeki gibi DH uzunluğunu indirirsek, ABD ve BDH üçgenleri benzer olur. AB BD BD DH a 4 2 4 h a.h 16 h.a 16 A BDC 8 br bulunur. 2 2 www.matematikkolay.net 17
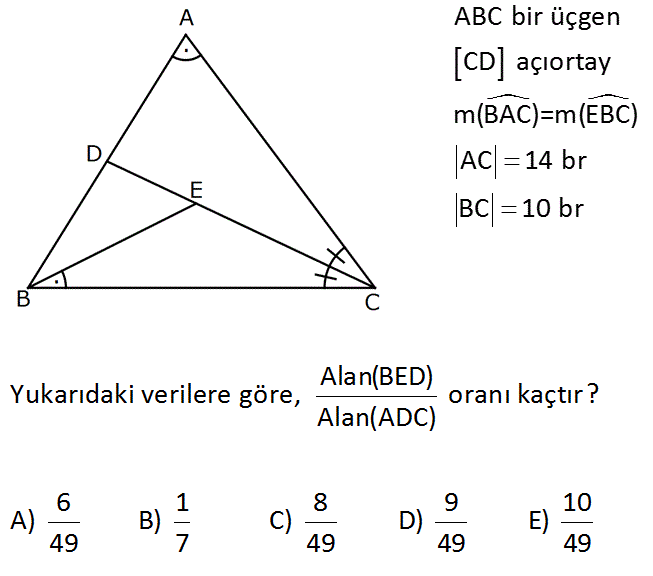
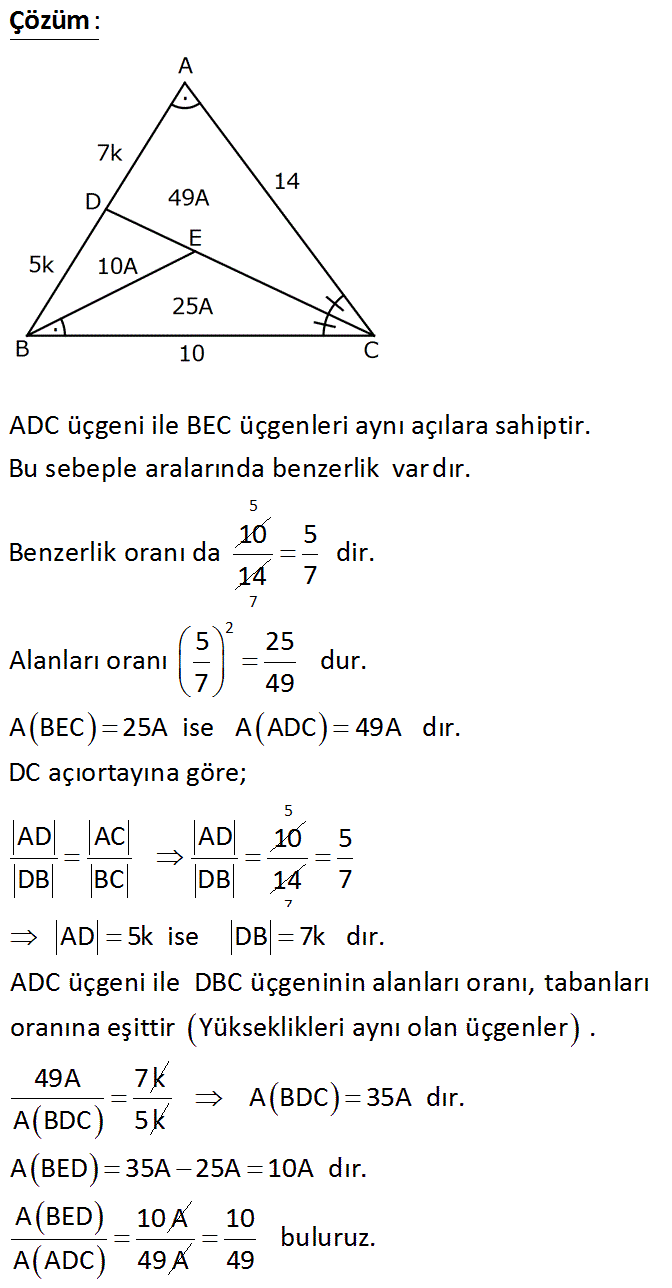
ABC bir üçgen CD açıortay m(BAC)=m(EBC) AC 14 br BC 10 br Alan(BED) Yukarıdaki verilere göre, oranı kaçtır? Alan(ADC) 6 1 8 9 10 A) B) C) D) E) 49 7 49 49 49 www.matematikkolay.net : Çözüm ADC üçgeni ile BEC üçgenleri aynı açılara sahiptir. Bu sebeple aralarında benzerlik var dır. 10 Benzerlik oranı da 5 14 7 2 5 dir. 7 5 25 Alanları oranı dur. 7 49 A BEC 25A ise A ADC 49A dır. DC açıortayına göre; AD AC AD 10 DB BC DB 5 14 7 5 7 AD 5k ise DB 7k dır. ADC üçgeni ile DBC üçgeninin alanları oranı, tabanları oranına eşittir Yükseklikleri aynı olan üçgenler . 49A 7k A BDC 5k A BDC 35A dır. A BED 35A 25A 10A dır. A BED 10 A A ADC 49 A 10 buluruz. 49 52

