Soru Sor sayfası kullanılarak Üçgende Alan konusu altında Açıortay ve Alan, İç Teğet Çemberi ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
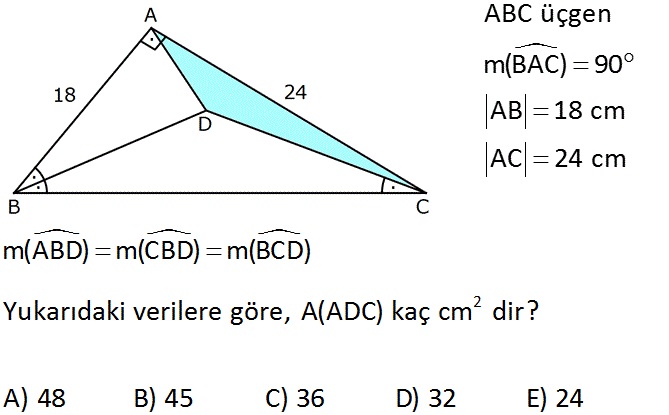

2.SORU
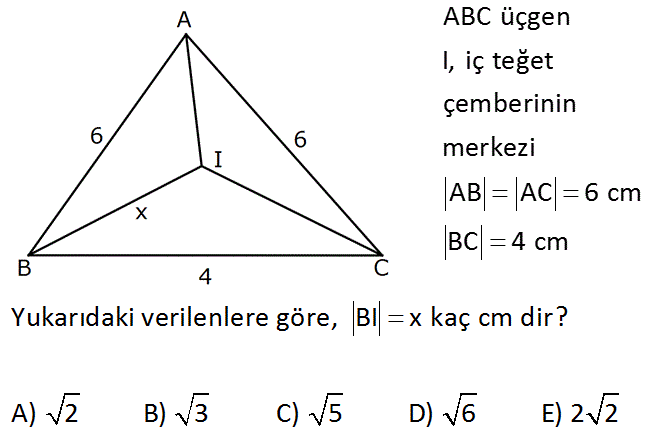

3.SORU
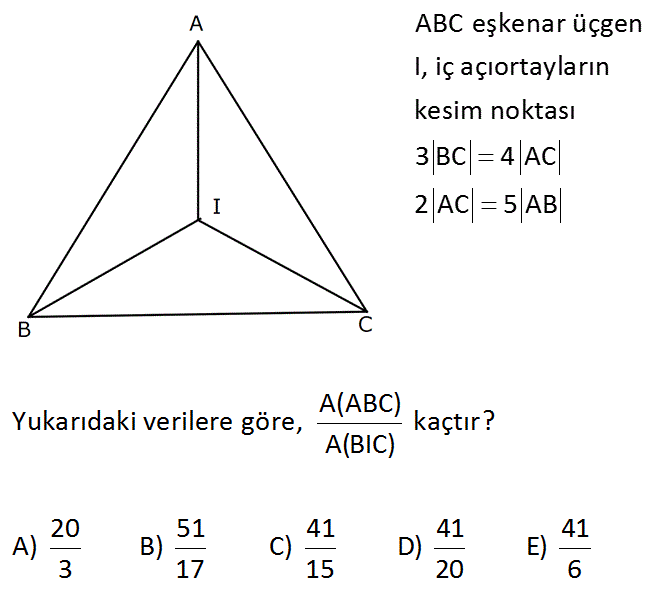
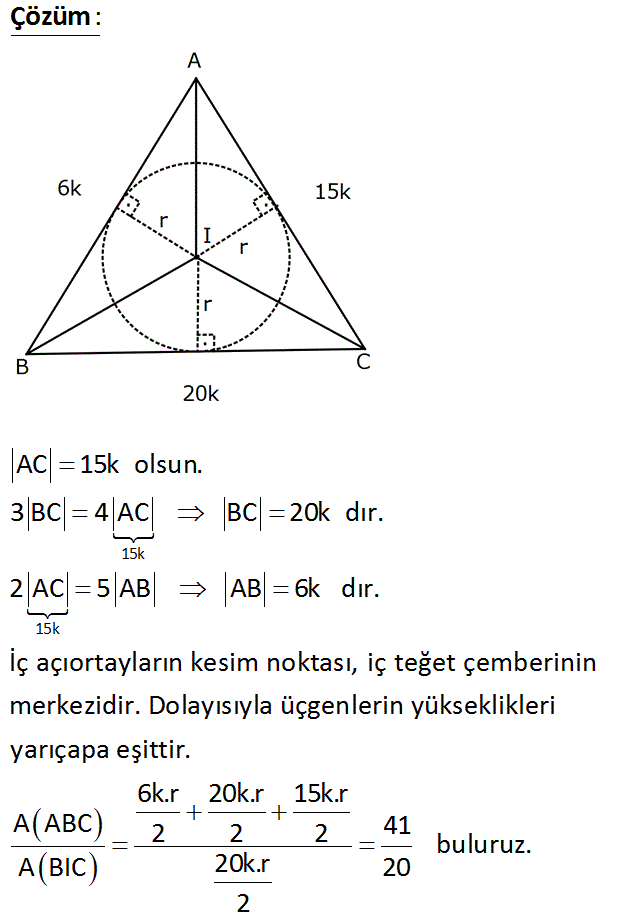
4.SORU

5.SORU

Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
ABC üçgen m(BAC) 90 AB 18 cm AC 24 cm 2 m(ABD) m(CBD) m(BCD) Yukarıdaki verilere göre, A(ADC) kaç cm dir? A) 48 B) 45 C) 36 D) 32 E) 24 www.matematikkolay.net : Çözüm ABC üçgeni 18,24,30 üçgenidir. (3k – 4k – 5k) BC kenarına D noktasından indireceğimiz bir dikme kenarı iki eşit parçaya ayırır. 15 Açıortaydan, kollarına inilen dikmeler birbirine eşit olduğu gibi, kollard 2 aki kısımlar da birbirine eşittir. Dolayısıyla |AB| uzunluğu 15 ve 3 olarak ikiye ayrılır. 3 uzunluğu da ADC üçgeninin yüksekliğine eşittir. 24.Mar A(ADC) 36 cm buluruz. 2 8
ABC üçgen I, iç teğet çemberinin merkezi AB AC 6 cm BC 4 cm Yukarıdaki verilenlere göre, BI x kaç cm dir? A) 2 B) 3 C) 5 D) 6 E) 2 2 : Çözüm www.matematikkolay.net 2 2 2 2 A’dan F’ye yükseklik indirelim. ABC ikizkenar üçgen olduğu için BC, 2 eş parçaya ayrılır. 2 ve 2 AFC’de pisagor uygulayarak üçgeninin yüksekliğini bulalım. AF 2 6 AF 32 AF 4 2 dir. 04.Nis A(ABC) 2 2 2 2 2 8 2 dir. 2 İç teğet çemberinin yarıçapı r, Çevre u ise A(ABC) u.r ile bulunur. 2 6 6 4 u 8 2 O halde; 8.r 8 2 r 2 dir. BIF üçgeninde pisagordan; x 2 2 x 4 2 x 6 buluruz. 39
ABC eşkenar üçgen I, iç açıortayların kesim noktası 3 BC 4 AC 2 AC 5 AB www.matematikkolay.net A(ABC) Yukarıdaki verilere göre, kaçtır? A(BIC) 20 51 41 41 41 A) B) C) D) E) 3 17 15 20 6 : Çözüm 15k 15k AC 15k olsun. 3 BC 4 AC BC 20k dır. 2 AC 5 AB AB 6k dır. İç açıortayların kesim noktası, iç teğet çemberinin merkezidir. Dolayısıyla üçgenlerin yükseklikleri yarıçapa eşittir. 6k.r 20 A ABC 2 A BIC k.r 15k.r 2 2 41 buluruz. 20k.r 20 2 64
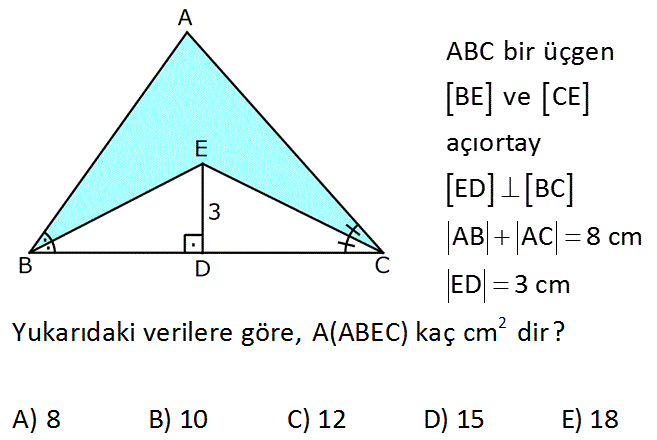
www.matematikkolay.net ABC bir üçgen BE ve CE açıortay ED BC AB AC 8 cm ED 3 cm 2 Yukarıdaki verilere göre, A(ABEC) kaç cm dir? A) 8 B) 10 C) 12 D) 15 E) 18 : Çözüm Açıortaydan kollara inilen dikmeler birbirine eşittir. Dolayısıyla, taralı alanı iki üçgen olarak iki parçaya ayırırsak; bu üçgenlere ait yükseklikler 3’er cm olur. A(ABEC) A(AEB) A(AEC) 2 AB .3 AC .3 2 2 3 AB AC 2 3 8 2 12 cm buluruz. www.matematikkolay.net 38
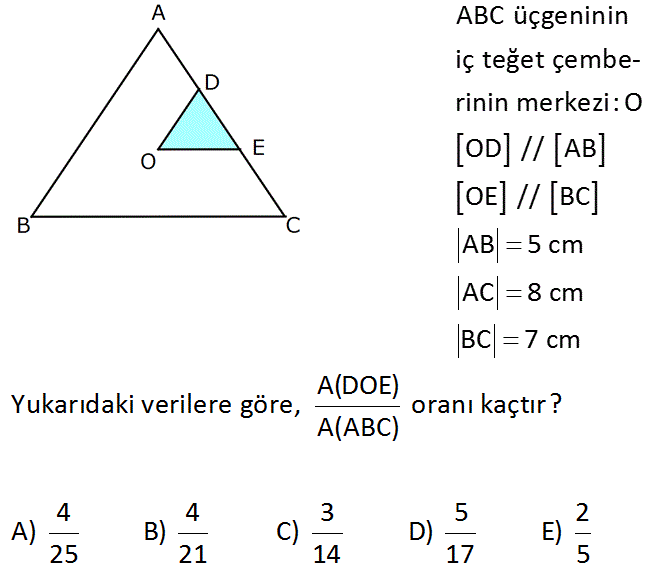
ABC üçgeninin iç teğet çemberinin merkezi:O OD // AB OE // BC AB 5 cm AC 8 cm BC 7 cm A(DOE) Yukarıdaki verilere göre, oranı kaçtır? A(ABC) 4 4 3 5 2 A) B) C) D) E) 25 21 14 17 5 : Çözüm www.matematikkolay.net m(BAO) m(DAO) (Açıortay) ve m(BAO) m(DOA) iç ters açılar ([OD] / /[AB]) AD a ise DO a dır. m(BCO) m(ECO) (Açıortay) ve m(BCO) m(COE) iç ters açılar ([OE] / /[AC]) EC b ise OE b dir. DE 8 (a b) dir. Buna göre; Çevre(DOE) a b 8 (a b) 8 dir. Çevre(ABC) 5 8 7 20 dir. Paralel doğrular nedeniyle ABC üçgeninin açıları ile DOE üçgeninin açıları aynıdır. Bu sebeple benzer – lik uygulayabiliriz. Alan ları oranı, benzerliğin karesi – dir. A(DOE) 8 A(ABC) 2 20 2 2 5 2 4 buluruz. 5 25 20

