Soru Sor sayfası kullanılarak Öklit Bağıntıları konusu altında Öklit kullanılan karışık sorular, Öklit güzel sorular ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU

2.SORU

3.SORU


4.SORU

5.SORU
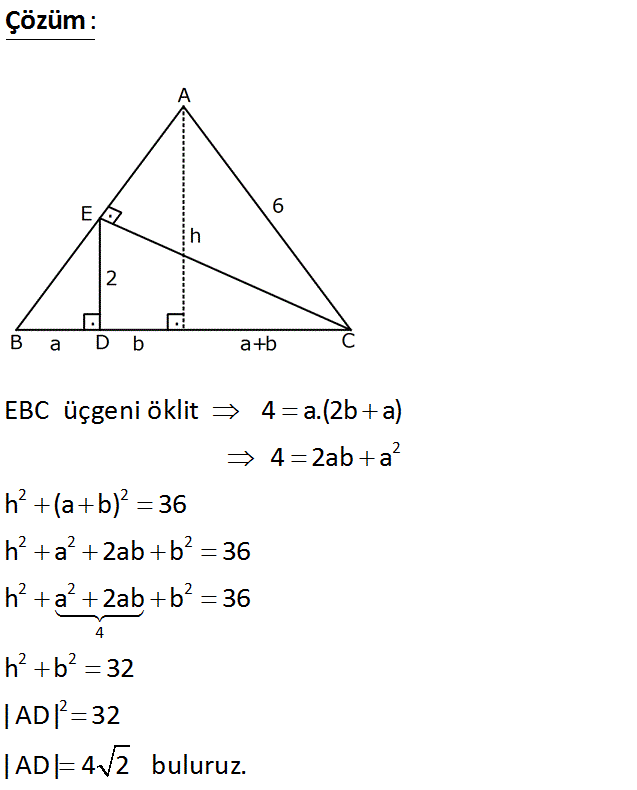
6.SORU

7.SORU

Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
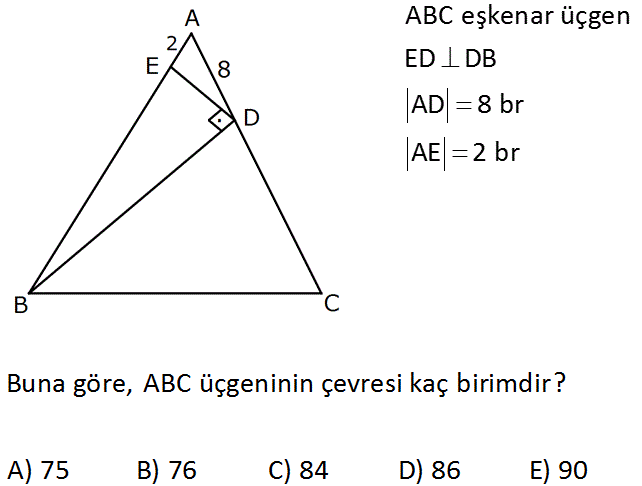
ABC eşkenar üçgen ED DB AD 8 br AE 2 br Buna göre, ABC üçgeninin çevresi kaç birimdir? A) 75 B) 76 C) 84 D) 86 E) 90 : Çözüm D noktasından AB kenarına bir dik indirirsek; Burada bir 30 -60 -90 üçgeni oluşur. Bir kenarı 8 olduğundan, diğer kenarları 4 ve 4 3 şeklinde olur. |AE| 2 olduğundan, kenarın kalan kısmı da 2 birim olur. Daha 2 sonra EDB üçgenininde öklit teoremi uygulayarak, |BF|’ yi bulabiliriz. |BF|.2 (4 3) |BF|.2 48 |BF| 24 birimdir. Buna göre; eşkenar üçgenin bir kenarı 24 4 28 Çevresini de 28.3 84 birim buluruz. 6
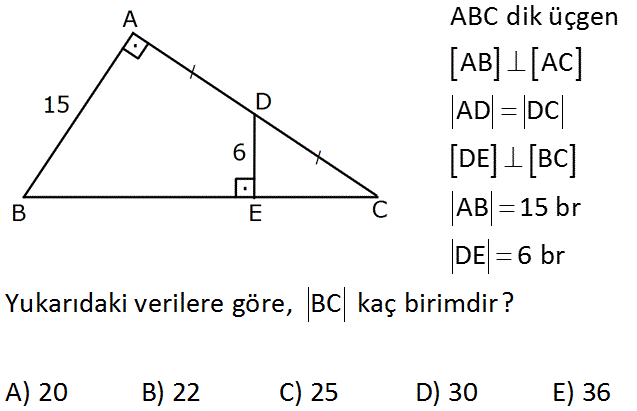
ABC dik üçgen AB AC AD DC DE BC AB 15 br DE 6 br Yukarıdaki verilere göre, BC kaç birim A) 20 B) 22 C) 25 D) 30 E) 36 dir? Çözüm: 2 AH uzunluğunu çizersek AHC üçgeninde benzerlik oranından AH 12 br olur. BH 9 br olur.(9 -12-15) Şimdi öklid uygulayalım. BC x br olsun. 225 15 9.x x 25 br bulunur. 9 10
AB AD m(ACB) 45 BD 5 cm DC 1 cm Yukarıdaki verilere göre, AC x aşağıdakilerden hangi A) 2 B) 2 2 C) sine eşit o 3 D) 3 2 E) 5 labil ir? Çözüm: www.matematikkolay.net 2 2 2 2 2 2 A’dan bir dikme indirdiğimizde 45 45 90 üçgeni oluşur. Bu dikmenin uzunluğuna a cm dersek, Taban a 1 ve 6 a olarak ayrılır. Öklit teoremini kullanalım. a (6 a)(a 1) a 6a 6 a a a 7a 6 a 2a 7a 6 0 49 4. 2.6 49 48 1 dir. b 7 1 8 6 x veya tür. 2a 4 4 4 8 2 ‘yi kullanalım. 4 45- 45-90 üçgenine göre x a 2 2 2 buluruz. 12
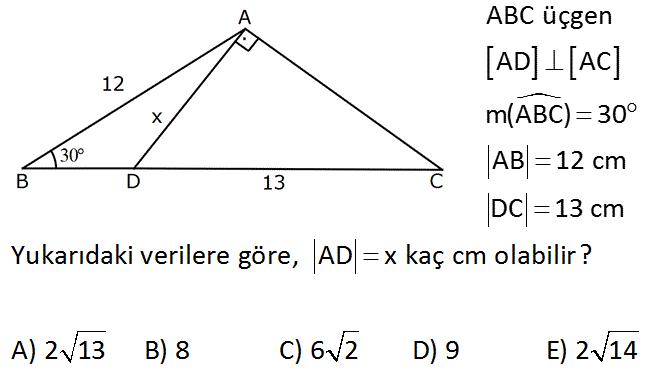
www.matematikkolay.net ABC üçgen AD AC m(ABC) 30 AB 12 cm DC 13 cm Yukarıdaki verilere göre, AD x kaç cm A) 2 13 B) 8 C) 6 2 D) o 9 labi E) 2 lir? 14 Çözüm: www.matematikkolay.net 2 2 2 a.a 9. 4 AH yüksekliğini indirirsek 30 – 60 – 90 üçgeninin 12 özelliğinden 30 nin karşısındaki AH 6 cm olur. 2 ADC dik üçgeninde öklit uygulayalım. DH a, HC 13 a olsun. 6 a 13 a 36 13a a a 13a 36 0 a 9 a 4 0 a 9 2 2 2 2 2 2 2 2 veya a 4 tür. a 9 x 9 6 x 117 x 3 13 olur. a 4 x 4 6 x 52 x 2 13 bulunur. Şıklarda bu değer var. 16
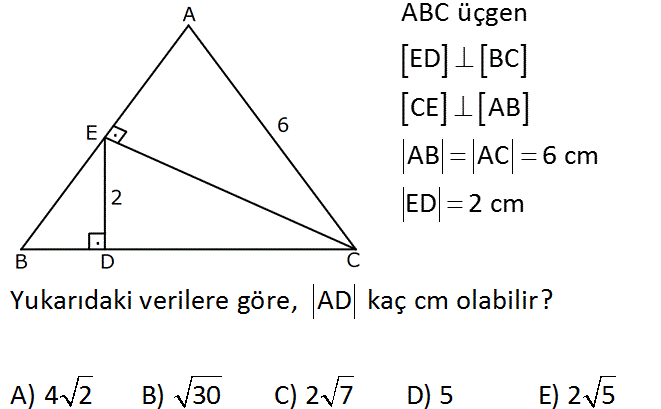
ABC üçgen ED BC CE AB AB AC 6 cm ED 2 cm Yukarıdaki verilere göre, AD kaç cm o A) 4 2 B) 30 C) 2 7 D) 5 E) labil 2 5 ir? Çözüm: www.matematikkolay.net 2 2 2 2 2 2 2 2 2 4 2 2 2 EBC üçgeni öklit 4 a.(2b a) 4 2ab a h (a b) 36 h a 2ab b 36 h a 2ab b 36 h b 32 |AD| 32 |AD| 4 2 buluruz. 17
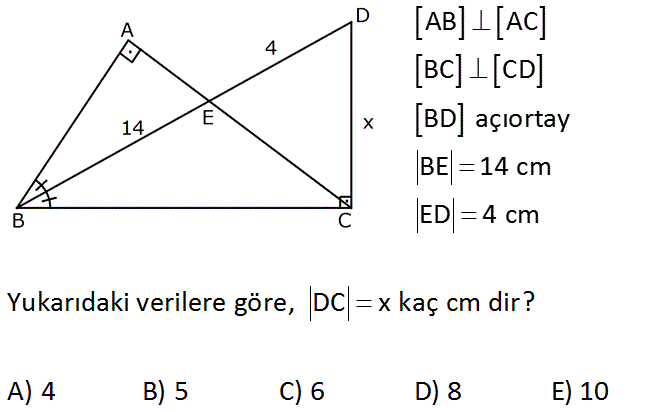
AB AC BC CD BD açıortay BE 14 cm ED 4 cm Yukarıdaki verilere göre, DC x kaç c A) 4 B) 5 C) 6 D) 8 E) 10 m di r? www.matematikkolay.net : Çözüm Açıortayın açılarına a diyelim. m(AEB) b olsun. m(CDB) b olur. (a b 90 olduğundan) Ayrıca m(AEB) m(DEC) b dir. O halde; ECD üçgeni ikizkenar bir üçgendir. C noktasından indireceğimiz yükseklik ED yi i 2 2 ki eş parçaya ayırır. m(BCD) açısı da dik açı olduğundan, öklit uygulayabiliriz. (Yan dik kenarı bulma) x 2.18 x 36 x 6 buluruz. 18
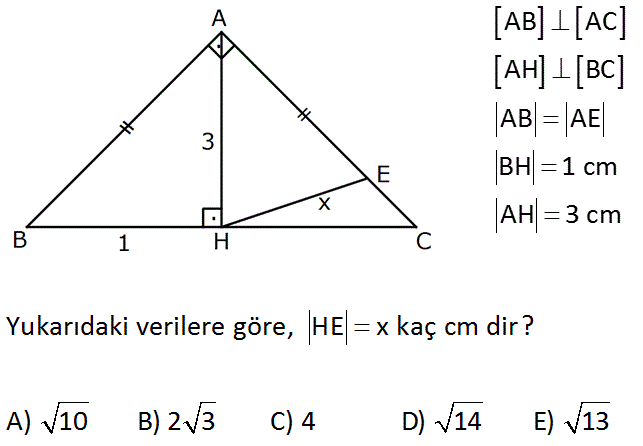
AB AC AH BC AB AE BH 1 cm AH 3 cm Yukarıdaki verilere göre, HE x kaç cm dir? A) 10 B) 2 3 C) 4 D) 14 E) 13 www.matematikkolay.net : Çözüm 2 2 2 3 2 2 ABC üçgeninde öklit teoreminden; |AH| |BH|.|HC| 3 1.|HC| |HC| 9 dur. ABH üçgeninde pisagor teoreminden; |AB| 1 3 10 dur. AHC üçgeninde pisagor teoreminden; |AC| 3 9 9 81 90 3 10 dur. |AC| |A 2 2 B| 10 dur. |EC| 3 10 10 2 10 E köşesinden D’ ye bir dikme indirirsek; iki benzer üçgen elde ederiz. AHC EDC Bu benzerlikten; |HD| 3 ve |ED| 2 buluruz. EDH üçgeninde pisagordan; x 2 3 4 9 13 bu luruz. 3

