Soru Sor sayfası kullanılarak Üçgende Açı Kenar Bağıntıları konusu altında Büyük açının karşısı, Küçük açının karşısı ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU


2.SORU

3.SORU
4.SORU

5.SORU

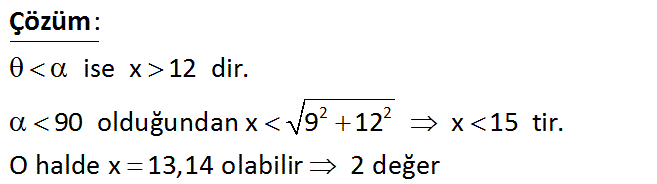
6.SORU

7.SORU
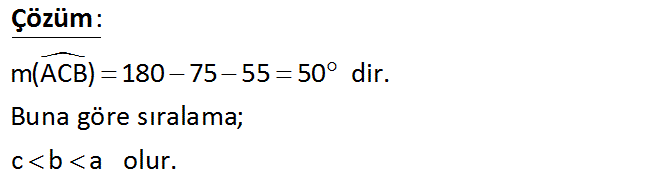
8.SORU


Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
ABC üçgen AB c AC b BC a m(BAC) 71 m(ABC) 53 Yukarıdaki verilere göre, a, b, c arasındaki ilişki aşağıdakilerden hangisidir? A) a b c B) a c b C) b c a D) c b a E) b a c : Çözüm Büyük açının karşısında büyük kenar olur. Buna göre; a c b bulunur. 4
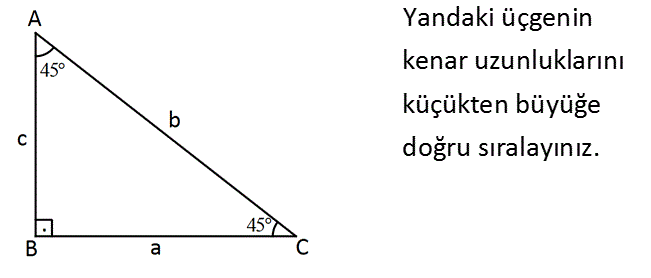
www.matematikkolay.net Yandaki üçgenin kenar uzunluklarını küçükten büyüğe doğru sıralayınız. Eşit açının karşısında eşit kenar olur. Bu sebeple a c dir. Büyük açının karşısında da büyük kenar olur. Buna göre sıralama; a c b r. : di Çözüm 30
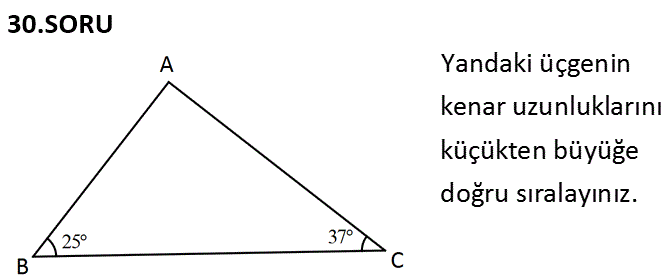
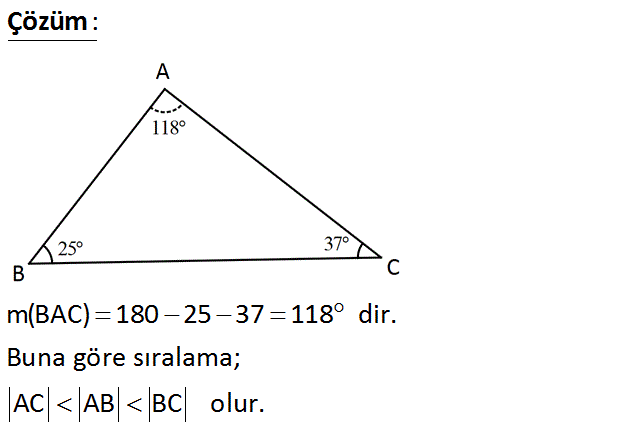
Yandaki üçgenin kenar uzunluklarını küçükten büyüğe doğru sıralayınız. Çözüm: m(BAC) 180 25 37 118 dir. Buna göre sıralama; AC AB BC olur. www.matematikkolay.net 31
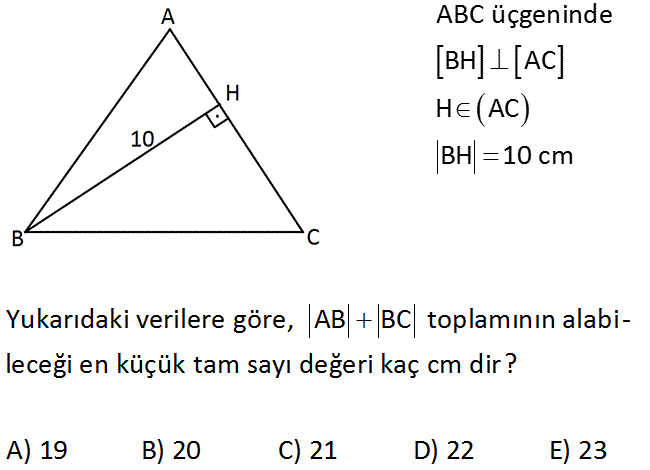
www.matematikkolay.net ABC üçgeninde BH AC H AC BH 10 cm Yukarıdaki verilere göre, AB BC toplamının alabi – leceği en küçük tam sayı değeri kaç cm dir? A) 19 B) 20 C) 21 D) 22 E) 23 ABH üçgeninde |AB| kenarı hipotenüs olduğundan; |AB| 10 olmalıdır. Aynı şekilde; BHC üçgeninde |BC| kenarı hipotenüs olduğundan; |BC| 10 olmalıdır. İkisini toplarsak; |AB| |BC| 10 10 |AB| : |BC| 20 Çözüm O halde; |AB| |BC| en küçük 21 olabilir. 23
ABC üçgen m(BAC) m(ABC) AB 9 cm AC 12 cm www.matematikkolay.net Yukarıdaki şekilde, 90 olduğuna göre, x in alabileceği kaç farklı tam sayı değeri vardır? A) 1 B) 2 C) 3 D) 4 E) 5 2 2 ise x 12 dir. 90 olduğundan x 9 12 x 15 tir. O halde x 13,14 olabilir 2 de : ğer Çözüm 24
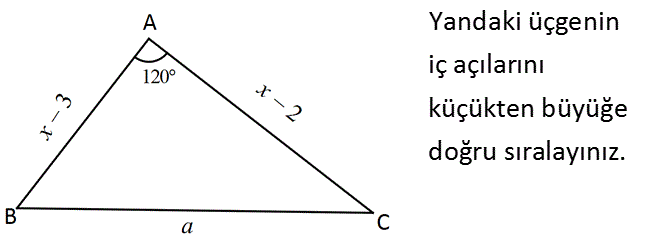
Yandaki üçgenin iç açılarını küçükten büyüğe doğru sıralayınız. A açısı 120 ise diğer iki iç açının toplamı 60 dir. Dolayısıyla en büyük açı A açısıdır. c b olduğundan Cˆ Bˆ dir. O halde sıralama; Cˆ Bˆ Aˆ olur. : Çözüm 32
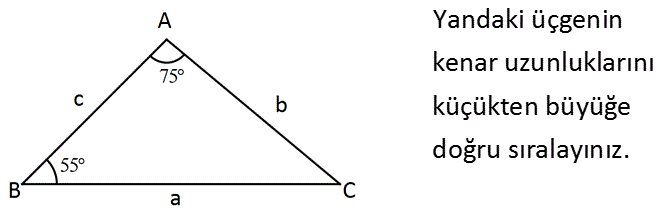
Yandaki üçgenin kenar uzunluklarını küçükten büyüğe doğru sıralayınız. m(ACB) 180 75 55 50 dir. Buna göre sıralama; c b a o : lur. Çözüm 33
ABC bir üçgen AB 3 cm AC 5 cm BC x Yukarıdaki verilere göre, m(ABC) m(ACB) 60 olduğuna göre, x in en büyük tam sayı değeri kaç cm dir? A) 3 B) 4 C) 5 D) 6 E) 7 : Çözüm 2 2 2 2 m(ABC) m(ACB) 60 m(BAC) 120 m(BAC) 120 olsa idi; x 3 5 2.3.5.cos120 (kosinüs teoremi) x 9 25 2 1 .3.5. 2 2 2 x 34 15 x 49 x 7 olurdu. açı 120 den küçük olduğu için x 7 olmalı. x’in en büyük değeri 6 bulunur. 10

