Soru Sor sayfası kullanılarak Üçgende Benzerlik konusu altında Eşkenar üçgen çizerek benzerlik kurma ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
2.SORU

3.SORU

4.SORU
5.SORU
6.SORU
Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
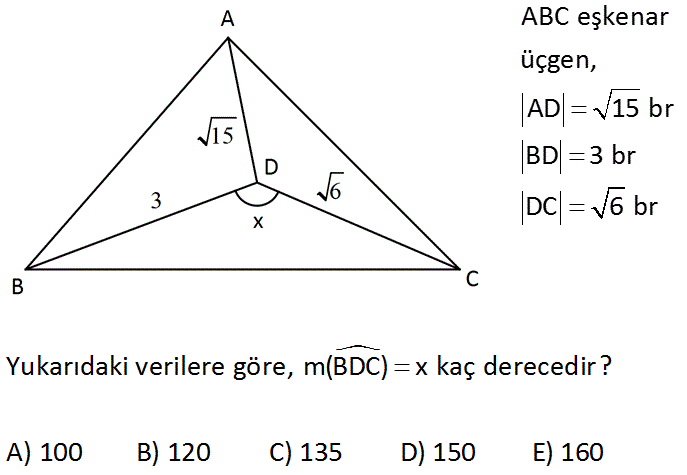
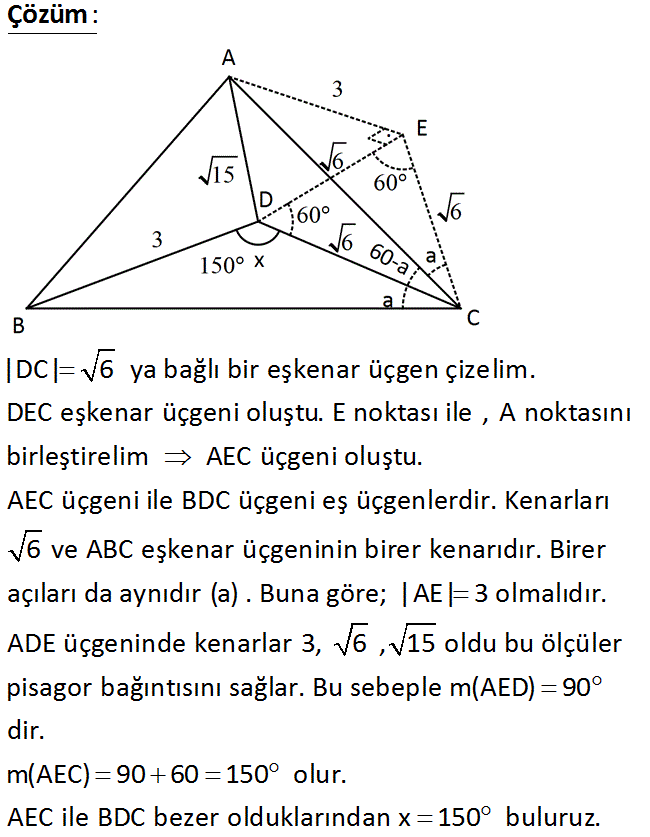
www.matematikkolay.net ABC eşkenar üçgen, AD 15 br BD 3 br DC 6 br Yukarıdaki verilere göre, m(BDC) x kaç derecedir? A) 100 B) 120 C) 135 D) 150 E) 160 : Çözüm |DC| 6 ya bağlı bir eşkenar üçgen çizelim. DEC eşkenar üçgeni oluştu. E noktası ile , A noktasını birleştirelim AEC üçgeni oluştu. AEC üçgeni ile BDC üçgeni eş üçgenlerdir. Kenarları 6 ve ABC eşkenar ü çgeninin birer kenarıdır. Birer açıları da aynıdır (a) . Buna göre; |AE| 3 olmalıdır. ADE üçgeninde kenarlar 3, 6 , 15 oldu bu ölçüler pisagor bağıntısını sağlar. Bu sebeple m(AED) 90 dir. m(AEC) 90 60 15 0 olur. AEC ile BDC bezer olduklarından x 150 buluruz. www.matematikkolay.net 20
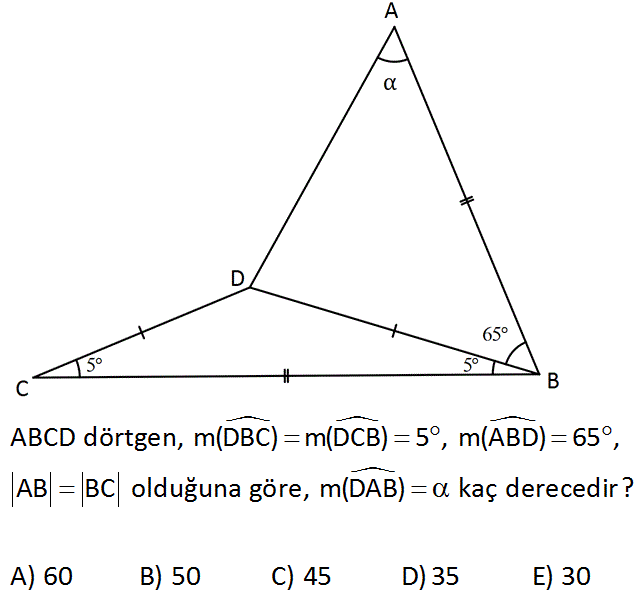
www.matematikkolay.net ABCD dörtgen, m(DBC) m(DCB) 5 , m(ABD) 65 , AB BC olduğuna göre, m(DAB) kaç derecedir? A) 60 B) 50 C) 45 D) 35 E) 30 : Çözüm www.matematikkolay.net HDB şeklinde bir eşkenar üçgen çizelim. Bu üçgenin bütün açıları 60 dir. m(HBA) 65 60 5 kalır. HBA üçgeni ile DBC üçgeninin ikişer kenarları aynı uzunlukta ve bu kenarlar arasındaki açı da 5 derece ol duğundan bu üçgenler eş üçgenlerdir. O halde m(HAB) m(DCB) 5 olmalıdır. HBA üçgeninin iç açıları toplamından; m(BHA) 170 dir. m(AHD) 360 170 60 130 dir. AHD üçgeni de bir ikizkenar üçgen olduğundan; 180 130 m(HAD) 25 dir. O halde; 2 25 5 30 buluruz. 46
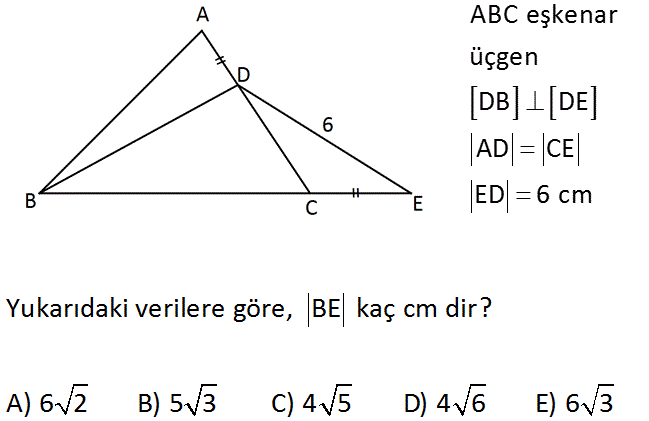
ABC eşkenar üçgen DB DE AD CE ED 6 cm Yukarıdaki verilere göre, BE kaç cm dir? A) 6 2 B) 5 3 C) 4 5 D) 4 6 E) 6 3 : Çözüm www.matematikkolay.net AD CE a olsun. DC b olsun. DFC eşkenar üçgenini ayırırsak; BF a olur. BFD üçgeni ile DCE üçgeninin iki kenarı ve bir açısı eş oldu. Bu iki üçgen eş üçgen olur. BDE üçgeni 45 45 90 üçgeni olur. BE 6 2 cm olu r. 65
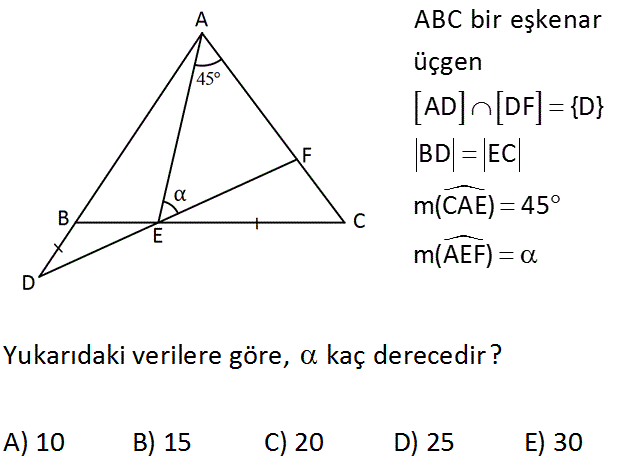
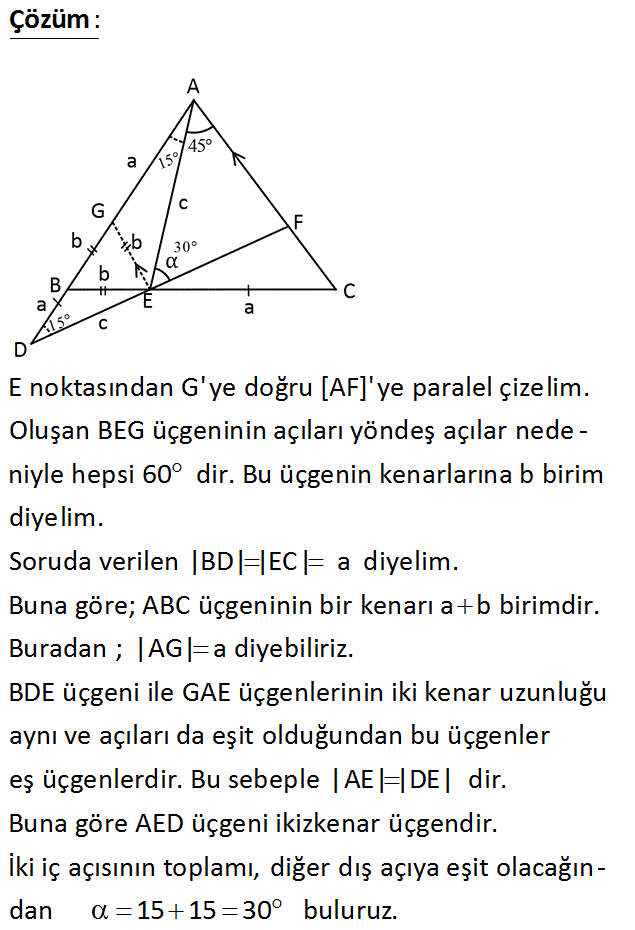
www.matematikkolay.net ABC bir eşkenar üçgen AD DF {D} BD EC m(CAE) 45 m(AEF) Yukarıdaki verilere göre, kaç derecedir? A) 10 B) 15 C) 20 D) 25 E) 30 : Çözüm E noktasından G’ ye doğru [AF]’ ye paralel çizelim. Oluşan BEG üçgeninin açıları yöndeş açılar nede – niyle hepsi 60 dir. Bu üçgenin kenarlarına b birim diyelim. Soruda verilen |BD| |EC| a diyelim. Buna g öre; ABC üçgeninin bir kenarı a b birimdir. Buradan ; |AG| a diyebiliriz. BDE üçgeni ile GAE üçgenlerinin iki kenar uzunluğu aynı ve açıları da eşit olduğundan bu üçgenler eş üçgenlerdir. Bu sebeple |AE| |DE| dir. Buna göre AED üçgeni ikizkenar üçgendir. İki iç açısının toplamı, diğer dış açıya eşit olacağın – dan 15 15 30 buluruz. www.matematikkolay.net 73
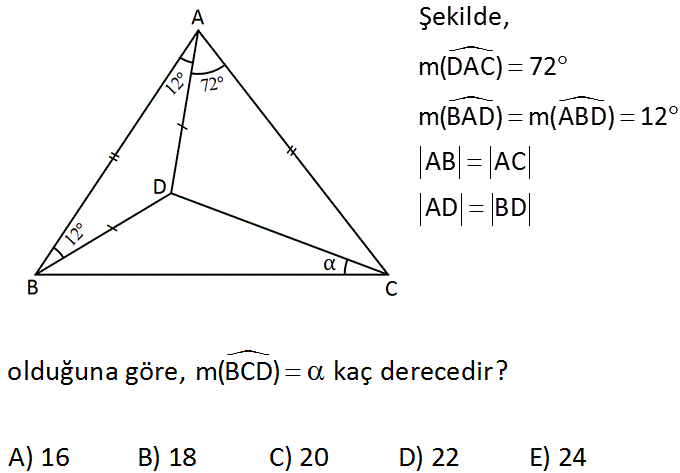
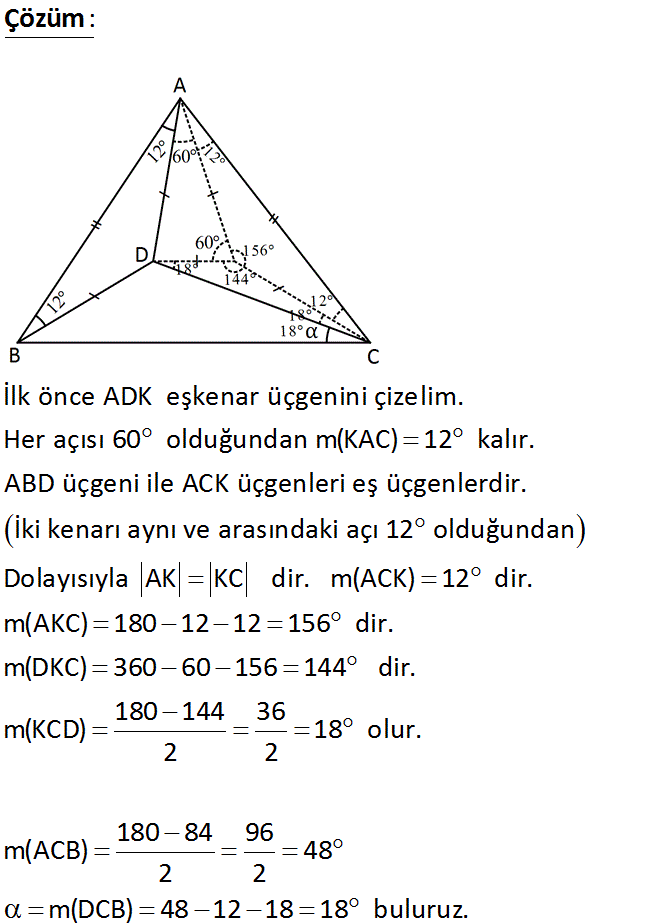
Şekilde, m(DAC) 72 m(BAD) m(ABD) 12 AB AC AD BD www.matematikkolay.net olduğuna göre, m(BCD) kaç derecedir? A) 16 B) 18 C) 20 D) 22 E) 24 : Çözüm www.matematikkolay.net İlk önce ADK eşkenar üçgenini çizelim. Her açısı 60 olduğundan m(KAC) 12 kalır. ABD üçgeni ile ACK üçgenleri eş üçgenlerdir. İki kenarı aynı ve arasındaki açı 12 olduğundan Dolayısıyla AK KC dir. m(ACK) 12 dir. m(AKC) 180 12 12 156 dir. m(DKC) 360 60 156 144 dir. 180 144 36 m(KCD) 18 olur. 2 2 180 84 96 m(ACB) 48 2 2 m(DCB) 48 12 18 18 buluruz. 76
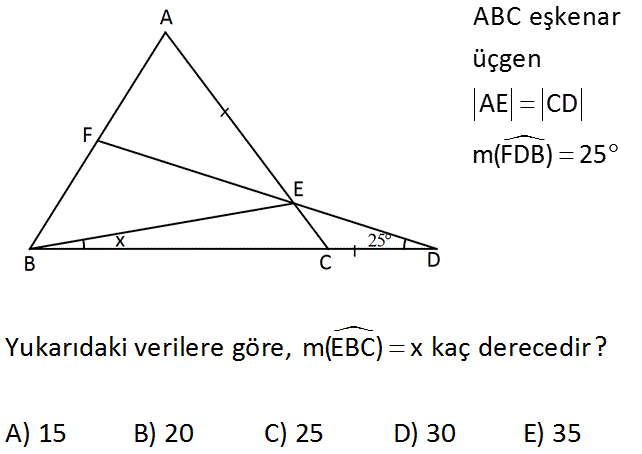
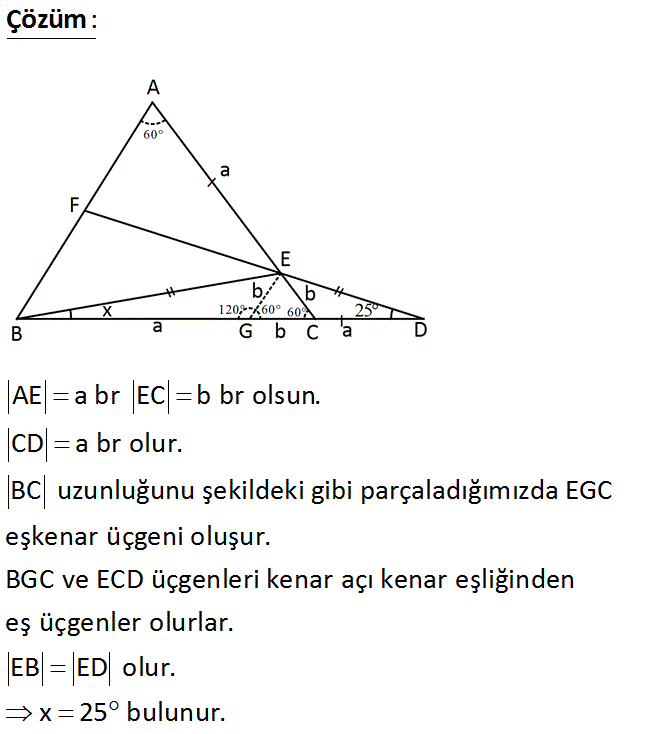
ABC eşkenar üçgen AE CD m(FDB) 25 www.matematikkolay.net Yukarıdaki verilere göre, m(EBC) x kaç derecedir? A) 15 B) 20 C) 25 D) 30 E) 35 : Çözüm AE a br EC b br olsun. CD a br olur. BC uzunluğunu şekildeki gibi parçaladığımızda EGC eşkenar üçgeni oluşur. BGC ve ECD üçgenleri kenar açı kenar eşliğinden eş üçgenler olurlar. EB ED olur. x 25 bulunur. 75

