Üçgen çizmeli açı soruları

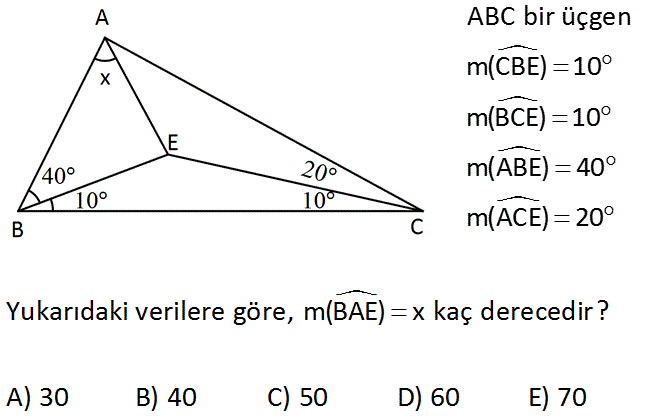
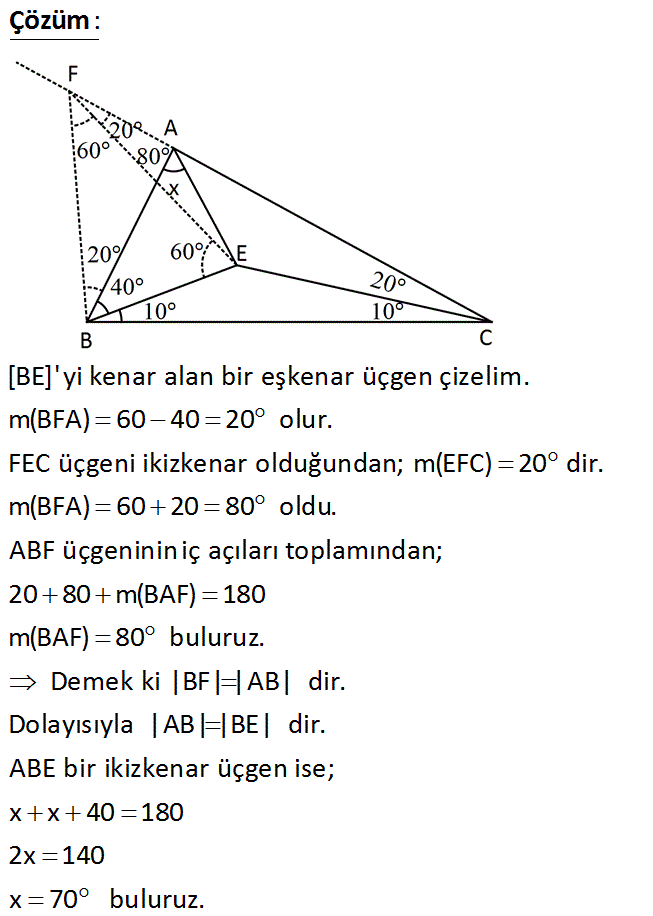
www.matematikkolay.net ABC bir ü çgen m(CBE) 10 m(BCE) 10 m(ABE) 40 m(ACE) 20 Yukarıdaki verilere göre, m(BAE) x kaç derecedir? A) 30 B) 40 C) 50 D) 60 E) 70 : Çözüm [BE]’yi kenar alan bir eşkenar üçgen çizelim. m(BFA) 60 40 20 olur. FEC üçgeni ikizkenar olduğundan; m(EFC) 20 dir. m(BFA) 60 20 80 oldu. ABF üçgenininiç açıları toplamından; 20 80 m(BAF) 180 m(BAF) 80  buluruz. Demek ki |BF| |AB| dir. Dolayısıyla |AB| |BE| dir. ABE bir ikizkenar üçgen ise; x x 40 180 2x 140 x 70 buluruz. www.matematikkolay.net 21
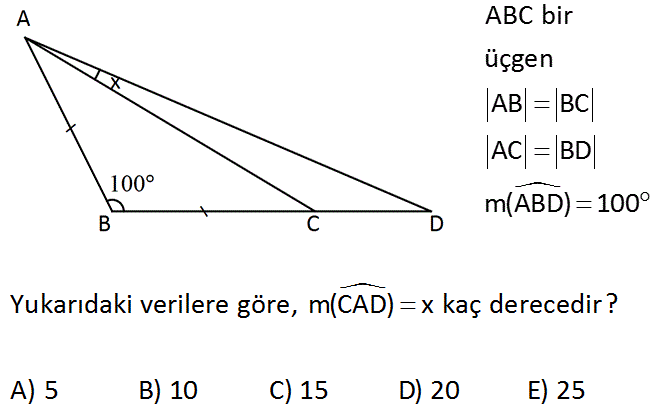
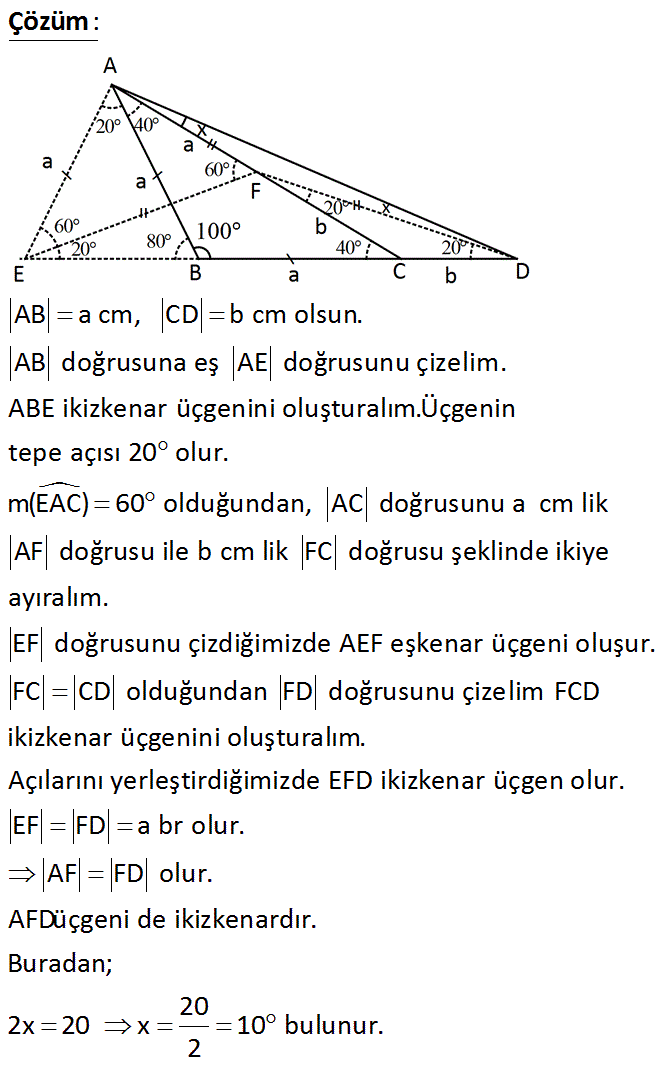
ABC bir üçgen AB BC AC BD m(ABD) 100 Yukarıdaki verilere göre, m(CAD) x kaç derecedir? A) 5 B) 10 C) 15 D) 20 E) 25 Çözüm: www.matematikkolay.net AB a cm, CD b cm olsun. AB doğrusuna eş AE doğrusunu çizelim. ABE ikizkenar üçgenini oluşturalım.Üçgenin tepe açısı 20 olur. m(EAC) 60 olduğundan, AC doğrusunu a cm lik AF doğrusu ile b cm lik FC doğru su şeklinde ikiye ayıralım. EF doğrusunu çizdiğimizde AEF eşkenar üçgeni oluşur. FC CD olduğundan FD doğrusunu çizelim FCD ikizkenar üçgenini oluşturalım. Açılarını yerleştirdiğimizde EFD ikizkenar üçgen olur. EF FD a br olur. AF FD olur. AFDüçgeni de ikizkenardır. Buradan; 20 2x 20 x 10 bulunur. 2 28
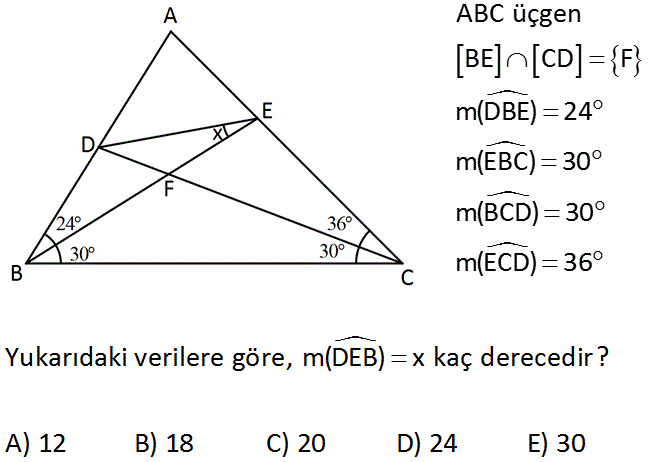
      ABC üçgen BE CD F m(DBE) 24 m(EBC) 30 m(BCD) 30 m(ECD) 36  Yukarıdaki verilere göre, m(DEB) x kaç derecedir? A) 12 B) 18 C) 20 D) 24 E) 30 Çözüm: www.matematikkolay.net KBF eşkenar üçgenini çizelim. |KD| a ve |DF| b olsun. m(KBF) 90 dir. BFC bir ikizkenar üçgen olduğundan, |FC| a b dir. KBD üçgeni ile FCE üçgeninin açıları aynıdır. Bir kenarları aynı olduğundan b unlar eş üçgenlerdir. Bu sebeple |KD| |FE| a dır. FME eşkenar üçgeni oluşturalım. Kenar uzunlukları a birimdir. |MC| b olur. EMC üçgeni ile EFD üçgeninin iki kenarı eşit (a ve b) ve bu iki kenar aras ındaki açı 120 dir. Buna göre bunlar eş üçgenlerdir. O halde, x m(MEC) 24 buluruz. 30
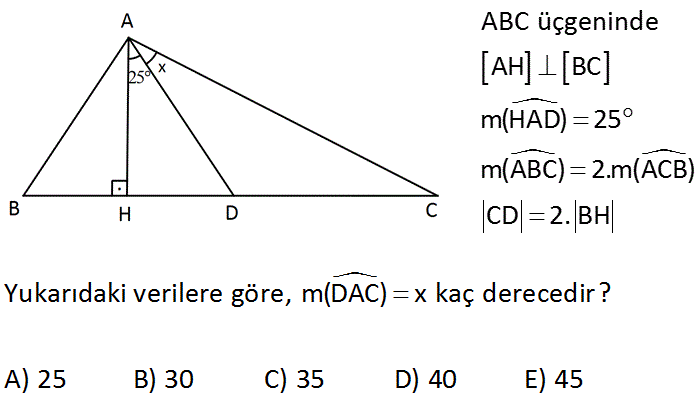
    ABC üçgeninde AH BC m(HAD) 25 m(ABC) 2.m(ACB) CD 2. BH  Yukarıdaki verilere göre, m(DAC) x kaç derecedir? A) 25 B) 30 C) 35 D) 40 E) 45 Çözüm: www.matematikkolay.net   m ACB a olsun. m ABC 2a olur. Dış açısı 2a olacak şekilde ikizkenar AEB üçgenini oluşturalım. AEC üçgeni ikizkenar olur. DC 2k, BH k olsun. HD t olsun. İkizkenar üçgende yükseklik tabanı 2 eş parçaya böler. HC  2k t EH 2k t olmalı. EB 2k t k k t olur. EAB üçgeninde muhteşem üçlü oluştuğundan, m EAD 90 olur. a 65 90 a 25 olur. ACD üçgeninde iki iç açı bir dış açıyı vereceğinden, x a 65 x 25 65 x 40 bulunur  . 37
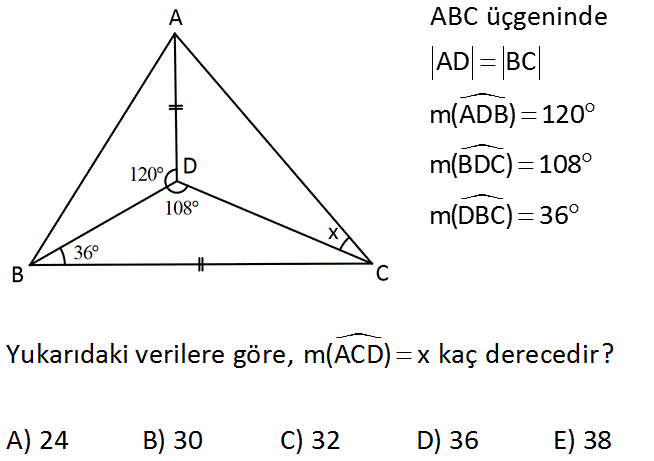
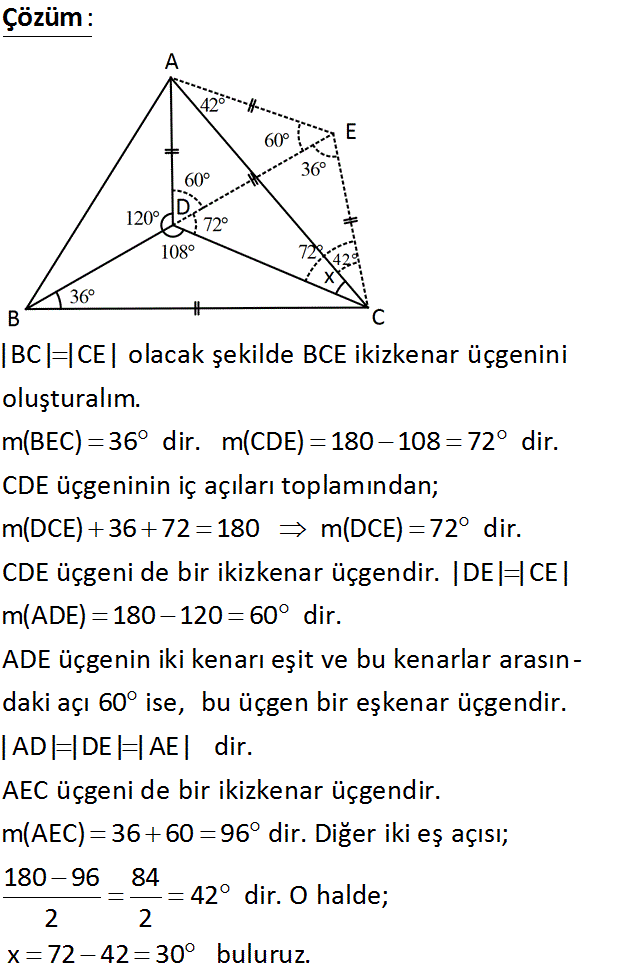
ABC üçgeninde AD BC m(ADB) 120 m(BDC) 108 m(DBC) 36 Yukarıdaki verilere göre, m(ACD) x kaç derecedir? A) 24 B) 30 C) 32 D) 36 E) 38 www.matematikkolay.net : Çözüm |BC| |CE| olacak şekilde BCE ikizkenar üçgenini oluşturalım. m(BEC) 36 dir. m(CDE) 180 108 72 dir. CDE üçgeninin iç açıları toplamından; m(DCE) 36 72 180 m(DCE) 72 dir. CDE üçgeni de bir ikizke  nar üçgendir. |DE| |CE| m(ADE) 180 120 60 dir. ADE üçgenin iki kenarı eşit ve bu kenarlar arasın – daki açı 60 ise, bu üçgen bir eşkenar üçgendir. |AD| |DE| |AE| dir. AEC üçgeni de bir ikizkenar üçg  endir. m(AEC) 36 60 96 dir. Diğer iki eş açısı; 180 96 84 42 dir. O halde; 2 2 x 72 42 30 buluruz.   39
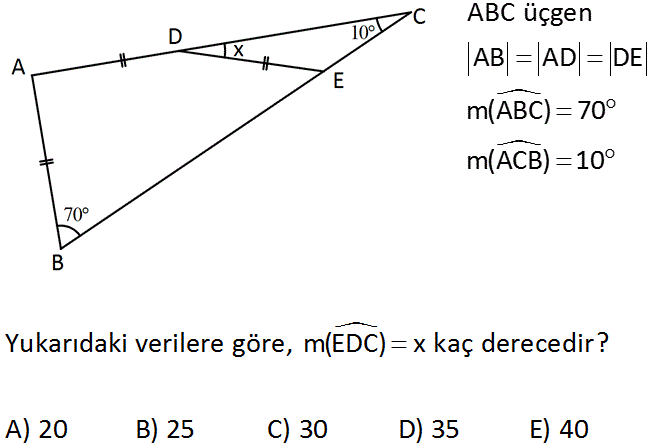
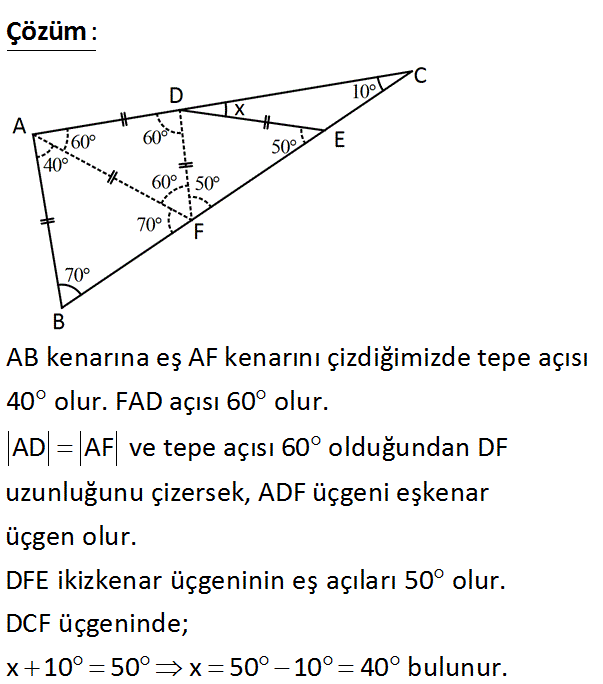
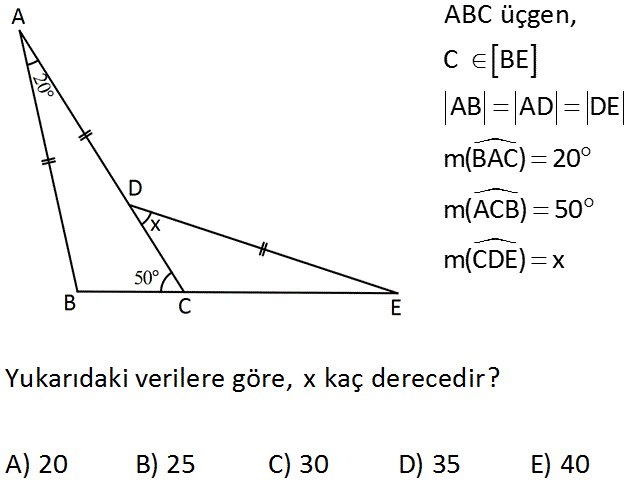
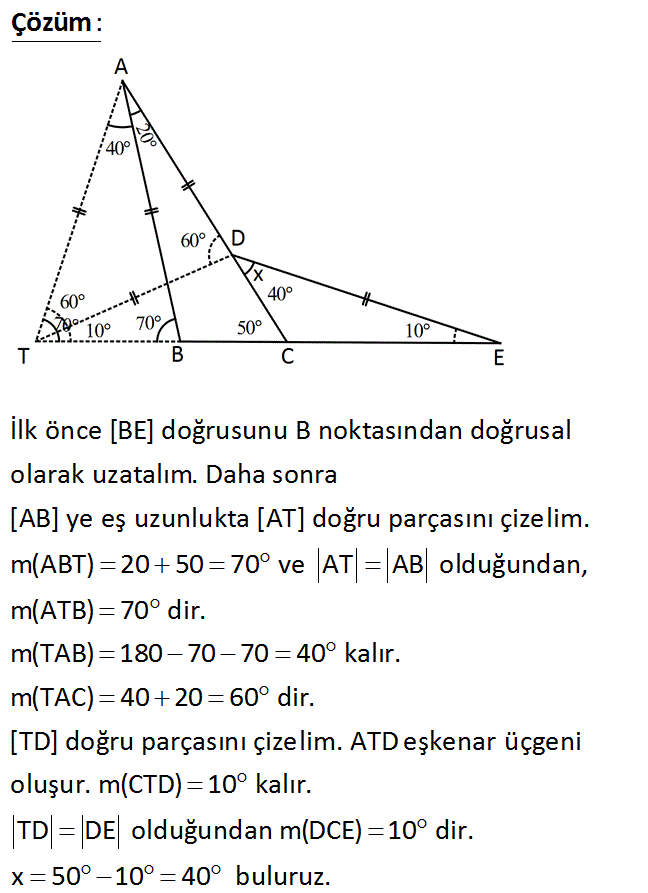
ABC üçgen AB AD DE m(ABC) 70 m(ACB) 10 Yukarıdaki verilere göre, m(EDC) x kaç derecedir? A) 20 B) 25 C) 30 D) 35 E) 40 www.matematikkolay.net : Çözüm AB kenarına eş AF kenarını çizdiğimizde tepe açısı 40 olur. FAD açısı 60 olur. AD AF ve tepe açısı 60 olduğundan DF uzunluğunu çizersek, ADF üçgeni eşkenar üçgen olur. DFE ikizkenar üçgeninin eş açılar ı 50 olur. DCF üçgeninde; x 10 50 x 50 10 40 bulunur.  42
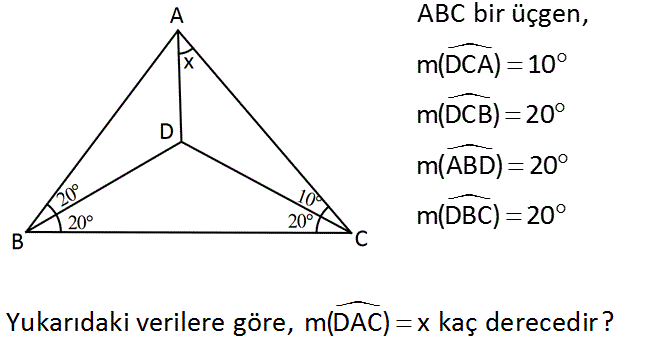
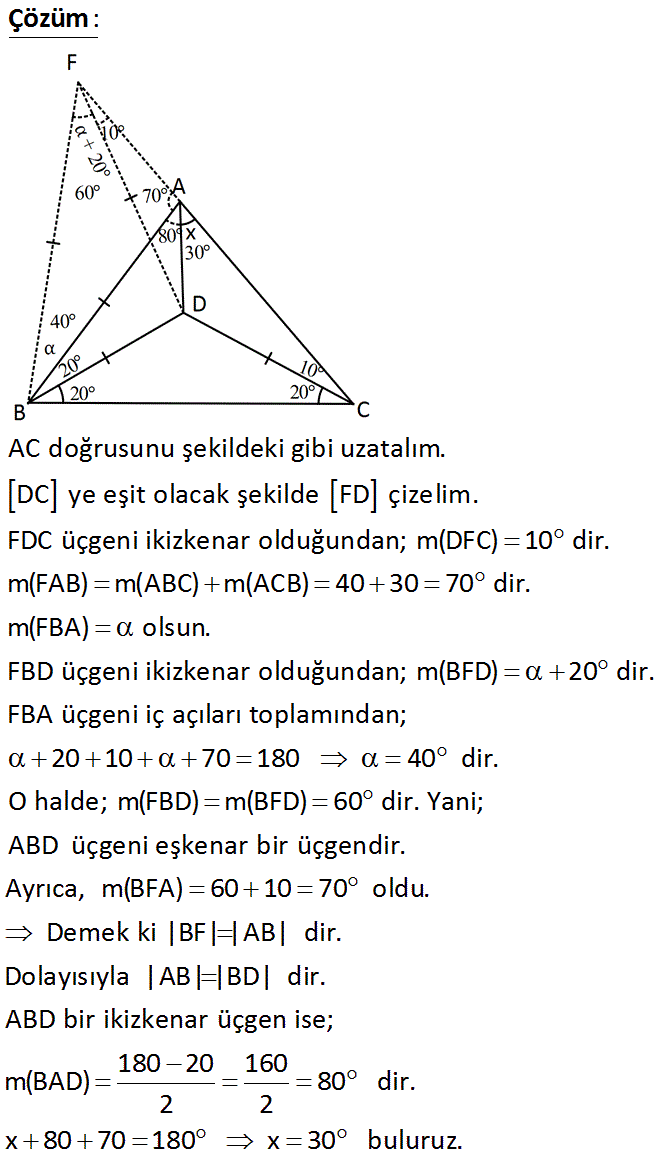
ABC bir üçgen, m(DCA) 10 m(DCB) 20 m(ABD) 20 m(DBC) 20 Yukarıdaki verilere göre, m(DAC) x kaç derecedir? www.matematikkolay.net : Çözüm     AC doğrusunu şekildeki gibi uzatalım. DC ye eşit olacak şekilde FD çizelim. FDC üçgeni ikizkenar olduğundan; m(DFC) 10 dir. m(FAB) m(ABC) m(ACB) 40 30 70 dir. m(FBA) olsun. FBD üçgeni ikizkenar olduğu ndan; m(BFD) 20 dir. FBA üçgeni iç açıları toplamından; 20 10 70 180 40 dir. O halde; m(FBD) m(BFD) 60 dir. Yani; ABD üçgeni eşkenar bir üçgendir. Ayrıca, m(BFA) 60 10 70 oldu. Demek ki |BF| |AB| dir. Dolayısıyla |AB| |BD| dir. ABD bir ikizkenar üçgen ise; 180 20 160 m(BAD) 80 dir. 2 2 x 80 70 180 x 30 buluruz.  www.matematikkolay.net 54
www.matematikkolay.net   ABC üçgen, C BE AB AD DE m(BAC) 20 m(ACB) 50 m(CDE) x  Yukarıdaki verilere göre, x kaç derecedir? A) 20 B) 25 C) 30 D) 35 E) 40 : Çözüm ADC üçgeninin iç açıları toplamı 180 dir. m(ACD) 180 90 50 40 dir. Açıortay olduğundan; m(ACB) 40 40 80 dir. ABC üçgeninin iç açıları toplamından; 30 80 50 180 160 180 20 buluruz.   56