Soru Sor sayfası kullanılarak Üçgende Açıortay konusu altında Dış teğet çemberinin merkezi ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
2.SORU

3.SORU
4.SORU
Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
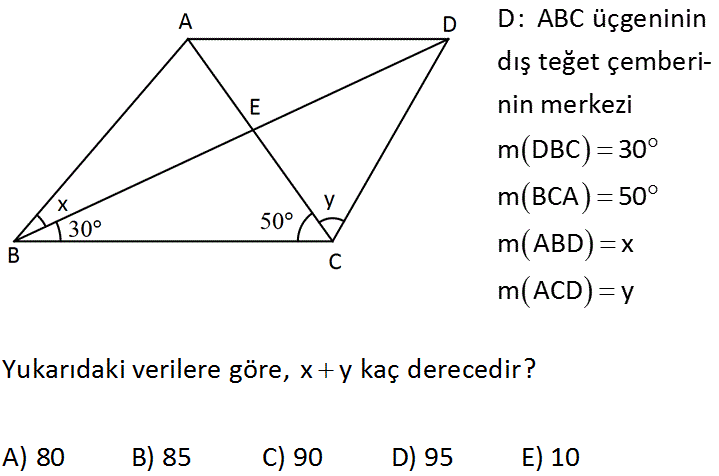
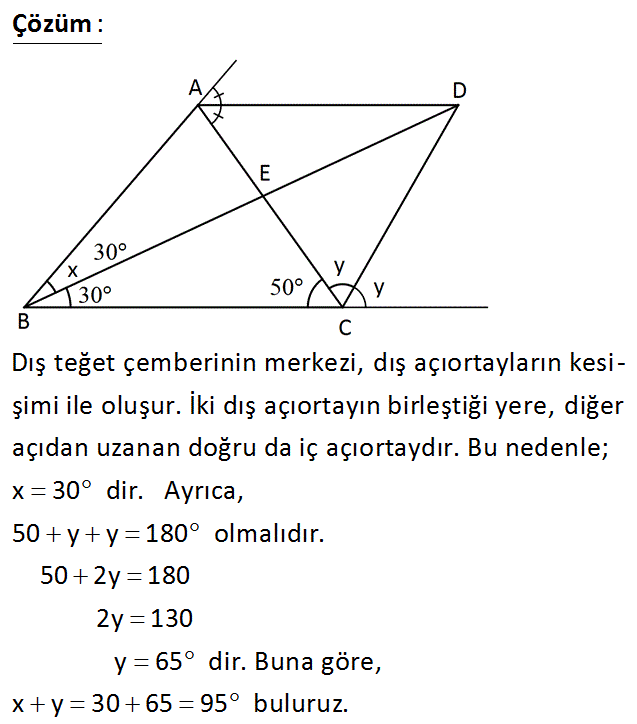
D: ABC üçgeninin dış teğet çemberinin merkezi m DBC 30 m BCA 50 m ABD x m ACD y Yukarıdaki verilere göre, x y kaç derecedir? A) 80 B) 85 C) 90 D) 95 E) 10 Dış teğet çemberinin merkezi, dış açıortayların kesi – şimi ile oluşur. İki dış açıortayın birleştiği yere, diğer açıdan uzanan doğru da iç açıortaydır. Bu nedenle; x 30 ve y 50 dir. Topl mla : a Çözüm rı da 80 dir. 25
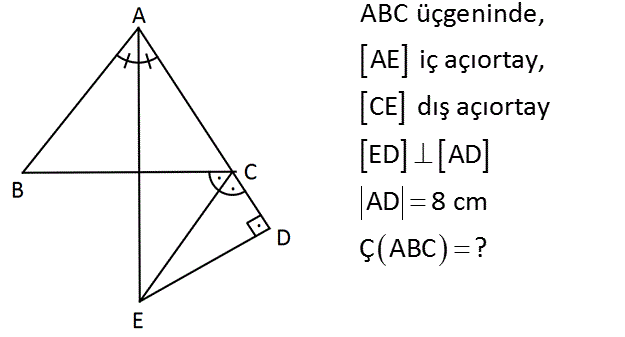
ABC üçgeninde, AE iç açıortay, CE dış açıortay ED AD AD 8 cm Ç ABC ? Çözüm: B köşesinden , E noktasına doğru çizdiğimizde, bu doğru da bir açıortay olur. Çünkü İki dış açıortay ile bir iç açıortay tek bir noktada kesişir. Açıortaydan inilen dikmeler birbirine eşit olduğu gibi, kolları da birbirine eşittir. Bu nedenle; |AF| |AD| 8 cm dir. Şekildeki gibi dikmelerin ayırdığı uzunluklara a ve b diyebiliriz. Buradan üçgenin çevresini; 8 a a b 8 b 16 buluruz. 15
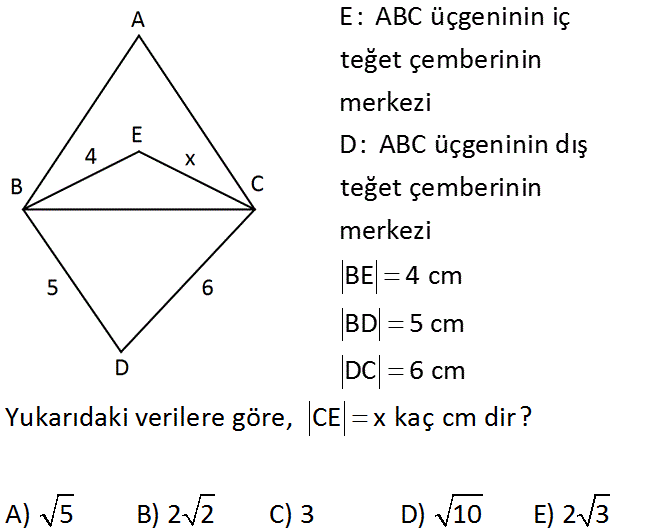
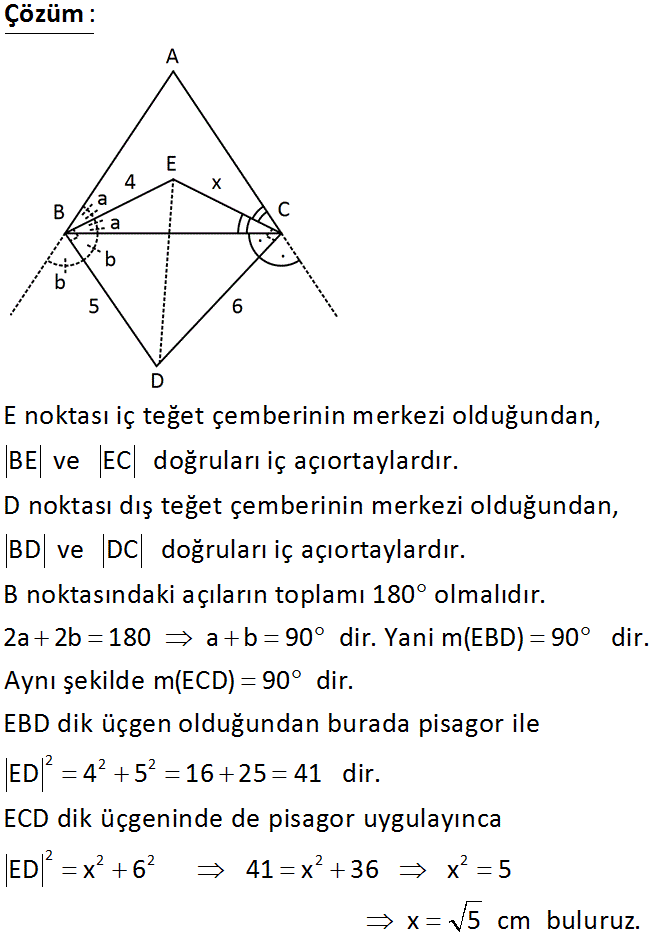
E: ABC üçgeninin iç teğet çemberinin merkezi D: ABC üçgeninin dış teğet çemberinin merkezi BE 4 cm BD 5 cm DC 6 cm Yukarıdaki verilere göre, CE x kaç cm dir? A) 5 B) 2 2 C) 3 D) 10 E) 2 3 : Çözüm E noktası iç teğet çemberinin merkezi olduğundan, BE ve EC doğruları iç açıortaylardır. D noktası dış teğet çemberinin merkezi olduğundan, BD ve DC doğruları iç açıortaylardır. B noktasındaki açıların 2 2 2 toplamı 180 olmalıdır. 2a 2b 180 a b 90 dir. Yani m(EBD) 90 dir. Aynı şekilde m(ECD) 90 dir. EBD dik üçgen olduğundan burada pisagor ile ED 4 5 16 25 41 dir. ECD dik üçgeninde de pisagor uy 2 2 2 2 2 gulayınca ED x 6 41 x 36 x 5 x 5 cm buluruz. 47
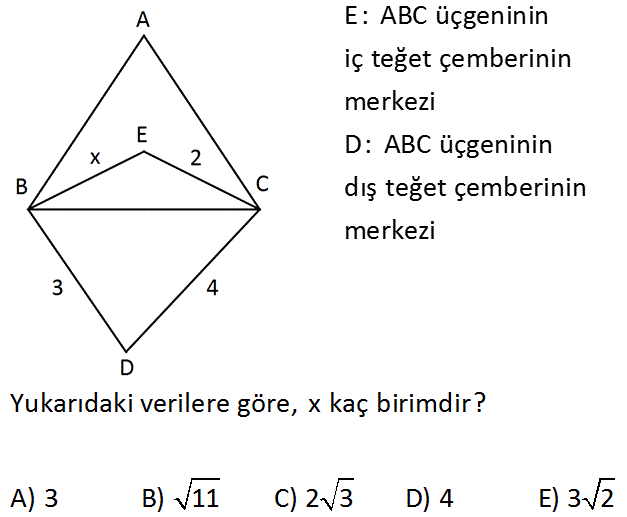
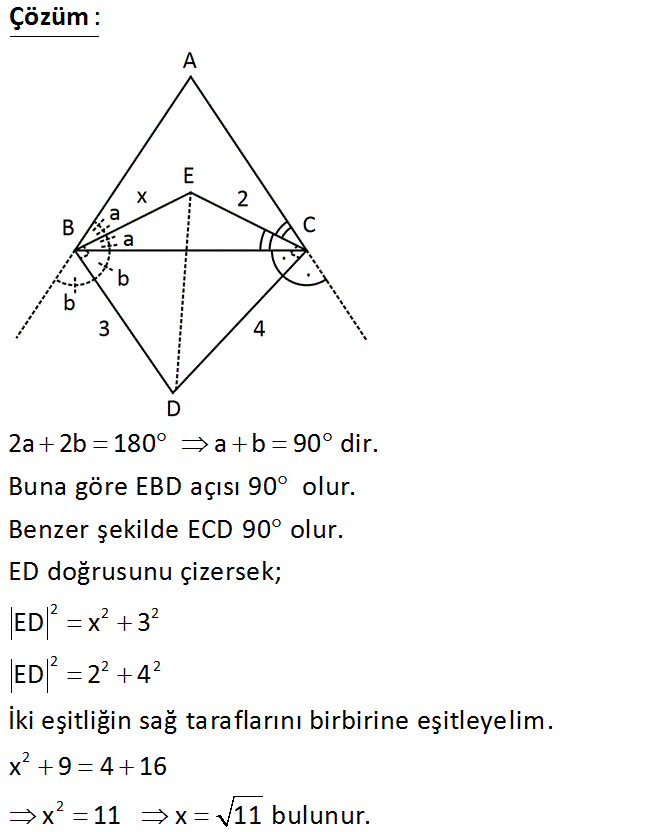
E: ABC üçgeninin iç teğet çemberinin merkezi D: ABC üçgeninin dış teğet çemberinin merkezi Yukarıdaki verilere göre, x kaç birimdir? A) 3 B) 11 C) 2 3 D) 4 E) 3 2 : Çözüm 2 2 2 2 2 2 2 2 2a 2b 180 a b 90 dir. Buna göre EBD açısı 90 olur. Benzer şekilde ECD 90 olur. ED doğrusunu çizersek; ED x 3 ED 2 4 İki eşitliğin sağ taraflarını birbirine eşitleyelim. x 9 4 16 x 11 x 11 bul unur. 39

