Soru Sor sayfası kullanılarak Polinomlar konusu altında Polinom Bölmesi ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
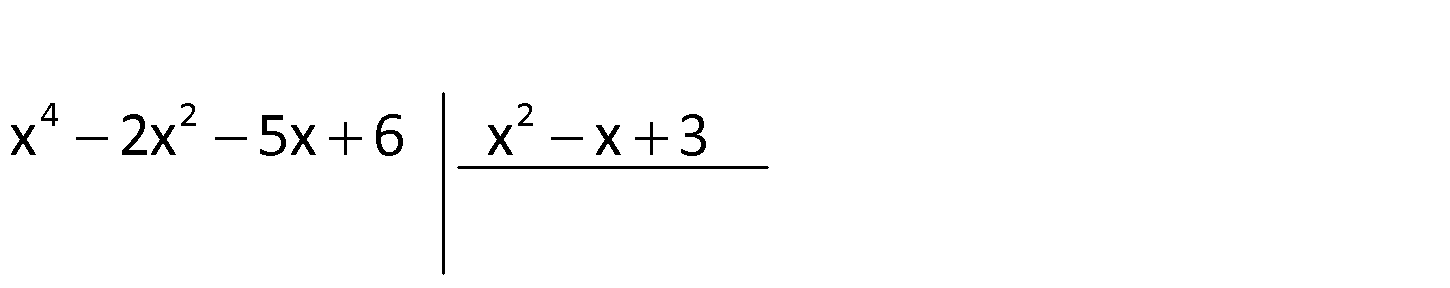
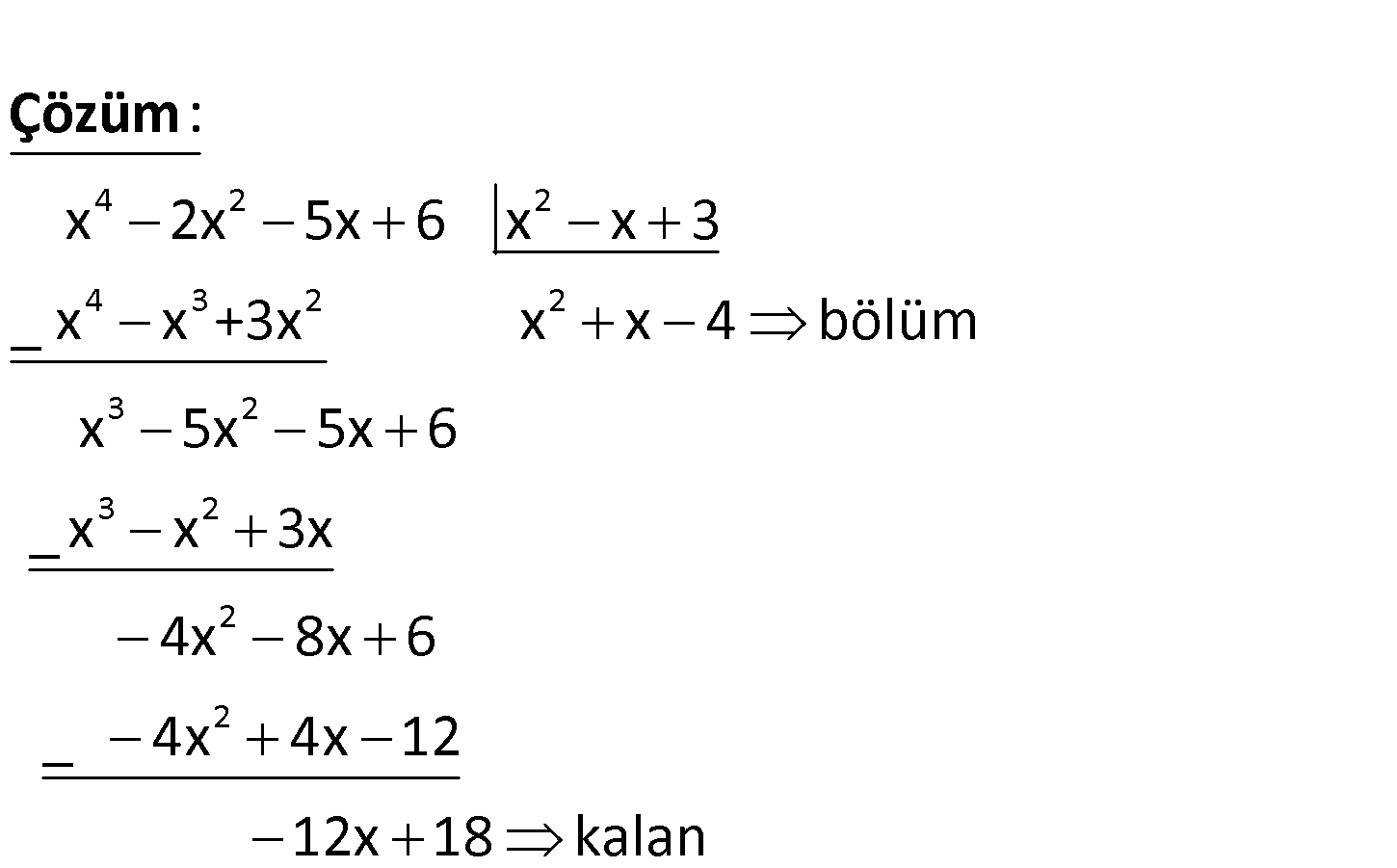
2.SORU
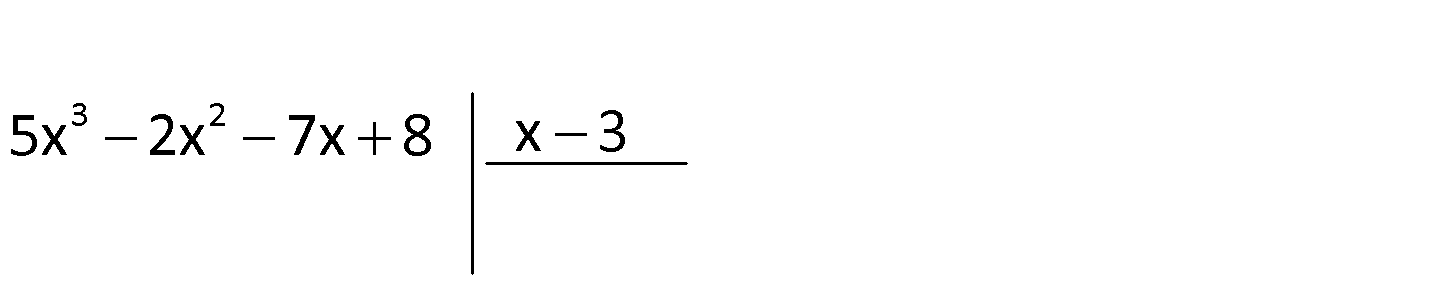
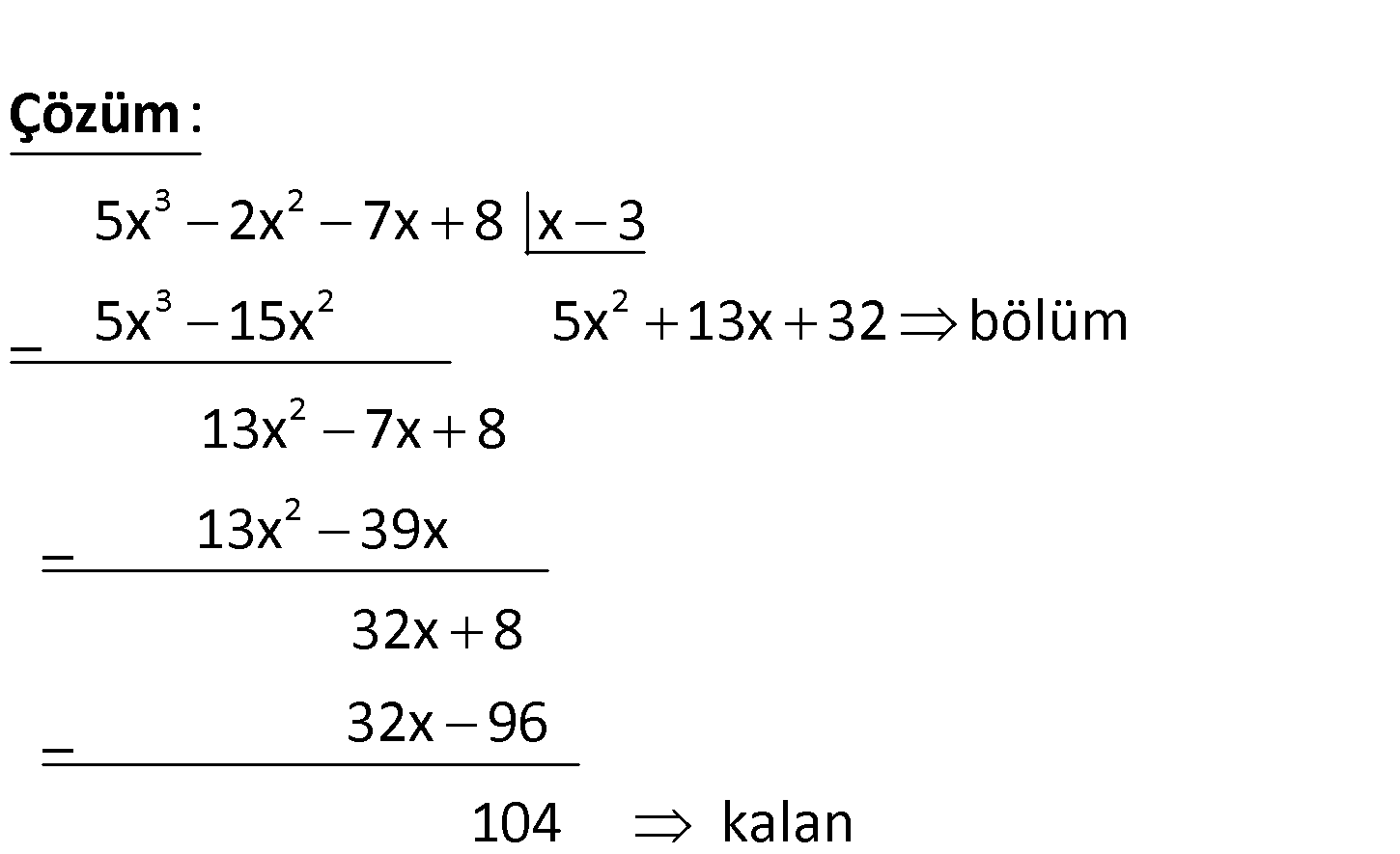
3.SORU


4.SORU


5.SORU

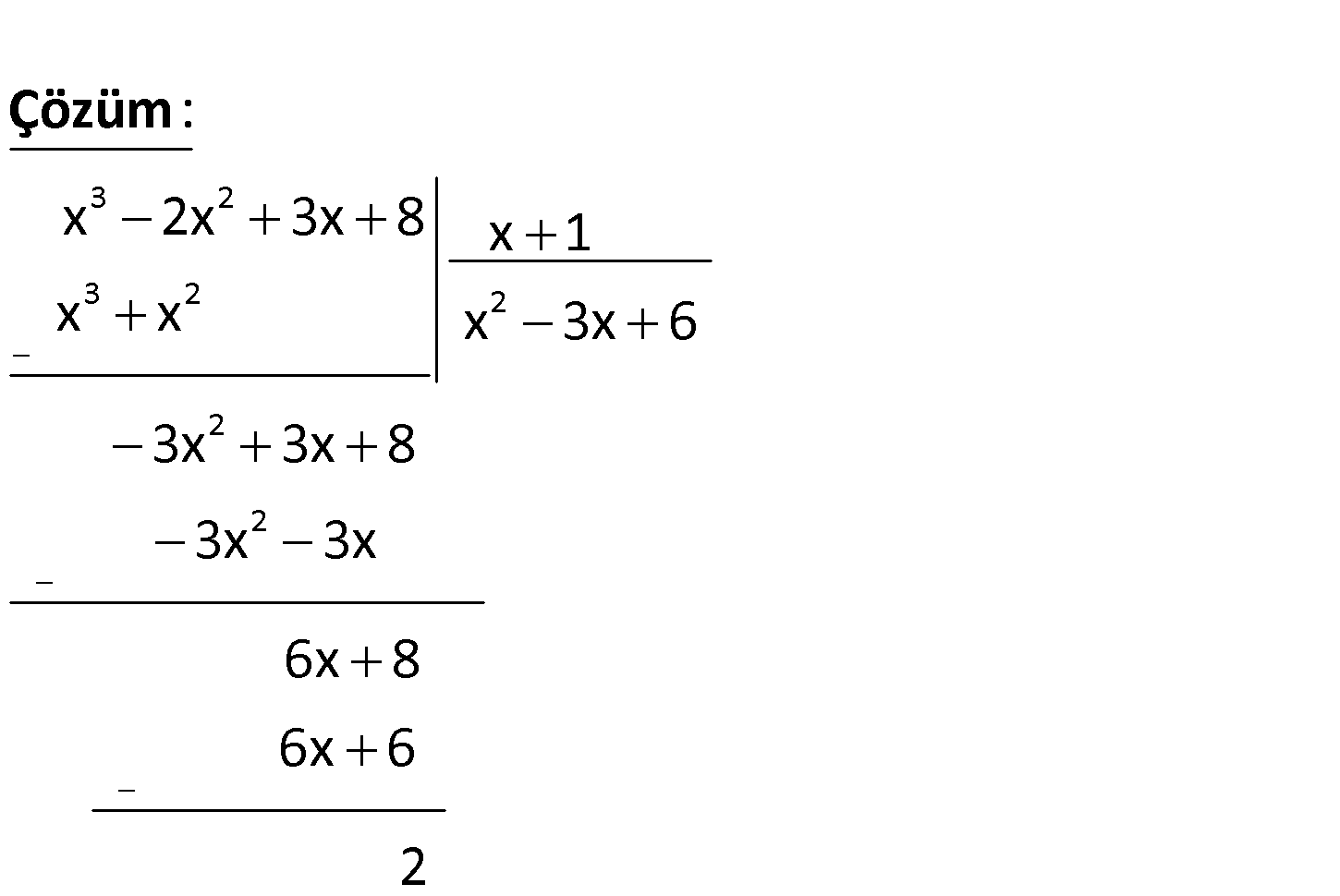
6.SORU


7.SORU
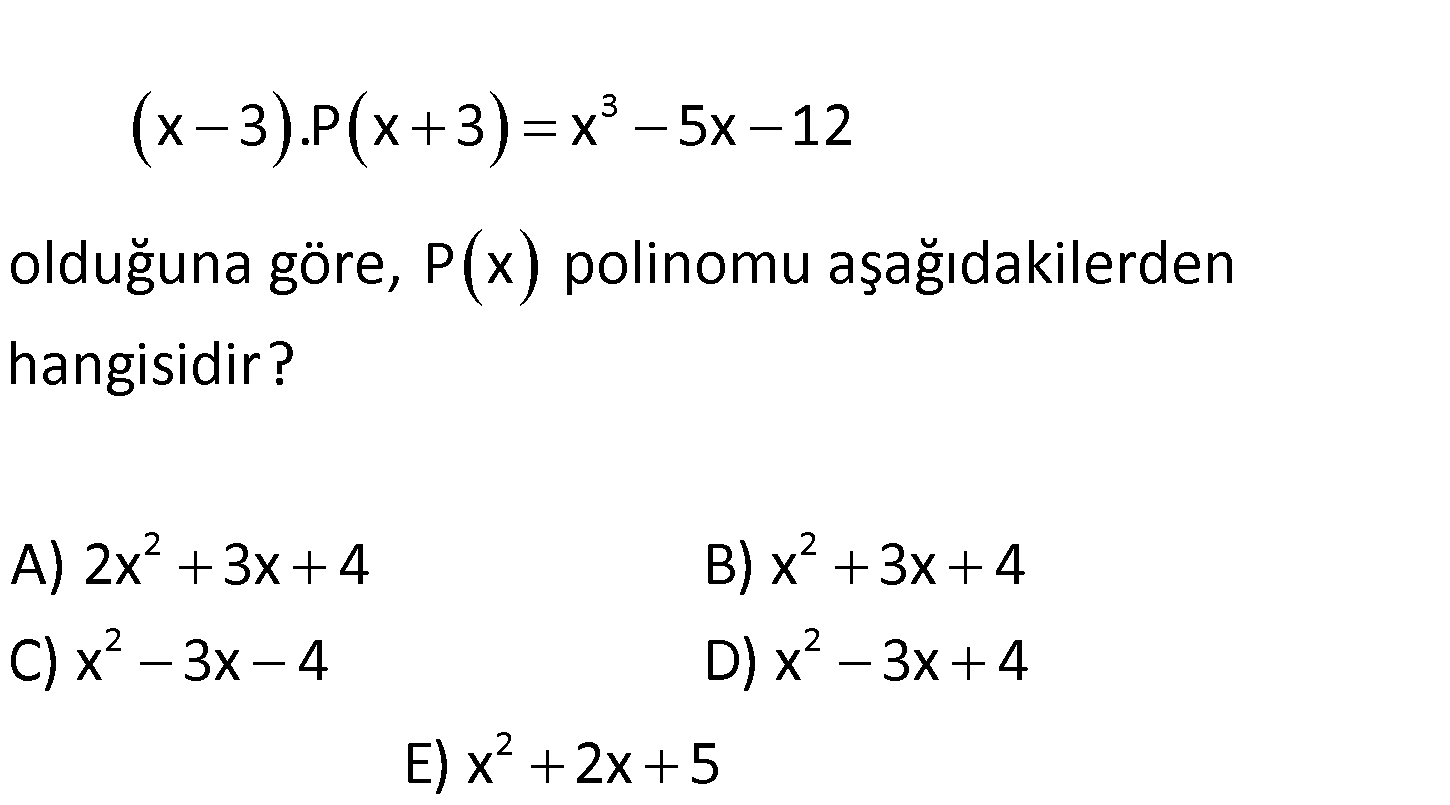

Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
4 2 2 x 2x 5x 6 x x 3 4 2 2 4 3 2 2 3 2 3 2 x 2x 5x 6 x x 3 _ x x +3x x x 4 bölüm x 5x 5x 6 _ x x 3x : Çözüm 2 2 4x 8x 6 _ 4x 4x 12 12x 18 kalan www.matematikkolay.net 10
3 2 5x 2x 7x 8 x 3 3 2 3 2 2 2 5x 2x 7x 8 x 3 _ 5x 15x 5x 13x 32 bölüm 13x 7x 8 _ : Çözüm 2 13x 39x 32x 8 _ 32x 96 104 kalan 11
P x polinomu başkatsayısı a olan 4. dereceden bir polinomdur. Buna göre, P 2x 1 polinomunun P x ile bölümünden elde edilen bölüm aşağıdakilerden hangi – sidir? A) 4 B) 8 C) 8a D) 16 E) 16a www.matematikkolay.net 4 4 4 4 P x ax gibi bir polinom olsun. P(2x 1) a 2x 1 olur. a 16x …. 16ax …. bu pol : in Çözüm 4 omu ax ‘e bölersek; Bölüm 16a olur. 32
www.matematikkolay.net P x üçüncü dereceden bir polinom olmak üzere, P 4x 1 polinomunun P x 2 ile bölümünden elde edilen bölüm aşağıdakilerden hangisidir? A) 4 B) 16 C) 32 D) 64 E) 80 3. dereceden bir polinomu yine 3. dereceden bir polinoma bölersek; bölüm sabit bir sayı : olur. Çözüm 3 3 3 3 3 3 3 3 Bu sabit sayı baş katsayıların oranına eşittir. P x ax olsun. P 4x 1 a 4x 1 64ax … P x 2 a x 2 ax … 64ax … ax … -64ax … 64 bölüm. 85
3 2 x 2x 3x 8 polinomunun x 1 polinomuna bölümünden elde edilen bölümü bulunuz. 3 2 3 2 2 2 2 x 2x 3x 8 x 1 x x x 3x 6 3x 3x 8 3x 3x : Çözüm 6x 8 6x 6 2 110
www.matematikkolay.net P x x 3 Q x x 2 Q x R x 2 3 Bölme işlemleri veriliyor. Buna göre, P 2 2 2 x polnomunun x x 6 ile bölümünden kalan aşağıdakilerden hangisidir? A) R x B) x x 6 .R x C) x x 6 D) 3x 7 E) x 2 Q(x) R(x).(x 2) 3 P(x) Q(x).(x 3) 2 Q(x) yerine yukarıdaki denklemi yazalım. P(x : ) R(x).(x 2) Çözüm 2 2 Bu kısım tam bölünür. Kalan 3 .(x 3) 2 P(x) R(x)(x x 6) 3x 9 2 P(x) R(x)(x x 6) 3x 7 Kalan 3x 7 buluruz. 151
www.matematikkolay.net 3 2 2 x 3 .P x 3 x 5x 12 olduğuna göre, P x polinomu aşağıdakilerden hangisidir? A) 2x 3x 4 B) x 3x 2 2 2 4 C) x 3x 4 D) x 3x 4 E) x 2x 5 3 9x 4x 3 2 İki kare farkı (x 3).P(x 3) x 5x 12 (x 3).P(x 3) x 9x 4x 12 (x 3).P(x 3) x ) 4(x : (x 9 Çözüm 3) (x 3).P(x 3) x(x 3)(x 3) 4(x 3) (x 3) .P(x 3) (x 3) 2 x.(x 3) 4 P(x 3) x.(x 3) 4 x yerine x 3 yazarak P(x)’i bulalım. P(x) (x 3).(x) 4 P(x) x 3x 4 buluruz. www.matematikkolay.net 100


3. Soruda 16 çıkması gerektiğini düşünüyorum.
Uyarınız için teşekkürler. Hata düzeltildi.