Soru Sor sayfası kullanılarak Parabol konusu altında Parabol ile doğrunun teğet olması ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
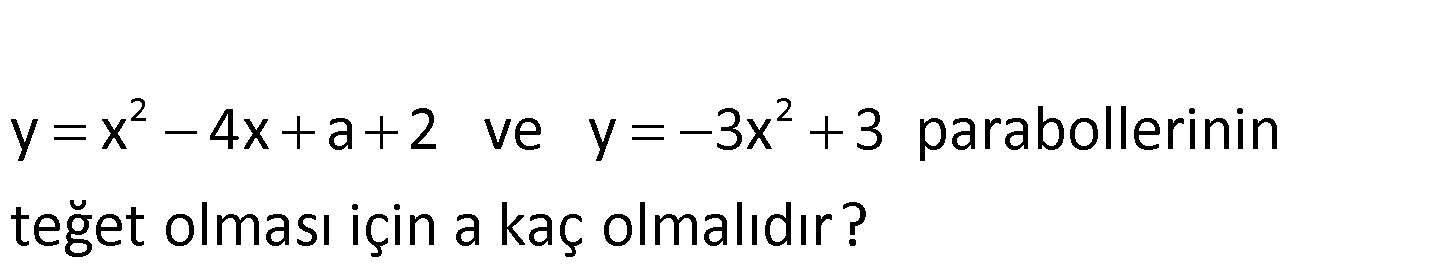

2.SORU
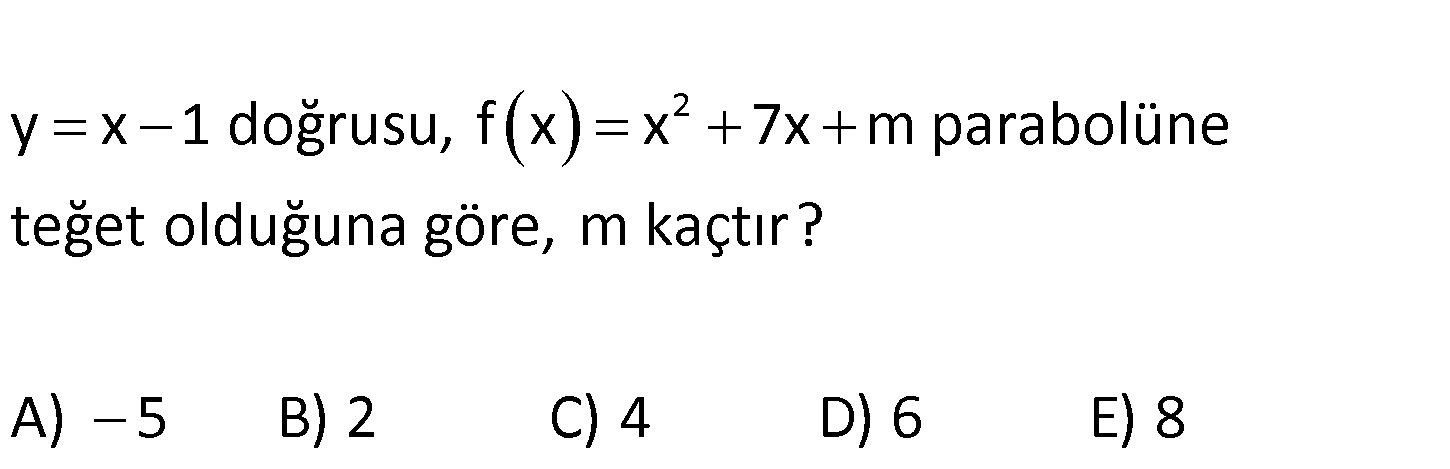

3.SORU


4.SORU


5.SORU
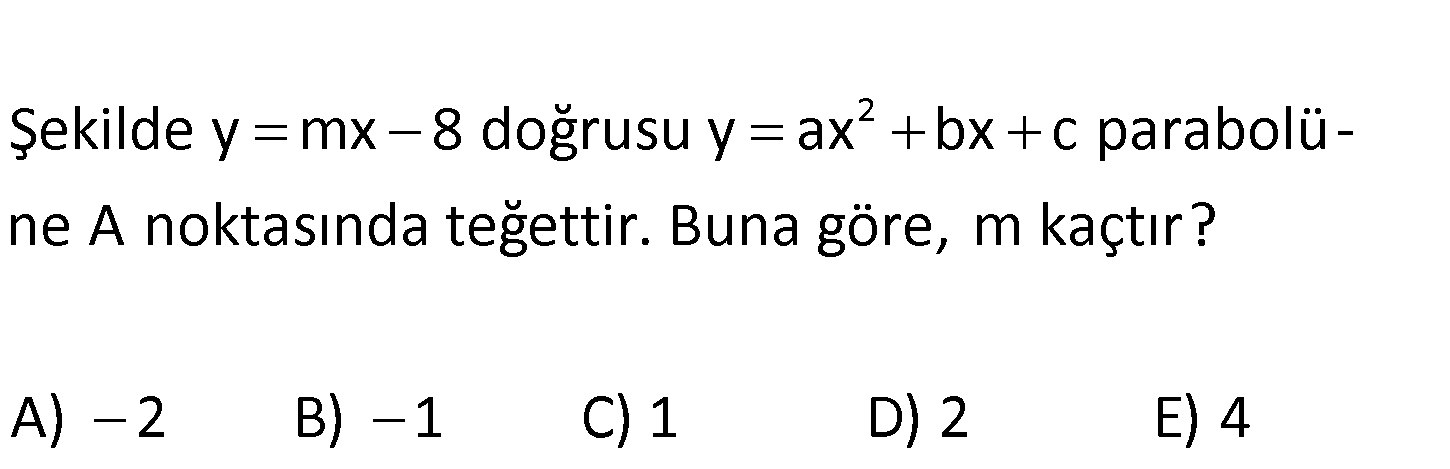

6.SORU
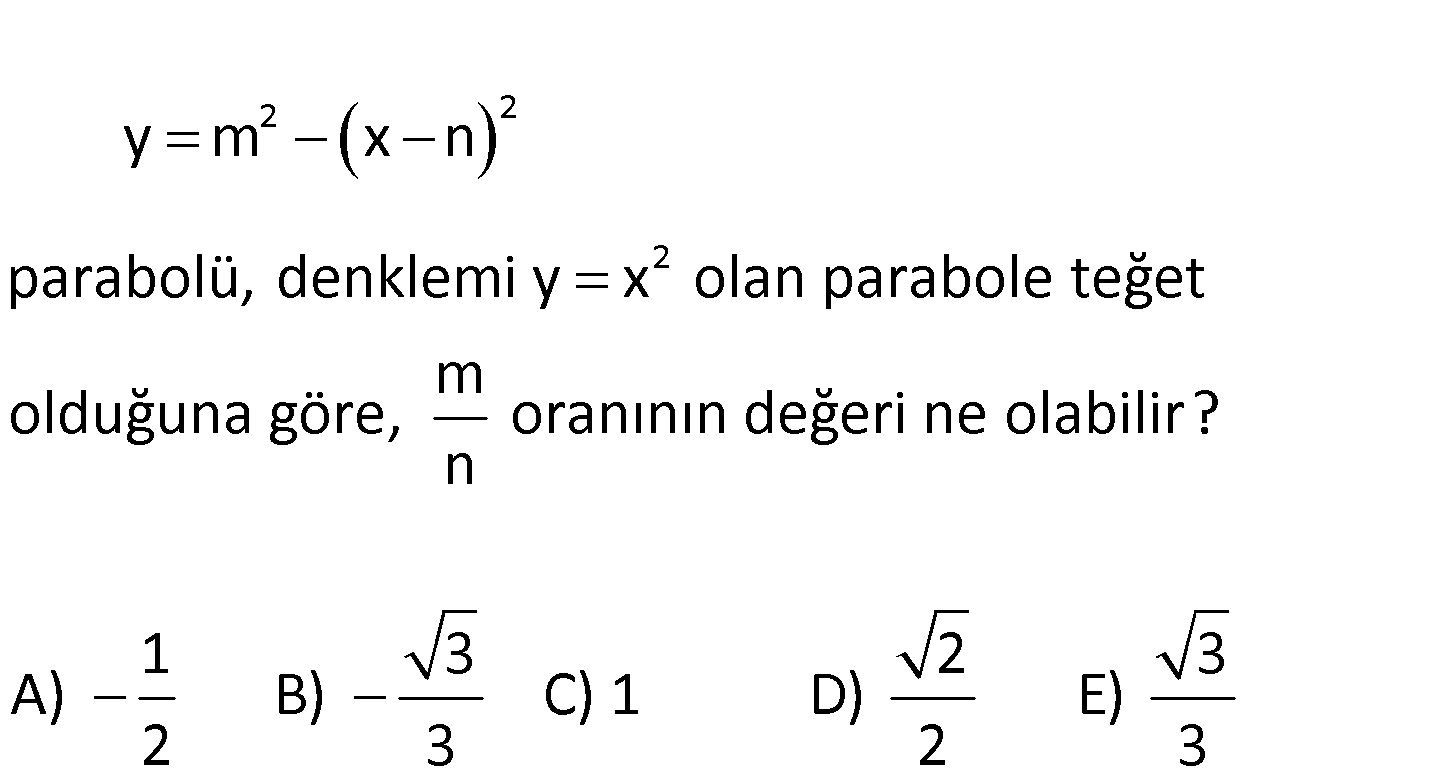

7.SORU



Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Çıkmış Sorular İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
2 2 y x 4x a 2 ve y 3x 3 parabollerinin teğet olması içi n a kaç olmalıdır? www.matematikkolay.net 2 2 2 a b Denklemleri birbirine eşitledikten sonra ; 0 olmalıdır. Buna göre; x 4x a 3x 3 x 4 : 2 4 Çözüm c 2 x a 1 0 0 olmalıdır. b 4ac 0 16 4.( 4)(a 1) 0 16 16a 16 0 16a 0 a 0 buluruz. 12
www.matematikkolay.net 2 y x 1 doğrusu, f x x 7x m parabolüne teğet olduğuna göre, m kaçtır? A) 5 B) 2 C) 4 D) 6 E) 8 2 2 y x 1 doğrusu, f(x) x 7x m parabolüne teğet ise parabol ile tek bir noktada kesişir : . x 7x m Çözüm 2 2 x 1 x 6x (m 1) 0 0 olmalı. b 4ac 0 36 4.(m 1) 0 36 9 4 .(m1) m1 9 m 8 bulunur. 37
2 x Denklemi, f x olan parabol m nin hangi m değeri için y x 2 doğrusuna teğettir? A) 8 B) 6 C) 4 D) 2 E) 1 www.matematikkolay.net İki fonksiyonun birbirine teğet ise, bunları birbirine eşitlediğimizde çözüm kümesi tek : olmal Çözüm 2 2 2 2 2 2 2 ıdır. Yani 0 olmalıdır. x x 2 eşitliğini kuralım. m x mx 2m x mx 2m 0 ‘ya bakalım. b 4ac m 4.1.2m 0 m 8m 0 m m 8 0 m 8 dir. x m 0 olamaz. parabolünü tanımsız m yapar. Cevap: A 56
2 y x 2x 4 parabolünün teğetlerinden biri y 4x m ise m kaçtır? A) 5 B) 4 C) 1 D) 4 E) 5 www.matematikkolay.net İki denklemi birbirine eşitlediğimizde 0 olmalıdır. y 4x m ise y 4x m yazalım. Şimd i : i ki Çözüm 2 2 2 y değerini birbirine eşitleyelim. x 2x 4 4x m x 6x 4 m 0 Şimdi de yı inceleyelim. 0 olmalı 6 4.1. 4 m 0 36 4 4 m 0 36 16 4m 0 20 4m 0 m 5 buluruz. 74
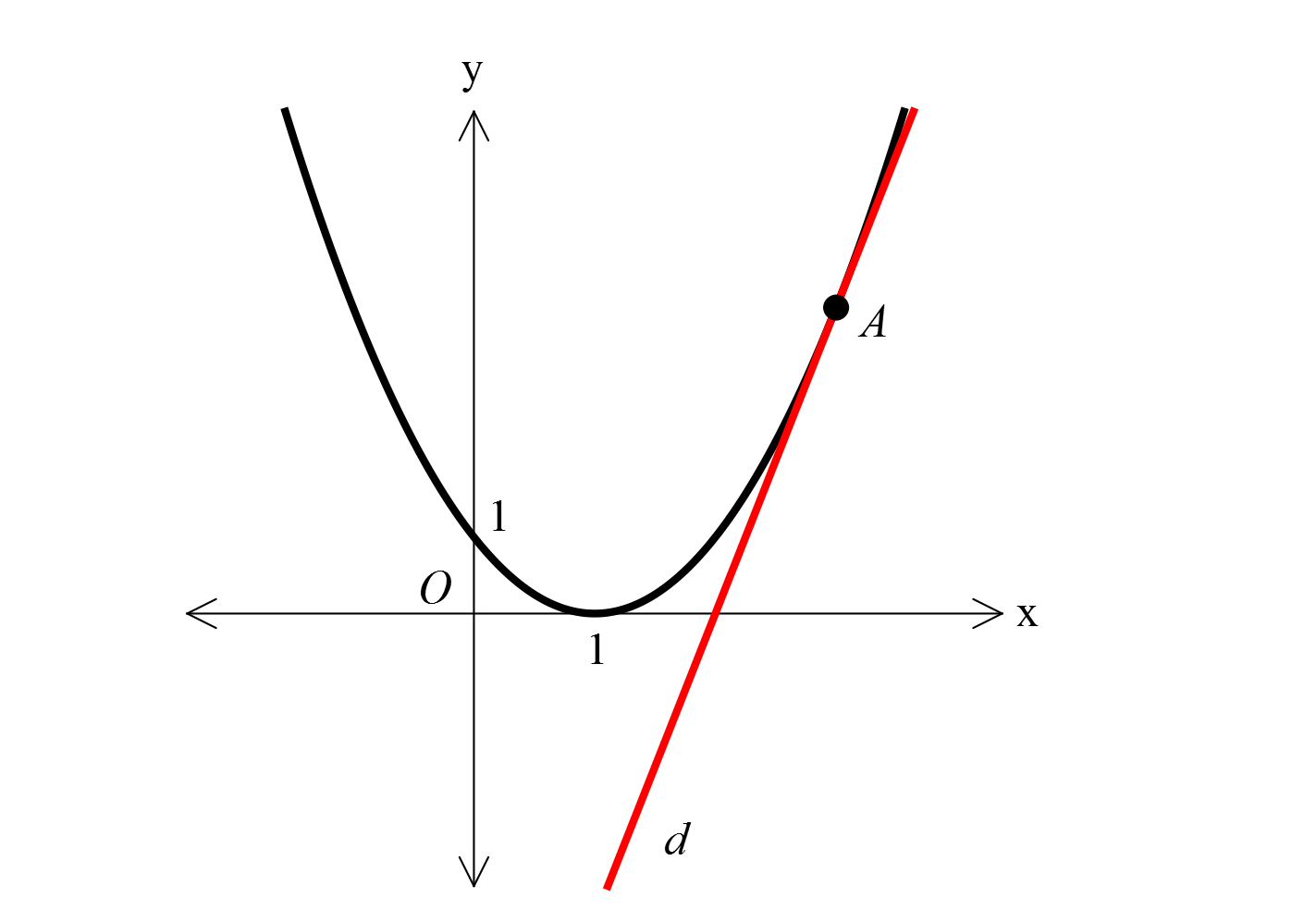
www.matematikkolay.net 2 Şekilde y mx 8 doğrusu y ax bx c parabolü – ne A noktasında teğettir. Buna göre, m kaçtır? A) 2 B) 1 C) 1 D) 2 E) 4 www.matematikkolay.net 2 Parabolün denklemini bulalım. Tepe noktası x ekseni üzerinde olduğundan k 0 dır. : y a x r Çözüm 2 0 1 2 1 0 1 2 şeklinde bir denkleme sahiptir. 1,0 noktası parabolü sağlar. y a(x r) r 1 olmalıdır. 0,1 noktası parabolü sağlar. y a(x r) 1 a dır. O halde parabol y x 1 dir. y mx 8 ile teğet ise, Çözü 2 2 2 2 2 m kümesi tek elemanlıdır. 0 dır. mx 8 x 1 mx 8 x 2x 1 0 x m 2 x 9 0 olmalıdır. m 2 4.1.9 0 m 2 36 m 2 6 m 4 buluruz. m’nin negatif bir değeri daha var. Ancak, y mx 8 doğrusu pozit if eğimli olduğundan bunu aramıyorduk. 78
2 2 2 y m x n parabolü, denklemi y x olan parabole teğet m olduğuna göre, oranının değeri ne o n labilir? 1 3 2 3 A) B) C) 1 D) E) 2 3 2 3 www.matematikkolay.net Teğet ise, iki denklemi birbirine eşitlediğimizde tek bir çözüm kümesi olmalıdır. Yani : 0 Çözüm 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 olmalıdır. m x n x m x 2xn n x m x 2xn n x 0 2x 2xn n m 0 olmalıdır. b 4ac 0 2n 4.2 n m 0 4n 8 n m 0 4n 8n 8m 0 8m 4n 2m n m 1 m 1 2 buluru n 2 n 2 2 z. 63
www.matematikkolay.net 2 Şekilde orjinden geçen d doğrusu A nokasından x y 1 parabolüne teğettir. Buna göre, A noktasının ap sisi kaçtır? www.matematikkolay.net 2 d doğrusu y mx olsun. x y 1 parabolü ile kesiştiği noktayı bulalım. iki denklemde de x’ : Çözüm 2 2 2 in eşitini birbirine eşitleyelim. İşlemler daha kolay olsun diye y y 1 m y my m 0 my y m olur. Parabol ile doğru bir noktada kesiştiklerinden bu denklemin çözüm kümesi tek elemanlı olmalıdır. 2 2 2 2 2 2 2 0 olmalıdır. 1 4.m.m 0 1 4m 0 1 1 4m m dir. 2 1 d doğrusu pozitif eğimli olduğundan m dir. 2 Kesiştikleri noktayı bulalım. y y 1 2y y 1 y 2y 1 0 m 2 2 2 y 1 0 y 1 dir. Şimdi apsisi bulalım. x y 1 x 1 1 2 buluruz. Cevap: 2 51

