Soru Sor sayfası kullanılarak Parabol konusu altında Parabolün denklemini yazma ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
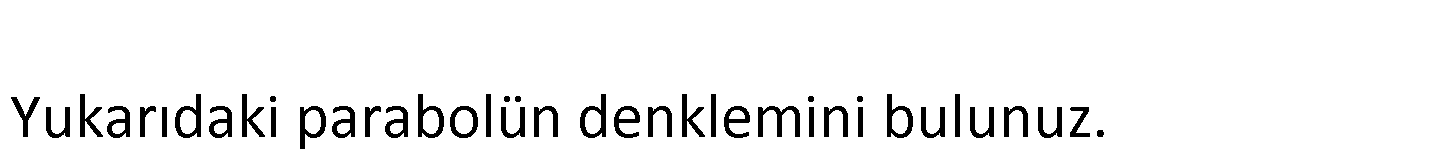

2.SORU
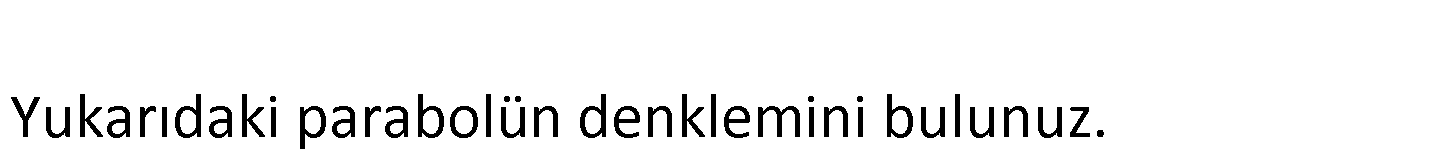

3.SORU
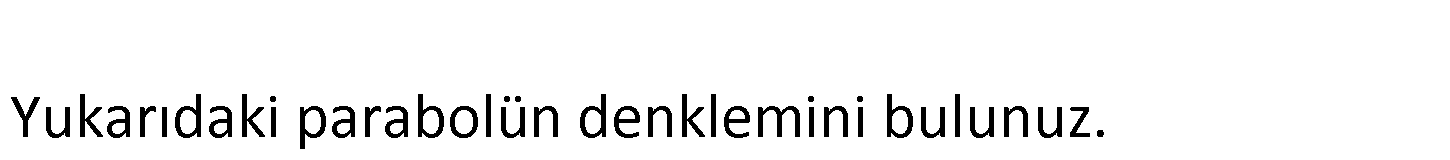

4.SORU
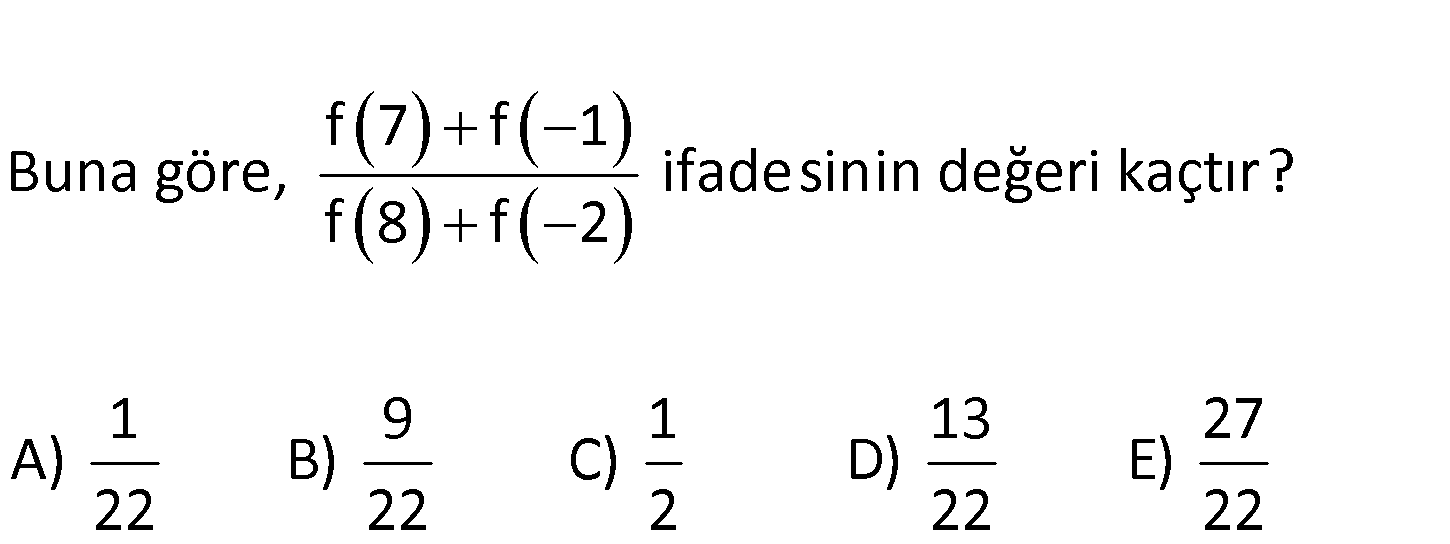

5.SORU


6.SORU


7.SORU


8.SORU


9.SORU


10.SORU


11.SORU


12.SORU

Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Çıkmış Sorular İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
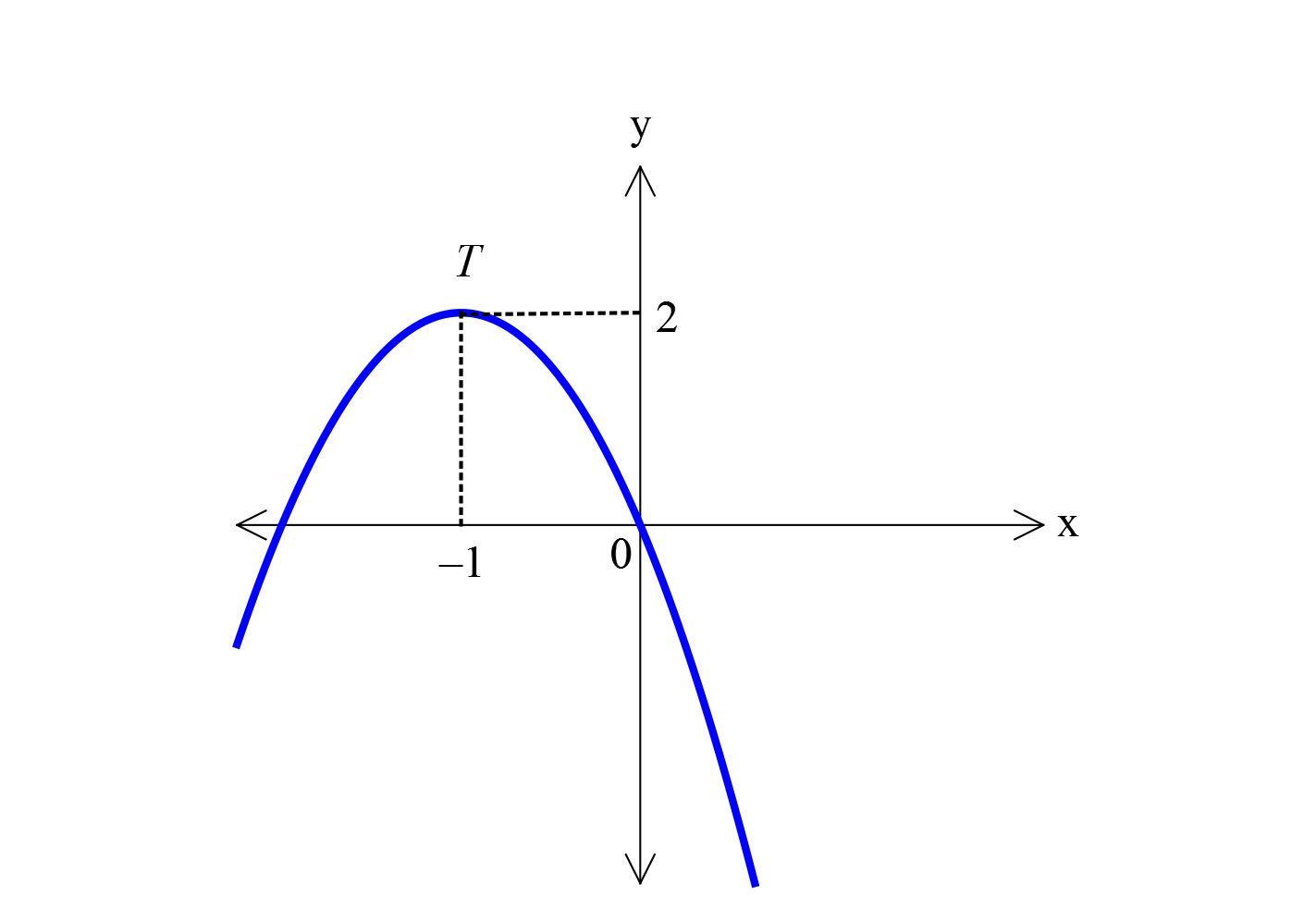
www.matematikkolay.net Yukarıdaki parabolün d enklemini bu lu nuz. 2 2 2 y a(x r) k Tepe noktasını T(r,k) ( 1,2) denkleme yazalım. y a(x ( 1)) 2 y a(x 1) 2 (0,0) n : o Çözüm 2 2 ktasından da parabol geçiyor. Bu noktayı da yazalım. 0 a(0 1) 2 0 a 2 a 2 dir. Buna göre parabol denklemi: y 2(x 1) 2 dir. 10
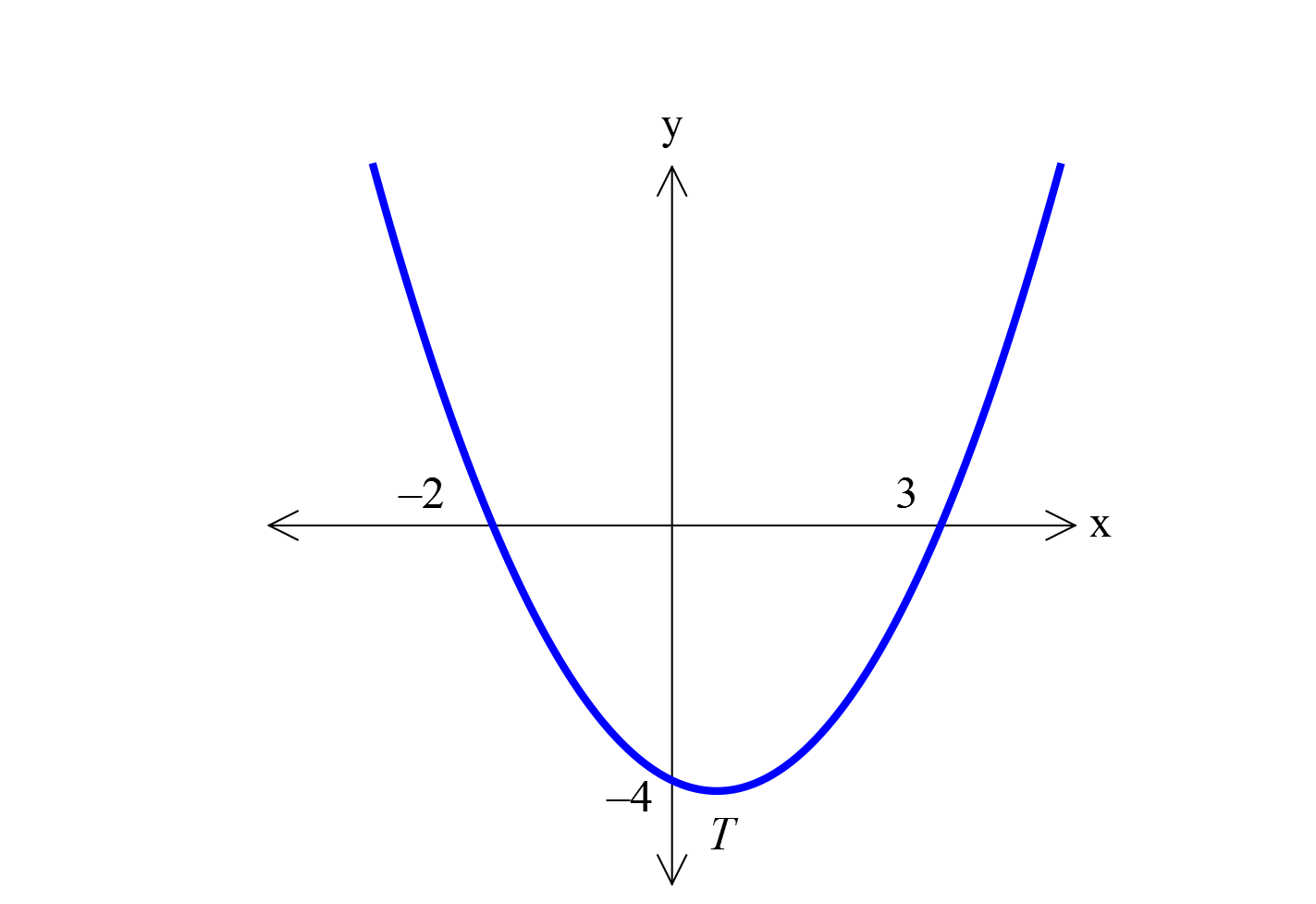
www.matematikkolay.net Yukarıdaki parabolün d enklemini bu lu nuz. 1 2 y a(x x )(x x ) x noktalarını yazalım. y a(x ( 2))(x 3) y a(x 2)(x 3) (0, 4) noktasından da a : p Çözüm rabol geçiyor. Bu noktayı da yazalım. 2 4 a(0 2)(0 3) 4 6a a dir. 3 Buna göre parabol denklemi: 2 y (x 2)(x 3) dir. 3 11
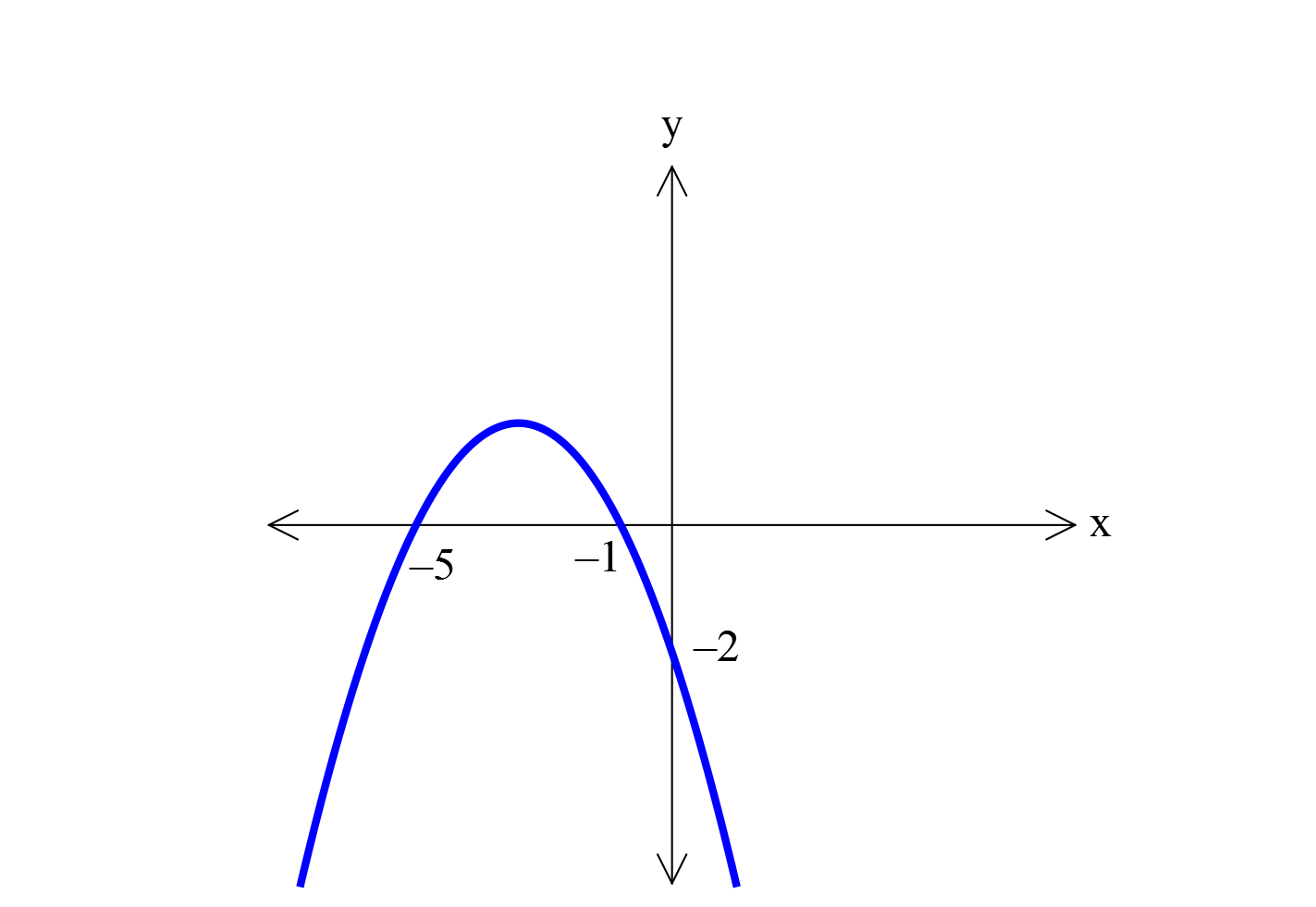
Yukarıdaki parabolün d enklemini bu lu nuz. www.matematikkolay.net x eksenini kesen noktalara göre parabolün denklemi: y a.(x ( 1)).(x ( 5)) y a.(x 1)(x 5) : Çözüm tir. (0, 2) noktasından da a’ yı bulalım. 2 a.(0 1)(0 5) 2 5a 2 a tir. 5 Buna göre; parabolun denklemini 2 y (x 1)(x 5) buluruz. 5 14
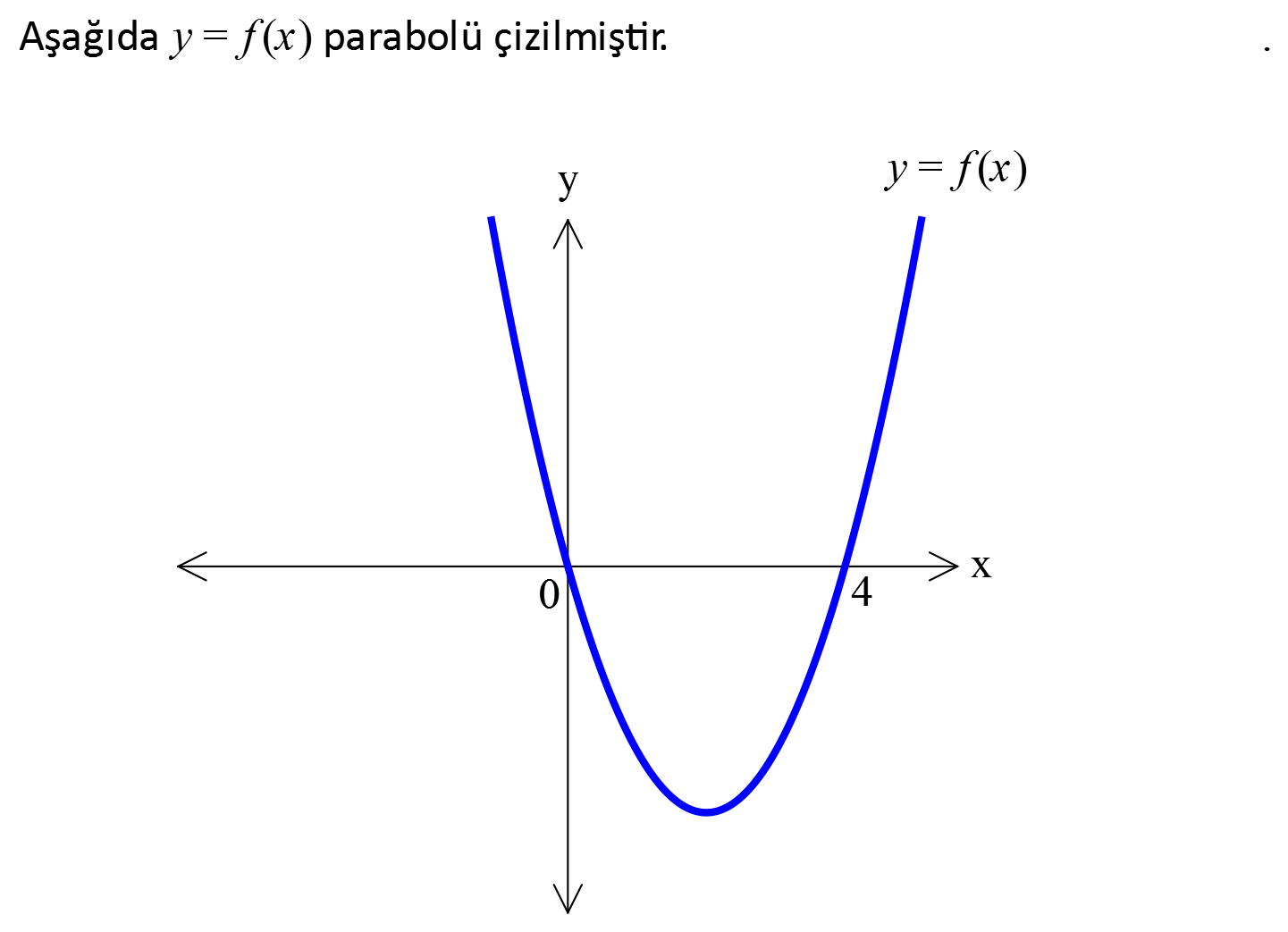
www.matematikkolay.net f 7 f 1 Buna göre, ifadesinin değeri kaçtır? f 8 f 2 1 9 1 13 27 A) B) C) D) E) 22 22 2 22 2 2 2 2 2 y a(x r) k r 2 olduğu soruda belli. y a(x 2) k dır. (0,0) noktası 0 a( 2) k k : Çözüm 2 2 2 4a dır. Buna göre; f(x) a(x 2) 4a dır. f(7) a.5 4a 21a f( 1) a.3 4a 5a f(8) 36a 4a 32a f( 2) 16a 4a 12a f(7) f( 1) 21a 5a 26a 13 buluruz. f(8) f( 2) 32a 12a 44a 22 www.matematikkolay.net 8
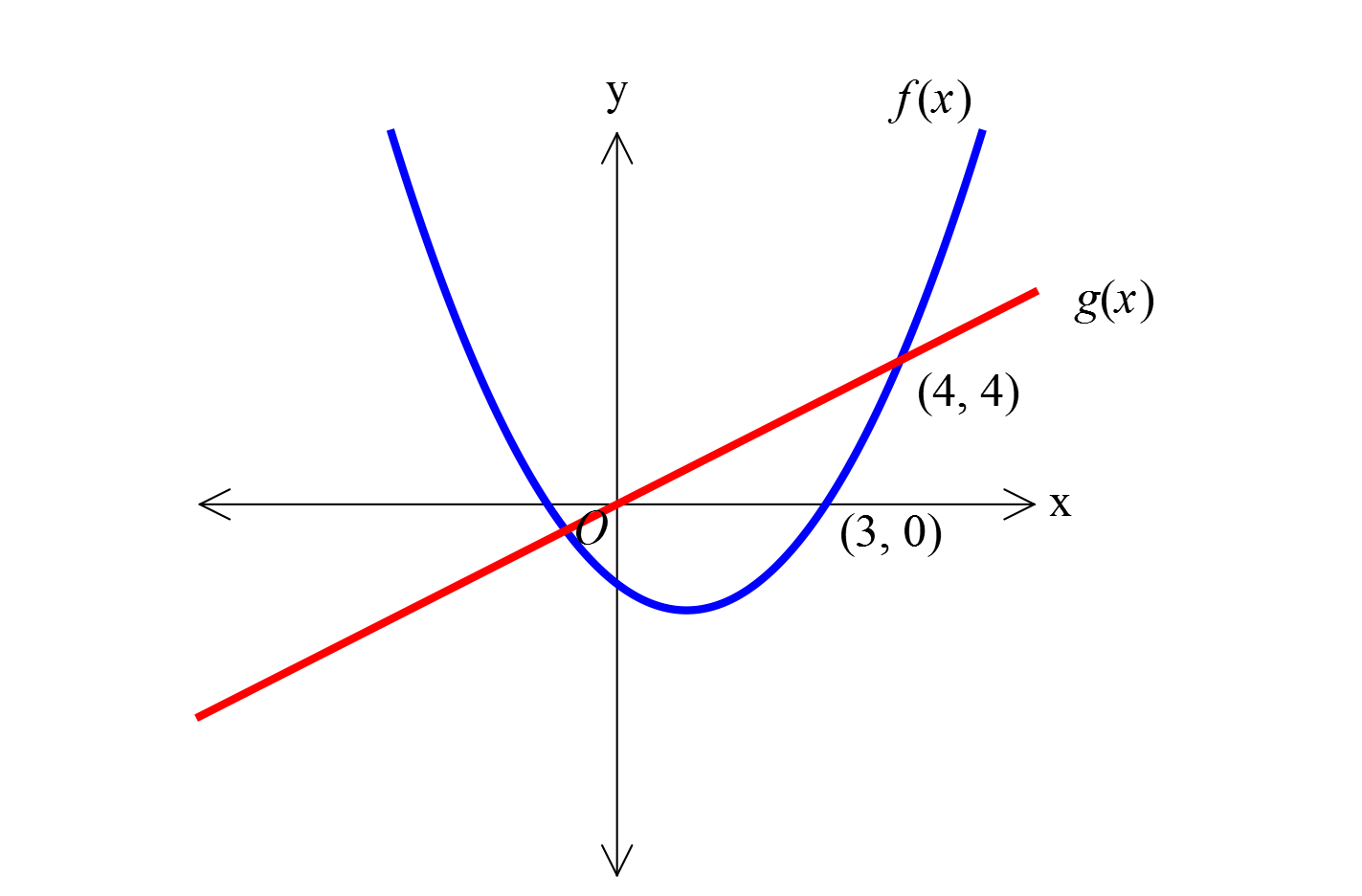
www.matematikkolay.net Şekilde verilen f x parabolü ile g x doğrusu 0, 0 ve 4, 4 noktalarında kesişmektedir. f o Buna göre, g 5 kaçtır? f o f 2 3 5 A) 1 B) C) 2 D) E) 3 2 2 2 Parabolun denklemini bulalım. 3 r değeri 0 ile 3’ün ortası 2 3 f(x) a(x ) k 2 (0,0) nok : Çözüm 2 2 2 3 9a tası için 0 a(0 ) k k 2 4 3 9a (4,4) noktası için 4 a(4 ) a 1 2 4 3 9 Buna göre f(x) (x ) dir. O halde; 2 4 (fog)(5) f(g(5)) f(5) 10 1 buluruz. (fof)(2) f(f(2)) f( 2) 10 20
www.matematikkolay.net 2 f x ax bx c parabolü x eksenini A 5, 0 ve B 1, 0 noktalarında kesmektedir. Buna göre; f 2 f 1 2 f 2 5 f 6 i fadesinin değeri kaçtır? A) 1 B) 2 C) 4 D) 5 E) 6 parabol a(x 5)(x 1) şeklinde bir denkleme sahiptir. Buna göre; f(2) f(1 2) f( 2 5) f( 6) a : .(2 Çözüm 5)(2 1) a.(1 2 5)(1 2 1) a.( 2 5 5)( 2 5 1) a.( 6 5)( 6 1) (2 5)(1) (6 2)( 2) ( 2)( 2 6) ( 1)( 7) 7 6 2 2 9 6 2 1 buluruz. 2 6 2 7 9 6 2 26
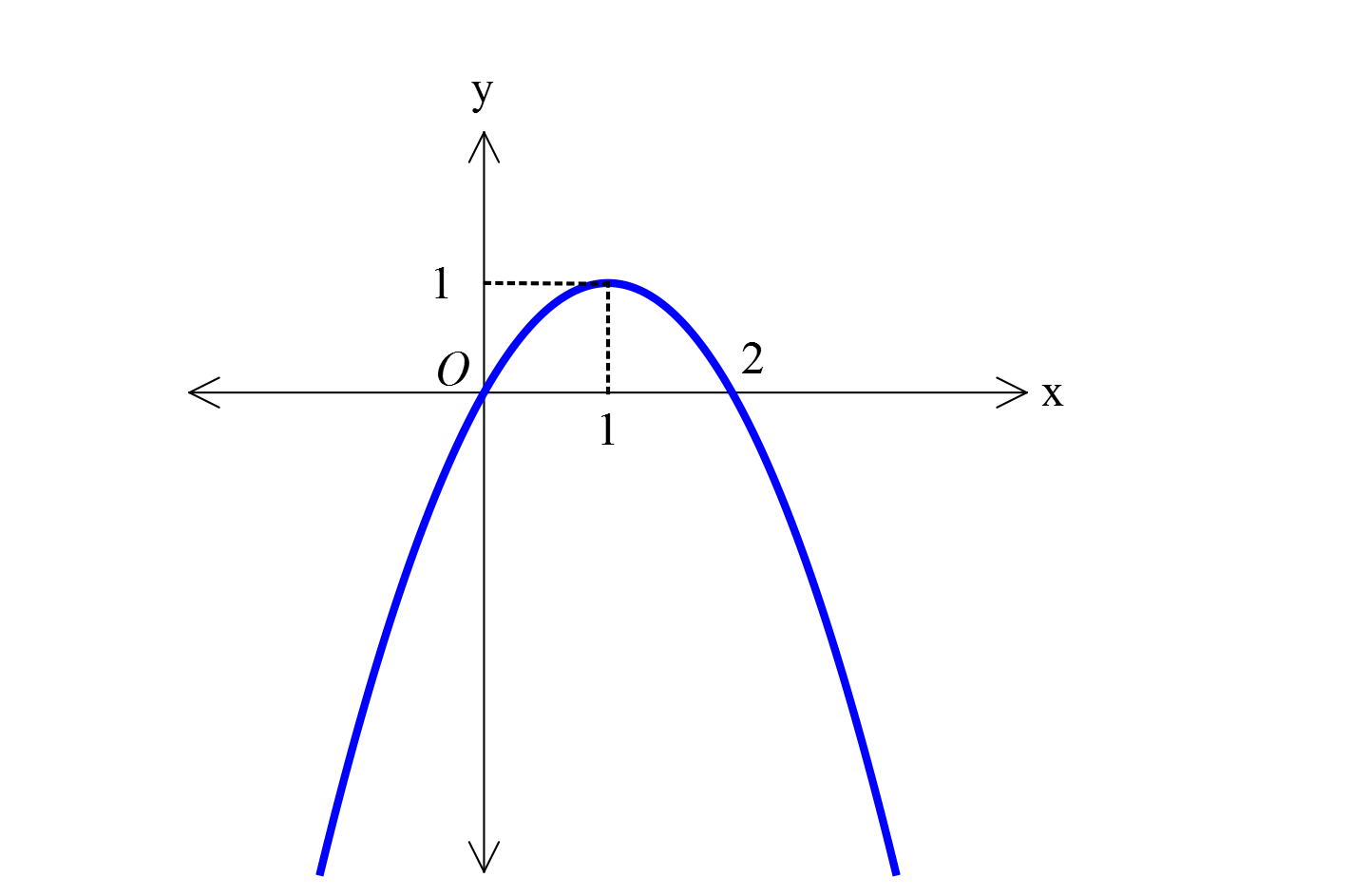
www.matematikkolay.net parabolünün denklemini bulunuz? 2 Tepe noktası (1, 1) noktasıdır. y a(x 1) 1 şeklinde bir denkleme sahiptir. (0,0) noktası : nd Çözüm 2 2 an da geçiyor. 0 a(0 1) 1 0 a 1 a 1 dir. y (x 1) 1 buluruz. 43
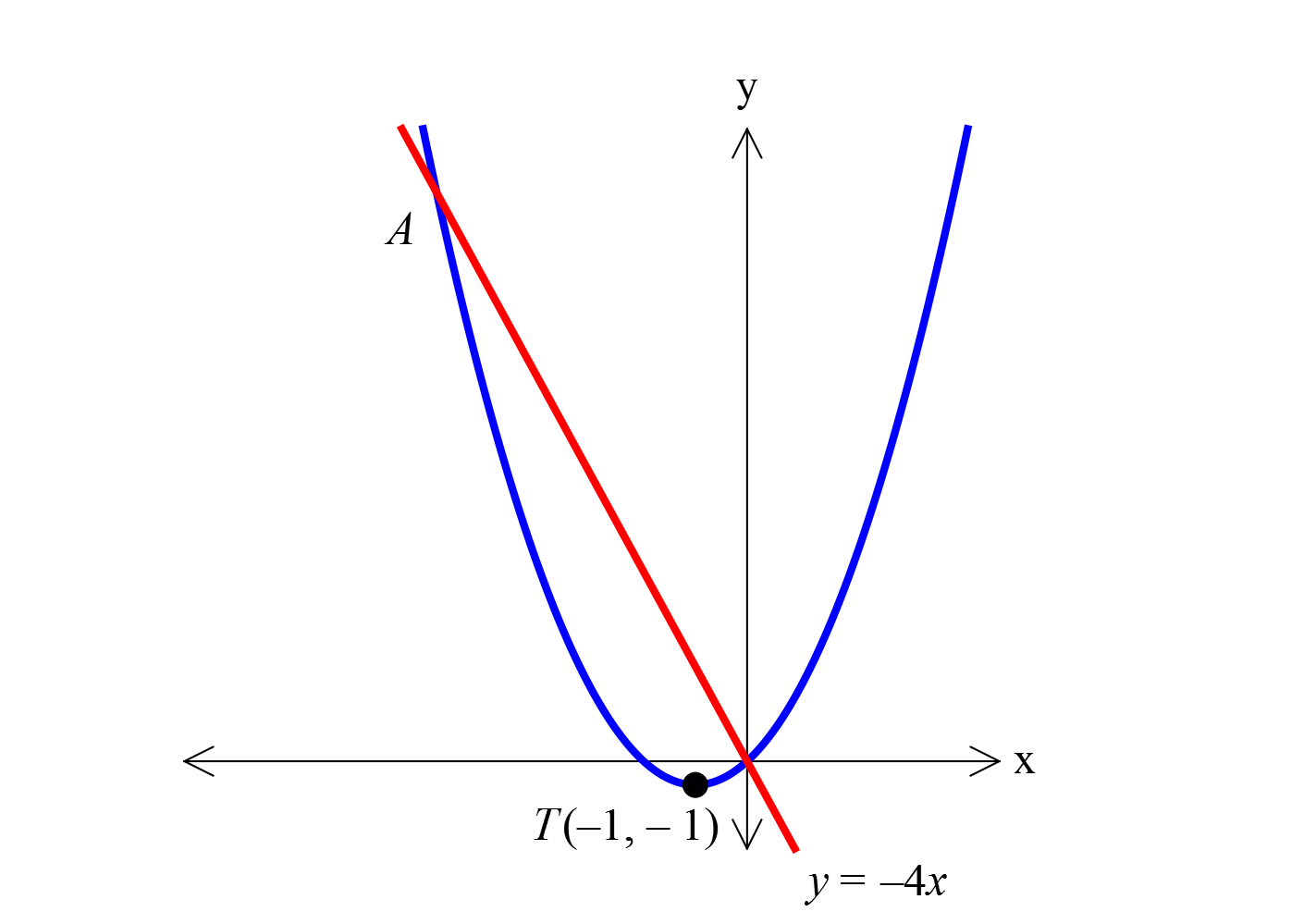
www.matematikkolay.net Parabolün tepe noktası T 1, 1 dir. Verilenlere göre, A noktasının ordinatı kaçtır? A) 8 B) 10 C) 14 D) 24 E) 26 www.matematikkolay.net 2 2 2 Tepe noktası bilinen doğru denklemi; y a x r k y a x 1 1 y a x 1 1 Parabol orjinden geçiy : or.Yan Çözüm 2 2 i 0,0 noktası denklemi sağlatır. 0 a 0 1 1 a 1 dir. y x 1 1 dir. Parabol y 4x doğrusuyla A noktasında kesişiyorsa A noktasının koordinatına x, 4x diyebiliriz. Bu nokta parabolün denklemince sağlatılır. 2 2 2 2 4x x 1 1 dir. 4x x 2x 1 1 4x x 2x x 6x 0 x x 6 0 x 0 ve x 6 dır. Negatif değeri almalıyız. A noktasının ordinatı y 4x 4. 6 24 bulunur. 50
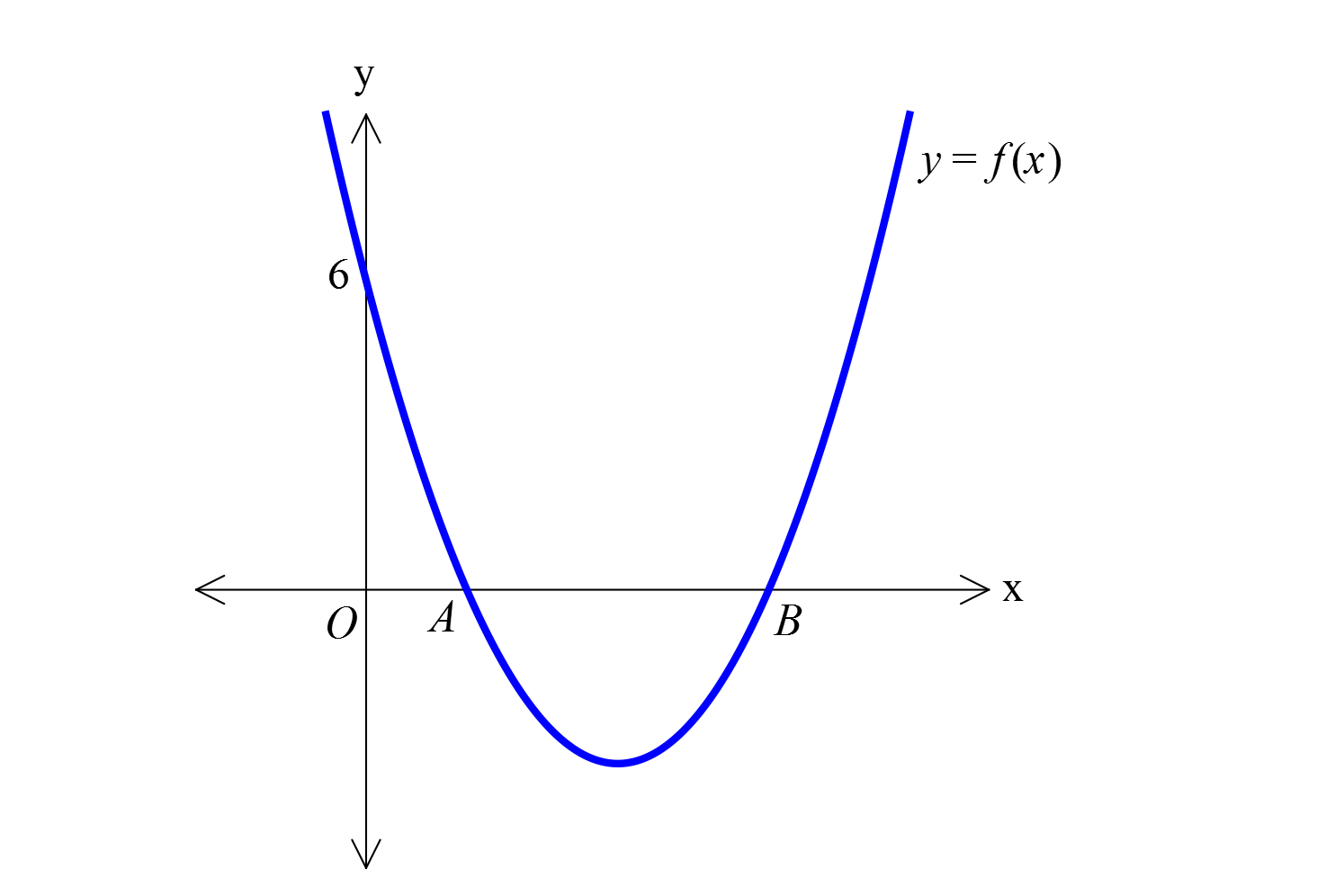
www.matematikkolay.net 2 Şekilde, denklemi y ax bx c olan parabol x eksenini A ve B noktalarında kesmekte ve 0, 6 noktasınd an geçmektedir. OA 1 olduğuna göre, AB 3 parabolünün tepe noktasının ordinatı kaçtır? 13 15 17 23 27 A) B) C) D) E) 5 7 4 9 8 OA 2k ve OB 6k şeklinde yazalım. A noktası 2k ‘da, B noktası 8k ‘da olur. y a( : x 2k) x 8k Çözüm 2 şeklinde bir polinomdur. 0, 6 noktasını yerine yazarsak; y a(0 2k) 0 8k 6 16k a 6 3 16 8 2 2 2 ak 3 ak dir. 8 2k 8k 10k Tepe noktasının apsisi r 5k dır. 2 2 r 5k’yı denklemde yazalım. y a(5k 2k) 5k 8k y 9ak 3 27 y 9 buluruz. 8 8 www.matematikkolay.net 59
2 f x ax bx c parabolü Ox eksenini 4, 0 ve 2, 0 noktalarından kesiyor. Parabolünün tepe noktası y 2x 5 doğrusu üzerin – de olduğuna göre, a b c toplamı kaçtır? A) 5 B) 4 C) 3 D) 2 E) 1 www.matematikkolay.net x eksenini 4 ve 2 noktasında kesen parabolun denklemi y a x 4 x 2 şeklindedir. : Parabolün Çözüm tepe noktasının apsisi, x eksenini kesen noktaların orta noktasıdır. 2 4 2 Yani; r 1 dir. 2 2 Tepe noktası, aynı zamanda y 2x 5 üzerinde ise bu doğru denkleminden tepe noktasının ordinatını bulalım. y 2. 1 5 2 5 3 tür. O halde tepe noktası T(1, 3) tür. Bu noktayı parabol denkleminde yazalım. y a x 4 x 2 3 a 1 4 1 2 3 a 3 2 2 1 .3 a tür. 3 1 1 1 2 8 y x 4 x 2 x 2x 8 x x 3 3 3 3 3 1 2 8 9 a b c 3 buluruz. 3 3 3 3 64
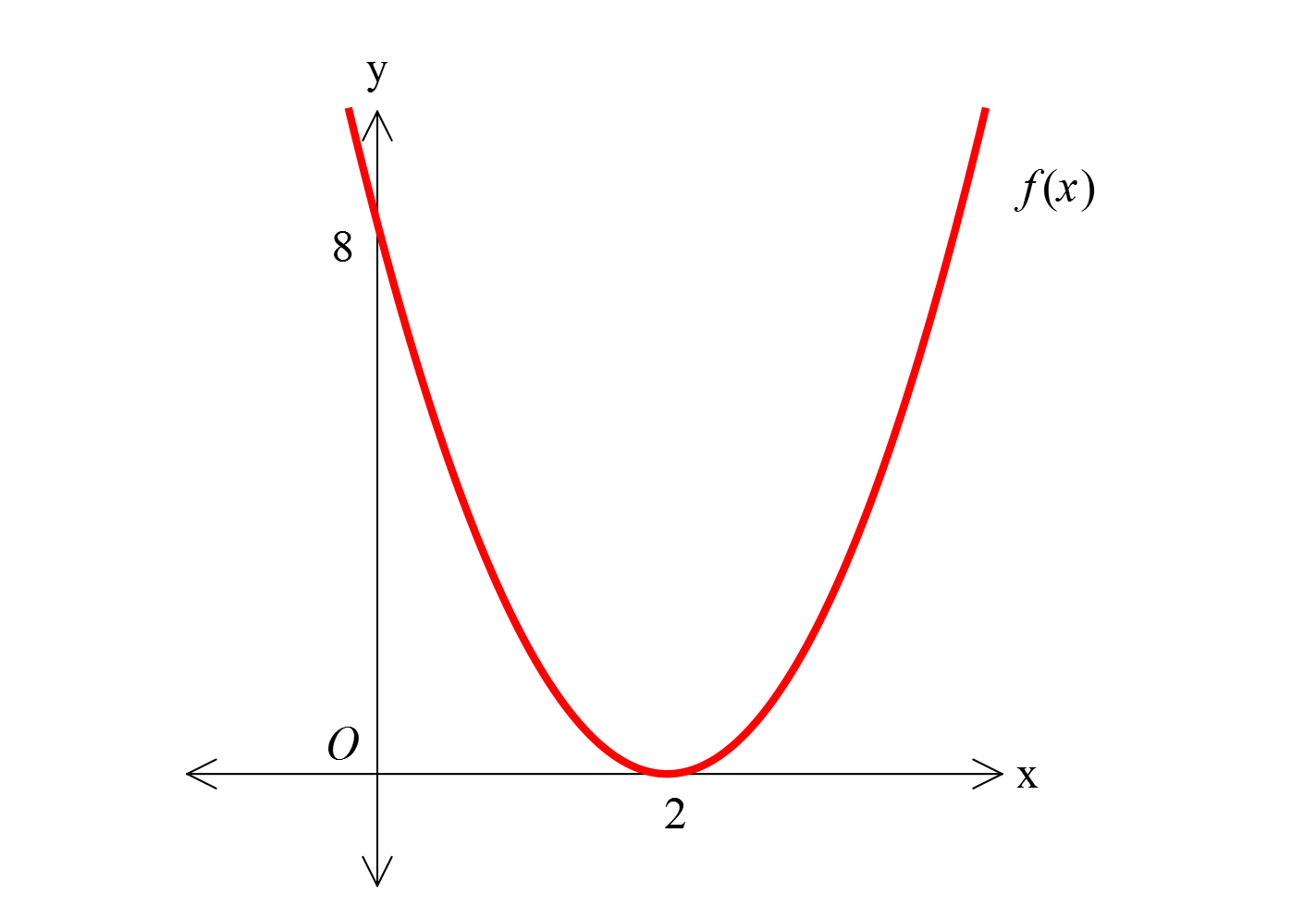
www.matematikkolay.net Şekilde y f x parabolünün grafiği verilmiştir. Buna göre, f 3 f 2 toplamı kaçtır? A) 12 B) 14 C) 16 D) 34 E) 40 2 x eksenine teğet parabol denklemi f(x) a x r şeklindedir. x 2 değeri için fonksiyon 0 dır. : O Çözüm 2 2 2 0 2 2 2 halde r 2 olmalıdır. f(x) a x 2 olur. x 0 için fonksiyon 8 ise, f(0) a x 2 8 a 2 8 a 2 dir. f(x) 2 x 2 olur. f 3 2 3 2 2 f 2 2 2 2 2.16 32 dir. Toplamları 2 32 34 buluruz. 69
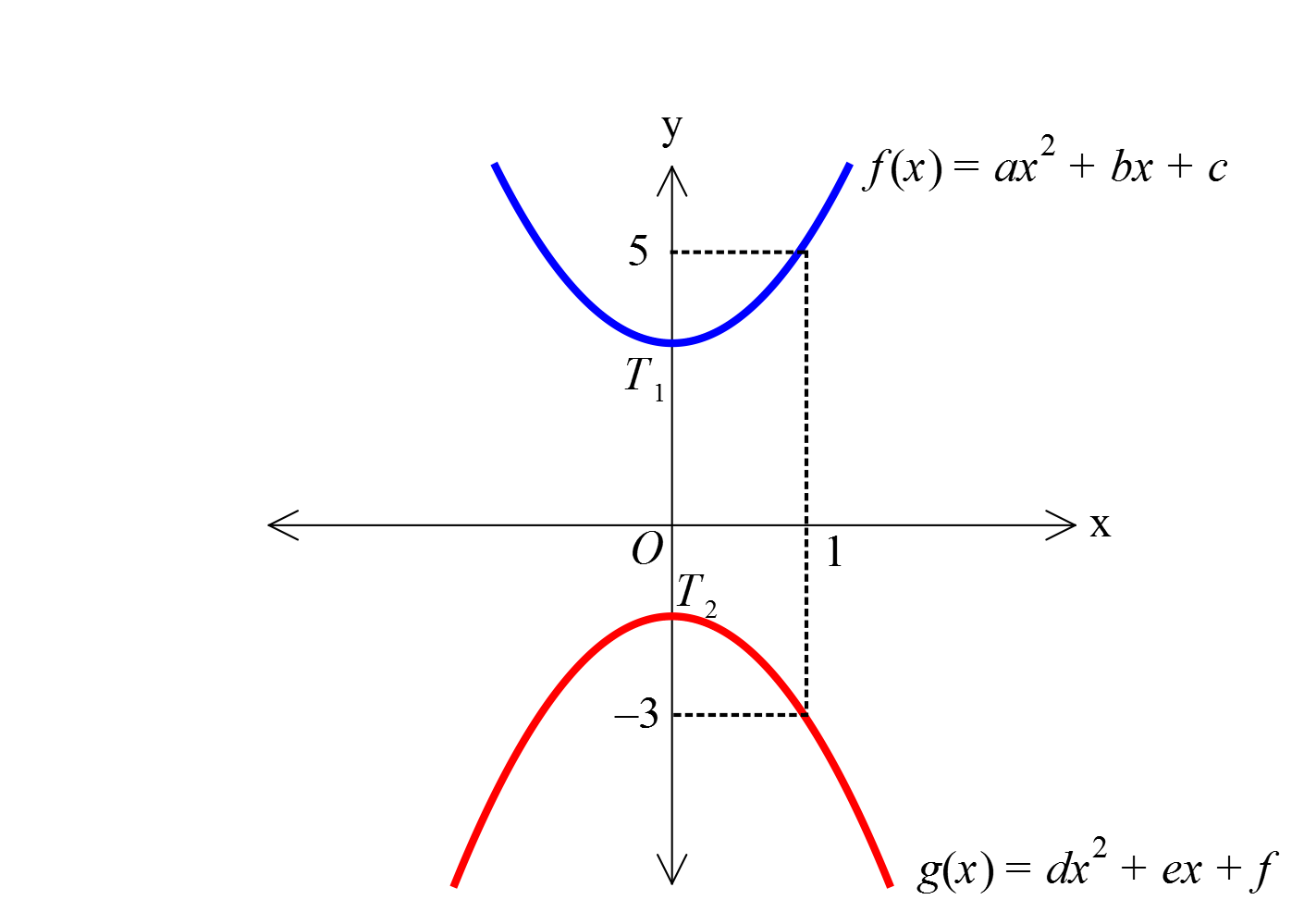
www.matematikkolay.net Şekilde grafiği verilen f x ve g x için a c d f kaçtır? A) 5 B) 4 C) 3 D) 2 E) 1 1 1 1 2 2 2 2 T (0,k ) r 0 b 0 b 0 dır. 2a T (0,k ) r 0 e 0 e 0 dır. 2d f(x) ax c f(1) 5 a c 5 tir. g( ) : x Çözüm 2 dx f g(1) 3 d f 3 tür. a c d f 5 ( 3) 2 bulunur. 18

