Soru Sor sayfası kullanılarak Rasyonel Sayıların Sıralanması konusu altında Verilen aralıktaki kesri bulma ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
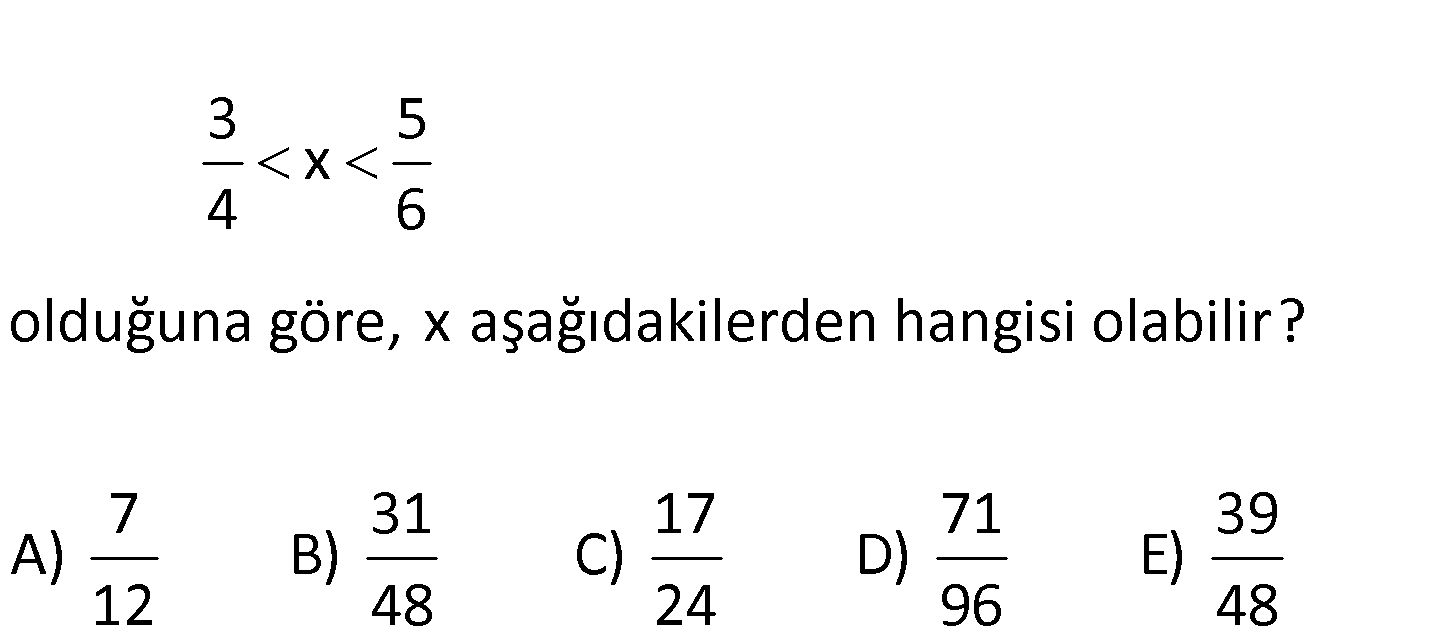

2.SORU
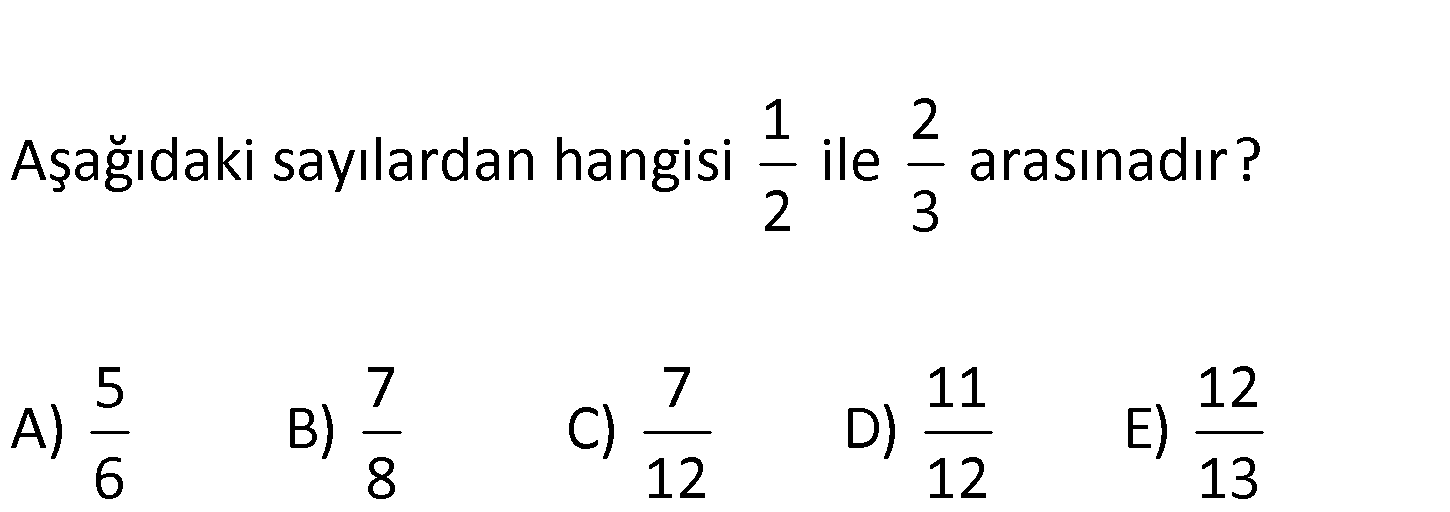

3.SORU
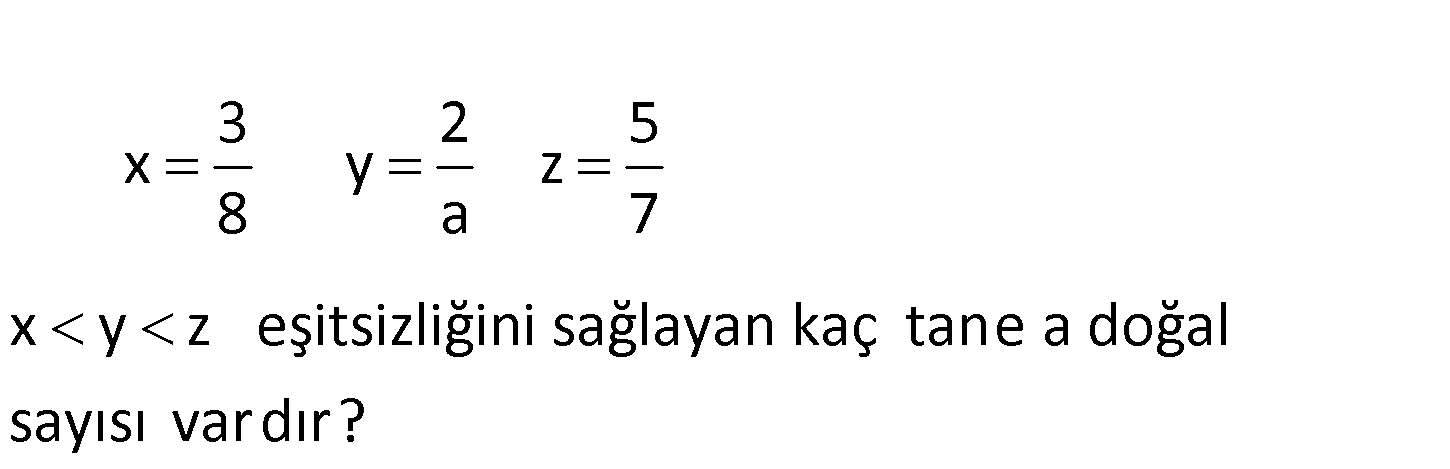

4.SORU


5.SORU


Diğer Soru Tipleri için Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
2 kesri bileşik kesirdir. x 5 Buna göre, x’in doğal sayı değerlerinin toplamı kaçtır? A) 28 B) 25 C) 23 D) 20 E) 18 www.matematikkolay.net 2 1 için baktığımızda paydanın negatif x 5 veya pozitif olması çok önemli. Payda pozi : tif ike Çözüm n inceleyeceğiz. x 5 için 2 6 ve 7 1 2 x 5 7 x x 5 Payda negatif iken inceleyeceğiz. x 5 için 2 3 ve 4 1 2 x 5 x 3 x 5 Toplarsak; 3 4 6 7 20 buluruz. 5
x 5 x Z ve ifadesi basit kesir olduğuna göre, 11 x kaç farklı değer alabilir? A) 16 B) 15 C) 14 D) 13 E) 12 www.matematikkolay.net Basit kesir ise, pay kısmı mutlak değerce paydadan küçük olmalıdır. Yani; 11 x 5 11 di : r. Çözüm Her tarafa 5 ekleyelim. 6 x 16 olur. x pozitif bir tam sayı ise; 1’den 15’e kadar tüm tam sayı değerlerini alır. Cevap: 15 15
Pay ve paydası sırasıyla 30 ve 40 tan küçük pozitif 30 tam sayı olan kesrine denk kaç kesir vardı 40 r? A) 9 B) 10 C) 11 D) 12 E) 13 : 30 3.10 40 Çözüm 04.Eki 3 tür. 4 30 ‘ tan küçük ve bu kesre denk kesirler; 40 3 6 9 27 … 4 8 12 36 3.1 3.2 3.3 3.9 … 9 tane 4.1 4.2 4.3 4.9 9 denk kesir bulunur. 2
12 x 2 kesri bileşik kesir olduğuna göre, x ‘in alabileceği kaç farklı tamsayı değeri var dır? A) 25 B) 24 C) 23 D) 22 E) 21 www.matematikkolay.net a a Not : bileşik kesir ise 1 olmalıdır. b b 12 1 Takla attıralım. x 2 x 2 1 olur. 12 x : Çözüm 2 12 12 x 2 12 14 x 10 aralığını buluruz. 10 14 Terim sayısı 1 25 tir. 1 Ancak x 2 değeri paydayı 0 yaptığı için bunu kullanamayız. Kesir tanımsız olur. 25 1 24 farklı x değeri var dır. 6
15 x 3 kesrinin bileşik kesir olabilmesi için x in alabilceği tam sayı değerlerinin toplamı kaçt ır? A) 105 B) 96 C) 90 D) 87 E) 84 www.matematikkolay.net 15 x 3 15 olmalıdır. 18 x 12 18 den 12’ye kadar tüm tam sayı değerlerini alab : ilir. Toplamı Çözüm Terim Sayısı.Or tanca Terim 12 ( 18) 12 ( 18) 1 1 2 6 31 2 31 ( 3) 93 buluruz. Ancak x 3 için payda 0 değerini alır. Bu da kesri tanımsız yapar. O yüzden 3 değerini çıkaralım. 93 ( 3) 90 buluruz. 14

