Soru Sor sayfası kullanılarak Diziler konusu altında Ardışık sayıların kareleri toplamı ile oluşturulan diziler ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU


2.SORU



3.SORU

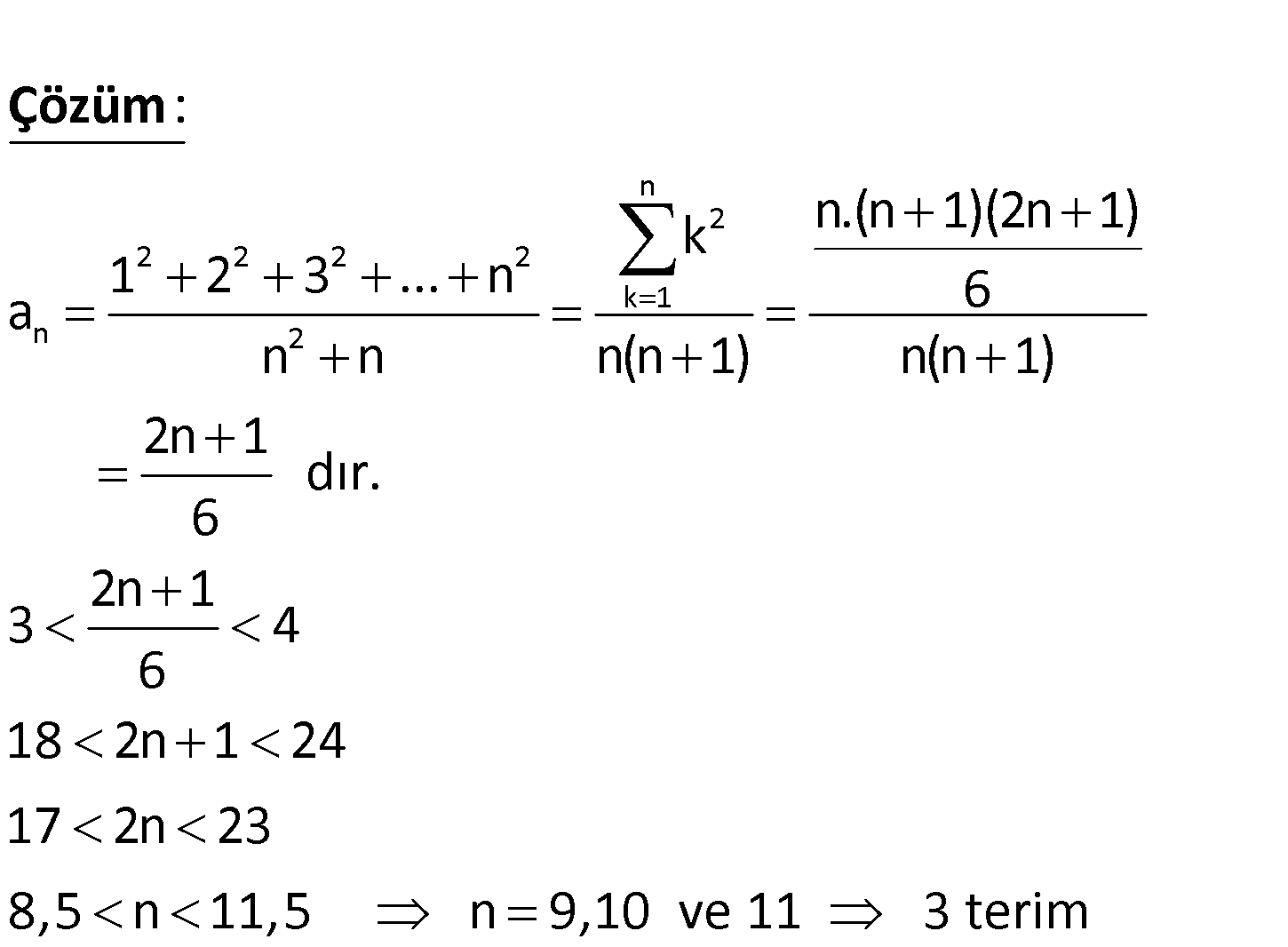
Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
2 n 2 2 2 n n a m.n m.n 2n 1 dizisi ile genel terimi b 6 12 … 6n olan b dizisi eşit diziler olduğuna göre, m kaçtır? A) 1 B) 2 C) 4 D) 6 E) 8 www.matematikkolay.net 2 n n 2 k 1 n a (m.n m.n)(2n 1) m.n.(n 1)(2n 1) n.(n 1)(2n 1) Not : k dır. 6 a m.n.(n 1)(2n 1 m : ) .6 Çözüm n 2 k 1 n n n 2 2 2 2 k 1 n 2 2 2 2 2 k 1 2 k şeklinde yazabi – liriz. a b ise; 6m k 6 12 … 6n 6m k 6 (1 2 3 … n ) 6m 6 m 6 buluruz. 18
Kutulardan oluşan şeklin birinci sırasına 1, ikinci sırasına 2, üçüncü sırasına 3 ve n inci sırasına n tane olmak üzere, ardışık tek sayılar her sıraya 1 den başlayıp sırasıyla yazılarak bir dizi oluşturulu – yor. Oluşturulan dizinin terimleri sırasıyla satır – lardaki ardışık sayılar toplanarak elde ediliyor. Bu dizinin ilk 20 terimin toplamı kaçtır? A) 1440 B) 1680 C) 2520 D) 2650 E) 2870 www.matematikkolay.net n 2 2 k 1 n. satırın toplamı n(n 1) 2k 1 2 n n n n n ile bulunur. 2 Yani bu dizinin her bir terim : Çözüm 2 20 2 n 1 i n ile bulunur. İlk 20 terimin toplamı ise; 20.21.41 n 2870 buluruz. 6 20
2 2 2 2 n 2 n 1 2 3 … n a dizisi veriliyor. n n Buna göre, a dizisinin kaç terimi 3 ile 4 a rasında – dır? A) 2 B) 3 C) 4 D) 5 E) 7 www.matematikkolay.net n 2 2 2 2 2 k 1 n 2 k n.(n 1)(2n 1) 1 2 3 … n 6 a n n n(n 1) n(n 1) 2n 1 dır. 6 2n 1 3 4 6 18 2n 1 : Çözüm 24 17 2n 23 8,5 n 11,5 n 9,10 ve 11 3 terim 8

