Soru Sor sayfası kullanılarak Diziler konusu altında Aritmetik dizinin genel terimini bulma ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU


2.SORU


3.SORU
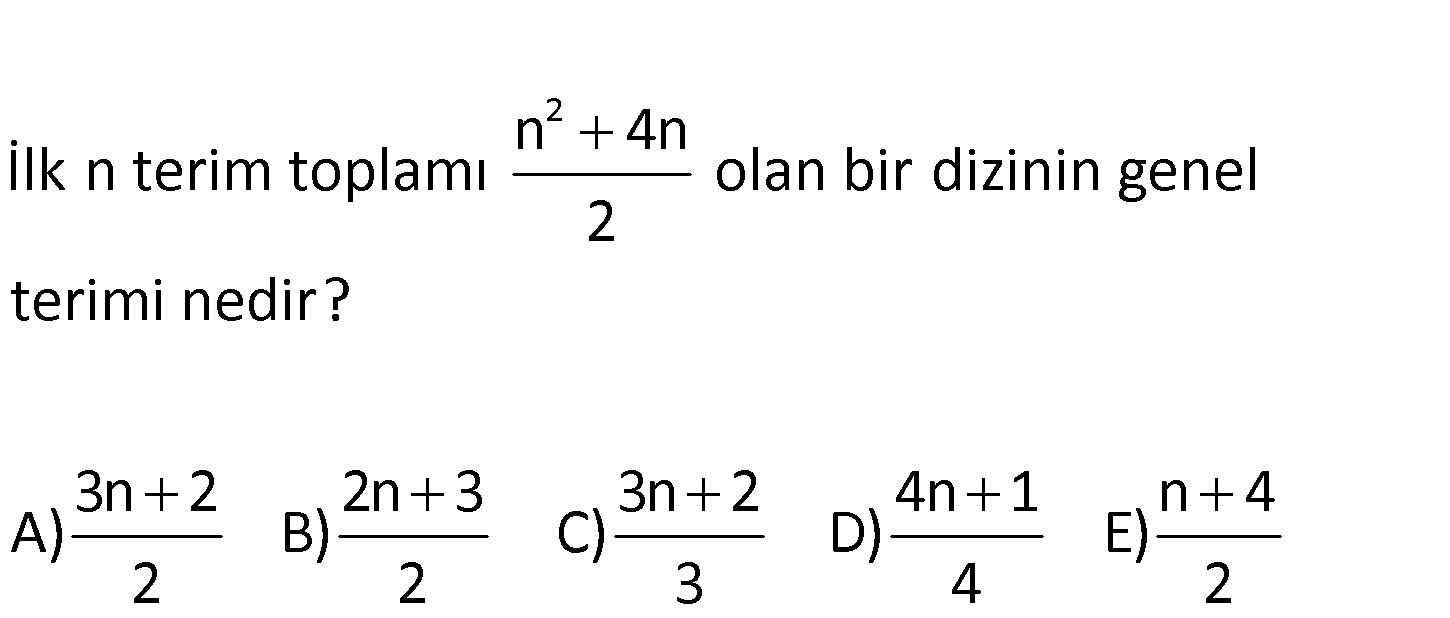

4.SORU


5.SORU


6.SORU


Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
n n 1 n 1 olmak üzere, a 4 a ve ilk 15 terim toplamı 510 olan aritme – tik dizinin genel terimi aşağıda kilerden hangisidir? A) 4n-2 B) 4n2 C) 4n- 4 D) 2n4 E) 2n-2 www.matematikkolay.net n n 1 15 n 1 15 15 n 1 n 1 a a 4 tür. Artış miktarı 4 olan 15 terimin toplam 4 : ı; 4n b 510 4 n b 510 Çözüm 15.(15 1) 15b 510 2 4 2 15.16 2 15b 510 480 15b 510 15b 30 b 2 dir. Buna göre, genel terim 4n 2 buluruz. 14
x inci terimi y, y inci terimi x olan aritmetik dizinin genel terimi aşağıdakilerden hangisidir? A) x y n B) x y n C) y x n D) x y n E) x y n www.matematikkolay.net an b şeklinde genel terim olsun. x inci terim ax b y y inci terim ay b x İki tarafın d : Çözüm a farkını alalım. ax ay y x a(x y) y x a 1 dir. x inci terim x b y b x y dir. Buna göre genel terim; an b n x y x y n buluruz. 15
2 n 4n İlk n terim toplamı olan bir dizinin genel 2 terimi nedir? 3n 2 2n 3 3n 2 4n 1 n 4 A) B) C) D) E) 2 2 3 4 2 2 1 1 2 İlk 1 terim toplamı, 1.terimi verir. n 4n 1 4 5 a dir. 2 2 2 İlk 2 terim toplamı, a a ‘ yi : Çözüm 2 2 1 2 2 2 n 1 n n n n verir. n 4n 2 8 4 8 a a 6 dır. 2 2 2 5 7 a 6 a dir. 2 2 7 5 2 Artış miktarı 1 dir. 2 2 2 Genel terim: a a (n 1)d 5 5 a (n 1).1 a n 1 2 2 3 2n 3 a n a buluruz. 2 2 32
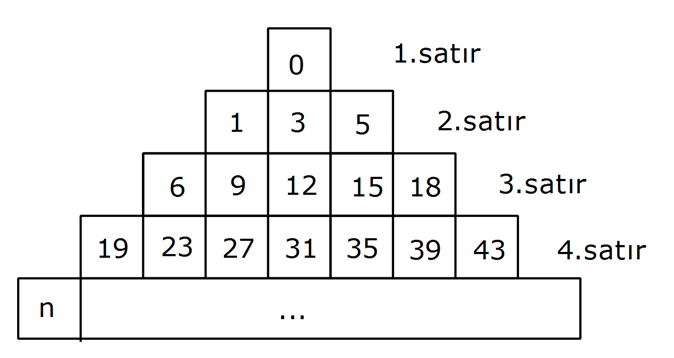
www.matematikkolay.net Yukarıda gösterilen şekilde sayılar belirli bir kurala göre dizilmiştir. Buna göre, n. satırdaki en 3 2 2 büyük sayı ile en küçük sayı arasındaki farkın pozitif değeri kaçtır? A) n 2 B) n C) n n D) 2n 2n E) n 2n www.matematikkolay.net 1.satırda en büyük sayı ile en küçük sayı arasındaki fark 0 dır. 2.satırda 5 1 4 3.satırda 18 : Çözüm n n 1 n n 1 6 12 4.satırda 43 19 24 tür. 4’ün katları şeklinde bir artış görüyoruz. ve bir önceki sayı ile bu artış toplanıyor. Buna göre; Bu farkı, (k 1).4 şeklinde yazabiliriz. 4 (k 1) 4 2 n(n 1) 2 2 2 4n 2n 2n 4n 2n 2n buluruz. 50
n Genel terimi a 1 3 5 … 2n 1 olan dizinin kaçıncı terimi 36 dır? A) 4 B) 5 C) 6 D) 7 E) 8 www.matematikkolay.net n Dizinin genel terimini bulalım. a 1 3 5 … 2n 1 Son terim 2n 1 olunca tek sayıların toplamı : Çözüm 2 n n n 2 n 2 n ile bulunur. Genel formülden de bunu bulabiliriz. Son T. İlk T. Son T. – İlk T. a 1 2 Artış Miktarı 2n 1 1 2n 1 1 a 1 2 2 a n n a n dir. 36 n ise n 6 buluruz. Cevap: 6 77
0, 3, 6, 9, … 1 2009, 2005, 2001, … 2 Yukarıdaki ifadeler iki farklı sayı dizisinin ardışık sayı terimleridir. Bu sayı dizisinin baş tan n. terimleri eşit olduğuna göre, n kaçtır? A) 284 B) 285 C) 286 D) 287 E) 288 www.matematikkolay.net 0,3,6,9,… dizisi 0’dan başlayan ve 3’er 3’er ar tan 1 dizidir. Bu diziyi 3(n 1) olar f : ak i Çözüm ade edebiliriz. 2009,2005,2001,… dizisi 2009’dan başlayan ve 4’er 4’er azalan dizidir. Bu diziyi 2009 4(n 1) olarak ifade edebiliriz. Bunların eşit olduğu yeri bulalım. 3(n 1) 2009 4(n 1) 7(n 1) 2009 n 1 287 n 288 buluruz.

