Soru Sor sayfası kullanılarak Sayıların Çözümlenmesi konusu altında Basamakları çözümleyerek şartlara uygun sayıları bulma ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU

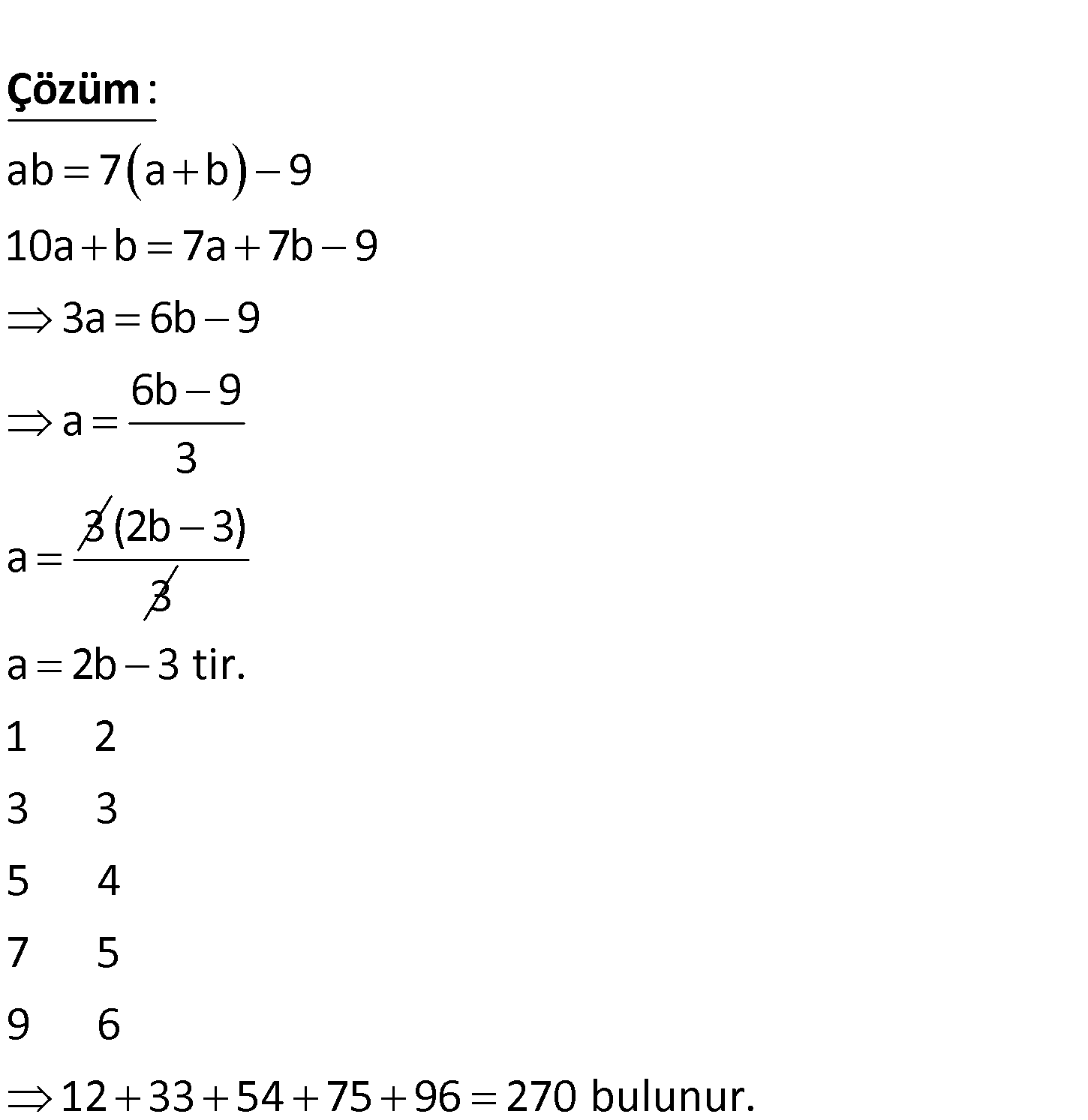
2.SORU


3.SORU


4.SORU


5.SORU

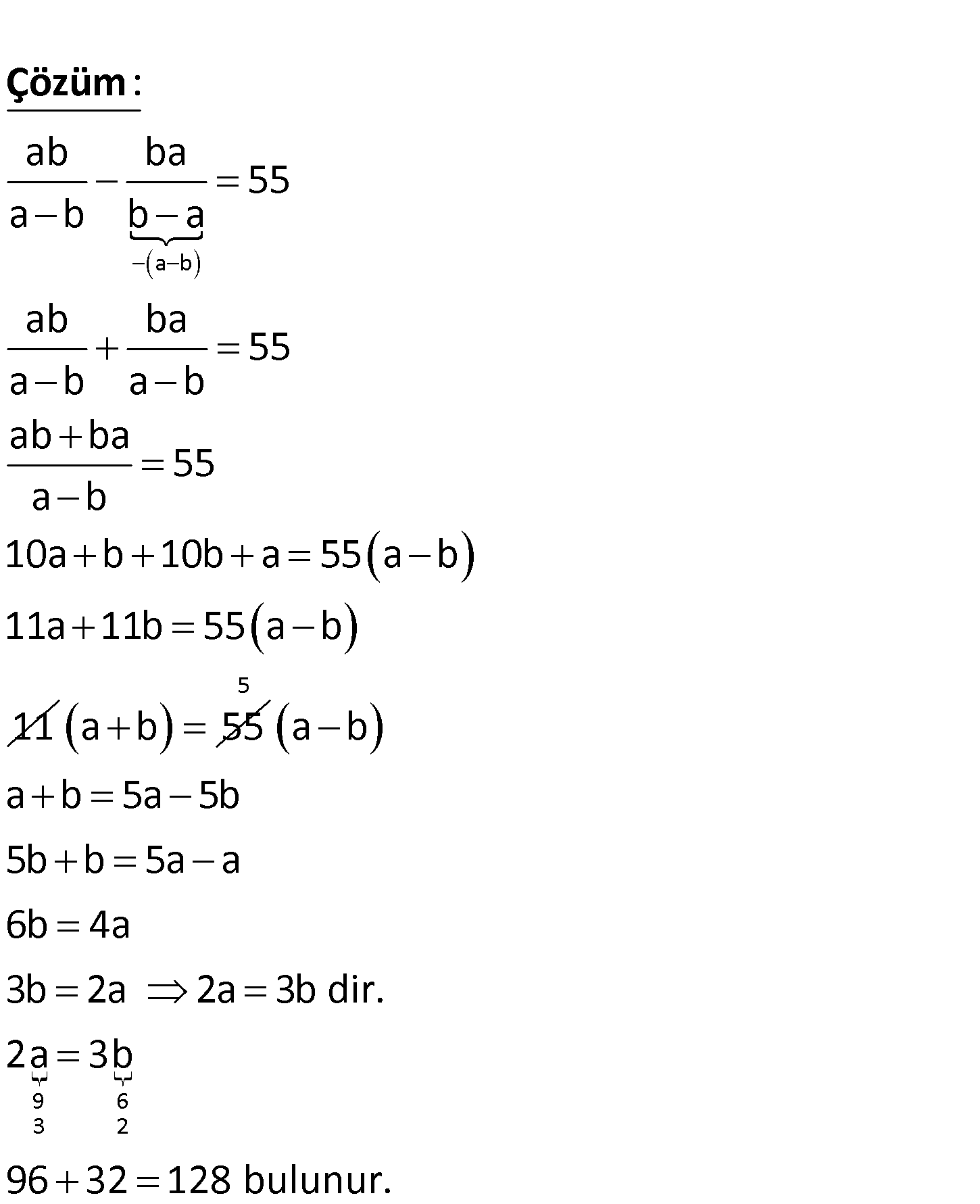
6.SORU


7.SORU


8.SORU

9.SORU


10.SORU


Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
ab iki basamaklı sayısı rakamları toplamının 7 katından 9 eksiktir. Bu koşula uyan iki basamaklı doğal sayıların toplamı kaçtır? A) 174 B) 195 C) 237 D) 270 E) 396 ab 7 a b 9 10a b 7a 7b 9 3a 6b 9 6b 9 a 3 3 a : Çözüm (2b 3) 3 a 2b 3 tir. 1 2 3 3 5 4 7 5 9 6 12 33 54 75 96 270 bulunur. 26
ab iki basamaklı sayısı ile ba iki basamaklı sayısının farkı daima bir doğal sayının küpü olduğuna göre, bu şartı sağlayan kaç tane ab sayısı vardır? A) 4 B) 5 C) 6 D) 12 E) 15 www.matematikkolay.net 3 3 3 3 3 2 3 0 veya 3 olmalı. ab ba x 10a b (10b a) x 10a b 10b a x 9a 9b x 9.(a : b) x 3 .(a b) x a b Çözüm 9 6 8 5 7 4 6 3 5 2 4 1 0 a b a ve b 1’den 9’a kadar tüm rakamları alabilir. 9 adet buradan gelir. a b 3 6 adet ab de burdan gelir. Toplam 15 ab ikilisi bulunur. 34
u a, b, c birer rakam ve abc üç basamaklı ab, ac iki basamaklı sayılardır. ab .c ac .b 10 koşul nu sağlayan kaç tane abc sayısı var dır? A) 10 B) 9 C) 8 D) 7 E) 6 www.matematikkolay.net 1 2 3 … 9 ab .c ac .b 10 10a b .c 10a c .b 10 10ac bc 10ab bc 10 10ac 10ab 10 ac ab 1 a(c b) 1 a 1 dir. : c Çözüm 0 1 2 … 8 b 1 dir. 9 farklı b – c ikilisi var dır. a 1 dir. Buna uygun 9 tane abc sayısı var dır. 37
r Üç basamaklı bir sayının birler basamağı ile yüzler basamağı yer değiştirdiğinden sayı 495 azalıyo . Bu koşulu sağlayan kaç tane üç basamaklı sayı yazılabilir? A) 32 B) 40 C) 45 D) 50 E) 56 www.matematikkolay.net Üç basamaklı sayı abc olsun. Bu sayının birler basamağı ile yüzler basamağı yer değiştirirs Çözüm: e sayı cba olur. abc cba 495 100a 10b c 100c 10b a 495 100a 10b c 100c 10b 9 4 8 3 7 2 6 1 a 495 99a 99c 495 99 a c 495 495 a c 5 tir. 99 a c 5 bu 4 durum için her seferinde 10 farklı b değeri vardır. Buna göre; 10.4 40 sayı yazılır. 38
www.matematikkolay.net ab ve ba iki basamaklı sayılardır. ab ba 55 a b b a olduğuna göre, ab şeklinde yazılabilecek en büyük s ayı ile en küçük sayının toplamı kaçtı A) 178 B) 170 C) 1 r 4 ? 4 D) 130 E) 128 a b ab ba 55 a b b a ab ba 55 a b a b ab ba 55 a b 10a b 10b a 55 a b 11a 11b 55 a b 11 : Çözüm ab 55 5 9 6 3 2 a b a b 5a 5b 5b b 5a a 6b 4a 3b 2a 2a 3b dir. 2a 3b 96 32 128 bulunur. 42
www.matematikkolay.net ABB ve BAA üç basamaklı doğal sayılardır. ABB BAA 185 x y olduğuna göre, kaç farklı AB iki basamaklı doğal sayısı yazılabilir? A) 7 B) 9 C) 11 D) 13 E) 17 ABB BAA 185 x y 100A 10B B 100B 10A A 185 x y 111A 111B 185 x y 111 A B 185 x y Mar.37 : Çözüm A B 5. 37 5 3 10 6 15 9 x y 3 A B 5 x y A B 5 AB 14,23,32,41 A B 10 AB 19,28,37,46,55,64,73,82,91 A B 15 AB 69,78,87,96 4 9 4 17 sayı yazılır. 56
xx ve yy iki basamaklı doğal sayılardır. xx.yy 1936 olduğuna göre, iki basamaklı yazılabile cek xy sayılarının toplamı kaçtır? A) 52 B) 64 C) 72 D) 84 E) 154 www.matematikkolay.net xx.yy 1936 10.x x . 10.y y 1936 11.x.11.y 1936 121.x.y 1936 1936 x.y 16 dır. 121 Çarpımları 16 olan : Çözüm rakamlar; 2 ve 8, 4 ve 4 , 8 ve 2 dir. xy sayılarının toplamı 28 44 82 154 buluruz. 59
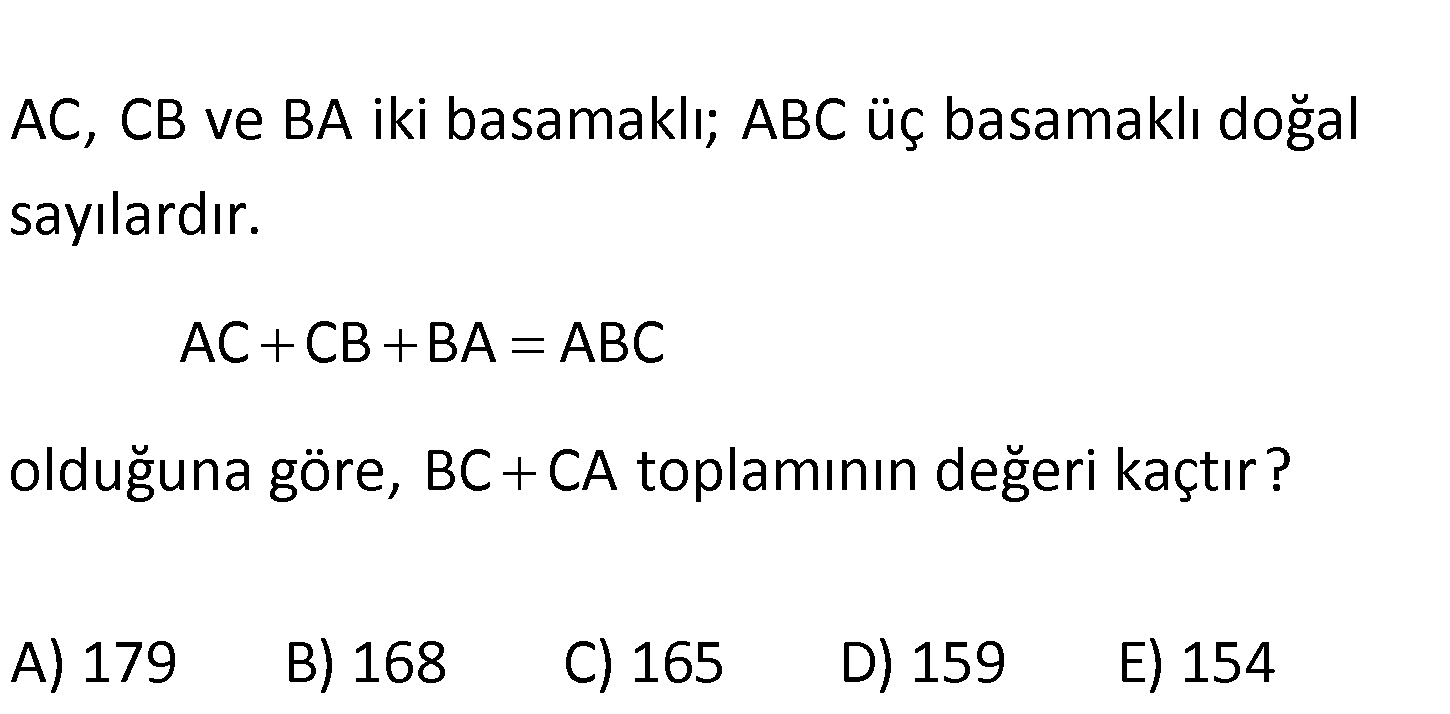
AC, CB ve BA iki basamaklı; ABC üç basamaklı doğal sayılardır. AC CB BA ABC olduğuna göre , BC CA toplamının değeri kaçtır? A) 179 B) 168 C) 165 D) 159 E) 154 www.matematikkolay.net AC CB BA ABC 10A C : Çözüm 10C B 10B A 100A 10B C 8 9 1 11A 10C B 100A 10C B 89A BC 98 CA 81 BC CA 98 81 179 bulunur. 62
2 K, L, M, N ve R farklı rakamlardır. K.L M N R koşuluna uygun en büyük KLMNR beş basamaklı sayısı için M L toplamı kaçtır? A) 11 B) 9 C) 8 D) 7 E) 6 www.matematikkolay.net 2 2 İki rakamın toplamı en fazla 18 olabilir. 9 9 Bu sebeple R , 18’den büyük olamaz. R 16 olurs : Çözüm 2 16 2 2 9 a R 4 olur. K.L M N R K.L 16 ise K 8, L 2 olur. KLMNR’yi en büyük hale getirebilmek için K 9 ile başlamalıydı. Çözümü başa almak gerekiyor. R 9 olursa R 3 olur. K.L M N R K.L 9 K 9 ve L 1 olur. M N 9 M 7 ve N 2 seçebiliriz. KLMNR 91723 olur. Rakam farklılığını sağladık. M L 7 1 8 buluruz. 64
ş İki basamaklı ab sayısı rakamları toplamının 7 katıdır. Bu şartlara uyan ab sayılarının toplamı a ağıdakilerden hangisidir? A) 42 B) 84 C) 126 D) 180 E) 210 2 1 4 2 6 3 8 4 ab 7 a b Çözümleyerek yazalım. 10a b 7a 7b 3a 6b a 2b dir. 21 42 63 84 210 bul : Çözüm uruz.

