Soru Sor sayfası kullanılarak Bölünebilme konusu altında Rakamlar değişitirldiğinde yeni kalan sayıyı bulma ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU


2.SORU
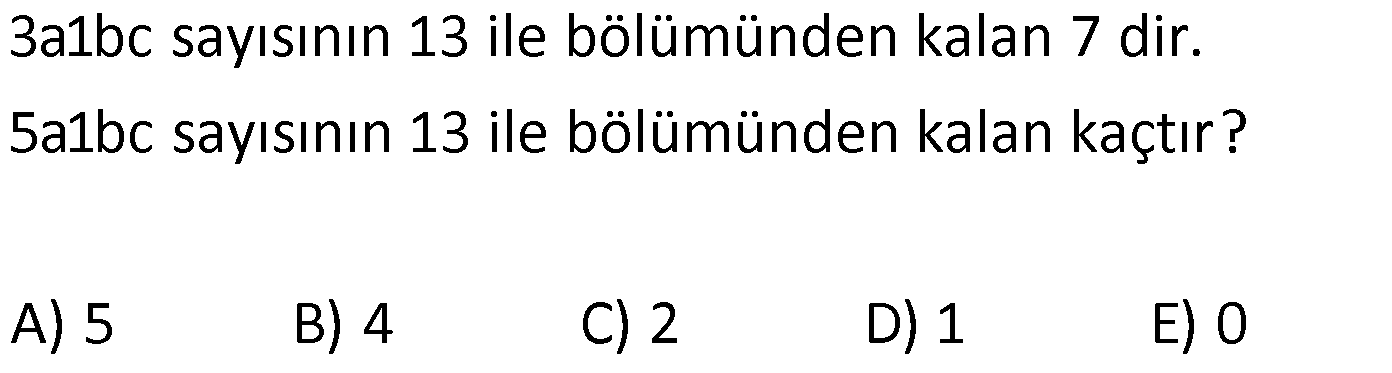

3.SORU


4.SORU
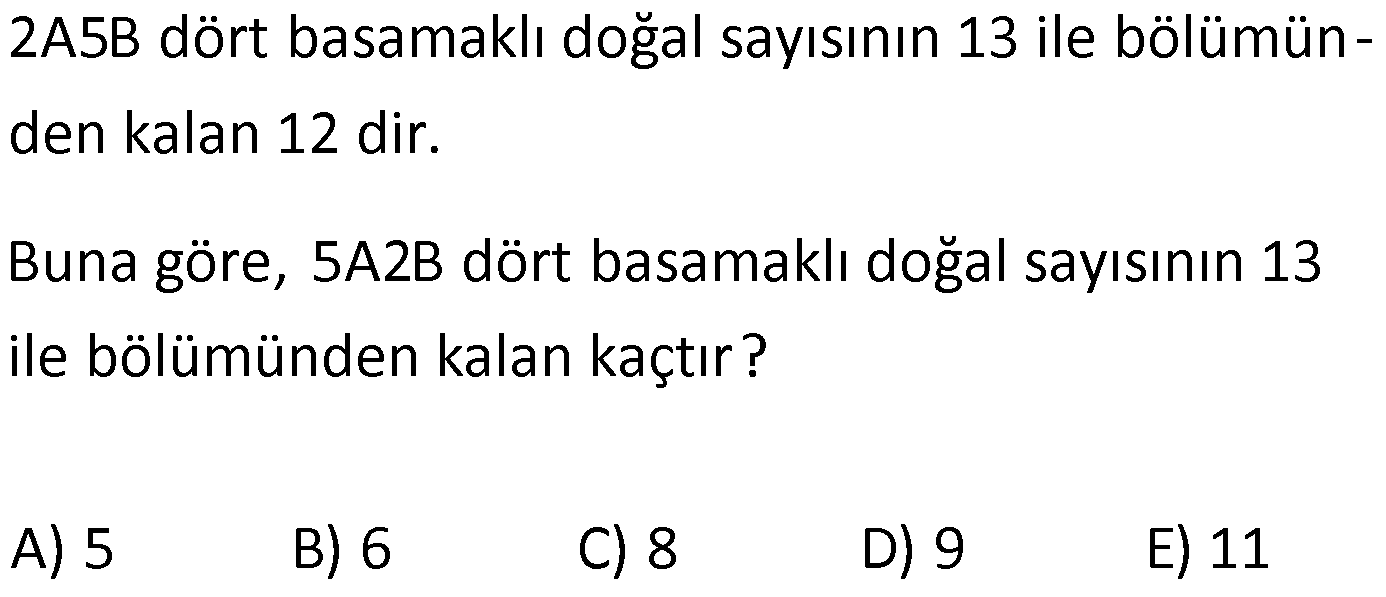

5.SORU


6.SORU


7.SORU


8.SORU
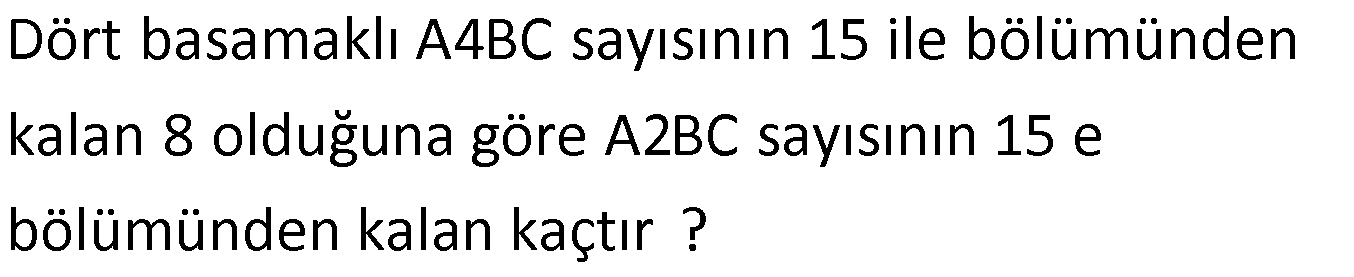

9.SORU


10.SORU


Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
2a3b sayısının 13 ile bölümünden kalan 1 olduğuna göre 3a2b sayısının 13 ile bölümünden kalan kaçtır? A) 3 B) 5 C) 7 D) 10 E) 12 www.matematikkolay.net : 3 2a3b 13k 1 2030 a0b 13k 1 2029 a0b 13k a0b 13k 2029 3a2b 3020 a0b 3020 13k 2029 3a2b 1 k 991 991’in 13 ile l bö Çözüm ümünden kalana bakmak yeterlidir. 991 13 91 76 81 78 3 3 bulunur. 25 3a1bc sayısının 13 ile bölümünden kalan 7 dir. 5a1bc sayısının 13 ile bölümünden kalan kaçtır? A) 5 B) 4 C) 2 D) 1 E) 0 www.matematikkolay.net 3a1bc sayısına 20000 eklenirse 5a1bc sayısı elde elde edilir.Buna göre; 5a1bc sayısının 13 ile bölümünden kal Çözüm: anı; 3a1bc 20000 toplamından hesaplayabiliriz. 3a1bc kalan 7 imiş. 20000 13 ile bölümünden kalan 6 dır. (Bölme işlemini ayrıntılı olarak yapmak gerekir. Klasik bir işlem olduğundan biz burada göster medik.) 3a1bc 20000 kalan 7 6 13 tür. 13 sayısı da 13’e tam bölüneceğinden kalan 0 buluruz. 29 4a3b dört basamaklı sayısı 19 ile bölündüğünde 7 kalanını veriyor. Buna göre, 3a4b sayısı 19 ile bölündüğünde kaç kalanını verir? A) 12 B) 10 C) 9 D) 7 E) 5 4a3b sayısı ile 3a4b sayısı arasındaki fark; 4a3b 3a4b 990 dır. 990’un 19’a bölümünden kalanı bulalım. 990 : Çözüm 19’a tam 38 2 bölünür kalan 7 kalan 2 950 40 Kalan 2 dir. Buna göre; 3a4b sayısının 19 ile bölümünden kalan; 4a3b 990 Kalan 7 2 5 buluruz. 33 www.matematikkolay.net 2A5B dört basamaklı doğal sayısının 13 ile bölümünden kalan 12 dir. Buna göre, 5A2B dört basamaklı doğal sayısının 13 ile bölümünden kalan kaçtır? A) 5 B) 6 C) 8 D) 9 E) 11 5A2B sayısı ile 2A5B sayısı arasındaki fark; 5A2B 2A5B 2970 dir. 2970’in 13 ile bölümünden kalanı bulalım. 29 : Çözüm 12 6 70 13 26 228 37 26 110 104 6 Kalan 6 dır. Buna göre 5A2B sayısının 13 ile bölümünden kalan; 5A2B 2A5B 2970 18’in 13 ile bölümünden kalan 5 bulunur. 42 www.matematikkolay.net xy42z ve xy64z beş basamaklı doğal sayılardır. xy64z sayısı 18 ile bölündüğünde kalan 15 olduğu – na göre, xy42z sayısının 18 ile bölümündeki kalan kaç olur? A) 11 B) 12 C) 13 D) 14 E) 16 kalan 15 xy42z xy00z 420 dir. xy64z xy00z 640 tır. Yani aralarındaki fark 640 420 220 dir. O zaman, xy64z xy : Çözüm 18’e tam bölünür kalan 15 kalan 4 42z 220 dir. Sadece kalanı hesaplaya – cağımız için 220’nin 18 ile bölümünden kalanı hesaplayalım. 220 216 4 kalan 4 tür. xy64z xy42z 220 xy42z kalan 11 olmalı ki eşitlik sağlansın. Cevap: A www.matematikkolay.net 48 www.matematikkolay.net Beş basamaklı 21ab5 sayısının 9 ile bölümünden kalan 2 dir. 813ab5 sayısının 9 ile bölümünden kalan kaçtır? A) 6 B) 5 C) 4 D) 3 E) 2 9k 2 rakamlar toplamı 9’un 21ab5 9k 2 813ab5 21ab5 792000 olur. Ayn : ı olanlar direk çıkarılırlar 813ab5 21ab 5 7 9200 0 Çözüm katı.Tam bölünür. Buna göre 813ab5 sayısının da 9 ile bölümünden kalan 2 bulunur. 50 abc nin 15 ile bölümünden kalan 2 olduğuna göre, 3abc7 nin 15 ile bölümünden kalan kaçtır? 15’e tam kalan 2 bölünür kalan 0 3abc7 3000 : 0 10.(abc) 7 dir. Kalanı bulmak için sadece ka lan sayılarla işlem y Çözüm apalım. 3abc7’den kalan 0 10.2 7 20 7 27 27′ yi 15’e bölersek 12 kalır. Cevap: 12 54 www.matematikkolay.net Dört basamaklı A4BC sayısının 15 ile bölümünden kalan 8 olduğuna göre A2BC sayısının 15 e bölümünden kalan kaçtır ? 15 ile 8 15 23 ü bölümünden kullanabiliriz. kalan 10 dur. A4BC : A0BC 400 dür. kalan 8 23 10 13 A0BC ‘nin Çözüm 13 15 ile bölümünden kalan 5 tir. 15 ile bölümünden kalan 13 olmalıdır. A2BC=A0BC+ 200 13 5 18 kalan 3 tür. 56 1abc5 beş basamaklı sayısının 23 ile bölümünden kalan 19 olduğuna göre, 5abc1 beş basamaklı sayı – sının 23 ile bölümünden kalan kaçtır? A) 8 B) 9 C) 13 D) 18 E) 19 İki sayı arasındaki : farka bakalım . 5abc1 _ 1abc5 3 9996 dır. 3999 6 23 _ 23 173 Çözüm Kalan 19 Kalan 22 8 169 161 89 69 206 184 22 Kalan 22 dir. 5abc1 1abc5 3996 19 22 41 dir. 41’in 23 ile bölümünden kalan 18 dir. Cevap: 18 www.matematikkolay.net 66 www.matematikkolay.net Dört basamaklı bir doğal sayı 15 ile bölündüğünde 11 kalanını veriyor. Bu sayının yüzler basamağı 5 artırılırsa oluşan sayı – nın 15 ile bölümünden kalan kaç olur? A) 1 B) 3 C) 7 D) 11 E) 13 Yüzler basamağı 5 a : rtınca bu sayı 500 büyür. 500’ün 15 ile böl ümünden kalanı bulalım . 5 0 15 45 33 Çözüm Kalan 11 Kalan 5 50 45 5 kalır. Sadece kalanlarla işlem yaparak, yeni kalan sayıyı bulabiliriz. A 500 11 5 16 16’nın 15 ile bölümünden kalan 1 dir. Cevap: 1 84

