Soru Sor sayfası kullanılarak Bölünebilme konusu altında Farklı sayılara bölünme durumları ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU


2.SORU
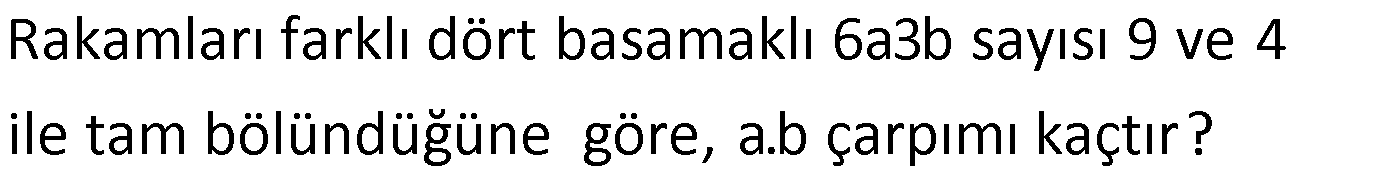

3.SORU


4.SORU


5.SORU
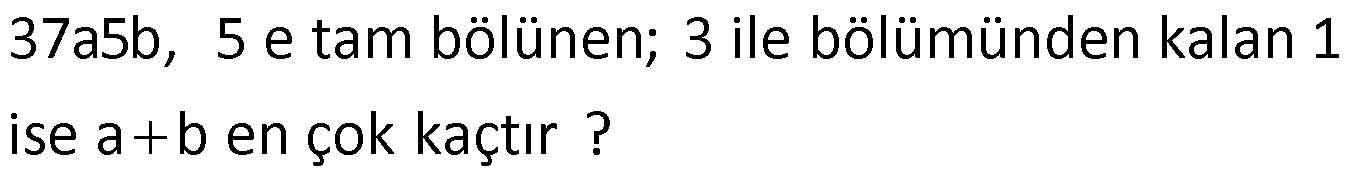

6.SORU


7.SORU


8.SORU


9.SORU


10.SORU


Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
www.matematikkolay.net Dört basamaklı 1a5b sayısı 3 ile tam bölündüğüne ve 5 ile bölümünden kalanı verdiğine göre, a nın alabileceği değerler toplamı kaçtır? 1a5b sayısının 5 ile bölümünden kalan 2 ise; b 2 veya 7 dir. 3’e tam bölünüyorsa, rakamların toplamı da 3’e bö : Çözüm lünmelidir. b 2 için; 1 a 5 2 3k 8 a 3k a 1 , 4 , 7 olabilir. b 7 için; 1 a 5 7 3k 13 a 3k a 2 , 5 , 8 olabilir. Buna göre; a değerlerinin toplamı: 1 2 4 5 7 8 27 buluruz. 9 Rakamları farklı dört basamaklı 6a3b sayısı 9 ve 4 ile tam bölündüğüne göre, a.b çarpımı kaçtır? 6a3b sayısı rakamları farklı 9 ve 4 ile bölünebilen bir sayı ise öncelikle 4ile bölünebilme kuralına bakalım. Çözüm: Sayının son iki basamağı 4’ün katı ise sayı 4’e tam bölünür. b 2 olsun. 6a32 sayısı 4 ile tam bölünür. b 6 olsun. 6a36 sayısı 4 ile tam bölünür fakat rakamları farklı olmaz.O halde b 2 dir. Şimdi 9 ile b 18 ölünebilme kuralına bakalım. 6a32 sayısının 9 ile bölünebilmesi için rakamları toplamı 9’un katı olmalı. 6 3 2 a 11 a 9’unkatı ise 18 olmalı. a 7 dir. a.b 7.2 14 bulunur. 21 www.matematikkolay.net A ve B bir rakam olmak üzere, 4A7B dört basamaklı sayısının 4 ile bölümünden kalan 2 dir. 8A3B dört basamaklı sayısının 9 ile bölümünden kalan 2 dir. Buna göre, A nın alabileceği değerler toplamı kaçtır? A) 15 B) 13 C) 12 D) 10 E) 8 4A7B sayısının 4 ile bölümünden kalan için son iki basamağın 4 ile bölümünden kalana bakmak yeterlidir. 4 il Çözüm: 0 4 8 e bölümünden kalan 2 ise; 7B sayısının 4 ile bölümünden kalan 2dir. B 0,4,8 değerlerini alabilir. 8A3B sayısının 9 ile bölümünden kalan 2 ise sayının rakamları toplamının 9ile bölümünden kalan 2 olmalı. 2 8 3 A B 9k 2 11 A B 9k 2 11 A B 20 A B 9 dur. B 0 A 9 B 4 A 5 B 8 A 1 dir. 9 5 1 15 bulunur. 22 www.matematikkolay.net A sayısı 5 e bölündüğünde kalan 3 A sayısı 7 ye bölündüğünde kalan 2 ise A sayısının 35 e bölünümünden kalan kaçtır? : A 5k 3 7z 2 dir. Her tarafa öyle bir sayı ekleyelim ki hem 5’in hem de 7’nin katını elde edelim. Örneğin Çözüm 12 sayısı, bunun için uygundur. A 12 5k 15 7z 14 olur. A 12 5(k 3) 7(z 2) A 12 sayısı, hem 5’in hem de 7’nin katı ol – duğundan 35’in de katı bir sayıdır. A 12 35x ise; A sayısından kalan 23 olmal ıdır. 27 37a5b, 5 e tam bölünen; 3 ile bölümünden kalan 1 ise ab en çok kaçtır ? 5’e bölünebilmesi i : çin son rakam ya 0, ya da 5 olmalıdır. b 0 veya b 5 tir. b 5 seçelim. 37a55 sayısının rak aml Çözüm arı toplamı da 3’ün katından 1 fazla olmalıdır. 3 7 a 5 5 3k 1 20 a 3k 1 a 8 olabilir. a b 5 8 13 buluruz. en çok www.matematikkolay.net 76 2525252 7 basamaklı sayının 11 ile bölümünden kalan x , 3 ile bölümünden kalan y ise x , y çarpımı kaçtır : 2525252 2 2 2 2 5 5 5 8 15 7 dir. 7 11 4 11 ile bölümünden kalan 4 tür. 2525252 2 5 2 5 2 5 2 2 Çözüm 3 3 ile bölümünden kalan 2 dir. O halde; x.y çarpımı 4.2 8 buluruz. 77 www.matematikkolay.net abc üç basamaklı sayısı 2’ye bölündüğünde 1, 5’e bölündüğünde 3 kalanını veriyor. Bu abc sayısı en büyük kaç olur? abc 2x 1 5y 3 : şek linde yazabi liriz. Her taraf tan 3 çık aralım. abc 3 2x 2 5y olur. abc 3 2 x 1 5y abc’ni n Çözüm 3 eksiği hem 2’nin hem de 5’in katıdır. Yani 10’un tam katıdır. ekok(2,5) 10 abc 3 10k dır. En büyük üç basamaklı abc sayısı için k 99 seçelim. abc 3 990 abc 993 buluruz. 85 ab4 rakamları birbirinden ve sıfırdan farklı üç basamaklı sayıdır. Bu sayının 9 ile bölünebilen en büyük değer ile 8 ile bölünebilen en küçük değer arasındaki fark kaçtır? A) 750 B) 770 C) 790 D) 810 E) 826 www.matematikkolay.net Sayının 9 ile bölün : ebilen en büyü k sayı olması için; a 9 b 5 olur. abc 954 8 il e bölün en en küçük değer için ik i Çözüm basamaklı 8 ile bölünebilen en büyük sayı 96’dır. 96 8 104 En küçük 3 basamaklı sayı olur. Fakat sayılar sıfırdan farklı olduğu için Sayıyı 1’ler basamağını bozmadan 8’in katlarını ekleyerek bulalım. 40 eklersek b 4 olur farklı olmaz. 80 eklersek b 8 olur. Sayı 184 olur. 954 184 770 bulunur. 92 www.matematikkolay.net Rakamları farklı dört basamaklı 720x sayısı 9 ile tam bölünebilmektedir. Buna göre, bu sayının 11 ile bölümünden kalan kaç – tır? A) 9 B) 5 C) 3 D) 1 E) 0 9 ile tam bölüne : biliyorsa 7 0 2 x 9k 9 x 9k x 0 ya da 9 olabilir. 702x rakamları farklı ise x 9 olur. x Çözüm 0 olamaz. O halde bu sayı 7029 dur. 11 ile bölünebilme için , – yazarak kalanı bulalım. 7029 9 0 7 2 9 9 0 dır. 11 ile bölümünden kalan 0 dır. 103 x sayısı 18 ile y sayısı 15 ile tam bölünmektedir. Buna göre, 3x 4y toplamı aşağıdakilerden hangisi – ne kesinlikle tam bölünür? A) 6 B) 8 C) 10 D) 12 E) 15 www.matematikkolay.net x 18a y 15b şe : klinde i ki sayıdır. Buna göre; 3x 4y 3.18a 4.15b 48a 60 b dir. Ortak paranteze alm Çözüm aya çalışalım. 48a 60b 6 12a 5b 6’ya tam bölünür. 105


9. soru hatalı soruda 720x yazıyor ama 702x üzerinden işlem yapılıyor.
Uyarınız için teşekkürler. Sorudaki yazım hatası düzeltildi.