Soru Sor sayfası kullanılarak Bölünebilme konusu altında 15 ile bölünebilme
ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
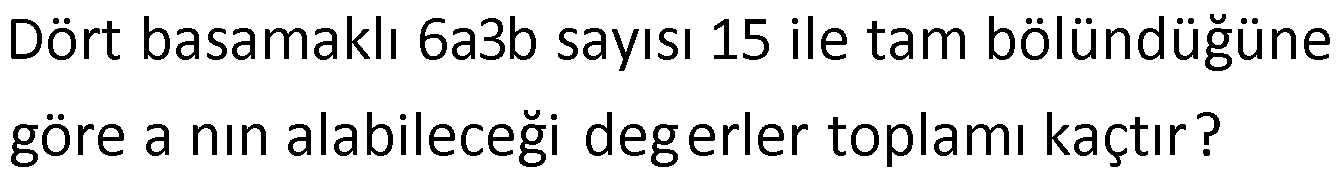

2.SORU


3.SORU

4.SORU


5.SORU


6.SORU


Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
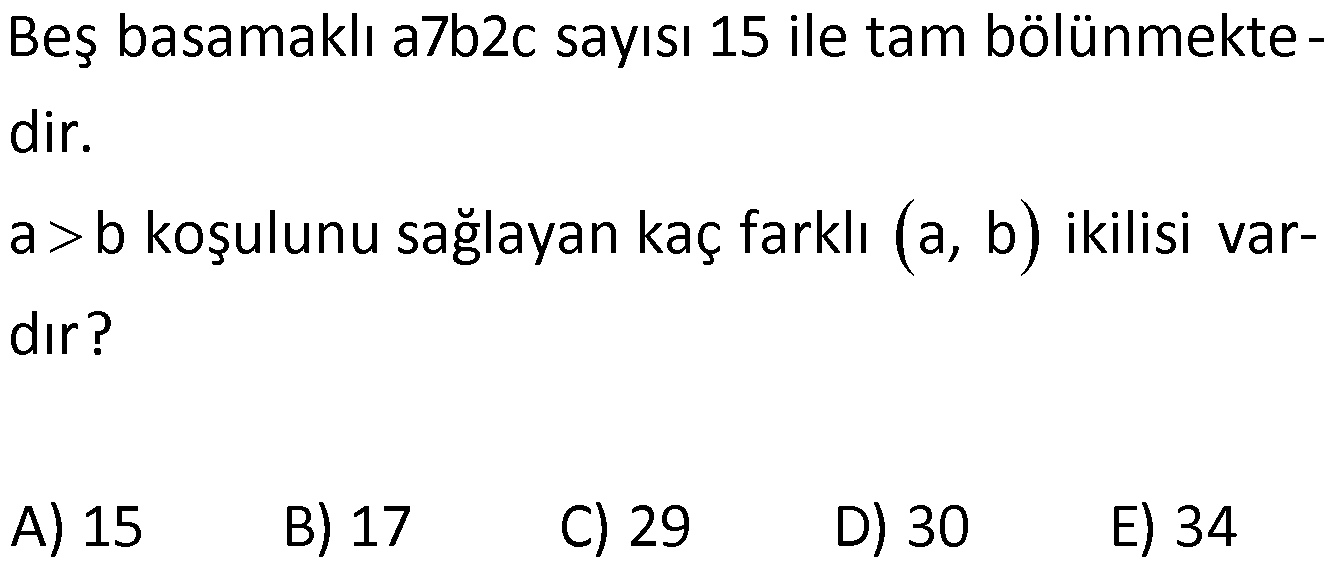
Dört basamaklı 6a3b sayısı 15 ile tam bölündüğüne göre a nın alabileceği deg erler toplamı kaçtır? www.matematikkolay.net : 15 sayısı 3 ve 5’in çarpımıdır. Buna göre 6a3b sayısı hem 3’e hem de 5’e tam bölünür. 5’e bölünmesi için b 0 y Çözüm a da 5 olabilir. b 0 olduğunda 6a30 sayısının 3’e bölünebilmesi için rakamları toplamı 3’ün katı olmalıdır. a 9 3’ün katı ise a 0,3,6,9 olabilir. b 5 olduğunda 6a35 sayısının 3’e bölünebilmesi içi n rakamları toplamı 3’ün katı olmalıdır. a 14 3’ün katı ise a 1,4,7 olabilir. Buna göre; a değerleri toplamı 0 3 6 9 1 4 7 30 buluruz. 14 ab biçimindeki bir sayının 15 ile çarpımı x5y biçiminde üç basamaklı bir sayıdır. Buna göre, x y toplamının kaç farklı değeri vardır? A) 3 B) 4 C) 5 D) 6 E) 7 www.matematikkolay.net x5y sayısı 15’in katı ise; hem 3’e hem de 5’e tam bölünebilmelidir. 5’e bölünüyorsa y 0 veya y 5 tir. y 0 : Çözüm 0 5 olursa; x 5 0 3k olmalıdır. x 1, 4, 7 olabilir. x y 1,4,7 olur. y 5 olursa x 5 5 3k x 10 3k x 2,5,8 olabilir. x y 7,10,13 olabilir. Tüm x y değerleri 1,4,7,10,13 5 farklı değer. 31 Beş basamaklı a7b2c sayısı 15 ile tam bölünmekte – dir. a b koşulunu sağlayan kaç farklı a, b ikilisi vardır? A) 15 B) 17 C) 29 D) 30 E) 34 www.matematikkolay.net 15’e bölünen bir sayı hem 3’e hem de 5’e tam bölünür. Son basamaktaki sayı c 0 ya da 5 olmalıdır. Ayrıca bu sa : Çözüm 3’ün katı yının rakamları toplamı 3’ün katı olmalıdır. c 0 olursa, a7b20 a 7 b 2 3k a b 9 3k a b toplamı da 3’ün katıdır. a b ise (a,b) (2,1),(3,0),(4,2),(5,1),(5,4),(6,0),(6,3), (7,2),(7,5),(8,1),(8,4 3 ile bölümünden kalan 2 dir. ),(8,7),(9,0),(9,3),(9,6) 15 farklı ikili yazılabilir. c 5 olursa, a7b20 a 7 b 2 5 3k a b 14 3k a b toplamı da 3’ün katından 1 fazladır. a b ise (a,b) (1,0),(3,1),(4,0),(4 ,3),(5,2),(6,1),(6,4), (7,0),(7,3),(7,6),(8,2),(8,5),(9,1),(9,4),(9,7) 15 farklı ikili yazılabilir. Toplam 30 farklı (a,b) ikilisi yazılabilir. 45 2ab3c sayısının 15 ile bölümünden kalan 4 tür. Buna göre, a b c toplamının en büyük değeri kaçtır? A) 17 B) 21 C) 22 D) 26 E) 27 www.matematikkolay.net 15 sayısı 3 ve 5’in : çarpımıdır. 15 ile bölündüğünde 4 kalanını veriyorsa 5 ile bölünd üğ ünde de 4 kala nını verir Çözüm . Sayının son rakamı c 4 veya 9 dur. a b c en büyük olması için, c 9 seçelim. 15 ile bölündüğünde 4 kalanını veriyorsa 3 ile bölündüğünde de 1 kalanını verir.(4’ün 3 ile bölümünden kalan 1 dir.) 2ab3c sayıs 9 17 olur en fazla 8 9 9 ınının rakamları toplamı 3’ün katından 1 fazla olmalıdır. 2 a b 3 c 3k 1 5 a b c 3k 1 14 a b 3k 1 O halde; a b c 8 9 9 26 buluruz. 69 Dört basamaklı 8x3y sayısının 15 ile bölümünden elde edilen kalan 9 dur. Buna göre x’in alabileceği kaç değer vardır? www.matematikkolay.net : 15 sayısı 3 ve 5’in çarpımıdır. 15 ile bölümünden kalan 9 ise; 9’un 5 ile bölümün- 5 ile bölümünden kalan 4 tür. Çözüm den kalan 4 tür. O halde son basamak y 4 veya y 9 olmalıdır. 15 ile bölümünden kalan 9 ise; 9’un 3 ile bölümün- 3 ile bölümünden kalan 0 dır. den kalan 0 dır. 8 x 3 y 3k olmalıdır. y 4 olurs a 8 x 3 4 3k 15 x 3k x 0,3,6,9 olabilir. y 9 olursa 8 x 3 9 3k 20 x 3k x 1,4,7 olabilir. O halde x sayısı 7 farklı değer alabilir. 78 Rakamları farklı, dört basamaklı 7x3y sayısının 15 ile bölümünden kalan 12 olduğuna göre, x ‘in alabileceği kaç farklı değer vardır? www.matematikkolay.net : 15 sayısı 3 ve 5’in çarpımıdır. 15 ile bölümünden kalan 12 ise; 5 ile bölümünden kalan 2 dir. 12’nin 5 ile bölü Çözüm münden kalan 2 dir. O halde son basamak y 2 veya y 7 olmalıdır. Ancak y 7 olamaz. Çünkü 7x3y sayısı rakamları farklı olmaz. 15 ile bölümünden kalan 12 ise; 3 ile bölümünden kalan 0 dır. 12’nin 3 ile bölüm ünden kalan 0 dır. 7 x 3 y 3k olmalıdır. y 2 idi. 7 x 3 2 3k 12 x 3k x 0,3,6,9 olabilir. Ancak x 3 olamaz. Rakam farklılığını bozuyor. x 0,6,9 olabilir. 3 farkl ı değer alabilir. 79

