Soru Sor sayfası kullanılarak Bölünebilme konusu altında 6 ile bölünebilme ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
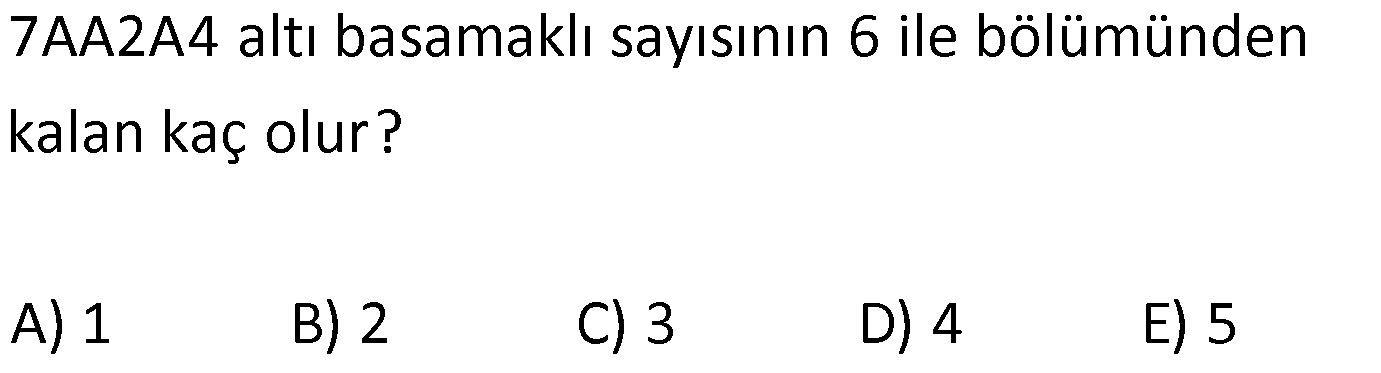

2.SORU


3.SORU


Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
7AA2A4 altı basamaklı sayısının 6 ile bölümünden kalan kaç olur? A) 1 B) 2 C) 3 D) 4 E) 5 www.matematikkolay.net 7AA2A4 700204 AA0A0 AA0A0 sayısı çift olduğundan 2′ ye tam bölünür. Rakamları toplamı 3A, 3’e tam bölündüğünden : Çözüm kalan 0 hem 3’e hem de 2’ye tam bölünür. 3’e de tam bölünür.Buna göre bu sayının 6 ile bölümünden kalan 0’dır. 7AA2A4 700204 AA0A0 700204 sayısının 6 ile bölümünden kalanı bulmak yeterlidir. 700204 700200 4 Kalan 4 bulunur. 35 www.matematikkolay.net Sıfırdan ve birbirinden farklı A, B, C rakamlarının yerleri değiştirilerek elde edilen 6 sayı toplanıyor. Bu toplamla ilgili aşağıdakilerden hangisi kesinlik – le doğrudur? A) 15 ile tam bölünür. B) 6 ile tam bölünür. C) 10 ile tam bölünür. D) 9 ile tam bölünür. E) 12 ile tam bölünür. ABC ACB BAC : BCA C AB CBA Her r akam 2’şer ker e yüzler , onlar ve birler basamağındadır. Toplarsak ; 222 A B C Çözüm yapar. 222 sayısı 6 ile tam bölünür. Çünkü hem 2’nin hem de 3’ün tam katıdır. Cevap: B 100 3 3 a doğal sayısının 12 ile bölümünden kalan 5, b doğal sayısının 18 ile bölümünden kalan 4 tür. Buna göre, a .b a.b toplamının 6 ile bölümünden kalan kaçtır? A) 0 B) 1 C) 2 D) 3 E) 4 www.matematikkolay.net a doğal sayısının 1 : 2 ile bölümünd en kalan 5 ise, 6 ile bölümün den kalan da 5′ tir. Örn eğ in a sayısı 17 olsun. 12 Çözüm ile bölümünden kalan 5′ tir. 6 ile bölümünden kalan da 5′ tir. İşlem yaparken a 5 kabul edebiliriz. b’nin 18 ile bölümünden kalan 4 ise, 6 ile bölümünden kalan da 4 tür. b 4 diyerek işlem yapabiliriz. O 3 3 3 3 halde; a .b a.b 5 .4 5.4 125.4 5.64 500 320 820 820’yi 6 ile bölersek kalanı da 4 buluruz. 75

