Soru Sor sayfası kullanılarak Fonksiyonlar konusu altında Ters fonksiyondan asıl fonksiyonu bulma ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU


2.SORU
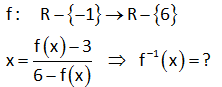

3.SORU


4.SORU


Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
1 1 5 1 f : R R olmak üzere, 2 2 f x 3 x 2f x 5 olduğuna göre, f x fonksiyonu aşağıdakilerden hangisidir? x 1 x 3 x 3 A) B) C) 3x 2 2x 5 3x 2 x 3 5x 3 D) E) 2x 5 x 1 1 1 1 1 Bize verilen ifadede ters fonksiyonun tersi alınmış. f (x) f(x) olur. Buna göre; f (x) 3 x 3 x f(x) buluruz. 2f (x) 5 2x : 5 Çözüm 54 1 f : R 1 R 6 f x 3 x f x ? 6 f x 1 1 f x 3 x 6 f x Fonksiyonun tersi alınırken x, f x cinsinden yazılır. Sonra x, yerine f x ve f x yerine x yazılır. Fonksiyonun tersi alınmış.Sadece f x yerine x yazmamız yeterlidir. x 3 f x bulunu 6 x : r. Çözüm 160 1 1 f : R R 0 olmak üzere, 2 2.f x 2 2x 1 f x olduğuna göre, f 6 değeri kaçtır? 1 1 1 A) B) C) D) 2 E) 4 4 3 2 www.matematikkolay.net 1 1 2f x 2 2x 1 f x 2f x 2 2f x 2 f x 2x 1 f x f x f x 2 f x f x 2 x 2 2f x x 2 f x bulunur. 2x 6 2 4 1 f 6 bulunur. 2.6 12 3 : Çözüm 170 1 f x fonksiyonu birebir ve örtendir. 3 2f x x f x 1 olduğuna göre, f 2 kaçtır? A) 5 B) 6 C) 7 D) 8 E) 9 www.matematikkolay.net 1 1 3 2f x x ifadesinde x, f x cinsinden f x 1 yazılmış. Yani fonksiyonun tersi alınmış. 3 2x f x dir. x 1 3 2. 2 3 4 f 2 7 bulunur. 2 : 1 1 Çözüm 319

