Soru Sor sayfası kullanılarak Fonksiyonlar konusu altında Bileşke fonksiyon ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
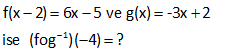

2.SORU
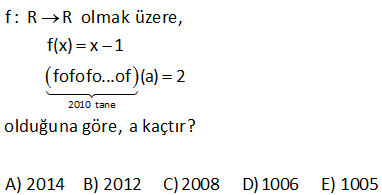

3.SORU


4.SORU


5.SORU


6.SORU


7.SORU
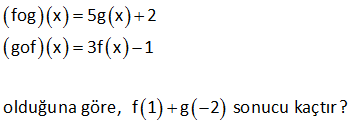
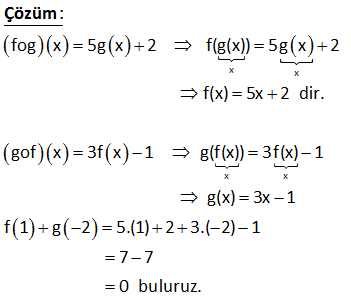
8.SORU
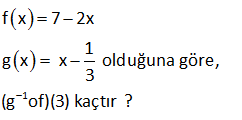

9.SORU

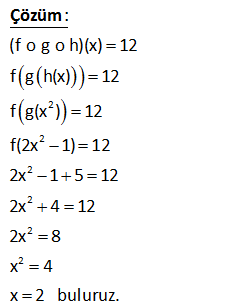
10.SORU
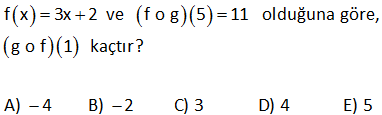
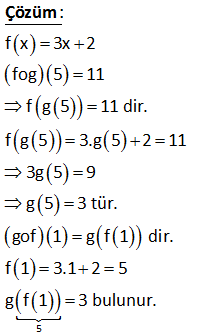
11.SORU
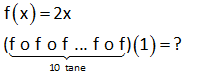

Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
1 f(x 2) 6x 5 ve g(x) -3x 2 ise (fog )( 4) ? 1 1 1 1 (fog )( 4) fonksiyonu f(g ( 4)) demektir. İlk önce g ( 4) u bulalım. g(x) 4 değeri hangi x için sağlanır. g(x) -3x 2 4 3x 6 x 2 dir. Buna göre; g(2) 4 ise g ( 4) 2 f( : g Çözüm 1 2 1 ( 4)) f(2) Şimdi f(2) yi bulalım. f(x 2) 6x 5 x 2 2 için x 4 olmalıdır. 6x 5 6.4 5 19 Yani f(2) 19 buluruz. Buna göre; (fog )( 4) 19 dur. www.matematikkolay.net 4 www.matematikkolay.net 2010 tane f : R R olmak üzere, f(x) x 1 fofofo…of (a) 2 olduğuna göre, a kaçtır? A) 2014 B) 2012 C)2008 D)1006 E) 1005 2010 tane Adım adım bileşke fonksiyonu yapalım. 1. f(a)=a 1 2. f(f(a))=f(a 1) a 2 3. f(f(f(a))) f(f(a 1))=f(a 2) a 3 : : 2010. (fofofo…f)(a) a 2010 dur. a 2010 2 ise a=2012 dir. Doğru C : Çözüm evap: B şıkkı 6 1 Tanımlı olduğu aralıkta f(x) ve h(x) fonksiyonları veriliyor. (foh)(x) 4x 1 (h of)(x) 3x 5 olduğuna göre, (fof)(2) kaçtır? A) 5 B) 6 C) 7 D) 8 E) 9 1 1 1 (foh)(x) 4x 1 (h of)(x) 3x 5 İkinci bileşke fonksiyonu, sağdan gelecek şekilde birinci fonksiyon ile birleştirip, h ile h fonksiyon larının birbirini yok etmesini sağlayalım. (foh) o (h of) (x) : Çözüm 1 (4x 1) o (3x 5) (fohoh of)(x) 4.(3x 5) 1 (fof)(x) 12x 20 1 (fof)(x) 12x 19 (fof)(2) 12.2 19 24 19 5 buluruz. 18 2 1 Tanımlı oldukları aralıklardaki f ve h fonksiyonları için, (x 1)f(x) (x 5).(foh)(x) 2x 8x 2 olduğuna göre, h (5) kaçtır? A) 5 B) 4 C) 3 D) 2 E) 1 2 2 0 4 (x 1)f(x) (x 5).(foh)(x) 2x 8x 2 x 1 için (1 1)f(x) (x 5).(foh)(1) 2.1 8.1 2 4.(foh)(1) 2 8 2 4.(foh)(1) 8 (foh)(1) 2 dir. (bu cepte) x 5 için bakalım. 4f(5) 2.25 8.5 2 4f(5) 8 f(5) : 2 Çözüm 5 1 dir. (foh)(1) 2 yi de bulmuştuk.Yani; f(h(1)) 2 h(1) 5 diyebiliriz. Burdan da; h (5) 1 buluruz. www.matematikkolay.net 27 1 1 f ve g birebir ve örten fonksiyonlardır. (f og)(x) 3x 5 ve g (6) 2 olduğuna göre, f(11) değeri kaçtır? A) 4 B) 6 C) 11 D)23 E) 36 www.matematikkolay.net 1 1 1 g (6) 2 g(2) 6 dır. (f og)(x) 3x 5 f (g(x)) 3x 5 f(3x 5) g(x) dır. x 2 yerine koyalım. f(3.2 5) g(2) f(11) g(2) 6 dır. f(11) 6 bulur : u Çözüm z. 33 Şekilde f(x) fonksiyonunun grafiği görülmektedir. g(x) “Taralı bölg enin alanı” şeklinde bir fonksiyon tanımlanıyor. (fog)(x) 162 olduğuna göre, x kaçtır ? A) 8 B) 9 C) 10 D)11 E) 12 www.matematikkolay.net f(x) 2x fonksiyonu bize verilmiş g(x) fonksiyonunu oluşturalım. x 2 g(x) Taralı Bölg enin : Alanı Çözüm x 2 2 2 x 2 2 x (fog)(x) 162 f(g(x)) 162 2.x 162 x 81 x 9 buluruz. (x eksenin pozitif tarafında olduğundan) Doğru Cevap : B Şıkkı 34 fog x 5g x 2 gof x 3f x 1 olduğuna göre, f 1 g 2 sonucu kaçtır? x x x x : fog x 5g x 2 f(g(x)) 5g x 2 f(x) 5x 2 dir. gof x 3f x 1 g(f(x)) 3f(x) 1 g(x) 3x 1 f 1 g 2 5.(1) 2 3.( 2 Çözüm ) 1 7 7 0 buluruz. 45 1 f x 7 2x 1 g x x olduğuna göre, 3 (g of)(3) kaçtır ? 1 1 1 1 1 1 : (g of)(3) g f(3) İlk önce f(3) ü bulalım. f(3) 7 2x 7 2.3 7 6 1 dir. g f(3) g 1 olur. g(x)’i 1 yapan x değerini bulalım. 1 g x x 3 1 1 x 3 1 4 1 x x tür. 3 3 4 O halde; g 1 tür. 3 Cevap: (g of Çözüm 4 )(3) buluruz. 3 67 www.matematikkolay.net 2 Gerçel sayılar üzerinde tanımlı f, g ve h fonksiyonları; f x x 5 g x 2x 1 h x x biçiminde tanımlanıyor. f o g o h x 12 olduğuna göre, x değeri kaç olabilir? A) 1 B) 2 C) 3 D) 4 E) 5 2 2 2 2 2 2 (f o g o h)(x) 12 f g h(x) 12 f g(x ) 12 f(2x 1) 12 2x 1 5 12 2x 4 12 2x 8 x 4 x 2 buluruz. : Çözüm 138 f x 3x 2 ve f o g 5 11 olduğuna göre, g o f 1 kaçtır? A) 4 B) 2 C) 3 D) 4 E) 5 5 f x 3x 2 fog 5 11 f g 5 11 dir. f g 5 3.g 5 2 11 3g 5 9 g 5 3 tür. gof 1 g f 1 : dir. f 1 3.1 2 5 g f 1 3 bulunur. Çözüm 150 10 tane f x 2x (f o f o f … f o f) 1 ? www.matematikkolay.net 2 3 4 10 10 f(x) 2x ise; f(1) 2.1 2 dir. Buna tekrar f(x) uygulanırsa f(2) 2.2 4 olur. Bu da 2 dir. 2.adım f(4) 2.4 8 2 3.adım f(8) 2 4.adım … 10.adımda 2 olur. fofofof .f : .. Çözüm 10 tane (1) 2 buluruz. 276

