Soru Sor sayfası kullanılarak İşçi Problemleri konusu altında Harfli İşçi Problemleri ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU


2.SORU


3.SORU

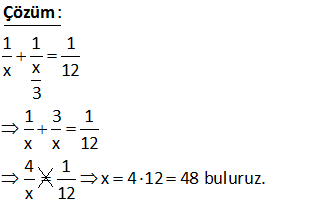
4.SORU


5.SORU


6.SORU


7.SORU


8.SORU


9.SORU


10.SORU


11.SORU


Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Çıkmış Sorular İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
Bir işi; Adnan ve Beyza birlikte 2x saatte yapıyor. Suzan tek başına 3x saatte yapıyor. 1 Bu işi 3 kişi birlikte yaparsa Adnan tüm işin ini 5 yapmış oluyor. , Buna göre bu işi üçü beraber tamamlandığ ? 11 12 5 7 2 A) B) C) D) E) 20 25 12 10 5 ında Beyza tüm işin kaçta kaçını yapmıştır Adnan ve Beyza beraber 2x saatte Suzan tek başına 3x saatte ise Suzan’ın hızına 2V dersek; Adnan ve Beyza 3V’dir. Toplam iş 5V’liktir. Hepsi beraber işi yapınca Adnan 5’te 1’ini bitiriyorsa A : dnan’ı Çözüm n hızı V’dir. Buna göre Beyza: 3V-V=2V hızındadır. 2V 2 Beyza işin = ini yapar. 5V 5 2 Bir tekstil atölyesinde iki dikiş makinesi vardır. a ve b birer tamsayı olmak üzere, bir gömleği bu makinelerden biri a saatte diğeri b saatte dikebiliyor. ab tane gömleği makinelerden biri 43 saat da , ? A) 12 B) 14 C) 20 D) 22 E) 33 ha kısa sürede dikebildiğine göre a aşağıdakilerden hangisi olabilir www.matematikkolay.net Bir gömleği a saatte dikebilen makine, a b tane gömleği (a b).a saatte bitirir. Bir gömleği b saatte dikebilen makine, a b tane gömleği (a b).b saatte bitirir. Aradaki fark 43 saat : ise; (a b). Çözüm 2 a (a b).b 43 a ab ab 2 2 2 1 43 1×43 b 43 a b 43 (a b)(a b) 43 a b 1 a b 43 2a 44 a 22 dir. 15 x Hakan bir işi x günde, Yiğit ise aynı işi günde 3 yapmaktadır. , ‘ ? İkisi birlikte bu işi 12 günde bitirebildiklerine göre x in değeri kaçtır 1 1 1 x x 12 3 1 3 1 x x 12 4 x : Çözüm 1 x 4 12 48 buluruz. 12 www.matematikkolay.net 16 Üç işçi birlikte işe başlıyor. I. işçi günlük x br, II. işçi günlük y br ve III. işçi günlük z br iş yapıyor. I. işçi kapasitesini %10, II.işçi kapasitesini %30 artırıp, III. işçi kapasitesini %20 azaltırsa günlük yapılan iş miktarı değişmiyor? , , ? A) 9y 2z B) z y C) 2y z D) 3z 2y E) 6z y Buna göre x 6y olduğu bilindiğine göre y ve z arasındaki bağıntı nedir 6y x y z 1,1x 1,3y 0,8z bağıntısını kurabiliriz. 0,2z 0,1x 0,3y olur. Her tarafı 10 la genişletelim. 2z x 3y olur. 2z 6y 3y 2z 9y 9y 2z buluruz. : Çözüm 21 Bir grup işçi bir işi a 2 günde bitiriyor. Aynı işçi- 1 ler a 6 günde bu işin ‘ünü bitiriyor. 3 ? Aynı işçiler 6 gün çalışırsa işin kaçta kaçı biter : a 2 gün, a 6 nın 3 katıdır. Buna göre; a 2 3.(a 6) a 2 3a 18 20 2a a 10 dur. Demek ki bu işçiler işin tamamını a 2 12 günde 1 bitiriyorlarmış. 6 gün daha çalışırlırsa bu işin 2 sini daha biti Çözüm (2) (3) rirler. Toplamda bu işin; 1 1 1 1 2 3 5 sı biter. 3 2 3 2 6 6 6 5 Cevap: 6 31 www.matematikkolay.net x ve y pozitif tam sayılardır. Orhan bir işi x günde Efe aynı işi y günde yapabilmektedir. İkisi birlikte işi yapmaya başladıklarında; Orhan işi tek başına yapma süresinin 3 eksiği gün, Efe işi tek başına yapma süresinin 2 eksiği gün çalışırsa işin tamamı bitiyor. , ? A) 9 B) 10 C) 11 D) 12 E) 13 Buna göre x y toplamı en az kaçtır x 3 y 2 1 x y x 3 y 2 1 x x y y 3 2 1 1 1 x y 3 2 2 1 x y 3 2 1 x y İki rasyonel sayının toplamı 1 ise ikisi de 1 ayrı ayrı dir. 2 3 1 x 6 dır. x 2 2 1 y 4 tür. y 2 x y 10’dur. : Çözüm 90 Bir şey x işçisi z günde, y işçisi t günde yapabilmek – tedir. x işçisi 4 gün y işçisi 8 gün çalıştıklarında işin 2z si bitmiştir. Buna göre z t toplamı en az kaçtır? t z ve t tamsayıdır. www.matematikkolay.net t z 1 İşi x işçisi z günde yaparsa günde ‘sini yapar. z 1 İşi y işçisi t günde yaparsa günde ‘sini yapar. t 1 1 2z 4 8. dir. z t t 4 8 2z her tarafı 2 ye bölelim. z t t 2 4 z z t t 2t 4z z. : t Çözüm z t 2 2 2t 4z z 2t z 4z 2t z z 4 z 4 ve çift olmalı. z 6 için; 2t z z 4 2 t 6.2 t 6 dır. z t 6 6 12 bulunur. 95 Bir fabrikada bir işçi x saatte y tane futbol topu üretebiliyor. Aynı sürede, Bu işçinin k katı futbol topu üretebilen başka bir işçi, y tane futbol topu nun kaç saatte üretebilir? www.matematikkolay.net y İlk işçi 1 saatte kadar top üretebilir. x ky İkinci işçi ise 1 saatte kadar top üretebilir. x y tane topu ise; y saatte üretebilir. Bunu düzenleyelim. ky x : y Çözüm k y x buluruz. k x 101 www.matematikkolay.net Bir işi x işçi 4x 8 günde tamamlamaktadır. Bu işçilerden 4 tanesi günün yarısını çalışarak geçirdiğine göre, ? A) 2 B) 2x C) 2x 1 D) 3x 1 E) 4x işin bitmesi için geçen süre aşağıdakilerden hangisidir 4 işçi yarım gün çalışırsa bunlar tam gün çalışan 2 işçi gibi olurlar. Yani 2 işçi bu işten ayrılmıştır, diyebiliriz. x işçi 4x 8 günde bitiriyorsa x 2 işçi y günde bitirir : Çözüm x.(4x 8) x.4 (x 2) Ters O. y x 2 x 2 4x buluruz. 103 www.matematikkolay.net 2a a Bir işi Seda , Kübra saatte yapmaktadır. 5 3 , ? 22 25 A) B) 8 C) D) 21 E) 22 3 3 İkisi birlikte aynı işi 4 saatte yapabildiğine göre Kübra bu işi yalnız başına kaç saatte yapar 4 4 1 dir. İş denklemi 2a a 5 3 20 12 1 2a a 10 12 1 a a 22 1 a 22 dir. a a 22 Kübra buluruz. 3 3 : Çözüm 109 www.matematikkolay.net Bir fabrikada a b adet makinenin hepsi eşit kapasitelidir. Bu fabrikadaki makinelerin a adeti çalıştırılmazsa iş 14 saatte, b adeti çalıştırılmazsa iş 24 saatte bitiyor. Bu fabrikadaki makinelerin he ? psi çalıştırılırsa bu iş kaç dakikada biter www.matematikkolay.net 1 makine bu işi t sürede bitiriyor olsun. a makine bu işi 14 saatte bitiriyorsa; 1 1 a eşitliğini kurabiliriz. t 14 a 1 t 14a dır. t 14 b makine bu işi 21 saatte bitiriy : orsa; 1 1 b t Çözüm eşitliğini kurabiliriz. 21 b 1 t 21b dir. t 21 14 2 a 21 3 b ise a 3k ve b 2k diyebiliriz. t 14a 14.3k 42k olur. a b makine çalıştırılırsa, 1 1 a b x saatte biter t x 1 1 5k 3k 2k 42k x 42k 1 x 42 x saat 5 Bunu dakikaya çevirelim. 42 5 60 12 42.12 504 dakika buluruz. 125

